В этом разделе вы найдете бесплатные примеры решений задач и лабораторных работ, выполненные с применением пакета Mathcad. Используйте данные примеры или закажите свою работу профессионалам.
Спасибо за ваши закладки и рекомендации
Решенные задания в Маткад онлайн
Задача 1. Расчетно-проектировочная работа посвящена решению типовых задач анализа, синтеза и оптимизации параметров контрольно-измерительного устройства (ИУ). Структурная схема (ж) выбрана в соответствии с индивидуальным вариантом задания (рис. 1.1, см. в файле).
1.1. Определите (двумя разными способами) коэффициент чувствительности ИУ , если коэффициенты чувствительности его звеньев известны.
Примечание: ответ нужно получить в виде формулы $K=K(k_1, k_2, k_3)$, связывающей значение общего коэффициента чувствительности ИУ с коэффициентами чувствительности его звеньев. Полученный результат используется в последующих расчетах.
Задача 2. Вычислить по формуле Симпсона определенный интеграл от функции: $f(x)=sqrt$, $a=2$, $b=32$ с шагом $h_1=(b-a)/10$ и с шагом $h_2=(b-a)/20$. Оценить абсолютную погрешность по правилу Рунге. Ответ дать с учетом поправки Рунге.
Решение математических задач в программе MathCAD
С помощью системы Mathcad определить число шагов, необходимое для достижения точности вычислений $10^$.
Задача 3. Урожай с виноградника определенной площади ежегодно позволяет получить $А=75$ декалитров молодого вина, 70% которого реализуется немедленно по цене $Р_1=9$ франков за литр. Оставшаяся часть идет в продажу через год по цене $Р_2=28$ франков за литр.
В производство вкладывается 80% процентов ежегодной выручки, что позволяет ежегодно увеличивать площади под виноградники и расширять производство. При этом на каждый вложенный франк дополнительно получается $В=0,2$ литра вина. Найти сумму выручки за каждый из 5-ти лет. Задачу решить аналитически и с помощью системы Mathcad.
Задача 4. Найдите графически отрезок изоляции корня и вычислите значение корня с точностью до 0,001 методом итераций. Все вычисления выполняйте с четырьмя знаками после запятой. $$e^+2x-6=0$$
Задача 5. Составьте таблицу значений функции $y=f(x)$ на отрезке $[a;b]$ с шагом $h$. В значениях функции сохраняйте три знака в дробной части. Вычисления проводить с тремя знаками после запятой. Используя квадратичную интерполяцию по полученной таблице, вычислите значение функции в точке $x=x^*$. Вычисления проводите двумя способами:
1) по формуле Лагранжа;
2) по формуле Ньютона.
Сделайте рисунок, на котором изобразите точки таблицы. Вычислите непосредственно значение функции $y=f(x)$ в указанной точке $x^*$ и сравните с значениями, полученными в результате интерполяции.
Задача 6. 1. Определить, какое приближение точнее, сравнив относительные погрешности.
2. Найти предельные абсолютные и относительные погрешности, если они имеют только верные цифры
а) в узком смысле
б) в широком смысле
3. Вычислить и найти предельные абсолютную и относительную погрешности результата
Программирование в Mathcad 13. Написание простейших циклов и условий. Урок 24
Задача 7. Найти в МатКад численное решение линейной краевой задачи для дифференциального уравнения второго порядка конечно-разностным методом, используя аппроксимацию производной второго порядка и шаг $h = 0.1$.
Задача 8. Лабораторная работа
1. Запустить программу Mathcad
2. Создать матрицы
3. Выполнить действия с матрицами
4. Найти ранг матрицы А
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А
6. НАйти обратную матрицу К. Найти детерминант матрицы А
Источник: www.matburo.ru
Сборник практических работ по Mathcad

Использование Mathcad в качестве суперкалькулятора. Функции и их графики. Интервальная переменная. Вычисление сумм и произведений. Численные методы решения уравнений и их систем. Решение уравнений в символьном виде.
Решений задач линейной алгебры. Вычисление пределов функций, интегрирование и дифференцирование.
Похожие разделы
- Академическая и специальная литература
- Физика
- Матметоды и моделирование в физике
- Академическая и специальная литература
- Химия и химическая промышленность
- Информационные технологии в химической промышленности
- Вычислительная химия
- Прикладная литература
- Компьютерная литература
- Matlab / Simulink
Смотрите также
Беленкевич Н.И., Романов В.Е. Прикладное программирование. Лабораторный практикум
- формат pdf
- размер 2.99 МБ
- добавлен 14 января 2011 г.
Минск — 2008 г. – 140 с. Лабораторный практикум по дисциплине Прикладное программирование для студентов специальностей Системы радиосвязи, радиовещания и телевидения, Многоканальные системы телекоммуникаций. Содержание. Лабораторная работа №1 Решение систем линейных алгебраических уравнений в численном и аналитическом виде (MATHCAD). Лабораторная работа №. Интерполирование функций. Лабораторная работа №. Аппроксимация, экстраполяция и сглаживани.
Вычислительная математика, с практическими заданиями в среде MathCAD
- формат mcd, doc
- размер 122.71 КБ
- добавлен 25 марта 2011 г.
Лабораторная №1 « Определение погрешностей при вычислении функций методом разложения их в степенной ряд »; лабораторная №2 «Решение систем линейных алгебраических уравнений методом Гаусса»; Контрольная работа «Решение нелинейных уравнений» с практическими заданиями в среде MathCAD
Латыпов И.И. Численные методы. Лабораторный практикум
- формат doc
- размер 5.19 МБ
- добавлен 26 сентября 2011 г.
В данном пособии даны темы лекционного курса «Численные методы», необходимый теоретический материал для выполнения лабораторных и контрольных работ; задания к лабораторным и контрольным работам с образцами выполнения данных заданий, требования, предъявляемые к студентам при оформлении лабораторных и контрольных работ; предложен примерный перечень тем для проведения вычислительного практикума. Учебное пособие адресовано студентам очного и заочного.
Мирошниченко Г.П., Петрашень А.Г. Численные методы
- формат pdf
- размер 1.04 МБ
- добавлен 21 декабря 2009 г.
СПб: СПбГУИТМО, 2007. — 120 с. Учебное пособие представляет собой описание лабораторных работ по различным разделам высшей математики. Пособие предназначено для студентов 2-3 курсов, обучающихся по специальности Прикладная математика и информатика. Работа может выполняться в любом математическом пакете, но для конкретности материал методически адаптирован к пакету MATHCAD. В тексте описания каждой работы содержится компьютерная программа. Лаборат.
Никулин А.М., Емельянова Н.З. Графика в системе Mathcad
- формат pdf
- размер 377.29 КБ
- добавлен 23 ноября 2009 г.
Метод. указания к выполнению лаб. работ. — М.: Российский гос. технологический ун-т им. К. Э. Циолковского, 2003. -38 с. Пакет Mathcad позволяет строить графики разных типов: графики в декартовых координатах, графики в полярных координатах, строить поверхности, строить линии уровня, картины векторных полей, трехмерные гистограммы, точечные графики. Для создания графиков в системе Mathcad имеется программный графический процессор. Основное внимани.
Охорзин В.А. Прикладная математика в системе MATHCAD
- формат djvu
- размер 2.99 МБ
- добавлен 10 августа 2010 г.
Изд.: Лань, СПб; Год: 2008; Стр. : 352; ISBN: 978-5-8114-0814-6 Учебное пособие состоит из трех разделов: «Численные методы», «Моделирование систем», «Оптимальное управление». Цель книги — представить сведения об основных численных алгоритмах, применяемых в моделировании и оптимизации, а также помочь в приобретении практических навыков в решении таких задач. Программы системы MATHCAD позволят студентам выполнять расчеты с помощью так называемы.
Сидоров Б.Н., Никулин А.М. (сост.) Методы вычисления определенного интеграла
- формат doc
- размер 89.83 КБ
- добавлен 29 декабря 2011 г.
Российский государственный технологический университет им. К.Э. Циолковского,2005, 20с Данное руководство предназначено для студентов, изучающих предмет «Численные методы» и выполняющих лабораторные работы по курсу «Информатика». В методических указаниях рассмотрен ряд методов вычисления определенного интеграла и приведены примеры решения задач на языке программирования и в среде Mathcad. Содержание Метод Решение задачи в Mathcad Решение задачи.
Сидоров Б.Н., Никулин А.М. (сост.) Методы решения нелинейного уравнения
- формат doc
- размер 76.5 КБ
- добавлен 29 декабря 2011 г.
Российский Государственный технологический Университет им. К. Э. Циолковского,1999, 8с Данное руководство предназначено для студентов, изучающих предмет «Численные методы» и выполняющих лабораторные работы по курсу «Информатика». В методических указаниях рассмотрены ряд методов нахождения корней нелинейного уравнения и приведены примеры решения задач на языке программирования и в среде Mathcad. Содержание Постановка задачи. отделение корней. Ме.
Тарасевич Ю.Ю. Численные методы на Mathcad’е
- формат doc
- размер 443.97 КБ
- добавлен 30 ноября 2011 г.
Учебное пособие. Астрахань, Астраханский гос. пед. ун-т, 2000, -70с Рассматривается на многочисленных примерах, каким образом решаются на Mathcad’e разнообразные задачи численного анализа (решение систем линейных и нелинейных уравнений, решение дифференциальных уравнений, аппроксимация функций и т. д.). Пособие не является ни учебником по численным методам, ни руководством по Mathcad’у. Предполагается, что читатель имеет представление об основных.
Тюканов А.С. Основы численных методов
- формат doc
- размер 4.05 МБ
- добавлен 17 января 2012 г.
СПб.: ГОУ ВПО Российский государственный педагогический университет им. А.И.Герцена, Кафедра прикладной математики, 2007-2009 г. — 266с. Теоретический материал: Введение. Основы теории погрешностей. Решение нелинейных уравнений. Решение систем линейных алгебраических уравнений.
Аппроксимация зависимостей. Численное дифференцирование и интегрирование. Решение обыкновенных дифференциальных уравнений. Решение дифференциальных уравнений в час.
Источник: www.studmed.ru
Решение задачи оптимизации в Mathcad
Для поиска минимального или максимального значения функции в Mathcad имеются функции:
Minimize(f, x1, x2, …xn)
Maximize(f, x1, x2, …xn)
f — функция без аргументов для максимизации и минимизации значений;
x1, x2, …xn — скалярные переменные, найденные в системе уравнений.
Записываем решение в пакете Mathcad
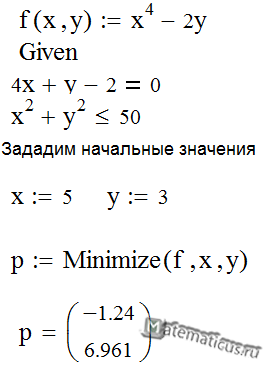

3228
Источник: www.matematicus.ru