Задачи на составление программ с циклом

Задачи на цикл while

Ниже даётся детальное объяснение самых-самых простых задач в помощь тем, кто ранее не программировал и только делает свои первые шаги в программировании. Изучив их, Вам будет намного легче перейти к более сложным задачам.

Задача №1

Необходимо, чтоб программа выводила на экран вот такую последовательность:

7 14 21 28 35 42 49 56 63 70 77 84 91 98

Решение:

public class Test <
public static void main ( String [ ] args ) <
while ( a < = 98 ) <
System . out . print ( a + » » ) ;

Комментарии к задаче:

Нам необходимо вывести вот такую последовательность чисел: 7 14 21 28 35 42 49 56 63 70 77 84 91 98

Как видите, первое число 7 и далее к каждому последующему числу прибавляется 7:

Это цикл . Данную задачу мы можем решить с помощью цикла while. Последнее число у нас 98, значит можем в цикле указать 98. Что мы и сделали с помощью вот этой строчки:

while ( a < = 98 )

Перед циклом while пишем

Решение задач на циклы в языке c++ | Практика на c++ урок 2.

Зачем мы это написали? Потому что последовательность чисел у нас начинается с 7.

А с помощью этой строчки будем выводить числа на консоль

System . out . print ( a + » » ) ;

13. Решение учебных задач на циклы

Применяя полученные навыки работы с типовыми алгоритмами, рассмотрим несколько учебных задач различных типов.

На практике нередко встречаются задачи, для которых число шагов цикла заранее неизвестно и не может быть вычислено. Как правило, в этом случае расчетный цикл работает до выполнения некоторого условия, определяющего достижение требуемого результата. Приведем пример подобной задачи.

Задана функция и ее разложение в ряд:

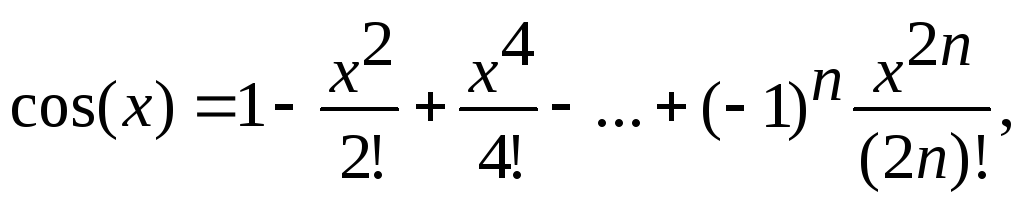
n=0, 1, 2, . (здесь n! обозначает факториал числа n, равный 1*2*3*. *n; при этом 0!=1). Найти число элементов ряда k, требуемое для достижения заданной точности ε.

Перед нами — типичная задача на ряды. С ростом величины n слагаемые 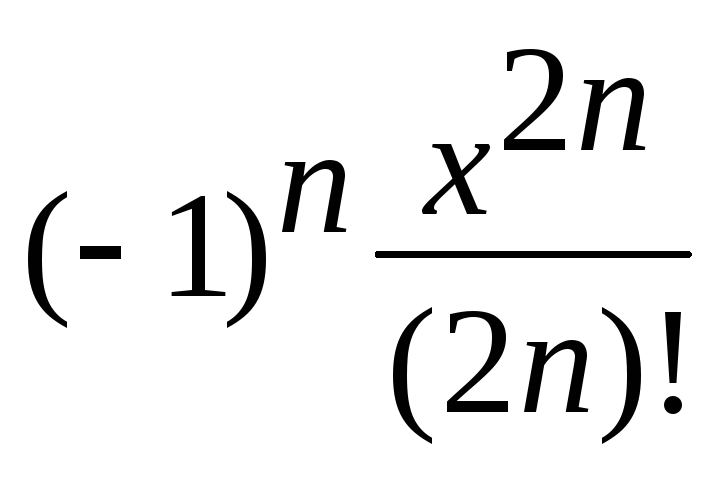становятся все меньше, равно как и модуль разности между двумя соседними слагаемыми.

Поэтому под достижением заданной точности будем понимать выполнение условия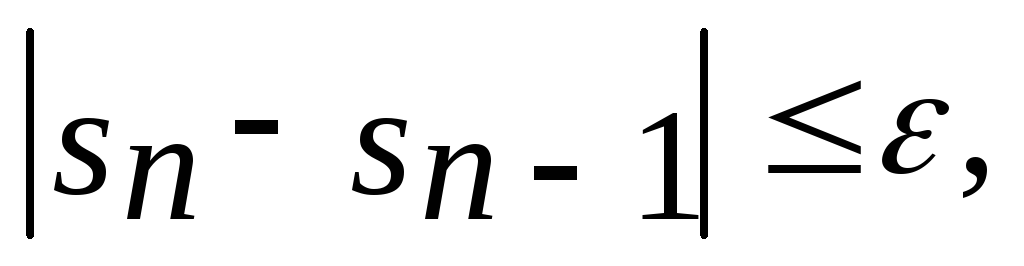гдеsn, sn-1 — суммы ряда, вычисленные на текущем и предыдущем шагах цикла, а значение ε задается малым числом, от 10 -6 и ниже. Для вычисления x 2 n введем переменную xn, которую на каждом шаге цикла будем домножать на x 2 , аналогично, для вычисления текущего значения факториала используем переменную nf. Иной подход потребовал бы большого количества повторных вычислений на каждом шаге цикла, плюс был бы чреват большими потерями точности. Для вычисления (-1) n было бы странно использовать формулу a x =e xln a — вполне достаточно завести целочисленную переменную znak, равную 1, которая на каждом шаге цикла будет менять свое значение на противоположное оператором znak:=-znak;. Кроме того, так как требуемое число шагов заранее неизвестно, используем для всех основных переменных более точный тип double вместо real.

Программирование на Python. Решаем задачи с циклом for.

Реализуем все сказанное в следующей программе:

для использования double>

writeln (‘Введите значение x:’);

writeln (‘Введите требуемую точность:’);

Источник: studfile.net