Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд.
Python. Линейные программы. Типовые задачи
На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Линейные программы, Python
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить».
В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис.
8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.

Рис. 8. Увеличение погрешности вычислений
Источник: baguzin.ru
Задачи на линейные алгоритмы
Вычислить значения выражений по формулам №№ l-26 (все переменные имеют действительный тип):

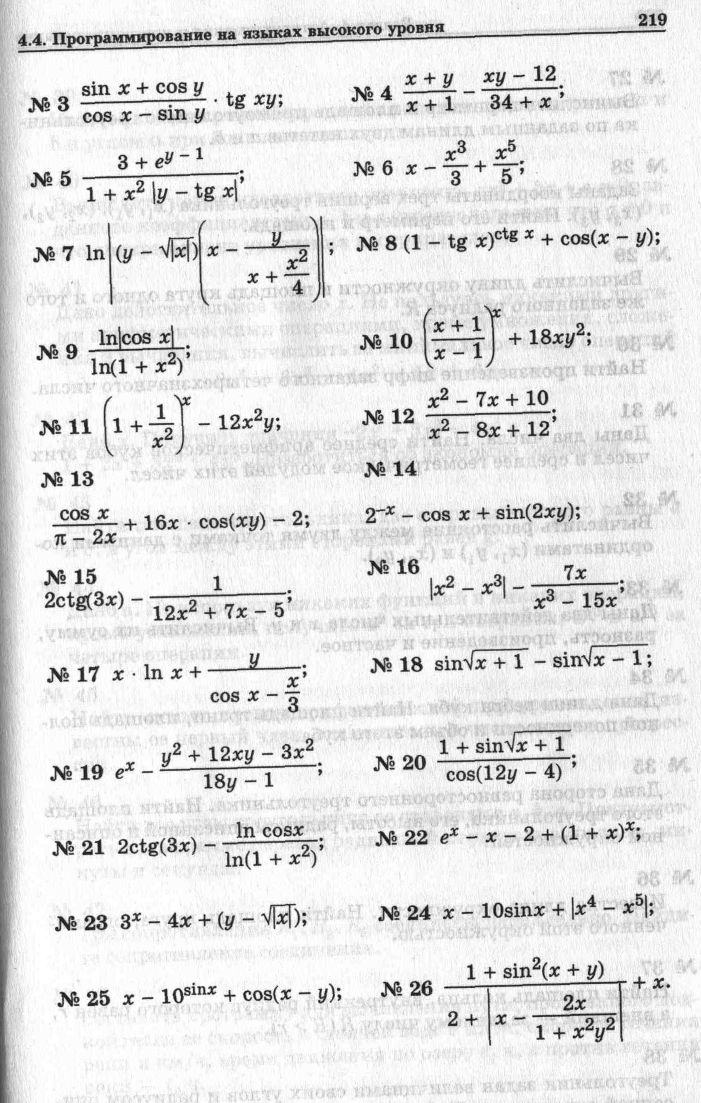
Вычислить периметр и площадь прямоугольного треугольника по заданным длинам двух катетов а и b.
Заданы координаты трех вершин треугольника (х1, y1), (х2, у2), (х3, у3). Найти его периметр и площадь.
Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.
Найти произведение цифр заданного четырехзначного числа.
Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.
Вычислить расстояние между двумя точками с данными координатами (х1, у1) и (х2, у2).
Даны два действительных числа x и у. Вычислить их сумму, разность, произведение и частное.
Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба.
Дана сторона равностороннего треугольника. Найти площадь этого треугольника, его высоты, радиусы вписанной и описанной окружностей.
Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
Найти площадь кольца, внутренний радиус которого равен r, а внешний — заданному числу R (R > r).
Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
Найти площадь равнобедренной трапеции с основаниями а и b и углом а при большем основании а.
Вычислить корни квадратного уравнения ах 2 + bx + с = 0, заданного коэффициентами a, b и с (предполагается, что а 0 и что дискриминант уравнения неотрицателен).
Дано действительное число x. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить за минимальное число операций 2x 4 — Зх 3 + 4x 2 – 5х + 6.
Дано x. Получить значения -2x + Зх 2 – 4х 3 и 1 + 2x + Зх 2 + 4х 3 . Позаботиться об экономии операций.
Найти площадь треугольника, две стороны которого равны а и b, а угол между этими сторонами равен g.
Дано а. Не используя никаких функций и никаких операций, кроме умножения, получить а 8 за три операции; а 10 и а 16 за четыре операции.
Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.
Найти все углы треугольника со сторонами a, b, с. Предусмотреть в программе перевод радианной меры угла в градусы, минуты и секунды.
Три сопротивления R1, R2, R3 соединены параллельно. Найдите сопротивление соединения.
Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде v км/ч, скорость течения реки и км/ч, время движения по озеру t1 ч, а против течения реки — t2 ч.
Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят X кошек за Y часов?
Составить программу вычисления объема цилиндра и конуса, которые имеют одинаковую высоту H и одинаковый радиус основания R.
Ввести любой символ и определить его порядковый номер, а также указать предыдущий и последующий символы.
Дана величина А, выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации.
Источник: studfile.net
ggeraldina/linear_programming_problem
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags
Nothing to show
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
- Local
- Codespaces
HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
Git stats
Files
Failed to load latest commit information.
Latest commit message
Commit time
README.md
Решение задачи линейного программирования
Номер регистрации (свидетельства): 2019666308
Название программы для ЭВМ:
Решение задачи линейного программирования
Программа, предназначенная для решения задачи линейного программирования. Функционал программы предлагает два подхода к решению задачи: 1) с помощью метода искусственного базиса; 2) с использованием заданных базисных переменных. После выбора необходимого метода пользователь вводит задачу одним из двух способов: либо загружает из файла, либо вводит данные вручную.
Решение задачи разделено на две части. В зависимости от выбранного подхода в 1 части осуществляется поиск базиса с помощью метода искусственного базиса или выражение заданных базисных переменных из ограничений задачи с помощью метода Гаусса; 2 часть — решение задачи симплекс методом.
Программа поддерживает два режима решения задачи: пошаговый, с возможностью выбора опорного элемента; автоматический. Управление параметрами программы осуществляется через главное меню. Тип ЭВМ: IBM PC-совмест. ПК; ОС: Windows 6.1 и более поздние версии.
Объем программы для ЭВМ:
Решение с помощью метода искусственного базиса

1 часть решения


2 часть решения

Решение с использованием заданных базисных переменных


About
Решение задачи линейного программирования (2017-2018г)
Источник: github.com