Wolfram mathematica примеры программ

В статье рассматриваются примеры решения обыкновенных дифференциальных уравнений в системе Wolfram Mathematica.

Ключевые слова

WOLFRAM MATHEMATICA, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Текст научной работы

Системы компьютерной математики (Maple, Mathematica, MatLab, Derive и др.) применяются в различных областях науки. Они содержат процедуры для численных и аналитических расчетов, средства программирования, визуализации. В настоящее время пакеты прикладных программ используются не только при решении численных задач, но и при доказательстве теорем.

Системы компьютерной математики используются в решении математических проблем в работах Д.С. Воронова, О.П. Гладуновой, Е.С. Корнева, М.В. Куркиной, Е.Д. Родионова, Я.В. Славолюбовой, В.В. Славского, Н.К.

Смоленцева, Л.Н. Чибриковой и др.

Система компьютерной математики Wolfram Mathematica является одним из наиболее распространенных программных средств, которое позволяет выполнять численные, символьные вычисления, имеет развитую двумерную и трехмерную графику, а также встроенный язык программирования высокого уровня. Для знакомства с языком программирования Wolfram Language рекомендуется интернет-ресурс Wolfram Language Наука», 2016. С. 105-107.

Букушева А.В. Использование систем компьютерной математики для решения геометрических задач сложного уровня // Информационные технологии в образовании: Материалы VI Всероссийской научно-практической конференции. – Саратов: ООО «Издательский центр «Наука»». 2014. – С. 76-77.

Букушева А.В. Решение учебно-исследовательских задач с использованием систем компьютерной математики // Информационные технологии в образовании: Материалы VII Всеросс. научно-практ. конф. – Саратов: ООО «Издательский центр «Наука»», 2015. С.185-187.

Букушева А.В. Учебно-исследовательские задачи в продуктивном обучении будущих бакалавров-математиков // Образовательные технологии. 2016. №2. С. 16-26.

Вельмисова А.И. Распространение и отражение гармонических волн в плоском акустическом слое с гибкими стенками в случае разрыва упругих свойств на одной из стенок // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2010. Вып.12. С. 136-140.

Вельмисова А.И., Вильде М.В., Кириллова И.В. Распространение и отражение гармонических волн в плоском акустическом слое с кусочно-неоднородными гибкими стенками // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2011. Т.11. №4. С. 68-73.

Цитировать

Зинина, А.И. Использование Wolfram Mathematica в решении дифференциальных уравнений / А.И. Зинина. — Текст : электронный // NovaInfo, 2016. — № 55. — С. 5-9. — URL: https://novainfo.ru/article/8754 (дата обращения: 03.07.2023).

Язык Wolfram Mathematica с нуля | #1 Первая программа на wolfram.

Поделиться

Настоящий ресурс содержит материалы 16+

Источник: novainfo.ru

Язык Wolfram Language ™

Освещая разнообразие областей деятельности, стилей программирования, и размеров проектов, галерея программ на языке Wolfram Language содержит различные примеры того, что можно сделать с помощью наукоемкого языка Wolfram Language, включая развертывание приложений в интернете и в других средах.

Реализация “ Hello, World ” в облаке

Создание фильтров для изображений

Интерфейс для создания логотипов

Скрытые сообщения в изображениях

Визуализация траектории солнца за год

Разработка панели мониторинга погоды

Распознавание рукописных цифр

Реализация игры “ Жизнь ”

Интерпретация естественного языка

Генерация случайных удобопроизносимых слов

Стихи или проза?

Отслеживание волка с GPS маячком

Визуализация случайного блуждания

Определить язык по фрагменту текста

Определить автора по фрагменту текста

Карта облаков вулканического пепла

Создание таблицы графов

Классификация изображений по времени суток

Генерация 3D изображения из карты возвышенностей

Карта плотности населения

Закраска стран на карте

Проверка и оценка текста

Генерация мнемокодов для телефонных номеров

Создание карты флагов

Размытие лиц на фото

Закраска стран на основе их ВВП

Сравнение современного и старого английского языка

Создание URL для определения температуры

Создание объектов поп-арта

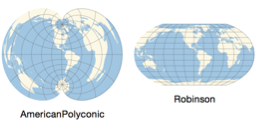
Построение центрированной карты мира

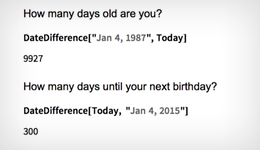
Расчет возраста в днях

Узнать численность населения страны

Генерация 3D изображения из облака точек

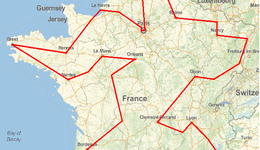
Планирование тура по городу

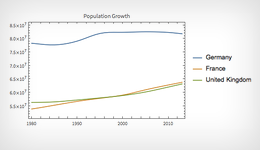
График роста населения

Создание карты возвышенностей

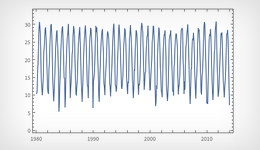
Исследование сезонных температур

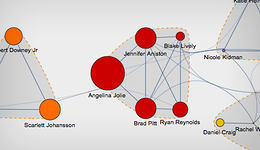
Визуализация светского обозрения

Тест на идентификацию флагов

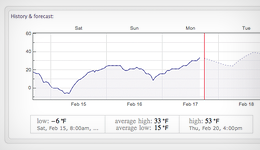
Email-предупреждение о заморозках

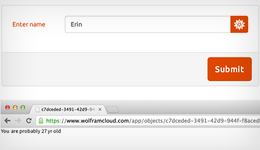
Создание сайта для определения возраста

Обнаружение лиц в реальном времени

Классификация тем на Facebook

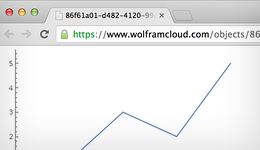
Регистрация данных в облаке

Вам также могут быть полезны:

Wolfram Demonstrations Project
Более 11 000 интерактивных демонстраций, созданных с помощью Wolfram Language

Центр документации языка Wolfram Language
Более 100 000 поясняющих примеров использования языка Wolfram Language

• Продукция
• Wolfram|One
• Mathematica
• Wolfram|Alpha Notebook Edition
• Wolfram|Alpha Pro
• Мобильные приложения
• Mobile Apps
• Finance Platform
• System Modeler
• Wolfram Player
• Wolfram Engine
• WolframScript
• Wolfram Workbench
• Корпоративные и установочные лицензии
• Enterprise Private Cloud
• Сервер приложений
• Весь список.

• Услуги
• Технический консалтинг
• Корпоративное консультирование

• Для покупателей
• Онлайн магазин
• Регистрация продукции
• Загрузка продукции
• Преимущества сервисных планов
• Портал пользователя
• Ваш аккаунт

• Поддержка
• Часто задаваемые вопросы поддержки
• Техническое сопровождение
• Обратиться в службу поддержки

• Обучение
• Документация языка Wolfram Language
• Книга: Введение в язык Wolfram Language
• Начать работу с Wolfram
• Краткое введение для программистов
• Краткое введение для изучающих математику
• Вебинары и тренинг
• Wolfram U
• Летние мероприятия
• Видео
• Книги

• Ресурсы открытого доступа
• Wolfram|Alpha
• Demonstrations Project
• Resource System
• Connected Devices Project
• Wolfram Data Drop
• Wolfram + Raspberry Pi
• Wolfram Science
• Computer-Based Math
• MathWorld
• Хакатоны
• Вычислительное мышление
• Весь список.

• Компания
• Мероприятия
• О компании Wolfram
• Вакансии
• Контактная информация

• Связь
• Сообщество Wolfram Community
• Блог Wolfram
• Бюллетень

• Правовые вопросы и Политика конфиденциальности
• Карта сайта
• WolframAlpha.com
• WolframCloud.com

Источник: www.wolfram.com

Введение в Wolfram Mathematica

2013-05-25 в 16:51, admin , рубрики: mathematica, Wolfram, математика, Программирование, метки: mathematica, Wolfram

Введение

На хабре уже не раз упоминалась Mathematica и если вам хочется начать работать с ней, то эта статья для вас. Я расскажу об основных аспектах работы с нею и покажу несколько интересных нововведений из последних версий Wolfram Mathematica.

Wolfram Mathematica — это программное обеспечение, не только для математических вычислений, это гораздо больше: от моделирования и симуляции, визуализации, документации, до создания веб-сайтов. Mathematica обладает возможностью осуществлять вызовы функций и принимать вызовы с C, .NET, Java и других языков, генерировать C код, компилировать автономные библиотеки и исполняемые файлы.
Обо всех достоинствах Wolfram Mathematica можно почитать на официальном сайте

Для начала работы с Mathematica вам необходимо её получить и установить на свой компьютер. Mathematica прекрасно работает на Windows, Mac, Linux.
Скачать и бесплатно попробовать Mathematica так же можно на оф. сайте.
Если же вы надумаете её купить, то цены на неё вполне приемлемые. Например для студента за семестровый вариант она обойдётся в $44.95. Для домашнего использования в $295. Если вы планируете использовать её для коммерческих целей, то наилучший вариант лицензии это Standard Edition (Вы получаете подписку на Premier Service и бесплатные обновления).

Все версии Mathematica абсолютно одинаковые, и отличаются только лицензированием. Все что вы можете делать в Enterprise версии, вы можете делать и в Student.

Изучение

Самая лучшая книга по Mathematica — это встроенный Help. Имеет огромную кучу туториалов и советов. Огромное множество примеров. Всё что вам может понадобится находится там. Это первое место где нужно искать нужную информацию.

Однако, если вам нужно больше, в интернете огромное множество сообществ посвещённых Mathematica. (Например: mathematica.stackexchange.com).

Блокноты и Ячейки

Все вычисления в Mathematica находятся в блокнотах. И имеют расширение .nb. В блокнотах находятся как и код, так и результаты вычислений. Блокноты разбиты на ячейки различного типа:

• Ячейки ввода – в них задаются команды, которые будут вычислены
• Ячейки результата – в них выводится результат вычислений
• Другие ячейки – ячейки с текстом, заголовки и все остальное

Нумерация ячеек идёт в том порядке в котором вы их запустили. Для того что-бы вычислить значение ячейки нажмите SHIFT+ENTER или правый ENTER, либо Evaluation -> Evaluate Cells.

Для того что-бы обратиться к значению последней вычисленной ячейке используйте знак %.

Бесконечная точность

Одной из замечательных особенностью Mathematica является концепция бесконечной точности. Если результатом вычислений является корень из двух, то она так и напишет.

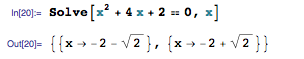
Вы можете попросить округлить ответ так:

Или же добавить дробную часть (или просто точку) к числам в выражении:

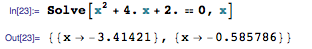
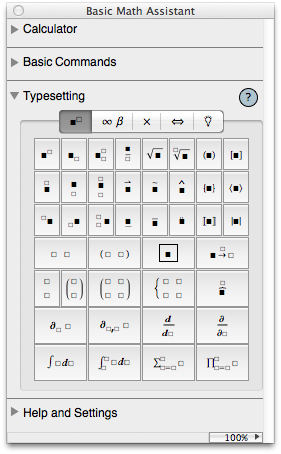
Ввод формул

В Mathematica реализован удобный ввод формул. Но для начала вам могут пригодится палитры (На картинке справа находится Palettes -> Basic Math Assistant).

У каждой кнопочки на палитре, есть свой горячие клавиши. Например, что бы написать знак интеграла нужно нажать Esc int Esc.

Вот список наиболее часто используемых горячих клавиш:

• CTRL+2 – Шаблон квадратного корня
• CTRL+6 – Верхний индекс
• CTRL+7 – Надстрочный символ
• CTRL+- – Нижний индекс
• CTRL+= – Подстрочный символ
• CTRL+/ – Дробь
• CTRL+2, затем CTRL+5 – Корень любой степени
• ALT+ENTER – Создает новую ячейку
• SHIFT+CTRL+D – Разбивает текущую ячейку
• SHIFT+CTRL+M – Склеивает несколько ячеек

Выражения, Списки, Функции

Все что записано внутри ячеек является выражениями. Каждое выражение состоит из головы и списка. Например в выражение Power[2, 2]. В нём головой является Power, а списком 2, 2.
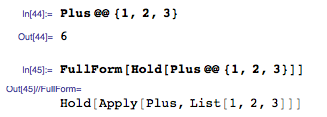
Даже 2+2 является выражением. Чтобы посмотреть как Mathematica интерпретирует ввод, есть функция FullForm:

Функция Hold просит математику не вычислять выражение. Обратной функция является Evaluate.

Списки в Mathematica создаются при помощи фигурных скобок: <. >, что является сокращением от List[. ].

Для манипуляции со списками в Mathematica есть огромная куча функций. Всё что вам может когда-нибудь понадобиться уже есть там. Вам остаётся только найти нужную функцию.

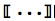
Для того чтобы получить элемент списка есть функция Part, c сокращённым вариантом в виде двойных квадратных скобок [[. ]] либо с толстыми скобками (Esc [[ Esc).

Поскольку всё является выражениями (и списки тоже), мы может получить голову выражения таким вот способом:

Таким образом чтобы индекс первого элемента в списке это 1.

А так же инфикс: из x ~ f ~ y получим f[x, y].

Однострочное программирование

В Mathematica есть множество функций для обычного программирования, такие как For, If, Switch. Однако, их лучше не использовать без крайней необходимости. Так как практически всё тоже самое можно сделать в одну строчку при помощи специальных функций и их комбинированием (поначалу бывает сложно перестроиться на такой стиль программирования).

Вот хорошее видео демонстрирующее как работают некоторые из функций:

Динамические интерактивные вычисления

Одной из замечательнейших возможностью Mathematica, являются динамические вычисления. Они позваляют манипулировать данными и смотреть на то как динамически меняется результат.

Для динамических вычислений используются функции Dynamic, Manipulate и др.

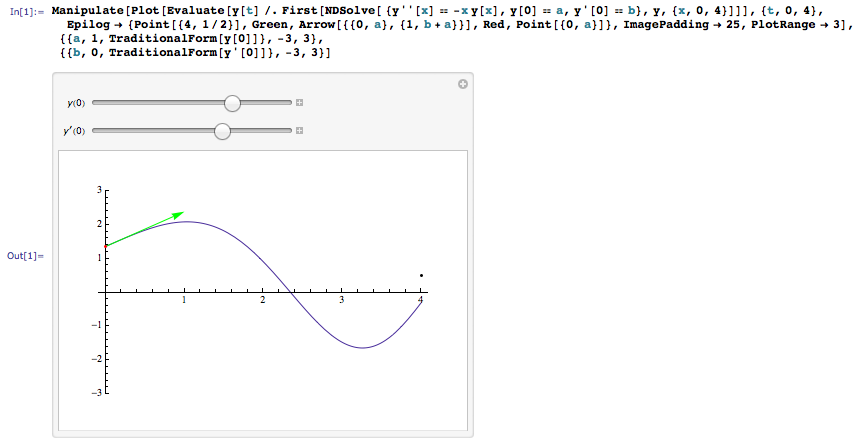
Заключение

В статье я рассказал о основных аспектах работы в Mathematica. Есть также несколько других важных моментов, таких как паттерны, модули, ядра. О них я расскажу в следующий раз, если эта тема будет интересна вам.

PS Обо всех найденных ошибках сообщайте мне в личку.

Источник: www.pvsm.ru