ГДЗ по математике 5 класс Мерзляк – это то, что необходимо каждому пятикласснику. Замечательное подспорье, которое поможет не только усвоить какую-то определённую тему, но и вообще все, проходимые в этот период обучения. Не спешите делать выводы о том, что школьник будет бездумно списывать домашнюю работу (хотя и такие машинальные действия ведут к запоминанию).
Ученик получит возможность разобраться в каком-то вопросе в спокойной домашней обстановке. И не нужно будет ехать куда-то в другой район к репетитору после школы, когда хочется просто полежать посмотреть телевизор или погулять с друзьями. Главный плюс заключается в том, что подросток сам выбирает удобное для себя время и готовиться совершенно бесплатно, но не менее эффективно. Потому что в таких ситуациях важно обеспечить полный комфорт, чтобы у ребенка не возникали отрицательные эмоции при упоминании дисциплины. С такой книгой он будет готовиться с удовольствием.
Как решебник по математике 5 класс Мерзляк сделает учебу не только полезной, но и приятной
В онлайн-решебнике собраны все развлекательные материалы специально для такого возраста. Здесь есть веселые головоломки, кроссворды, красивые картинки, приятный глазу дизайн и простой интерфейс. Это сделано для того, чтобы ученик мог разобраться во всем сам, не отвлекая от важных дел родителей, которые итак устают после работу и учителя-предметника, у которого тоже нет свободной минутки. Математика пятый класс Мерзляк обладает следующими преимуществами:
Как делить числа с остатком? Деление на двузначное число с остатком.
- одобрено федеральным государственным образовательным стандартом;
- быстрая загрузка на компьютере, ноутбуке, планшете, смартфоне, электронной книжке;
- постоянное обновление с учетом изменений в оригинальном печатном издании;
- наличие мобильной версии для телефонов с любыми операционными системами;
- не придется отправляться на поиски нужной литературы по всем книжным магазинам вашего города, всё находится под рукой.
Таким образом, в дневнике будут только пятерки, а на лице улыбка!
Ответы из решебника
Глава 1. Натуральные числа
§1. Ряд натуральных чисел
Вопросы (страница 6)
Решаем устно (страница 6)
§2. Цифры. Десятичная запись натуральных чисел
Вопросы (страница 9)
Решаем устно (страница 10)
§3. Отрезок. Длина отрезка
Вопросы (страница 19)
Решаем устно (страницы 19-20)
§4. Плоскость. Прямая. Луч
Вопросы (страница 29)
Решаем устно (страница 29)
§5. Шкала. Координатный луч
Вопросы (страница 36)
Решаем устно (страница 36)
§6. Сравнение натуральных чисел
Вопросы (страница 42)
Решаем устно (страница 42)
Проверь себя
Глава 2. Сложение и вычитание натуральных чисел
§ 7. Сложение натуральных чисел. Свойства сложения
Вопросы (страница 50)
Решаем устно (страница 51)
§8. Вычитание натуральных чисел
Вопросы (страница 56)
Решаем устно (страницы 56-57)
§9. Числовые и буквенные выражения. Формулы
Вопросы (страница 65)
Решаем устно (страница 65)
§10. Уравнение
Вопросы (страница 71)
Решаем устно (страница 71)
§11. Угол. Обозначение углов
Вопросы (страница 74)
Решаем устно (страница 75)
§12. Виды углов. Измерение углов
Вопросы (страницы 80-81)
Решаем устно (страница 81)
§13. Многоугольники. Равные фигуры
Вопросы (страница 86)
Решаем устно (страница 87)
§14. Треугольник и его виды
Вопросы (страница 92)
Решаем устно (страница 92)
§15. Прямоугольник. Ось симметрии фигуры
Вопросы (страница 98)
Решаем устно (страница 98)
Проверь себя
Глава 3. Умножение и деление натуральных чисел
§16. Умножение. Переместительное свойство умножения
Вопросы (страница 109)
Решаем устно (страница 109)
§17. Сочетательное и распределительное свойства умножения
Вопросы (страница 116)
Решаем устно (страницы 116-117)
§18. Деление
Вопросы (страница 122)
Решаем устно (страница 123)
§19. Деление с остатком
Вопросы (страница 132)
Решаем устно (страница 132)
§20. Степень числа
Вопросы (страница 136)
Решаем устно (страница 136)
§21. Площадь. Площадь прямоугольника
Вопросы (страница 141)
Решаем устно (страница 141)
§22. Прямоугольный параллелепипед. Пирамида
Вопросы (страница 149)
Решаем устно (страница 150)
§23. Объём прямоугольного параллелепипеда
Вопросы (страница 156)
Решаем устно (страница 156)
§24. Комбинаторные задачи
Вопросы (страница 163)
Решаем устно (страница 163)
Проверь себя
Глава 4. Обыкновенные дроби
§25. Понятие обыкновенной дроби
Вопросы (страница 172)
Решаем устно (страница 172)
§26. Правильные и неправильные дроби. Сравнение дробей
Вопросы (страница 183)
Решаем устно (страница 184)
§27. Сложение и вычитание дробей с одинаковыми знаменателями
Вопросы (страница 188)
Решаем устно (страница 188)
§28. Дроби и деление натуральных чисел
Вопросы (страница 192)
Решаем устно (страница 192)
§29. Смешанные числа
Вопросы (страница 197)
Решаем устно (страница 197)
Проверь себя
Глава 5. Десятичные дроби
§30. Представление о десятичных дробях
Вопросы (страница 207)
Решаем устно (страница 207)
§31. Сравнение десятичных дробей
Вопросы (страница 212)
Решаем устно (страница 213)
§32. Округление чисел. Прикидки
Вопросы (страница 218)
Решаем устно (страница 218)
§33. Сложение и вычитание десятичных дробей
Вопросы (страница 222)
Решаем устно (страница 222)
§34. Умножение десятичных дробей
Вопросы (страница 230)
Решаем устно (страница 231)
§35. Деление десятичных дробей
Вопросы (страница 240)
Решаем устно (страница 240)
§36. Среднее арифметическое. Среднее значение величины
Вопросы (страница 249)
Решаем устно (страница 249)
§37. Проценты. Нахождение процентов от числа
Вопросы (страница 254)
Решаем устно (страница 254)
§38. Нахождение числа по его процентам
Решаем устно (страница 260)
Проверь себя
Упражнения для повторения за курс 5 класса
Итоговые задания в тестовой форме. Варианты
Царица наук зачастую вызывает у школьников больше отрицательных эмоций, чем положительных. Неудивительно, ведь некоторые люди вообще считают, что она не пригодится. Такое мнение возникает потому, что взрослые вовремя не объясняют детям все значение данного предмета для жизни отдельного человека и общества в целом. Это очень плохо, так как многие исследования показали, что главнейшим условием успеха является интерес и мотивация. То есть, если учащийся будет осознавать роль, а также увидит в ней что-то увлекательное, он начнет сам изучать ее с желанием и рвением.
Как объяснить деление в столбик? Деление чисел уголком. Деление на многозначного на однозначное.
Курс математической науки представляет собой фундамент для общего образования, при том доминирующая функция — это интеллектуальное развитие. Судя по многочисленным экспериментам, становится ясно, что эта дисциплина благотворнее всех остальных влияет на работу мозга, ускоряет ее, а также тренирует память.
Весь материал основан на взвешенном соотношении новых и ранее усвоенных азов, он учитывает индивидуальные особенности каждого ребенка. А теперь к важнейшему: практическая значимость состоит в том, что объектом и предметом изучения являются пространственные формы и количественные отношения реального мира. То есть, в современном социуме эта подготовка и навыки просто обязательны каждому, так как аспекты этой области существуют во всех сферах жизнедеятельности. Ни одно открытие и изобретение не может появится без соответствующих расчетов, которые и берутся из алгебры и геометрии.
Какую пользу принесет предложенный онлайн-решебник по математике для 5 класса от Мерзляка
Создателями этого решебника выступили высококлассные методисты, поэтому информация проверенная и достоверная. Каждый раздел детально разобран и разъяснен для тех, кто не улавливает все от преподавателя. Упражнения выполнены поэтапно для того, чтобы обучающийся действительно осознал принцип выполнения примера и применял его в дальнейшем. Кратко о достоинствах издания, авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.:
- исключительно правильные решения;
- вы сможете брать его с собой и пользоваться на перемене подготавливаясь к уроку, или непосредственно на занятии;
- поиск сведений выполняется элементарно: по названию и по номеру страницы или упражнения;
- возможность почувствовать уверенность в своих собственных силах, психологический комфорт и избавиться от стрессов.
Содержание учебно-методического комплекса ответы по математике 5 класс Мерзляк
Пособие включает главы, рекомендованные в указанный период:
- Десятичная запись натуральных чисел, их ряды.
- Виды способов решения задач.
- Проценты от числа и наоборот
- Среднее арифметич., статистика, комбинаторика.
Источник: gdz.moda
ГДЗ учебник по математике 2 класс Дорофеев. Часть 2. Страница 54. Номер №4
Выполни действия.
28 − 8 − 3 ;
43 − 3 − 6 ;
83 + 5 + 12 ;
45 + 13 − 8 ;
35 + 12 + 3 ;
72 + 8 − 20 ;
80 − 5 + 14 ;
4 + 36 − 8 ;
85 + 5 − 2 .
reshalka.com
ГДЗ учебник по математике 2 класс Дорофеев. Часть 2. Страница 54. Номер №4
Решение
28 − 8 − 3 = 20 − 3 = 10 + 10 − 3 = 10 + 7 = 17 ;
43 − 3 − 6 = 40 − 6 = 30 + 10 − 6 = 30 + 4 = 34 ;
83 + 5 + 12 = 88 + 12 = 100 ;
45 + 13 − 8 = 58 − 8 = 50 ;
35 + 12 + 3 = 47 + 3 = 50 ;
72 + 8 − 20 = 80 − 20 = 60 ;
80 − 5 + 14 = 75 + 14 = 89 ;
4 + 36 − 8 = 40 − 8 = 32 ;
85 + 5 − 2 = 90 − 2 = 80 + 10 − 2 = 80 + 8 = 88 .
Источник: reshalka.com
Деление столбиком
Калькулятор деление столбиком онлайн поможет Вам быстро и правильно поделить натуральные числа. Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.
РУКОВОДСТВО
Введите в соответствующие поля натуральные числа и нажмите кнопку «Рассчитать»
ТЕОРИЯ
ДЕЛЕНИЕ
Действие деление определяют с помощью действия умножения. Например, разделить число 54 на 18 — значит найти такое число, которое при умножении на 18 дает число 54. Имеем: 18 * 3 = 54, поэтому 54 : 18 = 3.
Вообще, для натуральных чисел a, b и c равенство a : b = c верно, если верно равенство b * c = a.
Рассмотрим еще несколько примеров:
156 : 12 = 13, так как 12 * 13 = 156;
345 : 15 = 23, так как 15 * 23 = 345.
В равенство a : b = c число a называют делимым, число b — делителем, число c и запись a : b — частным.
Частное a : b показывает, во сколько раз число a больше числа b или во сколько раз число b меньше числа a.
Можно ли например, вычислить частное 12 : 0? Если предположить, что такое частное существует и равно некоторому числу c, то должно выполнять равенство 0 * c = 12, но на самом деле 0 * c = 0. Следовательно, вычислить частное 12 : 0 нельзя.
А можно ли вычислить частное 0 : 0? Пусть 0 : 0 = c. Тогда 0 * c = 0. Такое равенство справедливо при любом c. А это означает, что значением числового выражения 0 : 0 может быть любое число, то есть такое частное вычислить нельзя.
Вывод: на нуль делить нельзя.
Вместе с тем, поскольку a * 0 = 0, то для любого натурального числа a верно равенство:
0 : a = 0
Также для любого натурального числа a верны равенства:
a : a = 1
a : 1 = a
Эти равенства легко проверить с помощью умножения.
АЛГОРИТМ ДЕЛЕНИЯ СТОЛБИКОМ
Рассмотрим алгоритм деления столбиком на примере:
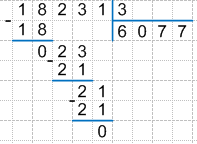
18231 : 3, где:
1. Запишем делимое и делитель с помощью уголка следующим образом:
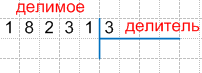
2. Определим первое неполное делимое. Для этого будем сравнивать слева направо цифры делимого с делителем, до тех пор, пока неполное делимое не станет больше делителя.
Первая цифра слева у делимого это 1. Сравним ее с делителем:
18 > 3 — значит 18 — первое неполное делимое.
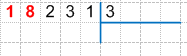
3. Разделим первое неполное делимое на делитель:
18 : 3 = 6 (остаток 0), запишем найденное частное 6 под делителем (под линией), получим:
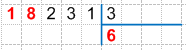
4. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
6 * 3 = 18, записываем произведение под первым неполным делимым и находим их разность, получаем:
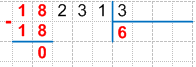
5. Сравниваем разность с делителем:
6. Определим второе неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:
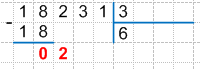
Сравним полученное число с делителем:
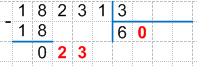
Сравним полученное число с делителем:
23 > 3, значит 23 — второе неполное делимое.
7. Разделим второе неполное делимое на делитель:
23 : 3 = 7 (остаток 2), запишем найденное неполное частное 7 под делителем (под линией), получим:
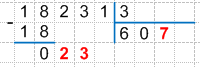
8. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
7 * 3 = 21, записываем произведение под вторым неполным делимым и находим их разность, получаем:
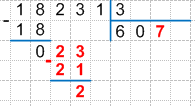
9. Сравниваем разность с делителем:
10. Определим третье неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:
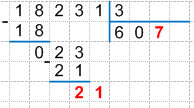
Сравним полученное число с делителем:
21 > 3, значит 21 — третье неполное делимое.
11. Разделим третье неполное делимое на делитель:
21 : 3 = 7 (остаток 0), запишем найденное частное 7 под делителем (под линией), получим:
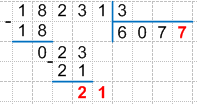
12. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
7 * 3 = 21, записываем произведение под третьим неполным делимым и находим их разность, получаем:
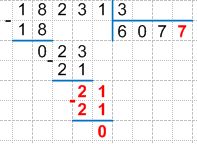
13. Сравниваем разность с делителем:
14. Так как, мы использовали все цифры делимого (сносить вниз больше нечего), значит деление завершено. Получаем:
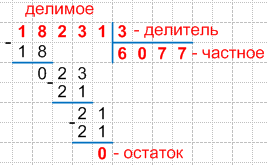
Таким образом, итоговый результат будет выглядеть следующим образом:
18231 : 3 = 6077