1. Описание проблемы
Также называемый многоугольником Тайсона или графом Дирихле, он состоит из группы непрерывных многоугольников, состоящих из вертикальных биссектрис, соединяющих две соседние линии.
2. Особенности диаграммы Вороного
(1) В каждом V полигоне есть генератор;
(2) Расстояние от точки каждого V-многоугольника до этого генератора меньше расстояния до других генераторов;
(3) Расстояние между точкой на границе многоугольника и генератором, который генерирует эту границу, равно;
(4) Граничные линии полигона Вороного смежной графики принимают исходные смежные граничные линии в качестве подмножества.
3. Применение Вороного
Важное место в дисциплине вычислительной геометрии, благодаря ее кратчайшему расстоянию от области, разделенной на набор точек, имеет широкий спектр применений в географии, метеорологии, кристаллографии, аэрокосмической, ядерной физике, робототехнике и других областях. Если вы сосредоточены на препятствиях, избегайте препятствий, чтобы найти лучший путь.
Белая Ворона и Коллектив (Психология Личности)
2. Алгоритм анализа и проектирования
Диаграммы Вороного имеют общую особенность деления смежных областей по расстоянию и имеют широкий спектр применения. Существует много методов генерации V-карт, среди которых распространены методы «разделяй и властвуй», алгоритм сканирования и алгоритм триангуляции Делоне.
1. Способ и этапы построения диаграммы Вороного
В этом эксперименте используется алгоритм триангуляции Делоне. В основном относится к генерации двухэлементной сети треугольников Делоне при генерации диаграммы Вороного, а затем найти центр описанной окружности каждого треугольника сети треугольника и, наконец, соединить центр описанной окружности соседнего треугольника, чтобы сформировать многоугольник с каждой вершиной треугольника в качестве генератора. сеть. Как показано ниже.

Ключом к построению алгоритма диаграммы Вороного является разумное соединение дискретных точек данных в треугольную сеть, то есть для построения треугольной сети Делоне.
Шаги для построения диаграммы Вороного:
(1) Дискретные точки автоматически создают сеть треугольников, то есть сеть треугольников Делоне. Пронумеруйте дискретные точки и сформированные треугольники и запишите, из каких трех отдельных точек состоит каждый треугольник.
(2) Рассчитайте центр описанной окружности каждого треугольника и запишите его.
(3) Просмотрите список треугольников, чтобы найти соседние треугольники TriA, TriB и TriC, которые совпадают с текущим треугольником pTri.
(4) Если найден, соедините внешний центр найденного треугольника с внешним центром pTri и сохраните его в списке ребер Vino. Если его не удается найти, найдите крайний перпендикулярный луч и сохраните его в списке краев Vino.
(5) После завершения обхода все ребра Вино найдены, и диаграмма Вино построена в соответствии с ребрами.
ВОРОНА: Умная и хитрая птица — Главная бандитка и санитар всех городов | Интересные факты о воронах
2. Генерация триангуляции Делоне
Ключом к построению диаграммы Вороного является генерация триангуляции Делоне. Характеристики треугольной сети Делоне:
(1) Пустой круг, любой треугольник, описанный в треугольнике, не содержит других точек.
(2) Ближайший: треугольник формируется из трех ближайших точек, и каждый отрезок линии (сторона треугольника) не пересекается.
(3) Уникальность. Независимо от того, откуда построена территория, вы получите последовательные результаты.
(4) Оптимальность: если диагональ выпуклого четырехугольника, образованного любыми двумя соседними треугольниками, взаимозаменяемы, то наименьший угол среди шести внутренних углов двух треугольников будет Получить больше.
(5) Максимальное правило. Если наименьший угол каждого треугольника в сети треугольников расположен в порядке возрастания, расположение сети треугольников Делоне получит наибольшее значение.
(6) Региональность: при добавлении, удалении или перемещении определенной вершины она влияет только на соседний треугольник.
(7) Оболочка с выпуклыми многоугольниками: внешняя граница треугольной сетки образует выпуклую многоугольную оболочку.
Подразделение Делоне является стандартом триангуляции, и существует множество алгоритмов для его реализации. На этот раз, используя алгоритм Бойера-Ватсона, основные шаги алгоритма:
(1) Создайте супер треугольник, включающий все рассеянные точки, и поместите его в список треугольников.
(2) Вставьте рассеянные точки в точку, установленную в последовательности, и найдите описанную окружность в списке треугольников.
Вставьте треугольник точки (называемый треугольником влияния точки), удалите общий край треугольника влияния и соедините точку вставки со всеми вершинами треугольника влияния, завершая точку в треугольнике Делоне. Вставьте в связанный список.
(3) Оптимизируйте вновь сформированные треугольники в соответствии с критериями оптимизации. Поместите сформированный треугольник в список треугольников Делоне.
(4) Повторяйте шаг 2 выше, пока все точки рассеяния не будут вставлены.

Ключевой шаг 2 показан ниже:
Критерии локальной оптимизации на шаге 3 относятся к:
1. Оптимизируйте вновь сформированный треугольник и объедините два треугольника с общими сторонами в один многоугольник.
2. Проверьте с помощью критерия максимального пустого круга, чтобы убедиться, что четвертая вершина находится внутри окружности треугольника.
3. Если это так, диагональ коррекции собирается измениться, то есть процесс локальной оптимизации завершен.

Процесс LOP (процедура локальной оптимизации) показан на следующем рисунке:
3. Проектирование структуры данных
В реализации этой программы используется объектно-ориентированный язык C #, поэтому структура структуры данных принимает форму класса, а именно:
Точка: public class Site < public double x, y; public Site() < >public Site(double x, double y) < this.x = x; this.y = y; >> Край: public class Edge < public Site a, b; public Edge(Site a, Site b) < this.a = a; this.b = b; >> Треугольник: public class DelaunayTriangle < Voronoi voronoi = new Voronoi(); Публичный сайт site1, site2, site3; // Треугольник три точки public Site centerPoint; // Внешний круг центр public double radius; // радиус окружности public List adjoinTriangle; // Смежный треугольник public DelaunayTriangle(Site site1,Site site2,Site site3) < centerPoint = new Site(); this.site1 = site1; this.site2 = site2; this.site3 = site3; // Построить центр и радиус описанной окружности voronoi.circle_center(centerPoint, site1, site2,site3,ref radius); >>
4. Анализ сложности алгоритма
Сложность времени:
Временная сложность генерации триангуляции Делоне:
Шаг 1. Построить супер треугольник, O (1);
Шаг 2. Создайте затронутые треугольники и создайте новые треугольники, O (1 + 2 + . + n) = O (n2) O (1 + 2 + . + n) = O (n2)
Шаг 3. Выполните локальную оптимизацию вновь сформированного треугольника: O (n).
Следовательно, общая временная сложность составляет: O (1) + O (n2) + O (n) = O (n2) O (1) + O (n2) + O (n ) = O (n2).
Временная сложность генерации диаграмм Вороного из триангуляции Делоне:
Шаг 1. Построить треугольную сеть Делоне, O (n2) O (n2);
Шаг 2. Рассчитайте центр описанного треугольника O (n);
Шаг 3. Найдите соседний треугольник с трех сторон треугольника: 3O (n);
Шаг 4. Найдите ребро Vino в связанном списке и нарисуйте график Vino: O (n).
Следовательно, общая временная сложность составляет O (n2) + O (n) + 3O (n) + O (n) = O (n2) O (n2) + O (n) + 3O (n) + O (n) = O (n2).
3. Экспериментальные результаты
Случайно сгенерированные точки:

Создать сеть треугольников Делоне:

Создать диаграмму Вороного:

См. Исполняемую программу и файл проекта исходного кода для генерации диаграммы Вороного.here。
Ниже приведено объявление связанных функций (подробный код см. В файле проекта исходного кода).
// Построить треугольную сеть Делоне в соответствии с набором точек public void setDelaunayTriangle(List allTriangle, List sites); // Построим ребра диаграммы Вороного по сети треугольников Делоне public List returnVoronoiEdgesFromDelaunayTriangles(List allTriangle, List voronoiRayEdgeList); // Возвращаем все стороны треугольника в соответствии со списком треугольников public List returnEdgesofTriangleList(List allTriangle); // Частичная оптимизация новообразованного треугольника public List LOP(List newTriList); // Определяем, принадлежит ли край треугольнику public bool isEdgeOnTriangle(DelaunayTriangle triangel,Edge edge); // Определяем, принадлежит ли точка треугольнику public bool isPointOnTriangle(DelaunayTriangle triangle, Site site); // Соединяем точки с тремя точками затронутого треугольника, чтобы сформировать новые три треугольника и добавить их в цепочку треугольников public void addNewDelaunayTriangle(List allTriangles,DelaunayTriangle influenedTri,Site point); // Находим общую сторону затронутого треугольника public List findCommonEdges(List influenedTriangles); // Находим общую сторону двух треугольников public Edge findCommonEdge(DelaunayTriangle chgTri1, DelaunayTriangle chgTri2); // Определяем, находится ли точка вставки на стороне треугольника public Site[] isOnEdges(DelaunayTriangle triangle,Site site); // Определяем, находится ли точка внутри описанной окружности треугольника public bool isInCircle(DelaunayTriangle triangle, Site site) ; // Найти центр окружности треугольника public void circle_center(Site center, Site sites0, Site sites1, Site sites2, ref double radius) ; // Находим расстояние между двумя точками public double distance2Point(Site p,Site p2);
PS: из-за ограниченного времени и уровня, сообщение в блоге неизбежно будет иметь недостатки или даже ошибки. Это только для справки, и критика и исправление приветствуются.
Источник: russianblogs.com
Что такое шаблон Вороного и как сделать его с помощью 3D-принтера

Один из лидеров в технологии DVR для просмотра и записи ТВ по вашему графику, узнайте, является ли TiVo хорошим выбором для вас.
Что такое виртуальная локальная сеть (VLAN) и что она может сделать?

Узнайте, как настроить виртуальную локальную сеть (VLAN) и как VLAN позволяет настроить логические сети, имеющие устройства, разделенные по физическим подсетям.
Сделать простые графические интерфейсы с помощью малины Pi с помощью EasyGUI

Как сделать быстрые и простые графические пользовательские интерфейсы (GUI) с помощью малины Pi с помощью EasyGUI. Создавайте свои собственные графические интерфейсы быстро и легко.
Источник: ru.go-travels.com
Ход «Voronoi»
На написание статьи вдохновила игра «Wesnoth» — пошаговая стратегия с элементами RPG. В этой игре персонажи перемещаются по карте, состоящей из шестиугольных полигонов. Таким образом, окруженный со всех сторон персонаж может быть атакован шестью вражескими. По этой причине тактическая составляющая в игре очень важна. Возник вопрос: как повлияет на игровой процесс переход от карты с фиксированной геометрией полигонов на карту с произвольной геометрией?
В данном посте решил написать о возможности использования «диаграммы Вороного» в качестве случайной игровой карты. Описаний алгоритмов для построения диаграммы Вороного в сети нашел несколько. Но все, что довелось прочитать мне, либо слишком поверхностны, либо написаны академическим языком. В общем, описания, пригодного для немедленной реализации алгоритма я не нашел.
Пришлось начинать реализацию не имея четкого понимания всех тонкостей алгоритма. Нашел в сети исходники на разных языках, но для перевода на нужный мне язык и адаптации под мою задачу все равно не хватало знаний. Поэтому решился изобретать велосипед «с чуть более круглыми колесами и с седушкой помягше».
Возможно кто-то из читателей встречал описание подобной задачи с исходными кодами. Тогда оставьте, пожалуста, в комментариях ссылку — сравним с тем, что получилось у меня.
Алгоритм
Итак… серия «на пальцах» продолжается. Вы можете почитать по-русски про диаграмму Вороного в википедии [1]. Суть такова, что для случайного набора точек (центров) на плоскости (я для простоты рассматриваю 2D-случай) эта диаграмма представляет собой совокупность таких полигонов, что все точки внутри полигона находятся ближе к его «центру», чем к «центрам» других полигонов. Соответственно, все точки на границе между двумя полигонами располагаются на одинаковых расстояниях от обоих центров, а вершины полигонов равноудалены сразу от трех или даже более центров.
Самым «простым» способом построения диаграммы является построение «серединных перпендикуляров» между всеми центрами, т.е. перпендикуляров к отрезкам, соединяющим пары центров, размещенных в середине этих отрезков. Затем нужно найти точки пересечения полученных перпендикуляров и произвести отсечения. Однако вычислений при это нужно будет сделать больше всего (O(n^2 * log n)).
Есть алгоритм т.н. «заметающей прямой» (sweep line, fortune’s algorithm [2]). Его вычислительная сложность O(nlogn). Он и будет описан ниже.
Суть алгоритма
В основе этого алгоритма лежит применение вспомогательного объекта — заметающей прямой (ЗП). Она может быть вертикальной или горизонтальной. Я использую горизонтальную ЗМ, движущуюся от бОльших значений Y к меньшим.
Суть в том, что при каждом положении ЗП рассматриваются лишь точки выше этой линии и непосредственно на ней. При этом для каждого из «центрОв» строится парабола, точки на которой равноудалены от «центра» и от ЗП. В данном случае «центры» являются фокусами соответствующих им парабол, а ЗП — директриса этих же парабол.
Уравнение параболы имеет вид:
y = ((x — xf)^2 +yf^2 — L^2)/(2*(yf — L))
где xf, yf — координаты фокуса параболы (центр полигона Вороного);
L — положение ЗП (координата Y текущего обрабатываемого события).
Если построить огибающую снизу всех парабол, то получится т.н. «береговая линия» (beach line). Эта кусочная кривая играет ключевую роль в алгоритме. Точки пересечения «кусков парабол» (назовем их брейкпоинтами) лежат на границах полигонов диаграммы. Когда сходятся в одну точку два брейкпоинта, то одна из «арок» (кусок одной из парабол) «схлопывается», т.е. две соседние к ней арки соединяются друг с другом. При этом образуется вершина полигона диаграммы.
Таким образом, задача сводится к детектированию и обработке двух событий — добавления в список рассматриваемых центров новой точки (site event) и подозрение на наличие вершины (circle event) [3]. И так далее… примерно такое описалово я и находил в сети на разных языках. И на данном, концептуальном, уровне все выглядет не очень сложно. Но как именно (по шагам) осуществляется детектирование? И что именно делать с этими событиями?
Попробую изложить простыми словами.
Структура данных

Как было сказано выше, в алгоритме ключевыми объектами являются события: событие точки (site event) и событие круга (circle event). Эти события помещаются в список, который сортируется в моем случае по убыванию координаты Y, т.е. события имеющие бОльшие значения координаты Y размещаются выше в очереди и обрабатываются раньше. Таким образом, первое, что нам понадобится — упорядоченный список для хранения событий.
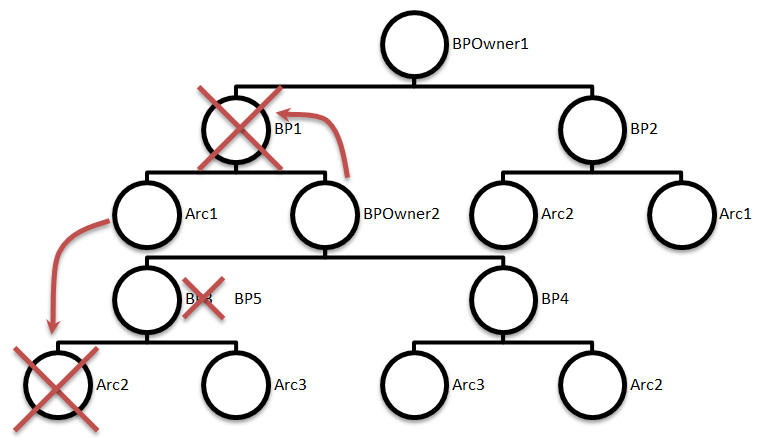
Второе, что нам понадобится — бинарное дерево. В этом дереве будут размещены узлы трех типов: Arc — арка (часть параболы), этот узел должен хранить координаты фокуса параболы и ссылку на событие круга, если таковое имеется; BP — breakpoint, точка пересечения двух парабол; BPOwner — корень поддерева, его детьми являются узлы типа BP. Узлы BP и BPOwner должны хранить ссылку на грань. Нужно обязательно хранить грани в отдельном списке, т.к. узлы BP и BPOwner будут удаляться при обработке событий круга.
Соответствие узлам Arc и BP вы легко найдете в публикации [6]. BPOwner прямого наименования не имеет — просто корень поддерева. Я дал ему наименование лишь для удобства программной реализации.
Типичная схема бинарного дерева для диаграммы Вороного (как я ее себе представляю) изображена на рис. 1.
Рис. 1. Бинарное дерево.
На этом рисунке сразу можно выделить потенциально имеющееся событие круга. Если смотреть слева, то Arc1, Arc2, Arc3 образуют тройку фокусов, которые с большой вероятностью не будут лежать на одной прямой. Больше событию круга возникнуть негде, т.к. остаются тройки , и . Такая схема построения дерева пусть и избыточна, но проста в анализе.
Подробнее структуру данных можно изучить в [6]. Возможно мое изложение отличается от представленного в той публикации, но для меня так проще.
Главный цикл
- Инициализация данных.
- Пока очередь НЕ ПУСТА:
- Вырезать из очереди первое событие (с наибольшим значением координаты Y)
- If(event = = Site Event)
ProcessSite(event) - Else
ProcessCircle(event)
Обработка «события точки»
Что такое событие точки для нашего бинарного дерева? Когда ЗП попадает на очередную точку, то в дерево добавляется новая парабола. Нужно заметить, что, во-первых, по алгоритму ЗП перемещается от события к событию (в демо-анимациях к алгоритму эта прямая движется плавно), а во-вторых, изначально парабола представляет собой вертикально направленный луч.
В месте пересечения этого луча с одной из парабол образуется сразу два «брейкпоинта» (BP). Таким образом, для каждого события точки в дереве находится парабола с которой произойдет пересечение соответствующего луча. Сделать это легко методом спуска, начиная с корня всего дерева и сравнивая координаты X этого события и узлов BPOwner и BP.
Спуск происходит до тех пор пока не встретится арка. Если арка содержит ссылку на существующее в очереди событие круга, то нужно удалить это событие из очереди и удалить ссылки на это событие из данной арки и ее соседей, арки справа и слева. Далее вместо арки (см. Arc1 ниже) создается поддерево вида:
BPOwner / BP BP / / Arc1 Arc2 Arc2 Arc1
Теперь, когда структура дерева поменялась, следует пробежать по дереву слева направо в поисках событий круга. Для этого нужно брать последовательно тройки арок и проверять координаты фокусов соответствующих им парабол на колинеарность. Если три фокуса не лежат на одной прямой, то можно построить общую для них окружность. Если нижняя точка этой окружности лежит ниже ЗП, то можно добавить в очередь событие круга. Нижняя точка окружности — это место, где событие произойдет, а центр — это точка, где будет находиться вершина полигона Вороного.
Подводя итог скажу, что события точек только добавляют узлы в дерево и события круга в очередь событий. Больше ничего при их возникновении не делается. При наступлении события точки даже не производится вычисление координат BP — точек пересечения парабол. «Главная магия» делается в обработчике событий круга.
Обработка «события круга»
Каждое событие круга должно содержать ссылку на арку, которая будет удалена («схлопнется», см. выше) при наступлении этого события. Ранее было написано, что для детектирования события круга рассматриваются тройки арок.
Так вот, в событии круга должна храниться ссылка на среднюю арку, т.е. на ту, у которой значение координаты X находится между соответствующими значениями двух других арок. В этих соседних арках также должна храниться ссылка на то же событие круга, что и у средней. Хотя особой необходимости я в этом не вижу. Мне, как «на-палечнику», проще записать в среднюю арку ссылки на две соседние арки — левую и правую. Благодаря этому не придется прогуливаться по дереву в поисках соседней ветки с нужной аркой (обязательно одна из оставшихся двух арок будет в соседней ветке, т.к. дерево бинарное).
Обработка события круга будет заключаться в обновлении координат брейкпоинтов, непосредственно ограничивающих удаляемую арку. Далее производится удаление арки и двух, связанных с ней брейкпоинтов. После этого нужно перестроить дерево. В результате будет добавлен новый узел BP, а получившееся поддерево переместится на уровень выше…
Текстом такие процедуры воспринимаются достаточно трудно. Во всяком случае для меня, как человека без серьезных знаний в теории графов и бинарных деревьев, это было нетривиальной задачей, поэтому привожу еще и иллюстрацию на рис. 2.
Рис. 2 Обработка события круга
Результат
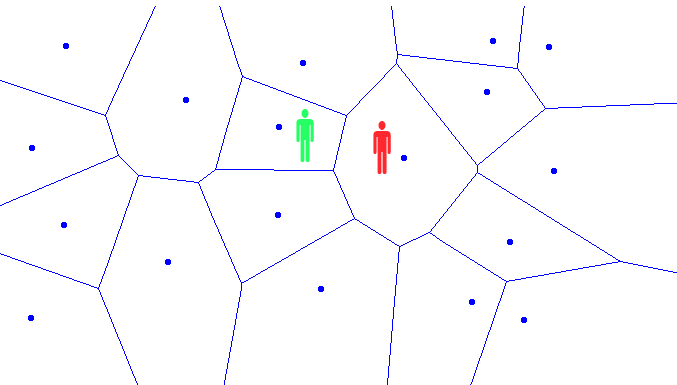
Здесь я приведу характерный вид диаграммы, т.е. вид игровой карты с произвольной полигональной геометрией.
Рис.3 Игровая карта
На этой карте в «центрАх» (напомню — это исходный набор случайно распределенных по площади точек) могут находиться персонажи. Через грани этих полигонов на персонажа может напасть персонаж противника. На представленном выше рисунке «зеленый человечик» обозначает… нет не алкоголизм.
Полигон, в котором размещен силуэт зеленого цвета — безопасная локация с точки зрения количества возможнах атак за ход противника (4 максимум). А вот персонажу красного цвета не повезло. На него может быть совершено максимум 8 нападений со стороны недружественного населения.
Тактика
Каждому полигону на карте можно присвоить «стоимость прохождения». Можно поступить иначе — назначить «стоимость пересечения» границам полигонов или использовать комбинацию того и другого (стоимость пересечения границы + половина стоимости прохождения).
Также, в зависимости от площади полигона (или количества охвачиваемых точек координатной сетки карты), можно назначить различные бонусы (периодичность рождения артефактов, происхождения каких-либо событий и пр.), очки защиты, ресурсы постройки укреплений и т.д. Это уже предоставляет большие тактические возможности.
Плюс к этому следует правильно выбирать полигон, в котором можно остановиться. Как написано в начале, большой полигон может иметь большее количество границ, а значит и большее число нападений за один ход противника. Однако большой полигон — это большие бонусы (при условии назначения бонусов в зависимости от площади, а не от количества границ).
Значит особо ценными будут полигоны с максимальной площадью при минимальном количестве границ. Вот такая задача «МаксиМин», которую нетрудно автоматизировать. Труднее автоматизировать успешное использование получаемых бонусов для ИИ.
Поиск пути можно осуществлять с использованием A* («TODO» для отдельного поста). Можно ввести систему прокладки путей — сначала проводится персонаж вручную, делается запись пути, а потом можно использовать созданные «waypoint’ы» для автоматизации. Но это будет скорее всего слишком неудобно. На геймплее может сказаться негативно.
Теперь об укреплениях. У каждого полигона должен быть некий набор ресурсов для создания укреплений, от которых будет зависеть тип фортификации и скорость возведения сооружений. Прямо «Цивилизация» получается. На укрепление в выбранной позиции персонаж тратит очки действий. Их можно разделить на две группы — защитные и атакующие.
При этом зашитные ОД тратятся на постройку укреплений и оборонительную активность во время атаки противника (поднять щит, увернуться от стрелы, блокировать атаку и пр.), а атакующие могут быть потрачены как в стадии атаки, так и при защите (контратака, обезоруживание). Тут можно упомянуть ZPG «MyBrute», в которой аватарчик может при защите перехватить инициативы и атаковать в ответ, не получив удара от противника.
Каждый персонаж может иметь набор укреплений, постройке которых он обучен. Каждый тип укреплений дает разную степень защищенности и/или бонусы. Помимо бонусов от укреплений, сам полигон может давать случайные бонусы. Пребывая долгое время в данном месте, персонаж увеличивает вероятность найти что-то ценное или «открыть» некое скрытое свойство данного полигона.
Можно и дальше продолжать такие рассуждения. Пространства для маневров предостаточно, но тогда мы отклонимся от темы статьи.
Выводы
Смена геометрии игровой карты неминуемо приведет к серьезным изменениям (думаю в лучшую сторону) в тактике игры. Появится дополнительный тактический уровень, возможность при правильном подходе в переломный момент битвы перевесить чашу весов в свою сторону. К тому же, такой подход позволит сделать игровую карту динамической — видоизменять ее топологию (локально или глобально).
Тут нельзя не вспомнить не реализованную до конца (на мой взгляд) задумку изменяемых локаций в играх «S.T.A.L.K.E.R.». В 2D это реализовать не очень сложно. Но не забываем о том, что диаграмма Вороного строится и для 3D.
Спасибо за внимание! Ваши комментарии…
Список литературы
- Диаграмма Вороного
- Voronoi Diagrams and a Day at the Beach
- Planar Voronoi Diagrams via Fortune’s Algorithm
- Polygonal Map Generation
- Voronoi diagrams
- Fortune Sweep Algorithm
Источник: habr.com
Как сделать узор Вороного с помощью 3D-принтера

Когда вы увлекаетесь 3D-печатью , вы, так сказать, возвращаетесь в школу. Кто-то отправляет вам 3D-модель, но она нуждается в некоторых изменениях или полировке, и вы открываете какое-то программное обеспечение для 3D-дизайна.
Что такое шаблон Вороного?
Вы слышите, как люди говорят о взаимосвязанных треугольниках, о сетчатых моделях, о моделях NURBS и делают модель «водонепроницаемой», прежде чем пытаться ее напечатать. Каждое хобби или жизненный путь требует времени, чтобы изучить основы и тонкости. Затем вы видите, как кто-то делает что-то действительно творческое с 3D-моделью, превращая ее в шаблон Вороного. А?
Мы нашли эту маленькую белку на Thingiverse, и она напомнила нам собаку в анимации Up!, Поэтому мы загрузили ее для печати. Как вы можете видеть, он имеет необычный дизайн — эти швейцарские сырные дыры известны как узоры Вороного. Изображение , показанное от программы слайсер Cura, но оригинальный Белок Вороного-Style на Thingiverse , по римской Hegglin , так что вы можете скачать его самостоятельно. Роман — очень активный дизайнер и имеет множество потрясающих 3D-моделей, которыми он делится с другими. Нам нравится его работа.

После 3D-печати белки на очень надежном LulzBot Mini (подразделение, предоставляющем медиа-ссуды), мы решили поискать больше об этих проектах. Как и многие энтузиасты 3D-печати , мы просто загрузили модель из Thingiverse, не задумываясь о том, как это сделать сами. Естественно, мы столкнулись с нашим приятелем, Маршаллом Пеком, из ProtoBuilds , который, как помнят читатели, — тот, кто рассказывал , как создать свой первый 3D-принтер легче, чем когда-либо .
Маршалл объясняет тонну в своем блоге, а также на Instructables, в комплекте со скриншотами, так что вы захотите отправиться туда, чтобы проверить это: Как создавать узоры Вороного с помощью Autodesk® Meshmixer .
Эти шаблоны могут обеспечить равномерное горизонтальное сечение срезов, что может быть полезно при использовании 3D-принтеров SLA / смолы. Модели Voronoi могут хорошо печатать на большинстве 3D-принтеров Fused Filament. Как уже упоминалось, мы попробовали это на LulzBot Mini.
Наш первый выход, не по вине принтера, оставил нас с полуголой белкой. На втором этапе мы позволили Cura создать для нас поддержку, что было хорошо и плохо. В нем используется тонна материала, а затем вам нужно разбить его, разрезать его, расплавить все с вашей окончательной 3D-печати. Мы определенно создаем пост «Советы по удалению структур поддержки 3D-печати».
Источник: gadgetshelp.com
Вороной по-быстрому. Сухая инструкция.
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Недавно занялся изучением программы Meshmixer, и вот первые плоды. Сухая мейкерская инструкция по созданию моделей в так называемом стиле Вороного (хотя это не стиль, а математический алгоритм).
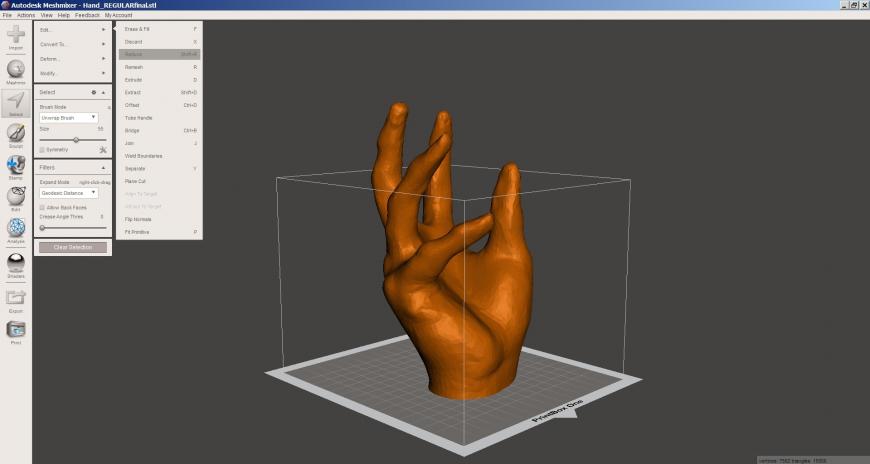
Импортируем исходную модель:

Выделяем модель (Ctrl+a). Переходим Select — Edit — Reduce
В Reduce Target выбираем Triangle Budget
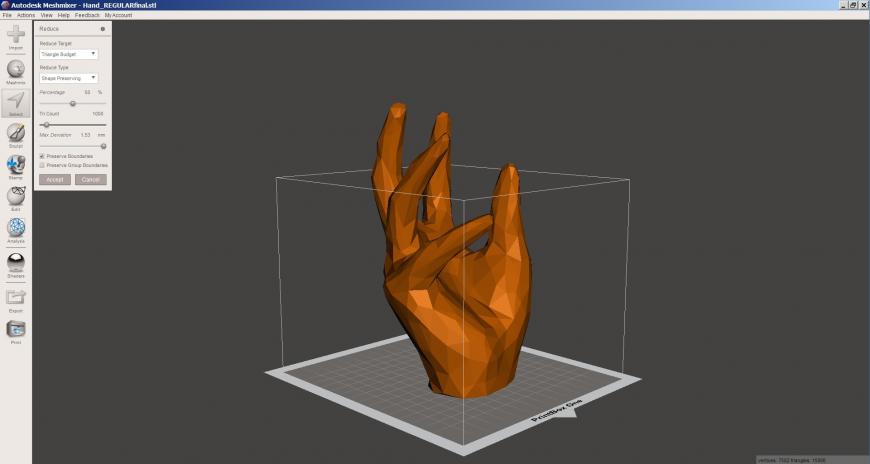
Ползунком Tri Count делаем модель низкополигональной. Чем меньше полигонов, тем крупнее будут ячейки эффекта.
Переходим в меню Edit (которое слева, а не в подменю Select).
Make Pattern. В выпадающем меню Pattern Type выбираем Dual Edges (можно также поэкспериментировать с Edges, Mesh+Delaunay Edges и Mesh+Delaunay Dual Edges).
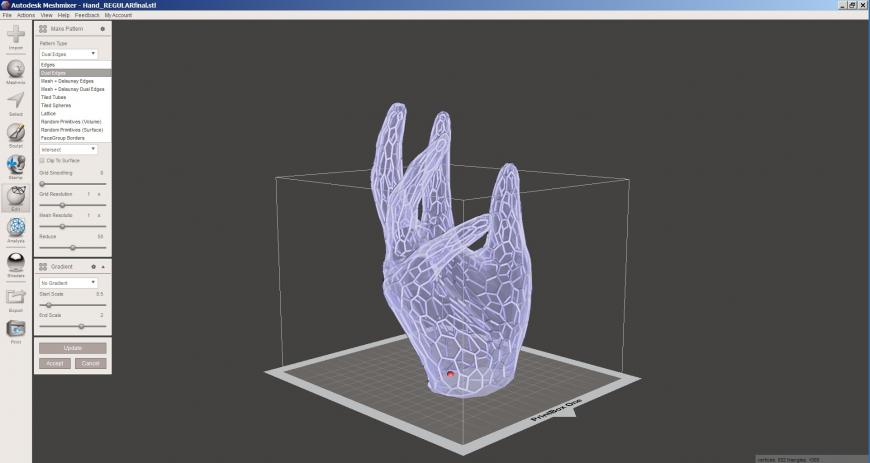
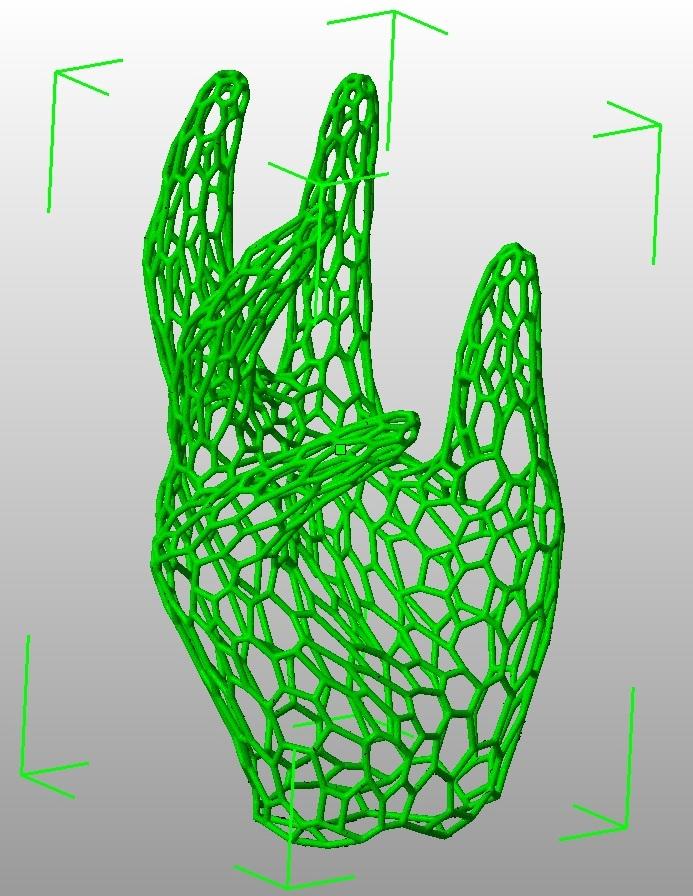
Нажимаем Accept и ждем. Процесс может быть долгим.

Сохраняем в stl: File -> Export
Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Источник: 3dtoday.ru