В программе logism построить логическую схему и таблицу истинности функции

Цель работы: изучение логических элементов компьютера и их таблиц истинности, а также построение триггеров в программе Logisim.

1. Изучена теоретическая часть.

2. Составлена логическая схема для высказывания в программе Logisim. На рисунке 1 представлена схема для данного высказывания.

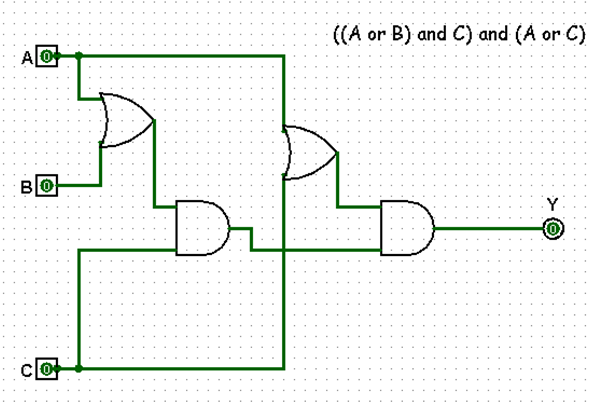
Рисунок 1. Логическая схема

3. Указывая значения A, B, C, а также получаемое значение Y на выходе, применяя программу Logisim, заполнили таблицу истинности, представленную на рисунке 2.

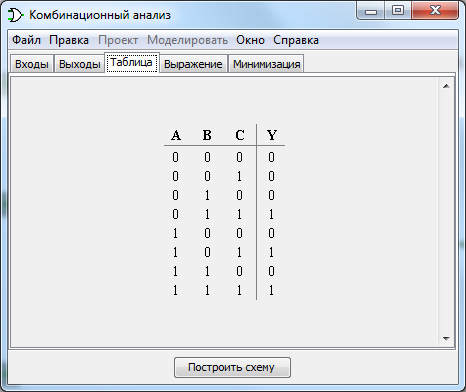
Рисунок 2. Таблица истинности

4. Составлена схема асинхронного RS-триггера на основе элементов: 2шт «И-НЕ». Схема приведена на рисунке 3. Удостоверились в возможности хранения бита информации. Составили таблицу истинности, приведенную на рисунке 4.

Построение логических схем

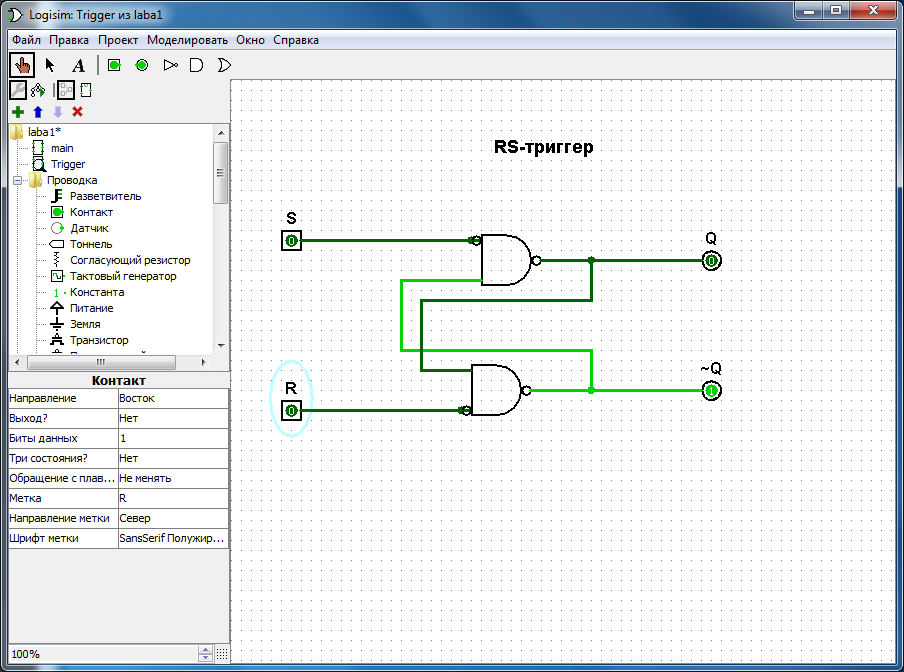
Рисунок 3. Логическая схема RS-триггера

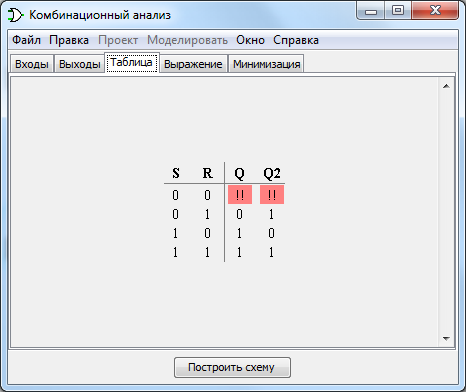
Рисунок 4. Логическая схема RS-триггера

5. При наличии двух входных сигналов, возможны 4 варианты работы схемы (Рисунок 4).

Если на вход S подать напряжение, уровень которого будет соответствовать единице, при R = 0, то выход Q скачкообразно изменит свое значение на 1, а Q^ на 0. Произойдет запись информации. Таким образом происходит установка триггера – его переключение в единичное состояние.

При подаче положительного сигнала на вход R, при S = 0, инверсный выход станет равен 1, а прямой Q = 0. Это произойдет запись информации. Триггер сброшен — то есть пришел в устойчивое нулевое состояние. Если убрать единицу с «Reset», тогда выходы не изменят свое состояние, останутся такими, какими были – проявление свойства памяти.

В нулевой момент времени, когда на оба входа (R и S) подана логическая единица, прямой выход Q = 1, но инверсный Q^ = 1 тоже, что является недопустимым. Триггер должен быть либо в устойчивом состоянии логического 0 (Q = 0 и Q^ = 1), либо в устойчивом состоянии логической 1 (Q = 1 и Q^ = 0).

Одновременное задание S = 0, R = 0 вызовет возбуждение цепи. Оба элемента начнут переключаться и с вероятностью 50/50 в единичном состоянии может оказаться любой из них

Хранение бита информации происходит следующим образом. Допустим, ранее триггер был установлен, то есть Q = 1 и Q^ = 0. Тогда решающий сигнал Q^ = 0 будет через положительную обратную связь подан на верхний элемент И-НЕ и состояние Q = 1 будет подтверждено. На входы нижнего элемента И-НЕ будет подано сочетание сигналов R = 0 и Q = 1, поэтому состояние прямого выхода триггера Q^ = 0 будет подтверждено.

Если же триггер был сброшен, то есть было Q = 0 и Q^ = 1, тогда решающий сигнал Q = 0 будет через положительную обратную связь подан на нижний элемент И-НЕ и состояние Q^ = 1 будет подтверждено. На входы верхнего элемента И-НЕ будет подано сочетание сигналов S = 0 и Q^ = 0. Таким образом, триггер хранит ранее записанную информацию.

Логические выражения, таблицы истинности ,структурная логическая схема

Вывод: в ходе данной лабораторной работы были изучены логические элементы компьютера и их таблицы истинности, а также были получены навыки в построении триггеров в программе Logisim.

Ответы на контрольные вопросы:

1. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинного оно или ложно.
2. С логическими высказываниями можно производить следующие операции:

1. Операция отрицания (НЕ).
2. Операция конъюнкции (И).
3. Операция дизъюнкции (ИЛИ).
4. Операция импликации (ЕСЛИ…ТО).
5. Операция эквиваленции (ТОГДА, И ТОЛЬКО ТОГДА).

Структурные схемы логических элементов компьютера

Структурная схема (отечественное обозначение)

Источник: studfile.net

ЛБ по Logisim. Лабораторная работа 3 Цифровая логика компьютера

Единственный в мире Музей Смайликов

Самая яркая достопримечательность Крыма

Скачать 0.57 Mb.

Лабораторная работа № 3
Цифровая логика компьютера.
1. Цель работы
Целью работы является изучение логических элементов компь- ютера и их таблиц истинности, а также построение триггеров в про- грамме Logisim.
2. Задачи работы
– Закрепление, углубление и расширение знаний студентов о ло- гических элементах компьютера.
– Приобретение умений и навыков построения триггеров в про- грамме Logisim.
– Выработка способности логического мышления, осмысления полученных результатов при построении триггеров.
3. Теоретическая часть
Любая информация в компьютере или в другом устройстве вы- числительной техники представляется в виде двоичного цифрового сигнала. Все виды информации (текстовая, графическая, звуковая, видео-) кодируются в последовательности нулей и единиц.
3.1. Алгебра логики
Алгебра логики появилась в середине XIX в. в трудах англий- ского математика Джорджа Буля.
Логическое высказывание – это любое повествовательное пред- ложение, в отношении которого можно однозначно сказать, истинно- го оно или ложно. При этом не всякое предложение является логиче- ским высказыванием. Например, «Хороший студент» не является ло- гическим высказыванием, так как невозможно судить об его истинно- сти или ложности, а высказывание «Иванов – хороший студент» яв- ляется логическим высказыванием.
Употребляемые слова и словосочетания «не», «и», «или», «если,
то», «тогда и только тогда» позволяют из уже заданных высказы- ваний строить новые. Такие слова и словосочетания называются ло-
гическими связками. При этом высказывания, образованные из других высказываний с помощью логических связок, называются составны-

2
ми. Высказывание, не являющееся составным, называется элемен-
тарным.
Для того чтобы обращаться к логическим высказываниям им на- значаются имена. Например, через А обозначим высказывание «Петя был во Франции», а через B высказывание «Петя был в Италии». То- гда составное высказывание примет вид — «Петя был и во Франции, и в Италии», далее можно записать кратко: «A И B». Здесь И – логиче- ская связка, A,B – логические переменные, которые могут принимать только два значения: истинна и ложь, обозначаемые 1 и 0.
В алгебре логики высказывания могут принимать лишь два зна- чения: истинна – 1 и ложь – 0.
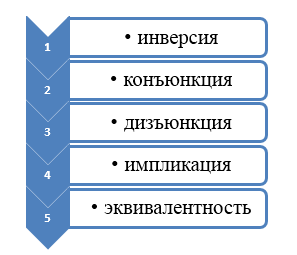
С логическими высказываниями можно производить следующие операции:
1. Операция отрицания (НЕ).
2. Операция конъюнкции (И).
3. Операция дизъюнкции (ИЛИ).
4. Операция импликации (ЕСЛИ…ТО).
5. Операция эквиваленции (ТОГДА, И ТОЛЬКО ТОГДА).
Порядок выполнения логических операций задается круглыми скобками, но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицание (НЕ), затем конъюнк- ции (И), затем дизъюнкции (ИЛИ) и в последнюю очередь — имплика- ции. Это называется приоритетом операций.
3.2. Логические основы устройства компьютера
Логический элемент компьютера – это часть электронной логи- ческой схемы, которая реализует элементарную логическую функ- цию.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также венти- лями), а также триггер.
Триггер — это устройство позволяющее запоминать, хранить и считывать информацию (каждый триггер может хранить 1 бит ин- формации).
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у элементов бывает от 2 до 8 входов и один или два выхода. Чтобы представить два логических состояния 1 и 0, соответствующие им

3 входные и выходные сигналы имеют один из двух установленных уровней напряжения, например 5 и 0 В. Высокий уровень обычно со- ответствует значению «истинна» (1), а низкий – значению «ложь» (0).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая электронная схема в нем реализована. Это упрощает запись и понимание сложных схем.
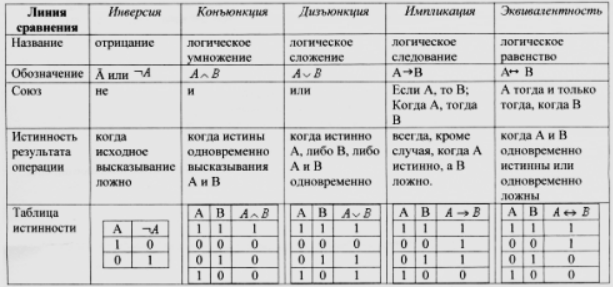
Работу логических элементов описывают с помощью таблиц ис- тинности. Основные структурные схемы логических элементов ком- пьютера и их таблицы истинности, представлены в таблице 1.
Таблица 1
Структурные схемы логических элементов компьютера
Условное обозначение
Структурная схема
(отечественное обозна- чение)
Структурная схема
(зарубежное обозна- чение)
Таблица истинности
И
A
B
Y (A B
C B
C C

3




A C
A
C


4




C
A
B
C B
C C) B
C б) описание хода выполнения работы; в) логическая схема высказывания; г) схема асинхронного RS- триггера; д) таблицы истинности; е) заключение по выполненной работе; ж) ответы на контрольные вопросы.
Контрольные вопросы
1. Что такое логическое высказывание?
2. Какие операции можно производить с высказываниями?
3. Что такое триггер?
4. Какие типы триггеров существуют?
5. Какие структурные схемы у элементов И, НЕ, ИЛИ? Привести таблицы истинности.

Источник: topuch.com

Построение таблиц истинности

Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.

Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.

Определение 2

Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.

Определение 3

Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.

При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:

Приоритетом в выполнении порядка выполнения операций пользуются скобки.

Алгоритм построения таблицы истинности логической функции

1. Определяют количество строк:кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
2. Определяют количество столбцов:кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
3. Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.

«Построение таблиц истинности»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы

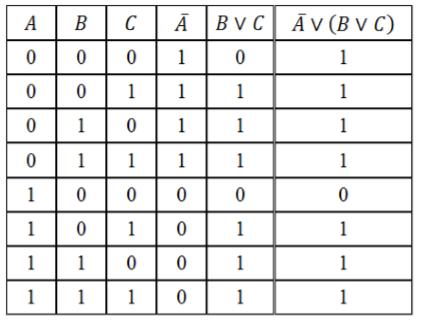
Составить таблицу истинности логического выражения $D=bar vee (B vee C)$.

Решение:

1. Определим количество строк: Количество простых выражений – $n=3$, значит кол-во строк = $2^3 + 1=9$.
2. Определим количество столбцов: Количество переменных – $3$. Количество логических операций и их последовательность:

1. инверсия ($bar$);
2. дизъюнкция, т.к. она находится в скобках ($B vee C$);
3. дизъюнкция ($overlinevee left(Bvee Cright)$) – искомое логическое выражение. Кол-во столбцов = $3 + 3=6$.

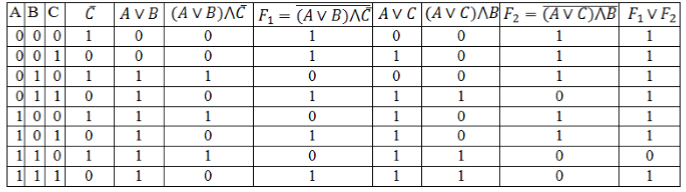
По данному логическому выражению построить таблицу истинности:

Решение:

1. Определим количество строк: Количество простых выражений – $n=3$, значит кол-во строк = $2^3 + 1=9$.
2. Определим количество столбцов: Количество переменных – $3$. Количество логических операций и их последовательность:

1. отрицание ($bar$);
2. дизъюнкция, т.к. она находится в скобках ($A vee B$);
3. конъюнкция ($(Avee B)bigwedge overline$);
4. отрицание, которое обозначим $F_1$ ($overline<(Avee B)bigwedge overline>$);
5. дизъюнкция ($A vee C$);
6. конъюнкция ($(Avee C)bigwedge B$);
7. отрицание, которое обозначим $F_2$ ($overline<(Avee C)bigwedge B>$);
8. дизъюнкция – искомая логическая функция ($overline<(Avee B)bigwedge overline>vee overline<(Avee C)bigwedge B>$). Кол-во столбцов = $3 + 8 = 11$.

Алгоритм построения логической функции по ее таблице истинности

1. Выделяют в таблице истинности строки со значением функции, равным $1$.
2. Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
3. Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
4. В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.

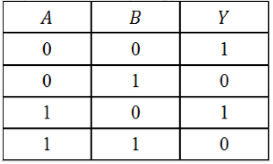
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.

Решение:

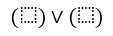
1. Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
2. Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:

Источник: spravochnick.ru