В какой системе счисления представлены программы и данные в памяти компьютера

Внутреннее представление данных в памяти компьютера

Обрабатываемые с помощью компьютера данные записываются в специальных запоминающих устройствах, называемых памятью. Двоичное кодирование используется для представления в компьютере как числовой, так и текстовой, графической, звуковой информации.

Форматы представления данных в памяти компьютера определяют диапазоны значений, которые эти данные могут принимать, скорость их обработки, объем памяти, который требуется для хранения данных. Существуют две формы представления числовых данных, предназначенные для целых и действительных чисел соответственно.

Целые числаточно представляются в памяти компьютера и позволяют выполнять операции без погрешностей. Целочисленная арифметика позволяет реализовать операции деления нацело с остатком (причем можно в качестве результата получить как частное от деления, так и остаток).

Именно целые числа используются при решении многих экономических задач и задач управления (примерами данных, представленных целочисленными величинами, являются количество акций, сотрудников, транспортных средств, деталей, единиц боевой техники и т.п.; целые числа служат для нумерации элементов в различных наборах данных, для обозначения даты и времени, для кодирования текста, изображения и звука), реализации средств криптографической защиты информации (защиты с помощью шифрования), в программах электронной почты и в средствах навигации вInternetдля записи адреса и т.д. Поэтому аппаратурой компьютеров обычно поддерживается несколько форматов представления целочисленных данных и множество операций над ними.

8 класс — Информатика — Представление чисел в памяти компьютера

Целые числа в памяти компьютера всегда хранятся в формате сфиксированной точкой, что, безусловно, ограничивает диапазон чисел, с которыми может работать компьютер, и требует учета особенностей организации выполнения арифметических действий в ограниченном числе разрядов. Рассмотрим подробнее это представление.

Все числа, которые хранятся в памяти компьютера, занимают определенное количество двоичных разрядов. Это количество определяется форматом числа. Обычно для представления целых чисел используются несколько форматов (например, в IBM-совместимых персональных компьютерах поддерживается три формата: байт (8 разрядов), слово (16 разрядов), двойное слово (32 разряда)).

Целые числа вписываются в разрядную сетку, соответствующую формату. Для целых чисел разрядная сетка имеет вид: где b i– разряды двоичной записи целого числа (запись числа имеет видb n–2b n–3. b 1b 0, разделитель между целой и дробной частью числа зафиксирован послеb0, дробной части нет);S– разряд, отведенный для представления знака числа (для положительных чисел знак «+» кодируется цифрой 0, а знак «–» для отрицательных – цифрой 1);n– количество двоичных разрядов в разрядной сетке.

Если двоичная запись числа оказывается короче отведенной для его хранения в памяти компьютера разрядной сетки, то старшие разряды заполняются нулями. Например, число 1110=10112в формате байта будет записано так:

(старший (знаковый) разряд заштрихован).

СИСТЕМЫ СЧИСЛЕНИЯ С НУЛЯ | ОСНОВЫ ПРОГРАММИРОВАНИЯ

В формате слова (16 разрядов) то же число будет выглядеть так: Отрицательные числа для упрощения выполнения операций хранятся в дополнительном коде, который получается путем обращения (инверсии) всех разрядов в двоичной записи числа, вписанной в разрядную сетку, и добавления 1. Например, число –1110в формате байта в памяти компьютера будет получено следующим образом. Вычисляется прямой код:

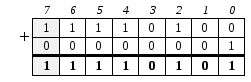затем выполняется инверсия полученного прямого кода (получается обратный код): к обратному коду прибавляется 1: получается дополнительный код – запись отрицательного числа –1110в памяти компьютера: Такая запись чисел ограничивает диапазоны значений, с которыми может работать компьютер.

Например, для чисел в формате байта представимы значения от –128 (–2 7 ) до 127 (2 7 –1), для чисел в формате слова – от –32 768 (–2 15 ) до 32 767 (2 15 –1), а длинные целые числа в формате двойного слова могут принимать значения из диапазона от –2 147 483 648 до 2 147 483 647. Если по условиям задачи используются только положительные значения, то их можно хранить в формате чисел без знака – старший разряд рассматривается как разряд, содержащий двоичную цифру записи числа, а не знак.

При этом диапазон представимых положительных чисел увеличивается. Например, в байт можно записать числа от 0 до 255 (2 8 –1), а в слово – значения от 0 до 65535 (2 16 –1). Особенности представления чисел в памяти компьютера могут привести и к ошибкам при обработке данных. Рассмотрим пример.

Предположим, что программа выполняет функции подсчета каких-либо объектов, и для хранения количества этих объектов используется представление данных в формате целого числа со знаком, записанного в байт. Рассмотрим ситуацию, когда количество объектов уже стало равным 127 и увеличивается еще на 1. Результат должен быть равен 128, но сможем ли мы его получить с помощью компьютера, если работаем со знаковыми числами в формате байта?

Целое число 127 в памяти компьютера будет представлено цепочкой нулей и единиц 01111111. При добавлении единицы будет получено число 10000000: 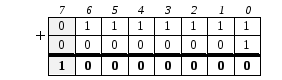(действия в двоичной системе счисления выполняются так же, как и в десятичной, но используются только две цифры, поэтому, если при сложении разрядов получается значение большее 1, происходит перенос в старший разряд).

Но старший разряд является знаковым! Поэтому в результате сложения компьютер получит целое число –128, записанное своим дополнительным кодом. И именно это отрицательное число будет затем использовано во всех вычислениях. Этот пример демонстрирует возможность появления ошибок при выполнении программ вследствие неправильно выбранных форматов для представления данных.

Таким образом, при выполнении программ может возникнуть ситуация, когда полученные результаты не смогут «вписаться» в отведенную для них разрядную сетку, произойдет ее «переполнение». Разработчики программ должны отслеживать такие ситуации и предотвращать подобные ошибки, а пользователи должны четко формулировать требования к условиям эксплуатации программ, их входным данным и результатам.

Игнорирование этих требований может создать серьезные проблемы. Поэтому при разработке программного обеспечения очень важно знать, с какими диапазонами значений будет работать программа. Это позволит правильно определить форматы представления чисел и предупредить возможные ошибки при обработке данных.

Каждый раз при вводе данных в компьютер происходит преобразование числовых данных, введенных пользователем с клавиатуры в виде строки символов, представляющей десятичную запись числа, во внутреннее двоичное представление числа. При выводе результатов осуществляются обратные преобразования. Эти преобразования требуют времени.

Поэтому для систем, в которых вводится и выводится большой объем информации, осуществляется ее поиск, происходит замедление выполнения программ вследствие постоянных переводов информации из одной формы представления в другую. Для представления данных в таких системах (а именно к ним относится большинство программ для решения экономических задач и задач управления) используется еще одна форма представления данных в памяти компьютера – двоично-десятичные данные.

При использовании двоично-десятичнойформы представления данных десятичные числа также представляются с помощью двоичных кодов, но в двоичную систему переводится не все число, а каждая его цифра отдельно. Так как используется всего десять десятичных цифр от 0 до 9, а для представления старшей цифры 9 достаточно четырех двоичных цифр (910=10012), то каждая десятичная цифра в записи числа кодируется четырьмя двоичными цифрами в его двоично-десятичном представлении в памяти компьютера.

Например, число 105910представляется в памяти компьютера следующим образом: Двоично-десятичные данные могут использоваться не только для представления целых чисел, но и для представления чисел, имеющих дробную часть. Знак числа и позиция десятичного разделителя в нем кодируются отдельно.

Для двоично-десятичных чисел также существуют различные форматы записи чисел в памяти компьютера. Конкретные форматы определяются его архитектурными особенностями. При использовании двоично-десятичного представления проще выполняется преобразование данных при вводе/выводе, но усложняются алгоритмы выполнения операций.

Поэтому такая форма представления применяется там, где данные не подвергаются сложной обработке, где нет объемных вычислений. Решение проблем математического моделирования в естественных науках, экономике и технике, работа с системами автоматического проектирования, электронными таблицами невозможны без использования вещественных (действительных) чисел.

Для представления этих чисел разработана специальная форма – данные в памяти компьютера хранятся в форме с плавающей точкой. Такое представление основано на записи числа в экспоненциальном виде, где разряды в записи числа представляются мантиссойM, а положение точки определяется указанием порядкаp:M10p . При использовании такой формы представления часть разрядов разрядной сетки, в которую помещается число в памяти компьютера, отводится для хранения порядка числа p, а остальные разряды – для хранения мантиссыM:

Порядок числа и его мантисса хранятся в двоичном коде, поэтому перед их определением число переводится в двоичную систему.

Точность вычислений зависит от длины мантиссы, а порядок числа определяет допустимый диапазон представления действительных чисел. Например, в IBM-совместимых персональных компьютерах используются три формата представления данных в форме с плавающей точкой (32 разряда, 64 разряда и 80 разрядов), позволяющие представлять три диапазона положительных вещественных чисел: от 1,510 ‑45 до 3,410 38 , от 510 324 до 1,710 308 и от 1,910 4951 до 1,110 4932 . Для представления положительных чисел в знаковый разряд записывается значение 0, а отрицательных чисел – 1. Порядок и мантисса записываются как целые числа.

Такая форма представления чисел усложняет функциональную схему компьютера, так как операции над числами с плавающей точкой значительно сложнее. Для ускорения обработки числовых данных в его состав включаются специальные устройства.

Особенности представления вещественных чисел в памяти компьютера определяют свойства машинных чисел: при переводе дробной части десятичного числа в формат с плавающей точкой происходит его округление до количества разрядов, определяемых длиной мантиссы; ограниченная длина мантиссы приводит к погрешности при выполнении операций («лишние» разряды отсекаются или происходит округление); вещественные числа нельзя сравнивать на равенство, их можно только проверять на принадлежность определенным диапазонам. Текстовые данныерассматриваются как последовательность отдельных символов, каждому из которых ставится в соответствие двоичный код некоторого неотрицательного целого числа.

Существуют разные способы кодирования символов. Наиболее распространенной до последнего времени была кодировка ASCII(AmericanStandardCodeforInformationInterchange). При использовании этой кодировки для представления каждого символа используется ровно 8 разрядов (один байт). Таким образом, имеется возможность кодирования 256 символов (они получают коды от 0 до 255).

С помощью такой кодировки можно хранить только символы текста (без элементов форматирования или оформления). Для отображения текстового документа с разбивкой его на строки, с выравниванием и т.п. в него наряду с обычными символами, представляющими буквы, цифры, знаки препинания, разделители, включаются специальные (управляющие) символы (например: «перевод строки», «возврат каретки», «табуляция» и т.д.).

Соответствие символов и их кодов можно установить с помощью специальной таблицы. В России используются элементы таблицы альтернативной модифицированной кодировки, в первой части которой размещены символы ASCII(цифры, буквы латинского алфавита, знаки препинания, управляющие символы), а во второй половине – буквы русского алфавита, символы псевдографики, которые позволяют включить в текст простейшие рисунки и таблицы, составленные из вертикальных и горизонтальных линий).

ASCIIпозволяет закодировать только 256 символов. Это неудобно, так как существуют языки, где символов больше. Поэтому разрабатываются другие коды (наборы символов), например двухбайтовые наборы символов (DBCS–double-bytecharactersets).

В этом двухбайтовом коде символы представляются одним и двумя байтами, что неудобно для организации обработки такой информации (для каждого символа сначала нужно определить длину его кода, а уж потом сам символ). Наиболее перспективным для использования является Unicode– стандарт, разработанный несколькими фирмами (сначала –AppleиXerox). В этом коде все символы состоят из 16 битов.

Это позволяет кодировать свыше 65 тыс. символов (2 16 ). В этом коде для каждого алфавита определены своикодовые позиции(codepoints), т.е. все 65536 символов (кодов) разбиты на отдельные группы (например: 0100-017F – европейские латинские, 0180-01FF– расширенные латинские, 0250-02AF– стандартные фонетические, 0370-03FF– греческий, 0400-04FF– кириллица и т.д.). Около 29 000 кодовых позиций пока не заняты, но зарезервированы для использования.

Таким образом,Unicodeдопускает обмен данными на разных языках – каждому коду соответствует единственный символ, коды не пересекаются для разных языков. На Unicodeцеликом построена операционная системаWindows NT. УWindows 95/98 16‑битное «наследство», поэтому вся внутренняя работа в этой ОС построена на использованииANSI-строк (ANSI–AmericanNationalStandardsInstitute), в которых каждый символ записан в один байт.

ANSI-текст (или текстASCII) – это текст без форматирования (с ним работает, например, приложение «Блокнот» вWindows 9х). Если для представления информации в разных информационных системах используются разные кодировки, эти программы «не поймут» друг друга, поэтому может оказаться, что данные, подготовленные в одном месте, не смогут прочитать в другом.

Например, текст, введенный с помощью программы «Блокнот» в Windows, нельзя будет прочитать вMS‑DOS. Способ представления графических изображений, отображаемых на экране, называютматричным.

При этом экран дисплея ЭВМ рассматривается как двумерный массив отдельных точек (пикселов), состояние каждой из которых (цвет и яркость) кодируется неотрицательным целым двоичным числом. Звукпредставляет собой непрерывный сигнал, колебания частиц среды, распространяющиеся в виде волн и воспринимаемые органами слуха.

Чтобы закодировать звук, его надо сначала подвергнуть дискретизации. Этот процесс состоит в измерении и запоминании в памяти компьютера характеристик звуковой волны (амплитуды и периода) в виде двоичного кода, он выполняется аналого-цифровым преобразователем несколько десятков тысяч раз в секунду через равные промежутки времени.

При воспроизведении двоичные коды подаются на вход цифро-аналогового преобразователя с той же частотой, что и при дискретизации, преобразуются в электрическое напряжение, а затем с помощью усилителя и динамика – в звук. Такой способ звукозаписи, называемыйцифровым, требует большого объема памяти компьютера, у оцифрованного звука трудно менять тональность или тембр. Для кодирования музыки чаще используется не запоминание параметров звуковых волн, а запись последовательности команд, например: какую клавишу нажать, какова сила давления, сколько времени удерживать клавишу нажатой и т.д. ТакаяMIDI–запись аналогична нотной записи. Она компактна, в ней легко производится смена инструмента или тональность мелодии. 14

Ограничение

Для продолжения скачивания необходимо пройти капчу:

Источник: studfile.net

Представление данных и архитектура ЭВМ

Двоичная, восьмеричная и шестнадцатеричная системы счисления

Смешанные системы счисления

Перевод чисел в различные системы счисления

Двоичная арифметика

Прямой, обратный и дополнительный коды

Кодирование символов

История развития вычислительной техники

Архитектура вычислительных машин

Структура и форматы машинных команд

Подавляющее большинство современных вычислительных машин построено по принципу архитектуры фон Неймана. В функциональном устройстве компьютера можно выделить следующие основные блоки:

• устройства ввода-вывода (УВВ),
• память,
• центральный процессор.

Все они взаимодействуют между собой через системную шину.

Устройства ввода принимают закодированную информацию от операторов, электромеханических устройств (клавиатура, мышь) или от других компьютеров сети. Полученная информация либо сохраняется в памяти компьютера для дальнейшего использования, либо немедленно используется АЛУ для выполнения необходимых операций. Последовательность шагов обработки определяется хранящейся в памяти программой. Полученные результаты обратно отправляются получателю посредством устройств вывода. Все эти действия координируются устройством управления.

Основные принципы построения ЭВМ

Основные принципы построения ЭВМ были сформулированы американским ученым Джоном фон Нейманом в 40-х годах 20 века:

• Принцип двоичности. Для представления данных и команд используется двоичная система счисления.
• Принцип программного управления. Программа состоит из набора команд, которые выполняются процессором друг за другом в определённой последовательности.
• Принцип однородности памяти. Как программы (команды), так и данные хранятся в одной и той же памяти (и кодируются в одной и той же системе счисления, чаще всего – двоичной). Над командами можно выполнять такие же действия, как и над данными.
• Принцип адресуемости памяти. Структурно основная память состоит из пронумерованных ячеек, процессору в произвольный момент времени доступна любая ячейка.
• Принцип последовательного программного управления. Все команды располагаются в памяти и выполняются последовательно, одна после завершения другой.
• Принцип условного перехода. Команды из программы не всегда выполняются одна за другой. Возможно присутствие в программе команд условного перехода, которые изменяют последовательность выполнения команд в зависимости от значений данных. (Сам принцип был сформулирован задолго до фон Неймана Адой Лавлейс и Чарльзом Бэббиджем, однако он логически включен в фоннеймановский набор как дополняющий предыдущий принцип).

Комментариев к записи: 2

Frizzle Fraz 2

Существует большое разнообразие сложных типов данных, но исследования, проведенные на большом практическом материале, показали, что среди них можно выделить несколько наиболее общих. Обобщенные структуры называют также

Источник: prog-cpp.ru

ПРЕДСТАВЛЕНИЕ ДАННЫХ В ПАМЯТИ ПЕРСОНАЛЬНОГО КОМПЬЮТЕРА (ЧИСЛА, СИМВОЛЫ, ГРАФИКА, ЗВУК)

Вся информация, которую обрабатывает компьютер, должна быть представлена двоичным кодом с помощью двух цифр — 0 и 1. Эти два символа принято называть двоичными цифрами, или битами. С помощью двух цифр 1 и 0 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организовано два важных процесса:

• · кодирование, которое обеспечивается устройствами ввода при преобразовании входной информации в форму, воспринимаемую компьютером, то есть в двоичный код;
• · декодирование, которое обеспечивается устройствами вывода при преобразовании данных из двоичного кода в форму, понятную человеку.

С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намногоболее простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:

• · 0 — отсутствие электрического сигнала или сигнал имеет низкий уровень;
• · 1 — наличие сигнала или сигнал имеет высокий уровень.

Эти состояния легко различать. Недостаток двоичного кодирования — длинные коды. Но в технике легче иметь дело с большим числом простых элементов, чем с небольшим количеством сложных.

Вам и в быту ежедневно приходится сталкиваться с устройством, которое может находиться только в двух устойчивых состояниях: включено/выключено. Конечно же, это хорошо знакомый всем выключатель. А вот придумать выключатель, который мог бы устойчиво и быстро переключаться в любое из 10 состояний, оказалось невозможным. В результате после ряда неудачных попыток разработчики пришли к выводу о невозможности построения компьютера на основе десятичной системы счисления. И в основу представления чисел в компьютере была положена именно двоичная система счисления.

В настоящее время существуют разные способы двоичного кодирования и декодирования информации в компьютере. В первую очередь это зависит от вида информации, а именно, что должно кодироваться: текст, числа, графические изображения или звук. Кроме того, при кодировании чисел важную роль играет то, как они будут использоваться: в тексте, в расчетах или в процессе ввода-вывода. Накладываются также и особенности технической реализации.

Кодирование чисел

Система счисления — совокупность приемов и правил записи чисел с помощью определенного набора символов. Для записи чисел могут использоваться не только цифры, но и буквы (например, запись римских цифр — XXI). Одно и то же число может быть по-разному представлено в различных системах счисления. В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра этого числа. Например, меняя позицию цифры 2 в десятичной системе счисления, можно записать разные по величине десятичные числа, например 2; 20; 2000; 0,02 и т. д.

В непозиционной системе счисления цифры не изменяют своего количественного значения при изменении их расположения (позиции) в числе. Примером непозиционной системы может служить римская система, в которой независимо от местоположения одинаковый символ имеет неизменное значение (например, символ X в числе XXV).

Количество различных символов, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления.

В компьютере наиболее подходящей и надежной оказалась двоичная система счисления, в которой для представления чисел используются последовательности цифр 0 и 1. Кроме того, для работы с памятью компьютера оказалось удобным использовать представление информации с помощью еще двух систем счисления:

• · восьмеричной ( любое число представляется с помощью восьми цифр — 0, 1, 2. 7);
• · шестнадцатеричной (используемые символы-цифры — 0, 1, 2. 9 и буквы — А, В, С, D, Е, F, заменяющие числа 10, 11, 12, 13, 14, 15 соответственно).

Кодирование символьной информации

Нажатие алфавитно-цифровой клавиши на клавиатуре приводит к тому, что в компьютер посылается сигнал в виде двоичного числа, представляющего собой одно из значений кодовой таблицы. Кодовая таблица — это внутреннее представление символов в компьютере. Во всем мире в качестве стандарта принята таблица ASCII (American Standart Code for Informational Interchange — американский стандартный код информационного обмена).

Для хранения двоичного кода одного символа выделен 1 байт = 8 бит. Учитывая, что каждый бит принимает значение 1 или 0, количество возможных сочетаний единиц и нулей равно 2 8 = 256.

Значит, с помощью 1 байта можно получить 256 разных двоичных кодовых комбинаций и отобразить с их помощью 256 различных символов. Эти коды и составляют таблицу ASCII.

Пример, при нажатии клавиши с буквой S в память компьютера записывается код 01010011. При выводе буквы 8 на экран компьютер выполняет декодирование — на основании этого двоичного кода строится изображение символа.

SUN (СОЛНЦЕ) — 01010011 010101101 01001110

Стандарт ASCII кодирует первые 128 символов от 0 до 127: цифры, буквы латинского алфавита, управляющие символы. Первые 32 символа являются управляющими и предназначены в основном для передачи команд управления. Их назначение может варьироваться в зависимости от программных и аппаратных средств. Вторая половина кодовой таблицы (от 128 до 255) американским стандартом не определена и предназначена для символов национальных алфавитов, псевдографических и некоторых математических символов. В разных странах могут использоваться различные варианты второй половины кодовой таблицы.

Цифры кодируются по стандарту ASCII записываются в двух случаях — при вводе-выводе и когда они встречаются я тексте. Если цифры участвуют в вычислениях, то осуществляется их преобразование в другой двоичный код.

Для сравнения рассмотрим число 45 для двух вариантов кодирования.

При использовании в тексте это число потребует для своего представления 2 байта, поскольку каждая цифра будет представлена своим кодом в соответствии с таблицей ASCII . В двоичной системе — 00110100 00110101.

При использовании в вычислениях код этого числа будет получен по специальным правилам перевода и представлен в виде 8-разрядного двоичного числа 00101101, на что потребуется 1 байт.

Кодирование графической информации

Создавать и хранить графические объекты в компьютере можно двумя способами — как растровое или как векторное изображение. Для каждого типа изображения используется свой способ кодирования.

Растровое изображение представляет собой совокупность точек, используемых для его отображения на экране монитора. Объем растрового изображения определяется как произведение количества точек и информационного объема одной точки, который зависит от количества возможных цветов. Для черно-белого изображения информационный объем одной точки равен 1 биту, так как точка может быть либо черной, либо белой, что можно закодировать двумя цифрами — 0 или 1.

Для кодирования 8 цветов необходимо 3 бита; для 16 цветов — 4 бита; для 256 цветов — 8 битов (1 байт) и т.д.

Векторное изображение представляет собой совокупность графических примитивов. Каждый примитив состоит из элементарных отрезков кривых, параметры которых (координаты узловых точек, радиус кривизны и пр.) описываются математическими формулами. Для каждой линии указываются ее тип (сплошная, пунктирная, штрих-пунктирная), толщина и цвет, а замкнутые фигуры дополнительно характеризуются типом заливки. Кодирование векторных изображений выполняется различными способами в зависимости от прикладной среды. В частности, формулы, описывающие отрезки кривых, могут кодироваться как обычная буквенно-цифровая информация для дальнейшей обработки специальными программами.

Кодирование звуковой информации

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).

В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие участки, причем для каждого такого участка устанавливается определенная величина амплитуды.Таким образом, непрерывная зависимость амплитуды сигнала от времени заменяется на дискретную последовательность уровней громкости.

Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. В таком случае количество уровней сигнала будет равно 65536.

При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т.е. от частоты дискретизации. Чем больше количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.

Количество измерений в секунду может лежать в диапазоне от 8000 до 48000, т.е. частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц — качество звучания аудио-CD. Следует также учитывать, что возможны как моно-, так и стерео-режимы.

Стандартная программа Windows Звукозапись играет роль цифрового магнитофона и позволяет записывать звук, т.е. дискретизировать звуковые сигналы, и сохранять их в звуковых файлах в формате wav. Также эта программа позволяет производить простейшее редактирование звуковых файлов.

Источник: vuzlit.com