Как вы уже знаете, числа – это хлеб с маслом компьютера, фундаментальная основа всего, что он делает. Любая информация, которую вы отправляете компилятору, в конечном итоге становится числом. Например, каждый символ в блоке текста представлен числом.
Изображения не являются исключением. В компьютере каждое изображение также представлено серией чисел. Изображение состоит из многих тысяч или даже миллионов элементов изображения, называемых пикселями, где каждый пиксель – это сплошной цвет.
Если вы внимательно посмотрите на экран своего компьютера, вы сможете различить эти блоки. Если только у вас не дисплей с особенно высоким разрешением, где пиксели невероятно малы!
Каждый из этих пикселей сплошного цвета обычно представлен тремя числами: одно – количество красного цвета, другое – количество зеленого и третье – количество синего. Например, полностью красный пиксель будет иметь 100% красного, 0% зеленого и 0% синего.
Числа, с которыми работает процессор, заметно отличаются от тех, к которым вы привыкли. Когда вы имеете дело с числами в повседневной жизни, вы работаете с ними по основанию 10, известному также как десятичная система. Используя эту систему счисления, вы интуитивно понимаете, как она работает. Чтобы вы могли оценить точку зрения процессора, рассмотрим, как работает основание 10.
СИСТЕМЫ СЧИСЛЕНИЯ С НУЛЯ | ОСНОВЫ ПРОГРАММИРОВАНИЯ
Десятичное число 423 содержит три единицы, два десятка и четыре десятка.
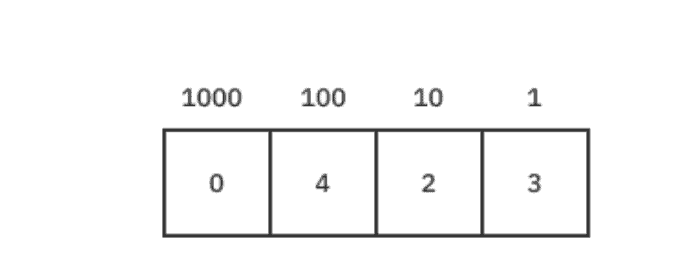
В системе счисления по основанию 10 каждая цифра числа может иметь значение 0, 1, 2, 3, 4, 5, 6, 7, 8 или 9, что дает в общей сложности 10 возможных значений для каждой цифры. Но фактическое значение каждой цифры зависит от ее положения в числе.
Двигаясь справа налево, каждая цифра умножается на возрастающее значение 10. Так, множитель для крайней правой цифры равен 10 в степени 0, то есть 1. Двигаясь влево, следующий множитель равен 10 в степени 1, то есть 10. Если снова переместиться влево, то следующий множитель будет равен 10 в степени 2, то есть 100. И так далее.
Это означает, что каждая цифра имеет значение, в десять раз превышающее значение цифры справа от нее. Число 423 равно следующему:
(0 * 1000) + (4 * 100) + (2 * 10) + (3 * 1) = 423
Двоичная система
Поскольку вас учили работать с десятичной системой, вам не нужно думать о том, как считать большинство чисел – это кажется вполне естественным. Но для компьютера десятичная система – это слишком сложно! Компьютеры просты, помните? Им нравится работать с двоичной системой.
В двоичной системе есть только два варианта для каждой цифры: 0 или 1.
Почти все современные компьютеры используют двоичную систему, потому что на физическом уровне проще всего работать только с двумя вариантами для каждой цифры. В цифровых электронных схемах, из которых в основном и состоит компьютер, наличие электрического напряжения равно 1, а его отсутствие равно 0.
Простой перевод в любую систему счисления
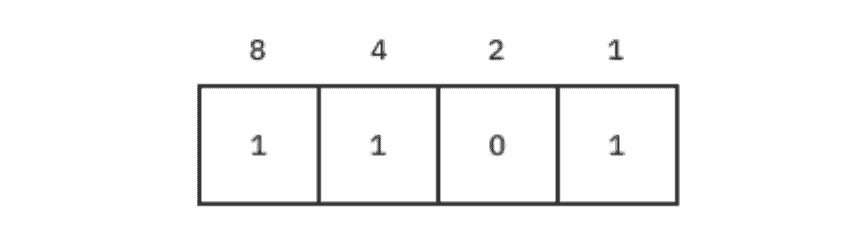
Вот представление числа 1101 в двоичной системе:
В десятичной системе значения увеличиваются в 10 раз: 1, 10, 100, 1000 и т. д. В двоичной системе счисления они увеличиваются в 2 раза: 1, 2, 4, 8, 16 и т. д. Общее правило заключается в умножении каждой цифры на возрастающую силу основного числа – в данном случае на силу 2 – двигаясь справа налево.
Так, крайняя правая цифра представляет собой (1 * 2^0), то есть (1 * 1), то есть 1. Следующая цифра слева представляет собой (0 * 2^1), то есть (0 * 2), то есть 0.
Говоря иначе, каждая 2 либо есть (1), либо нет (0) в качестве компонента двоичного числа. Десятичная версия двоичного числа представляет собой сумму всех степеней 2, составляющих это число. Таким образом, двоичное число 1101 равно:
(1 * 8) + (1 * 4) + (0 * 2) + (1 * 1) = 13
А если бы вы захотели перевести число 423 в двоичную систему счисления, то вам просто нужно было бы разложить 423 на составляющие его степени 2. В итоге вы получили бы следующее:
(1 * 256) + (1 * 128) + (0 * 64) + (1 * 32) + (0 * 16) + (0 * 8) + (1 * 4) + (1 * 2) + (1 * 1) = 423
Как вы можете видеть, сканируя двоичные цифры в приведенном выше уравнении, результирующее двоичное число равно 110100111. Вы можете доказать себе, что оно равно 423, выполнив математические действия!
Компьютерный термин, обозначающий каждую цифру двоичного числа, – бит (сокращение от “двоичный разряд”). Восемь битов составляют байт.
Ограниченная память компьютера означает, что он обычно может работать с числами определенной длины. Каждый регистр, например, обычно имеет длину 32 или 64 бита, поэтому мы говорим о 32-битных и 64-битных процессорах.
Таким образом, 32-битный процессор может обрабатывать максимальное число 4 294 967 295, что является основанием 2 числа 1111111111111111111111111111111111111111111111. Это 32 единицы – посчитайте их!
Компьютер может обрабатывать числа, превышающие максимальное значение процессора, но вычисления должны быть разделены и управляться особым и более длинным способом.
Шестнадцатеричная система
Как вы можете себе представить, работа с двоичными числами может стать довольно утомительной, поскольку их написание или ввод может занять много времени. По этой причине в компьютерном программировании мы часто используем другой формат чисел, известный как шестнадцатеричный, или сокращенно hex.
Конечно, для цифр не существует 16 отдельных чисел, их всего 10. Чтобы дополнить их, мы используем первые шесть букв, от a до f.
Они эквивалентны десятичным числам следующим образом:
Приведем пример с основанием 16, используя тот же формат, что и раньше:
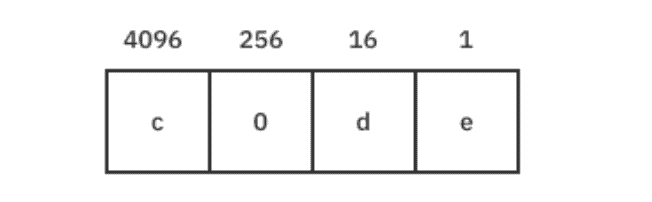
Прежде всего, обратите внимание, что шестнадцатеричные числа можно сделать похожими на слова. Это означает, что вы можете немного повеселиться.
Теперь значения каждой цифры относятся к числам, равным 16. Точно так же, как и раньше, вы можете перевести это число в десятичную систему счисления следующим образом:
(12 * 4096) + (0 * 256) + (13 * 16) + (14 * 1) = 49374
Вы переводите буквы в их десятичные эквиваленты, а затем выполняете обычные вычисления.
Шестнадцатеричное исчисление полезно тем, что каждая шестнадцатеричная цифра может представлять ровно четыре двоичные цифры. Двоичное число 1111 эквивалентно шестнадцатеричному f.
Из этого следует, что вы можете просто объединить двоичные цифры, представляющие каждую шестнадцатеричную цифру, создав шестнадцатеричное число, которое короче, чем его двоичный или десятичный эквивалент.
Например, рассмотрим число c0de, приведенное выше:
c = 1100 0 = 0000 d = 1101 e = 1110 c0de = 1100 0000 1101 1110
Это оказывается весьма полезным, учитывая, как компьютеры используют длинные 32- или 64-битные двоичные числа. Вспомните, что самое длинное 32-битное число в десятичной системе счисления – 4 294 967 295. В шестнадцатеричном виде оно равно ffffffff. Это гораздо компактнее и понятнее.
Источник: swiftblog.org
2.2. Системы счисления, используемые в компьютерах
Совокупность названий и знаков, позволяющая записать любое число и дать ему имя, называется системой счисления или нумерацией.
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
- двоичная (используются цифры 0, 1);
- восьмеричная (используются цифры 0, 1, . 7);
- шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, . 9, а для следующих чисел — от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Источник: studfile.net
Глава 4.Какие системы счисления используют специалисты для работы с компьютером?
Перед математиками и конструкторами в 50-х встала проблема отыскания таких систем счисления, которые отвечали бы требованиям, как разработчиков ЭВМ, так и создателей программного обеспечения. Одним из итогов этих исследований стало значительное изменение представлений о системах счисления и о методах вычислений. Оказалось, что арифметический счет, которым человечество пользуется с древнейших времен, может совершенствоваться, подчас весьма неожиданно и на удивление эффективно.
Специалисты выделили так называемую “машинную” группу систем счисления и разработали способы преобразования чисел этой группы.
К “машинным” системам счисления относятся:
· Двоичная (используются цифры 0, 1);
· Восьмеричная (используются цифры 0, 1. 7);
· Шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1. 9, а для следующих чисел — от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Официальное рождение двоичной арифметики связано с именем Г.В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами.
Почему люди используют десятичную систему счисления, а компьютеры — двоичную, восьмеричную, шестнадцатеричную?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
· представление информации посредством только двух состояний надежно и помехоустойчиво;
· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
· двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетроды (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной.
Заключение.
В основной части рассмотрены были рассмотрены 10 древних систем счисления, история развития систем счисления. Из всех рассмотренных систем счисления, наиболее интересной мне показалась древне-китайская нумерация. Так как она наиболее близка к нашей «арабской» системе счисления. Наиболее красивые цифры и числа в древнеегипетской системе счисления. В ходе исследования я выяснил каким образом в древности вели устный счет (сложение, вычитание, умножение и деление), а также как использовались счетные доски (например, греческий абак), как с помощью древних цифр происходило представление дробей, какие системы счисления использовали разные народы.
Также я выяснил, что двоичная система счисления намного старше электронных машин. Двоичной системой счисления люди интересуются давно. Особенно сильным это увлечение было с конца 16 до 19 века. Знаменитый Лейбниц считал двоичную систему счисления простой, удобной, красивой.
Даже по его просьбе была выбита медаль в честь этой «диадической» системы (так называли тогда двоичную систему счисления).Двоичная система счисления наиболее проста и удобна для автоматизации. Наличие в системе всего лишь двух символов упрощает их преобразование в электрические сигналы. Из любой системы счисления можно перейти к двоичному коду. Почти все ЭВМ используют либо непосредственно двоичную систему счисления, либо двоичное кодирование какой-либо другой системы счисления.
Но двоичная система имеет и недостатки:
— ею пользуются только для ЭВМ;
— быстрый рост числа разрядов, необходимых для записи чисел.
Литература
1. Гашков С.Б. Системы счисления и их применение. МЦНМО, 2004г.
2. Угринович Н.Т. Информатика и информационные технологии. Учебник для 10–11 классов. – М.: Лаборатория Базовых Знаний. 2003.
3.Энциклопедия “ВикипедиЯ” [Электронный ресурс]: Режим доступа: http://ru.wikipedia.org, свободный
4.Урнов В.А. и др. Преподавание информатики в компьютерном классе, М.: Просвещение, 1990, стр. 17
5.Заварыкин В.М. Основы информатики и вычислительной техники, М.: Просвещение, 1989, стр.19
6.Гейн А.Г. Основы информатики и вычислительной техники, М.: Просвещение, 1992, стр.231
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru