В какой программе можно построить сечение

Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений являет­ся основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью.

Юртаева Екатерина Андреевна

Содержимое разработки

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

Реферат

Алгоритмы построения сечений поверхностей
в специальных программных средствах

по дисциплине

Визуализация решений математических задач

Выполнила: студентка группы МДИ-114

Как строить сечения

Проверила: доцент, канд. физ.- мат. наук

Кормилицына Т. В.

1 Особенности построения сечений многогранников в программных средствах…………………………………………….

Список использованных источников…………. …………………

1 Особенности построения сечений многогранников в программных средствах

Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений являет­ся основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью.

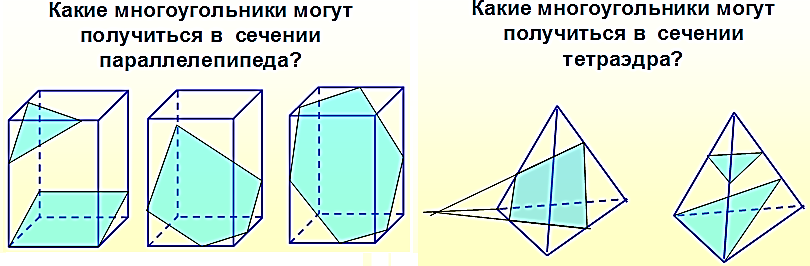
В работе будет рассмотрено построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани, c использованием программы GeoGebra.

Решение задач на построение сечений облегчается с помощью различных компьютерных программ. Одной из таких программ является программное обеспечение динамической математики GeoGebra. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.

Рассмотрим применение этого программного продукта на конкретном примере.

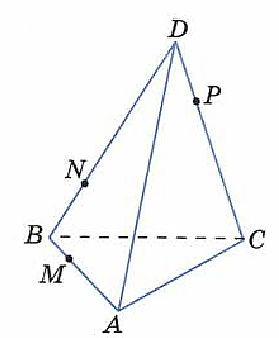
На ребрах AB, BC, CD тетраэдра DABC отмечены точки M, N, P. Построить сечение тетраэдра плоскостью MNP.

1. Откроем программу GeoGebra.
2. В меню Вид выберем Полотно 3D (Полотно 2D можно закрыть).
3. С помощью инструмента создадим тетраэдр DABC.
4. С помощью инструмента на ребрах AB, BC, CD тетраэдра DABC отметим точки M, N, P (переименовать точку можно выделив ее и вызывая контекстное меню правой кнопкой мыши, выбрать соответствующий пункт).
5. Построим прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E, которая и будет второй общей точкой плоскостей MNP и ABC. Для этого выбрав инструмент нужно щелкнуть поочерёдно по точкам N, P и B, C и с помощью инструмента отметить точку E – точку пересечения прямых NP и BC.

Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q.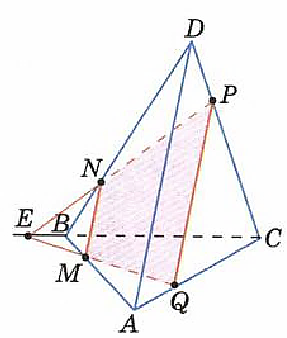

1. Проведём прямую ME выбрав инструмент и щелкнув поочерёдно по точкам M, E. С помощью инструмента отметим точку Q – точку пересечения прямой ME и ребра AC.
2. Четырёхугольник МNPQ – искомое сечение. Выделим его используя инструмент поочерёдно щелкая по точками M, N, P, Q, M.
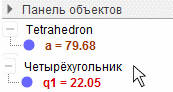
3. Дважды щелкнув по объектам Tetrahedron и Четырёхугольник (рис. 3) можно вызвать контекстное меню с настройками, в которых можно выбрать цвет заливки и прозрачность соответствующего объекта. рис. 3

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnline

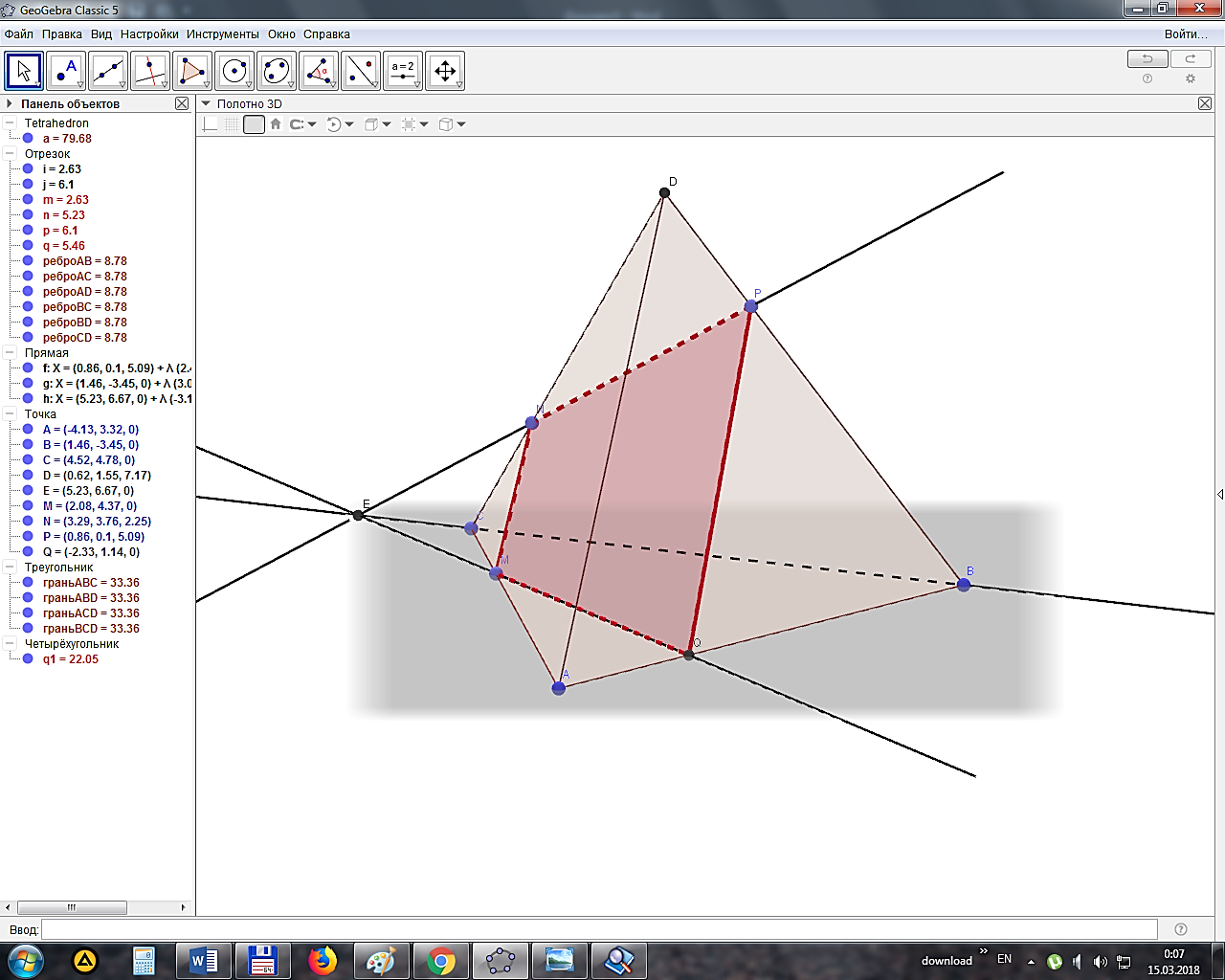3 Задача 2
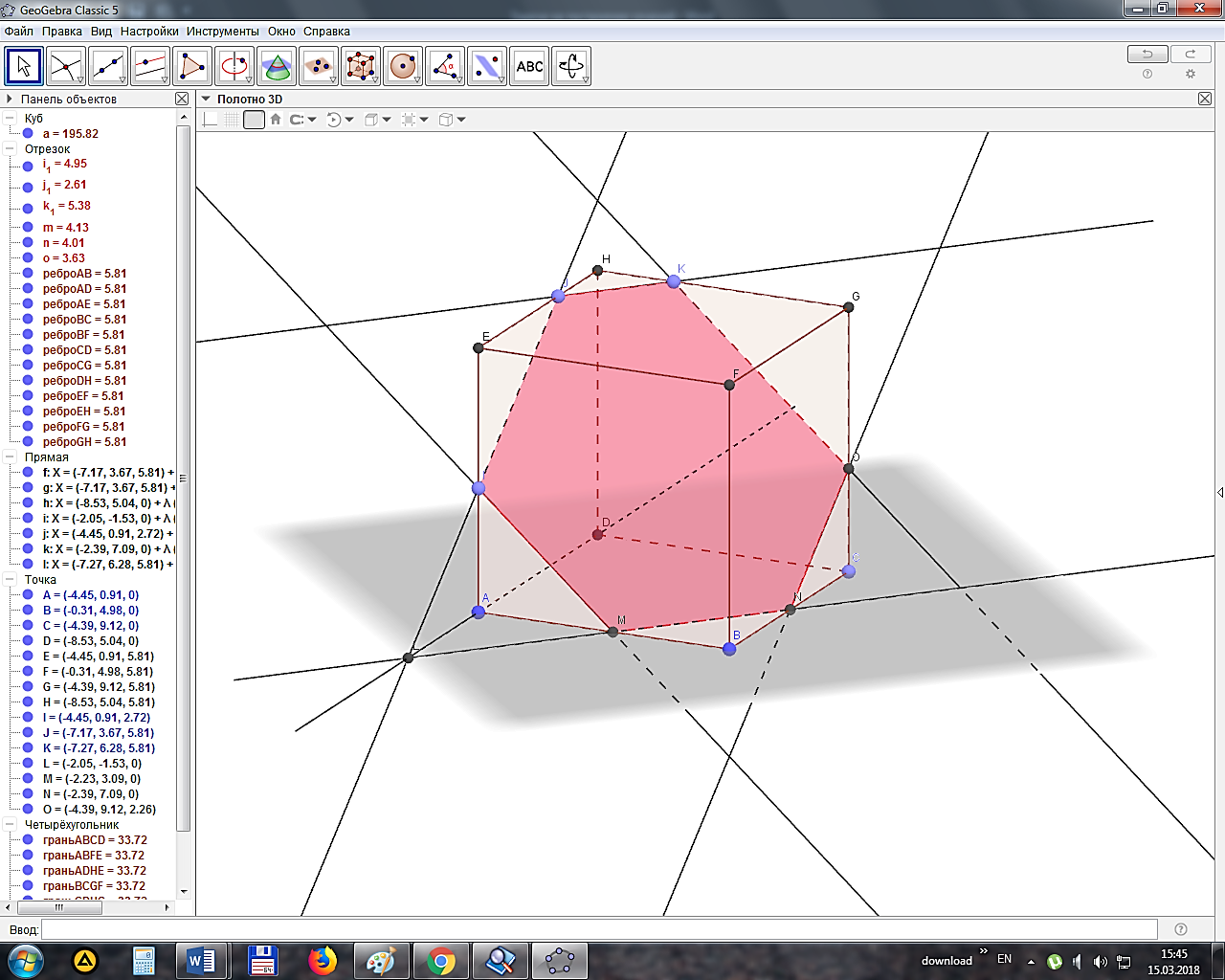
На ребрах параллелепипеда даны три точки A, B, C. Построить сечение параллелепипеда плоскостью ABC (рис. 4).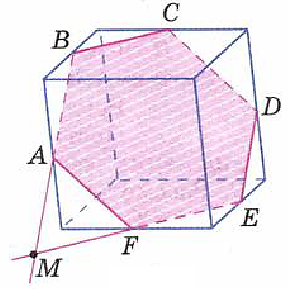

При построении сечений параллелепипеда следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны. Для создания параллелепипеда требуется использовать инструмент

, а для построения сечения нужно выполнять действия аналогичные тем, что использовались в задаче 1.
Список используемых источников

1. Визуализация с помощью Mathematica [Электронный ресурс]. – Режим доступа : https://edunow.su/site/content/personal_blogs/vizualizaciya-s-pomosh-yu-mathematica
2. Основные правила построения изображений [Электронный ресурс]Режим доступа : http://www.myshared.ru/slide/661224/
3. Канин, Е. С. Учебные математические задачи / Е. С. Канин. – Киров: Изд-во ВятГГУ, 2013. – 154 с.
4. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студентов физ.-мат. фак. пед. институтов / Cост. Ю. М. Колягин, В. А. Оганесян, В. Я. Саннинский, Г. Л. Луканкин. – М.: Просвещение, 2011. – 462 с.
5. Mathematica [Электронный ресурс]. – Режим доступа : https://ru.wikipedia.org/wiki/Mathematica

-82%

Источник: videouroki.net

ПРИМЕНЕНИЕ GEOGEBRA ПРИ ПОСТРОЕНИИ СЕЧЕНИЙ
презентация к уроку по геометрии (10, 11 класс)

Условие задачи: На ребрах AB, BC, CD тетраэдра DABC отмечены точки M, N, P. Построить сечение тетраэдра плоскостью MNP.

Откроем программу GeoGebra . В меню Вид выберем Полотно 3D (Полотно 2D можно закрыть) С помощью инструмента создадим тетраэдр DABC. С помощью инструмента на ребрах AB, BC, CD тетраэдра DABC отметим точки M, N, P (переименовать точку можно выделив ее и вызывая контекстное меню правой кнопкой мыши, выбрать соответствующий пункт).

Построим прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E, которая и будет второй общей точкой плоскостей MNP и ABC. Для этого выбрав инструмент нужно щелкнуть поочерёдно по точкам N, P и B, C и с помощью инструмента отметить точку E – точку пересечения прямых NP и BC.

Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро AC в некоторой точке Q. Проведём прямую ME выбрав инструмент и щелкнув поочерёдно по точкам M, E. С помощью инструмента отметим точку Q – точку пересечения прямой ME и ребра AC. Четырёхугольник МNPQ – искомое сечение. Выделим его, используя инструмент поочерёдно щелкая по точками M, N, P, Q, M.

Дважды щелкнув по объектам Tetrahedron и Многоугольник можно вызвать контекстное меню с настройками, в которых можно выбрать цвет заливки и прозрачность соответствующего объекта.

Соблюдение принципа наглядности Экономия времени урока на построение Легкость в использовании Возможность проверки правильности построений Возможность рассмотрения фигур в разных проекциях Преимущества использования GeoGebra на уроках математики

При изучении стереометрии в старших классах, программа может стать незаменимым помощником. Особую трудность у учеников вызывает тема построение сечений. На начальном этапе с помощью GeoGebra можно решить ряд задач, чтобы ученики поняли суть построения сечений и в дальнейшем могли решать задачи без помощи программы, имея основные навыки построения.

По теме: методические разработки, презентации и конспекты

Зачет по теме: Построение сечений. 10 классКонтрольная работа по теме: Тетраэдр и параллелепипед. Построение сечений. 10 класс

Предлагаю для учащихся 10 класса зачет и контрольную работу к учебнику под ред Атанасяна.

Задачи по темам «построение простых разрезов и аксонометрической проекции»,»пересечение тел вращения», «построение сечений фигур фронтально-проецирующей плоскостью» и примеры решения

Эти задания содержат темы «построение простых разрезов и аксонометрической проекции»,»пересечение тел вращения», «построение сечений фигур фронтально-проецирующей плоскостью» а так же примеры их.

«Построение сечений куба и пирамиды. Вычисление площадей полученных сечений»

Интегрированный урок математики и информатики в 10-м классе по теме: «Построение сечений куба и пирамиды. Вычисление площадей полученных сечений»Тип урока: Урок совершенствования знаний, умений и навы.

Технологическая карта урока-семинара по геометрии в 10 классе с применением ИКТ-технологии на тему Построение сечений

Технологическая карта урока-семинара по геометрии в 10 классе с применением ИКТ-технологии на тему Построение сечений.

4. Построения сечений многогранников в Geogebra

Лабораторная работа №4. «Построения сечений многогранников» в интегрированной геометрической среде Geogebra посвящена вопросам построения многогранников, методу следов для построения сечений.

Урок геометрии в 11 классе с применением информационных компьютерных технологий «Построение сечений призмы».

Урок геометрии в 11 классе с применением информационных компьютерных технологий «Построение сечений призмы».

Построение сечений тетраэдра и параллелепипеда с использованием GeoGebra

Урок разработан с использование программы GeoGebra, что способствует большей наглядности и лучше позволяет понять тему «ПОСТРОЕНИЕ СЕЧЕНИЙ тетраэдра и параллелепипедаhttps://nsportal.ru/shkola/geometriya/library/2021/09/19/primenenie-geogebra-pri-postroenii-secheniy» target=»_blank»]nsportal.ru[/mask_link]

Конструктор сечений

Яндекс.Браузер — быстрый браузер с защитой от мошенников и вредоносных сайтов.

• Windows 7
• Windows Vista
• Windows XP

Тип лицензии:
Демо-версия

Языки: Русский

Конструктор сечений – программа для создания и обработки стандартных профильных сечений. Типы поддерживаемых профилей: металлические пластины, швеллер, двутавр, трубы и уголки.

Функционал программы Конструктор сечений:

• На основании типа сечения определяются геометрические характеристики, моменты инерции и сопротивления. Расчет моментов проводится относительно осей и при свободном кручении элемента.
• Вычисление напряжений в двух плоскостях.
• Графическое представление в виде эпюры.
• Сборка сечений посредством присоединения узлов.
• Автоматическое создание отчетного документа типа RTF – Word.
• Выгрузка данных в Structure CAD или Кристалл 2.1+.

В освоении Конструктора сечений поможет профессионально составленная справочная система. Практическое применение программы: строительно-проектная отрасль и технические ВУЗы.

Источник: www.softsalad.ru