Числа Фибоначчи применяются самыми разнообразными способами в различных сферах человеческой деятельности. В частности, на их основе строят всевозможные геометрические разметки графиков котировок, помогающих в анализе и прогнозировании. Один из самых сложных, а потому и экзотических инструментов Фибоначчи – спираль, построить которую можно двумя способами.
Чтобы построить классическую идеальную спираль Фибоначчи, надо построить определенную последовательность квадратов, внутрь которых вписать по дуге радиусом в сторону квадрата в 90°, соединяющей две противоположные стороны. Эти квадраты должны иметь по одной общей стороне – такая структура формируется так:
- строятся два равных квадрата с одной общей стороной, длина которой принимается за 1 (получается прямоугольник 1х2, поделенный поперек пополам);
- затем на длинной стороне достраивается новый квадрат 2х2, в результате чего внешние контуры образованной фигуры стали прямоугольником размером 2х3;
- процесс построения продолжается, при этом для нового построения выбираются только те длинные стороны, которые находятся от предыдущей длинной стороны, на которой происходило предшествующее построение, только в направлении по часовой стрелке или против нее.

Как начертить золотую спираль
Рисунок 1. Вот так можно построить спираль Фибоначчи из двух симметричных идеальных.
А другой вариант, называющийся спиралью «золотого сечения», «фи» или логарифмической, тоже предполагает подобное рисование дуги четверти окружности внутри квадратов, но их построение происходит так:
- строится прямоугольник, стороны которого соотносятся как «золотое сечение»;
- путем деления поперек, внутри этого прямоугольника формируется квадрат, а также прямоугольник с меньшими размерами, но с длинами сторон, тоже соотносящимися как «фи»;
- процесс продолжается, и каждый новый квадрат должен примыкать к новой стороне, последовательность которых меняется либо по часовой, либо против часовой стрелки (например, по часовой стрелке – к верхней, к правой, к нижней, к левой, к верхней и т. д.), т. е. спиралеобразно.
Разница между логарифмической и идеальной спиралями Фибоначчи, помимо построения, заключается в наличии у второй начальной точки. Всех остальных концов ни у той, ни у другой спиралей нет, т. е.:
- идеальная спираль Фибоначчи бесконечна в конец, т. е. является лучом;
- логарифмическая спираль бесконечна в обе стороны – ни начальной, ни конечной точек у нее нет.
Естественное построение спирали Фибоначчи
Природа уже давно смогла создавать самые причудливые закономерности. Не стала исключением и спираль Фибоначчи, встречающаяся повсеместно и в самых разных масштабах. Например, семена подсолнечника и чешуйки шишек располагаются именно по траекториям, очень точно похожим на спирали Фибоначчи. А еще такие траектории образуют рукава спиральных звездных скоплений – галактик.
Спираль Фибоначчи / Как рисовать
При пролете комет вблизи Солнца становится видимым их хвост, состоящий из покидающего их поверхности вещества. Этот хвост имеет траекторию, близкую к логарифмической спирали Фибоначчи. По ней же описывает траекторию нитей в сети при ее плетении паук Epeira. А еще спираль Фибоначчи можно наблюдать в строении:
- тел морских коньков;
- раковин улиток;
- рогов некоторых копытных;
- океанических волн;
- облачности циклона;
- согнутых пальцев руки;
- сохнущего листа растения.
Как построить спираль Фибоначчи самостоятельно
Понадобиться это может, например, в анализе рынка с использованием волновых теорий. В этом случае каждый виток спирали указывает на временные координаты вероятных рыночных состояний. Проще всего использовать для построения спирали Фибоначчи в терминале какой-нибудь индикатор, например, FX5_FiboSpiral.

Рисунок 2. Построение спирали Фибоначчи в MetaTrader можно выполнить индикатором , FX5_FiboSpiral.
На графике (рис. 2) его алгоритм определяет наиболее оптимальную зону для начала построения – она обозначена синим квадратом. Из одного из его углов начинает расходиться кривая, у которой угол искривления последовательно и непрерывно увеличивается, стремясь к 180°. Получающаяся спираль Фибоначчи – идеальная.
Если изменять масштаб графика котировки, то одновременно будут меняться и пропорции между вертикальными и горизонтальными размерами спирали. В результате можно получить спиральную фигуру любой овальности, в том числе, круглой.
Для настройки индикатора построения спирали Фибоначчи используются три переменные:
- Accurity – степень сглаживания угловатости спирали (чем больше значение, тем длиннее будут аппроксимирующие отрезки и тем больше будет угол между ними);
- GoldenSpiral_Cycle – коэффициент временной цикличности витков (чем больше значение, тем дальше от предыдущего будет рисоваться следующий виток);
- Radius – относительный радиус начального витка (чем больше значение, тем на большем расстоянии от центра начнет рисоваться первый виток).
При правильных настройках витки спирали будут очень точно указывать на несколько экстремумов в ближайшем прошлом. Тогда подход котировки к очередному витку идеальной спирали Фибоначчи, построенной FX5_Fibo_Spiral, служит признаком формирования очередного экстремума:
- если до этого котировка преимущественно снижалась, тогда образуется минимум, т. е. завершение нисходящего тренда, поэтому целесообразно войти в рынок длинной позиций;
- если до этого котировка преимущественно росла, тогда образуется максимум, т. е. завершение восходящего тренда, поэтому целесообразно войти в рынок короткой позицией.
Источник: forexxx4all.ru
Fibonacci Tiles and Spiral
Fibonacci numbers are series of numbers, or a sequence, where every next number is the sum of the previous two numbers. The sequence starts with 0 and the next number is 1 . The third number is also 1 because 0 + 1 = 1 . The numbers following that are 1 + 1 = 2 , 1 + 2 = 3 , and so on. For the first 10 numbers in the sequence, we have:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Because of how each number in the sequence is the sum of the previous two, the Fibonacci numbers are sometimes used to represent natural growth rates.
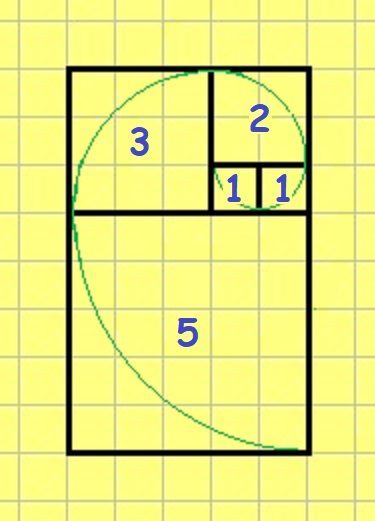
In the picture above, squares are drawn with sides that are the length of a Fibonacci number. You see that squares are tiled together perfectly in a spiral pattern starting at the smallest square and then moving out in a counter-clockwise direction. Also, an actual spiral is inscribed within the squares using quarter-circle arcs that are the radius of the Fibonacci number for that square. As more squares and arcs are drawn, the drawing surface will fill “naturally”. Each larger square will tile next to the smaller ones without any gaps and the spiral will grow smoothly with a natural bend.
Generate Fibonacci Numbers
A simple way to show the Fibonacci numbers is to generate them in a loop and then show each number as the game score. Here’s a way to show the first 10 numbers:
let f0 = 0 let f1 = 1 let fibo = 0 for (let i = 0; i
Fibonacci Tiling
The Fibonacci tiles are sprites that have square images. The square image sides are the length of the current Fibonacci number. As each square sprite is created, they are placed next to the previous square in a counter-clockwise pattern.
To do this, we use a 4 step rotation sequence that places the new squares next to the previous square in the right location.
The current rotation step is kept in the rotation variable. A complete rotation happens in 4 steps so the rotation variable is reset to 0 after the square sprite is placed in rotation step 4 .
We have to remember the location of each previous sprite so that the next sprite is placed at the proper location. The previous sprite is saved in the fibSprite0 variable. The first square is a “virtual” square since the length of its sides is 0 .
The sequence is run for 14 squares and a different color is used for each square.
let fibSprite: Sprite = null let fibSquare: Image = null let rotate = 0 let clr = 1 let repeat = 14 let f = 0 let f0 = 0 let f1 = 1 let fibSprite0 = sprites.create(img`.`, 0) fibSprite0.top += 20 game.onUpdateInterval(1000, function () < if (repeat >0) < f0 = f1 f1 = f f = f1 + f0 info.setScore(f) repeat += -1 fibSquare = image.create(f, f) fibSquare.fillRect(0, 0, f, f, clr) clr += 1 fibSprite = sprites.create(fibSquare, 0) if (rotate == 0) < fibSprite.top = fibSprite0.bottom fibSprite.left = fibSprite0.left rotate += 1 >else if (rotate == 1) < fibSprite.bottom = fibSprite0.bottom fibSprite.left = fibSprite0.right rotate += 1 >else if (rotate == 2) < fibSprite.bottom = fibSprite0.top fibSprite.right = fibSprite0.right rotate += 1 >else if (rotate == 3) < fibSprite.top = fibSprite0.top fibSprite.right = fibSprite0.left rotate = 0 >fibSprite0 = fibSprite > >)
Fibonacci Spiral
We can add a Fibonacci spiral to the squares in the program above using a function to draw arcs. The function can use the current value for the Fibonacci number as the arc radius. It follows the rotation sequence to know the direction to draw the arc. The arcs are drawn in the images for the squares using random dots that paint the arc line.
let f = 0 let x = 0 let y = 0 let rotate = 0 let fibSquare: Image = null function drawArc() < // draw a circle arc using random dots! for (let i = 0; i < 100000; i++) < x = randint(0, f) y = randint(0, f) // test if the point will draw the circle if (x * x + y * y >= (f — 1) ** 2 x * x + y * y < (f + 1) ** 2) < if (rotate == 0) < x = f — x y = f — y >else if (rotate == 1) < x = f — x >else if (rotate == 3) < y = f — y >fibSquare.setPixel(x, y, 1) > > > drawArc()
Add the drawArc function to the previous program and call the the function just before updating the previous Fibonacci sprite:
let fibSprite0: Sprite = null let fibSprite: Sprite = null function drawArc() <> drawArc() fibSprite0 = fibSprite
Pan the View
The squares and the spiral will eventually fill outside the view of the screen. To see all of the squares you can add code to scroll the screen view. The following code uses the arrow buttons to change the camera view center in order to scroll the screen view in 4 directions.
let cx = scene.screenWidth() / 2 let cy = scene.screenHeight() / 2 controller.left.onEvent(ControllerButtonEvent.Pressed, function () < cx += -20 scene.centerCameraAt(cx, cy) >) controller.right.onEvent(ControllerButtonEvent.Pressed, function () < cx += 20 scene.centerCameraAt(cx, cy) >) controller.up.onEvent(ControllerButtonEvent.Pressed, function () < cy += -15 scene.centerCameraAt(cx, cy) >) controller.down.onEvent(ControllerButtonEvent.Pressed, function () < cy += 15 scene.centerCameraAt(cx, cy) >)
Полная программа
The complete program contains the tile drawing code, the arc function to draw the spiral, and the screen panning code.
let fibSprite: Sprite = null let fibSquare: Image = null let rotate = 0 let x = 0 let y = 0 let clr = 1 let repeat = 14 let f = 0 let f0 = 0 let f1 = 1 let fibSprite0 = sprites.create(img`.`, 0) let cx = scene.screenWidth() / 2 let cy = scene.screenHeight() / 2 fibSprite0.top += 20 game.onUpdateInterval(1000, function () < if (repeat >0) < f0 = f1 f1 = f f = f1 + f0 info.setScore(f) repeat += -1 fibSquare = image.create(f, f) fibSquare.fillRect(0, 0, f, f, clr) clr += 1 fibSprite = sprites.create(fibSquare, 0) if (rotate == 0) < fibSprite.top = fibSprite0.bottom fibSprite.left = fibSprite0.left rotate += 1 >else if (rotate == 1) < fibSprite.bottom = fibSprite0.bottom fibSprite.left = fibSprite0.right rotate += 1 >else if (rotate == 2) < fibSprite.bottom = fibSprite0.top fibSprite.right = fibSprite0.right rotate += 1 >else if (rotate == 3) < fibSprite.top = fibSprite0.top fibSprite.right = fibSprite0.left rotate = 0 >drawArc() fibSprite0 = fibSprite > >) function drawArc() < // draw a circle arc using random dots! for (let i = 0; i < 100000; i++) < x = randint(0, f) y = randint(0, f) // test if the point will draw the circle if (x * x + y * y >= (f — 1) ** 2 x * x + y * y < (f + 1) ** 2) < if (rotate == 0) < x = f — x y = f — y >else if (rotate == 1) < x = f — x >else if (rotate == 3) < y = f — y >fibSquare.setPixel(x, y, 1) > > > controller.left.onEvent(ControllerButtonEvent.Pressed, function () < cx += -20 scene.centerCameraAt(cx, cy) >) controller.right.onEvent(ControllerButtonEvent.Pressed, function () < cx += 20 scene.centerCameraAt(cx, cy) >) controller.up.onEvent(ControllerButtonEvent.Pressed, function () < cy += -15 scene.centerCameraAt(cx, cy) >) controller.down.onEvent(ControllerButtonEvent.Pressed, function () < cy += 15 scene.centerCameraAt(cx, cy) >)
Источник: arcade.makecode.com
Золотая спираль Фибоначчи в Timing Solution
Золотая спираль Фибоначчи — это один из интересных инструментов графического технического анализа; используется он не так рьяно, ввиду сложности построения и реализации спирали в программах. Но, на мой взгляд, этот инструмент, безусловно, заслуживает внимания и мы рассмотрим, как с этим работают в Timing Solution.
Спираль эта имеет логарифметический характер (ее так и называют — логарифметической спиралью) и раскручивается она, исходя из пропорций, в основе которых лежит то самое легендарное число 1,618: «золотые сечение», «число Фи» и т.д. Собственно поэтому, спираль называется «золотой».

Немного истории
Числовая последовательность, лежащая в основе спирали, была описана и исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая, что: изначально есть новорожденная пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?
В данных идеальных условиях, если исключить голод, болезни и прочие негативные факторы, к концу года в вольере будет насчитываться 233 кролика. Вроде все просто, но данная задачка она открыла окно в совершенно иную область исследований.
Оказалось, что в числовой последовательно размножения кроликов соотношение каждого нового числа к предыдущему стремится к 1,618. Да, пропорция получается не идеальная, особенно на первых нескольких коленах, но по мере увеличения масштаба ряда она становится всё очевиднее.

При чем здесь, собственно, кролики? Решением этой задачи Фибоначчи экспериментально доказал, что «золотое сечение» является не просто «выдумкой» математиков прошлого — оно действительно работает в биологических и эволюционных процессах. В итоге аналогичные закономерности были найдены практически везде, т.е. в космосе, геологии и биологии, но для нас наибольший интерес будет представлять «идеальная раковина моллюска», которая разворачивается по спирали и соотношения которой подчиняются пропорциям ряда Фибоначчи.

От кроликов к финансовым рынкам
Если число 1,618 является неким универсальным числом, работающим в природных процессах, резонно предположить — нельзя ли ряд Фибоначчи использовать в прогнозировании такого эволюционного процесса, как финансовые рынки? О том, что такие попытки предпринимались неоднократно, и в самых различных формах, знает любой трейдер, не будем углубляться в дебри. Остановимся на такой редкой разновидности, как «золотая спираль» (ясное дело, золотой она называется только потому, что в основе ее построения лежит принцип «золотого сечения»). На Западе этот инструмент называется также Fibonacci Vortex. Спираль встречается в программах по анализу рынку, но довольно редко — я знаю что это есть в Wave59; в Timing Solution же данный инструмент также присутствует.
Находится инструмент построения золотой спирали Фибоначчи здесь, в панели Сharting Tools — Figures — Spiral:

Чтобы построить спираль, вам нужно будет выбрать, на графике котировок, три якорные точки, на которых и будет базироваться спираль. По сути, щелкнуть три раза по диаграмме — и спираль построена. Первым щелчком вы выбираете центр спирали; вторым щелчком радиус и третьим — ее период. Самый главный (и пока еще дискутируемый) вопрос — где именно должны располагаться эти самые якорные точки?
На мой взгляд, центр спирали — это всегда локальный экстремум графика котировок на текущий момент: топ или минимум. Это будет первая точка, здесь вы ставите первый «якорь». Вторая якорная точка — ближайший контрэкстремум справа от нее. Третья — контрэкстремум уже слева от центра. Таким образом, если мы строим спираль от топа, то щелкаем вначале по топу, затем справа от нее по ближайшему дауну, и далее — слева от топа, по ближайшему дауну. Вот как эти предполагаемые якорные точки выглядят на графике:

Активируем на панели Сharting Tools нашу спираль, последовательно щелкаем в этих трех местах, получаем вот это:

Обратите внимание, что мы работаем не только со спиральными линиями, но и с производными от них (вертикальными и горизонтальными линиями от боков спирали). Вот здесь мы построили уровни поддержки/сопротивления от «завитушек» спирали (уровни 1087, 1174, 1270), и эти горизонтальные линии-уровни хорошо работают:

Точно также мы можем строить у вертикальные линии от боков спирали — они покажут, где по времени следует ждать формирования очередного максимума или минимума: так сказать, предполагаемая временная отметка перелома рынка. Разумеется, спираль необходимо сочетать с другими методиками прогноза в программе, например, с циклическим анализом.
Дополнительную информацию вы можете почерпнуть здесь, видео Юрия Шраменко на английском языке: http://www.timingsolution.com/Yuri/ — Spiral examples
Как это работает?
Конечно, мы задаемся вопросом — как это вообще работает? Вероятно, есть некоторые «вселенские» закономерности, которые проявляются не только в природных процессах, но и на финансовых рынках. Конечно, Леонардо Пизанский и предположить не мог, что через сотни лет его труды будут применяться для спекулятивных операций, но в этом нет ничего удивительного.
Движение финансовых рынков — дело рук обычных живых людей, т.е. цены определяются эмоциональной реакцией всех трейдеров и инвесторов на происходящие события, а поведение толпы людей немногим отличается от поведения группы кроликов; как уже было неоднократно установлено социологами, поведение толпы также можно описать при помощи волн и золотого сечения.
Судя по всему, причины этого явления следует искать в биологической плоскости, поскольку человеческий социум – это, прежде всего, популяция, т.е. один человек может вести себя странно и непредсказуемо, но в масштабе планеты или страны поведение населения подчиняется определенным законам.
И кстати, о числе ФИ, 1,618. Оно названо не в честь Фибоначчи, как это может показаться. Оно было известно еще в древности (Фибоначчи просто нашел ему практическое применение, вывел числовой ряд, исходя из этого числа). На самом же деле, данный коэффициент назван в честь древнегреческого архитектора Фидия, который активно его использовал при строительстве сооружений, в частности, пирамид:
Источник: timing-solution.livejournal.com