На протяжении всей истории углы были измерены в разных единицах. Они известны как угловые единицы, при этом самыми современными единицами измерения являются градус (°), радиан (рад) и градиан (град), хотя многие другие использовались на протяжении всей истории. Цель этой страницы — собрать воедино другие концепции, относящиеся к угловой единице, где могут быть предоставлены дополнительные пояснения.
Измерение углов в целом
Размер геометрического угла обычно характеризуется величиной наименьшего поворота, который переводит один из лучей в другой. Углы, имеющие одинаковый размер, называются равными, конгруэнтными или равными по размеру.
В некоторых контекстах, таких как определение точки на окружности или описание ориентации объекта в двух измерениях относительно исходной ориентации, углы, которые отличаются точным кратным полному повороту эффективно эквивалентны. В других контекстах, таких как определение точки на кривой спирали или описание совокупного поворота объекта в двух измерениях относительно исходной ориентации, углы, которые отличаются ненулевым кратным полному обороту не эквивалентны.
Программирование MakeRobots. Занятие №7. Прерывания, энкодеры, дальномер
Чтобы измерить угол θ , рисуется дуга окружности с центром в вершине угла (например, с помощью пары циркуля ). Отношение длины s дуги к радиусу r круга — это мера угла в радианах.
Мера угла в другом угловом Затем получается единица измерения путем умножения ее меры в радианах на коэффициент масштабирования k / 2π, где k — это величина полного поворота в выбранной единице (например, 360 для градусов или 400 для градианы ):
Определенное таким образом значение θ не зависит от размера круга: если длина радиус изменяется, затем длина дуги изменяется в той же пропорции, поэтому отношение s / r не изменяется. (Доказательство. Формулу выше можно переписать как k = θr / s. Один оборот, для которого θ = n единиц, соответствует дуге, равной длине окружности окружности, которая равна 2πr, поэтому s = 2πr. Подстановка n вместо θ и 2πr вместо s в формуле дает k = nr / 2πr = n / 2π.)
В частности, величина угла в радианах также может интерпретироваться как дуга длина соответствующей единичной окружности:
Постулат сложения углов
Постулат сложения углов утверждает, что если B находится внутри угла AOC, то
m ∠ AOC = m ∠ AOB + m ∠ BOC
Мера угла AOC — это сумма измерения угла AOB и меры угла BOC. В этом постулате не имеет значения, в каких единицах измеряется угол — до тех пор, пока каждый угол измеряется в одной и той же единице.
Единицы
Определение 1 радиана
Один радиан — это угол, образованный дугой окружности, имеющей ту же длину, что и радиус окружности. Радиан — это производная величина углового измерения в системе SI. По определению, это безразмерный, хотя он может быть указан как рад, чтобы избежать двусмысленности. Углы, измеренные в градусах, отображаются символом °. Подразделения градуса: минута (символ ‘, 1’ = 1/60 °) и секунда . Угол 360 ° соответствует углу, образуемому полным кругом, и равен 2π радианам или 400 градусам.
Размеры в AutoCAD. Как поставить, изменить, масштабировать размеры в Автокад
Другие единицы измерения углов перечислены в следующей таблице. Эти единицы определены таким образом, что число витков эквивалентно полному кругу.
| поворот | 1 | 360 ° | Поворот, также цикл, полный круг, вращение и вращение — это полное круговое движение или измерение (чтобы вернуться в ту же точку) с помощью круга или эллипса. Оборот обозначается сокращенно τ, cyc, rev или rot в зависимости от применения. Символ τ также может использоваться как математическая константа для представления 2π радиан. |
| Умножение на π | 2 | 180 ° | Функция кратного π (MULπ) реализована в научном калькуляторе RPN WP 43S. См. Также: Рекомендуемые операции IEEE 754 |
| Квадрант | 4 | 90 ° | Один квадрант также известен как прямой угол. Квадрант — это единица измерения, используемая в Элементах Евклида. В немецком языке этот символ использовался для обозначения квадранта. |
| Секстант | 6 | 60 ° | Секстант был единицей, используемой вавилонянами. Градус, угловая минута и секунда дуги — шестидесятеричные субъединицы из вавилонского подразделения. Особенно легко строить с помощью линейки и циркуля. |
| Радиан | 2π | 57°17′ | Радиан определяется длиной окружности, равной радиусу окружности. |
| Гексаконтада | 60 | 6° | Гексаконтада — это единица измерения, используемая Эратосфеном. |
| двоичным градусом | 256 | 1 ° 33’45 « | двоичным градусом, также известный как двоичный радиан (или Брэд). Двоичная степень используется в вычислениях, чтобы угол можно было эффективно представить в одном байте (хотя и с ограниченной точностью). Другие меры угла, используемого при вычислении, может быть основано на делении одного целого витка на 2 равные части для других значений n. |
| Степень | 360 | 1° | Одно из преимуществ этой старой шестидесятеричной субъединицы состоит в том, что углы, общие для простой геометрии, измеряются как целое число градусов. Доли градуса могут быть записаны в обычном десятичном представлении (например, 3,5 ° для трех с половиной градусов), но «минута» и «секунда» шестидесятеричной части Система «градус-минута-секунда» также используется, особенно для географических координат и в астрономии и баллистике |
| Град | 400 | 0 ° 54 ′ | Град, также называемый градусом, градусом, или гон. прямой угол — 100 градусов. Это десятичная единица квадранта. километр исторически определялся как сантиметров градус дуги вдоль меридиана Земли, поэтому километр является десятичным аналогом шестидесятичной запятой. морская миля. Град используется в основном в триангуляции. |
| Угловая минута | 21,600 | 0 ° 1 ′ | Угловая минута (или MOA, угловая минута или просто минута) составляет 1/60 градуса. морская миля исторически определялась как угловая минута вдоль большого круга Земли. |
| Угловая секунда | 1,296000 | 0 ° 0′1 ″ | Угловая секунда (или угловая секунда, или просто секунда) составляет 1/60 угловой минуты и 1/3600 градуса. |
Эквивалентные дескрипторы времени
В астрономии, прямое восхождение и склонение обычно измеряются в угловых единицах, выраженных во времени, исходя из 24-часового рабочего дня.
| h | 15 ° | ⁄12 | ⁄24 | |
| m | 0 ° 15 ‘ | ⁄720 | ⁄1,440 | ⁄60час |
| s | 0 ° 0’15 « | ⁄43200 | ⁄86,400 | ⁄60минута |
Другие дескрипторы
- Tau, количество радиан в одном обороте (1 оборот = τ рад), τ = 2π.
- Chi, старое китайское измерение угла.
- Часть диаметра (n = 376,99. ): Часть диаметра (иногда используемая в исламской математике) составляет 1/60 радиана. Одна «часть диаметра» составляет приблизительно 0,95493 °. На оборот приходится около 376,991 частей диаметра.
- Миллирадиан и производные определения: Истинный миллирадиан определяется одной тысячной радиана, что означает, что поворот на один оборот будет равен точно 2000π мил (или приблизительно 6283,185 мил), и почти все прицелы для огнестрельного оружия откалиброваны в соответствии с этим определением. Кроме того, есть три других производных определения, используемых для артиллерии и навигации, которые приблизительно равны миллирадиану. В этих трех других определениях один оборот составляет ровно 6000, 6300 или 6400 мил, что соответствует диапазону от 0,05625 до 0,06 градуса (от 3,375 до 3,6 минут). Для сравнения, истинный миллирадиан составляет приблизительно 0,05729578 градуса (3,43775 минуты). Один «NATO mil» определяется как 1/6400 круга. Как и в случае с истинным миллирадианом, каждое из других определений использует полезное свойство миллирадиана, то есть то, что значение одного миллирадиана приблизительно равно углу, образуемому шириной 1 метр, если смотреть с расстояния 1 км (2π / 6400 = 0,0009817 … ≈ 1/1000).
- Ахнам и зам. В старой Аравии поворот был разделен на 32 акнама, и каждый ахнам был подразделен на 7 зам, так что поворот равен 224 зам.
Положительные и отрицательные углы
Хотя определение измерения угла не поддерживает концепцию отрицательного угла, часто бывает полезно ввести соглашение, которое позволяет положительным и отрицательным угловым значениям представлять ориентацию и повороты в противоположных направлениях относительно некоторой ссылки.
В двумерной декартовой системе координат угол обычно определяется двумя его сторонами с вершиной в начале координат. Начальная сторона находится на положительной оси x, в то время как другая сторона (т. Е. Конечная сторона) определяется мерой от начальной стороны в радианах, градусах или поворотах. Обычно положительные углы представляют собой повороты к положительной оси y, а отрицательные углы представляют повороты к отрицательной оси y. Когда декартовы координаты представлены стандартным положением, определяемым осью x вправо и осью y вверх, положительные повороты равны против часовой стрелки, а отрицательные повороты равны по часовой стрелке.
Во многих контекстах угол -θ фактически эквивалентен углу «один полный оборот минус θ». Например, ориентация, представленная как -45 °, фактически эквивалентна ориентации, представленной как 360 ° — 45 ° или 315 °. Однако поворот на -45 ° не будет таким же, как поворот на 315 °.
В трехмерной геометрии «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно быть определено относительно некоторой ссылки, которая обычно является вектором проходящий через вершину угла и перпендикулярный плоскости, в которой лежат лучи угла.
В навигации, пеленг измеряются относительно севера. Условно, если смотреть сверху, угол пеленга по часовой стрелке положительный, поэтому пеленг 45 ° соответствует ориентации на северо-восток. Отрицательные пеленги не используются в навигации, поэтому ориентация на северо-запад соответствует пеленгу 315 °.
Альтернативные способы измерения размера угла
Существует несколько альтернатив измерению размера угла с помощью соответствующего угла поворота. Уровень уклона или градиента равен касательной угла или иногда (редко) синусу . Градиенты часто выражаются в процентах. Для очень малых значений (менее 5%) крутизна наклона приблизительно равна величине угла в радианах.
В рациональной геометрии расстояние между двумя линиями определяется как квадрат синуса угла между линиями. Поскольку синус угла и синус его дополнительного угла одинаковы, любой угол поворота, который отображает одну из линий в другую, приводит к одинаковому значению разброса между линиями.
Астрономические приближения
Астрономы измеряют угловое расстояние между объектами в градусах от точки наблюдения.
- 0,5 ° приблизительно соответствует ширине солнца или луны.
- 1 ° приблизительно соответствует ширине мизинца на расстоянии вытянутой руки.
- 10 ° приблизительно соответствует ширине закрытого кулак на расстоянии вытянутой руки.
- 20 ° — это примерно ширина размаха руки на длине руки.
Эти размеры явно зависят от индивидуального объекта, и вышеизложенное следует рассматривать как грубое практическое правило только приблизительные значения.
Измерения, не являющиеся угловыми единицами
Не все угловые измерения являются угловыми единицами, для углового измерения определенно соблюдается постулат сложения углов.
Некоторые измерения углов, для которых постулат сложения углов не выполняется, включают:
Примечания
См. Также
- Угловой ускорение
- Угловой диаметр
- Десятичные градусы
- Телесный угол
Источник: alphapedia.ru
В чем измеряется угловое ускорение? Пример задачи на вращение
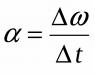
Движение по окружности или вращательное перемещение твердых тел является одним из важных процессов, который изучают разделы физики — динамика и кинематика. Данную статью посвятим рассмотрению вопроса, в чем измеряется угловое ускорение, которое появляется во время вращения тел.
Понятие об угловом ускорении
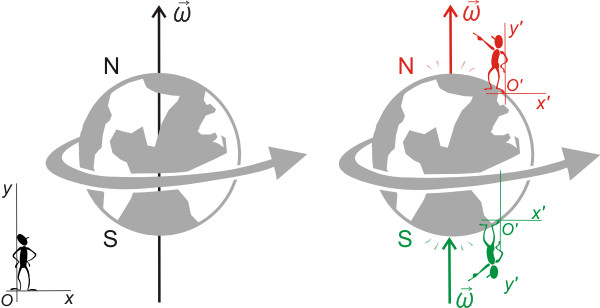
Очевидно, что прежде чем давать ответ на вопрос, в чем измеряется угловое ускорение в физике, следует познакомиться с самим понятием.
В механике линейного движения ускорение играет роль меры быстроты изменения скорости и вводится в физику через второй закон Ньютона. В случае вращательного движения существует аналогичная линейному ускорению величина, которая называется ускорением угловым. Формула для его определения записывается в виде:
То есть угловое ускорение α является первой производной угловой скорости ω по времени. Так, если скорость во время вращения не изменяется, то ускорение будет равно нулю. Если же скорость линейно зависит от времени, например, увеличивается постоянно, то ускорение α примет постоянное ненулевое положительное значение. Отрицательное значение α говорит о том, что система замедляет свое вращение.
Динамика вращения
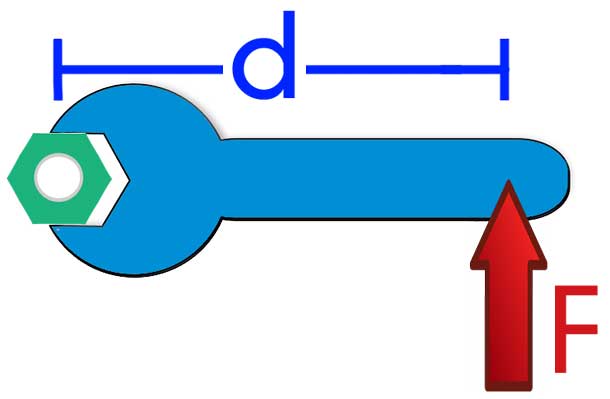
В физике всякое ускорение возникает только тогда, когда существует ненулевая внешняя сила, действующая на тело. В случае движения вращения эта сила заменяется на момент силы M, равный произведению плеча d на модуль силы F. Известное уравнение моментов динамики вращательного перемещения тел записывается в следующем виде:
Здесь I — момент инерции, играющий ту же роль в системе, что и масса во время линейного перемещения. Эта формула позволяет вычислить величину α, а также определить, в чем измеряется угловое ускорение. Имеем:
Измерение угла поворота диска с помощью энкодера и микроконтроллера Atmega16A
Тихонов, П. А. Измерение угла поворота диска с помощью энкодера и микроконтроллера Atmega16A / П. А. Тихонов. — Текст : непосредственный // Молодой ученый. — 2016. — № 5 (109). — С. 82-86. — URL: https://moluch.ru/archive/109/26619/ (дата обращения: 04.07.2023).
В данной статье будет рассмотрен метод измерения угла поворота диска с помощью энкодера и микроконтроллера Atmega16A. Вначале будут рассмотрены общие сведения об энкодерах, их классификация, далее будет рассмотрена непосредственно сама прошивка для микроконтроллера.
Энкодер/преобразователь угловых перемещений — устройство, предназначенное для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота.
Существует несколько видов энкодеров (оптические, резистивные, магнитные, индуктивные, механические), работа каждого вида основана на своём принципе. Для решения данной задачи был выбран оптический энкодер.
Существует два типа оптических энкодеров, а именно: абсолютные и инкрементальные (относительные). Абсолютные энкодеры позволяют в любой момент времени знать текущий угол поворота оси, также после пропадания и восстановления питания. Инкрементальные определяют угол по количеству импульсов.
Простейшим типом инкрементного энкодера является одноканальный энкодер, обычно состоящий из механического прерывателя света, производящего определенное количество прямоугольных или синусоидальных импульсов, при каждом обороте вала. По количеству этих импульсов можно понять, на какой угол повернулся вал.
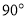
Одноканальный тахометр не позволяет определить направление вращения, поэтому используется только в качестве тахометра и не может быть использован в качестве датчика положения. Поэтому существуют двухканальные энкодеры, которые преодолели эти проблемы путём добавления второго канала, смещенного относительно первого таким образом, что два выходных канала сдвинуты по фазе на . Это позволяет определить, какой канал опережает другой и, следовательно, установить направление вращения. При этом увеличивается разрешение из-за увеличения количества различных состояний с двух (в одноканальном) до четырёх без изменения конструкции.
Для вывода информации об угле, в нашем расположении было четыре 7ми-сегментных дисплея.
Их принцип работы довольно прост. Существуют обозначения для каждого сегмента дисплея: последовательно буквы «A» — «G» и обозначение «DP» для точки. При подаче напряжения на сам ножку питания дисплея, загораются все его сегменты, поэтому, чтобы погасить неиспользуемые, на контакты, соответствующие своему сегменту, необходимо подать напряжение.
Зная это, можно перейти к программе для микроконтроллера.
«A» канал подключён к ножке Int0 микроконтроллера — контакту, отвечающему за внешние прерывания. Прерывание происходит на падающем фронте.
«B» канал подключён к одной из ножек, настроенной как вход.
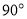
Во время прерывания на Int0, проверяется логическое значение сигнала на канале «B». От этого значения зависит направление поворота (т. к. отставание у канала «B» на ).
В главном цикле программы происходит выполнение функции показа заданного числа: для каждого дисплея определяется цифра, которая должна быть выведена на него, далее, уже для каждого дисплея, в свою очередь, вызывается ещё одна функция, которая отвечает за само отображение цифры на дисплее.
По Int1 происходит прерывание по изменению сигнала. Оно отвечает за показ на дисплее угла/количества тиков.
Формула для преобразования количества тиков в угол следующая:
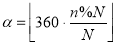
где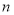 
— текущее количество тиков, 
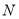— количество тиков на оборот
Код программы на C:
Источник: moluch.ru