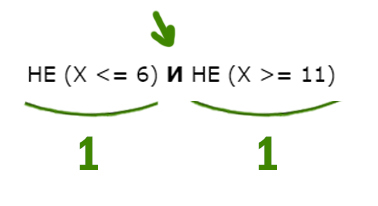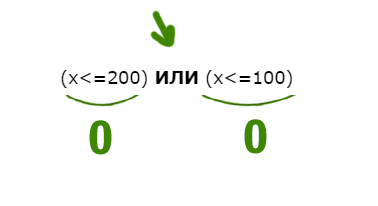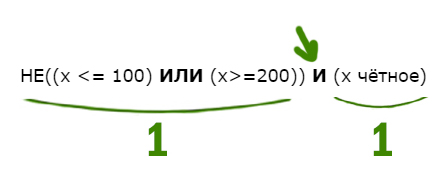Укажите ложное высказывание имя программы может совпадать

Суть: эквивалентность ложна только тогда, когда выражения разные.

Законы алгебры логики

Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.

Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.

Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.

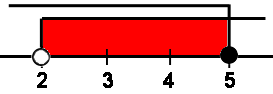
Порядок решения логического выражения

В первую очередь надо учитывать, что порядок задается скобками.

Далее выполняются операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности.

Построение таблиц истинности

Чтобы решить логическое выражение, необходимо построить таблицу истинности, описывающую ВСЕ возможные варианты значений переменных величин. В связи с тем, что мы используем булевы переменные (то есть имеющие только два значения: 0 и 1), количество вариантов легко сосчитать по формуле

M = 2 N ,

где N — число переменных, а M — число строк в результирующей таблице.

Заполнение же значений фактически является последовательным вписыванием в каждой строке двоичных чисел. Для первой строки это будет 0 (00, 000. ), для второй — 1 (01, 001. ), а для последней — числа, состоящего из всех единиц. Выполнение этого несложного правила позволит не только избежать ошибок, но и облегчит решение, так как значения 0/1 будут подчиняться определенному порядку для каждой переменной.

Графическое решение числовых выражений по координатной прямой

Ряд заданий в алгебре логики основывается в использовании в качестве высказывания числового выражения. Например,

(X > 2) / ¬(X > 5).

Хорошо видно, что выражение берется в скобки для однозначного восприятия. Прежде чем наносить значения на рисунок, следует избавиться от отрицания. В этом случае происходит замена знаков отношения на противоположные по схеме: ↔ ≤, = ↔ ≠.

В нашем примере мы получим

(X > 2) / (X ≤ 5).

Нанесем два значения на координатную прямую и, учитывая логическое И, у нас должны совпасть оба условия. То есть на прямой это будет пересечение, обозначенное красным.

Возможные целочисленные ответы — 3, 4, 5.

Построение логического выражения по таблице истинности

Задача является противоположной стандартной.

При ее решении нужно построить дизъюнкцию для всех строк, равных 1, то есть составить выражение в дизъюнктивной нормальной форме (ДНФ).

Решение текстовых задач

На предыдущих этапах, в частности, изучались графический и табличный способы, которые невозможно, либо чрезмерно трудоемко использовать для сложных заданий. Также, решение задач путем рассуждений зачастую неэффективно.

Многие учащиеся очень расстраиваются, что, используя ранее эти способы, они тратили много времени на то, чтобы выработать стратегию, правильно понимать задание и т.п. А теперь их удается решить буквально за несколько секунд. Эта позиция неверна. Большинство подобных задач в реальной жизни не содержит достаточных сведений для решения средствами алгебры логики. Умение анализировать данные и находить «пробелы» в исходных данных — намного важнее.

При решении логической задачи средствами алгебры логики, необходимо выделить из текста логические условия и записать их в виде выражения.

Каждое высказывание оформляется в виде логической переменной. Чаще всего удобно вводить переменные, обозначенные русскими буквами и связанные с объектами, описанными в задаче: Иван — И, красный — К (или Кр, если переменная К уже введена для Коли) и т.п.

• И, ИЛИ, НЕ.
• «из. следует»; «. влечет»; ЕСЛИ. ТО (импликация)
• «тогда и только тогда», «необходимо и достаточно», «. равносильно. » (эквивалентность).

В большинстве случаев потребуется упрощение выражения с использованием законов алгебры логики.

В некоторых случаях удобно составить систему высказываний (аналогично системе уравнений) и, затем, решать уже её.

Логическое значение категорически рекомендуется записывать как 0 (ложь) или 1 (истина). Это поможет дифференцировать записи, а не спотыкаться о глупейшие варианты Л/И.

Трое друзей поспорили о результатах предстоящих скачек. Иван: Ласточка не придет первой, первой будет Стрела. Сергей: Победит Ласточка, а Тормозу ни за что не быть первым. Петр: Стреле не видать первого места, а Тормоз готовился очень тщательно.

По итогам скачек оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего оказались ошибочными. Кто выиграл этап гонки?

Введем обозначения для логических высказываний:
Л — победит Ласточка; С — победит Стрела; Т — победит Тормоз.
Запишем высказывания (высказывание Петра «Тормоз готовился очень тщательно» не содержит информации о месте и не может быть учтено):

1) ¬Л / С, 2) Л / ¬Т, 3) ¬С.

Учитывая истинность предположений двух друзей и ложность третьего, запишем истинное высказывание, основанное на том, что неправ либо первый, либо второй, либо третий:

Затем упростим его за счет двойного отрицания, правила Моргана и убрав ненужные для первого члена скобки:

[¬Л / С / Л / ¬Т / С] / [(Л / ¬С) / (¬Л / Т) / ¬С] / [(Л / ¬С) / (Л / ¬Т) / ¬С] = 1

Выражение по-прежнему немаленькое. Далее, по закону поглощения можно сократить показанное красным

[ ¬Л / С / Л / ¬Т / С] / [ (Л / ¬С) / (¬Л / Т) / ¬С ] / [ (Л / ¬С) / (Л / ¬Т) / ¬С ] = 1

[(¬Л / Т) / ¬С] / [(Л / ¬Т) / ¬С] = 1

В оставшейся части сократим противоположные слагаемые (по закону исключения третьего)

Конечно, можно сразу сказать, что в произведении все три множителя должны быть равны единице, то есть: Л = 1, Т = 0, С = 0. Ответ: победителем скачек стала Ласточка.

Но можно сделать то же, построив таблицу истинности:

Дополнительная литература

1. Википедия.
2. Логические основы компьютеров.
3. Учебник по алгебре логики.
4. Лемешев С.В. Решение текстовых задач, 2009.

Вопросы и задачи

1. Упростите выражение: (X / Y) → ¬Z.
2. Найдите решения выражения: ((X → Y) / Z) ↔ X.
3. Определите истинность выражения: (Z / X) → (Y / X).
4. Определите истинность выражения: ((C / B)→B) / (A / B))→B.
5. Упростите выражение: A / B / (¬A / B) / C / D.
6. Упростите выражение: (A / B) / (A / B / C).
7. Решить в Excel выражение (без его преобразований): F = ¬X / ¬Y / Z / X / Y.
8. Для какого из названий животных ложно высказывание: ((Заканчивается на согласную букву) / (В слове 7 букв) → ¬(Третья буква согласная))?
   1) Верблюд 2) Страус 3) Кенгуру 4) Леопард
9. Какое из приведенных имен удовлетворяет логическому условию
   ((первая буква гласная → вторая буква гласная) / последняя буква гласная)?
   1) ИРИНА 2) МАКСИМ 3) АРТЕМ 4) МАРИЯ
10. Упростите выражение: A / B / A / B / (C / D).

Источник: it-mda.ru

Укажите ложное высказывание имя программы может совпадать

Главное меню

Соглашение

Регистрация

Английский язык

Астрономия

Белорусский язык

Информатика

Итальянский язык

Краеведение

Литература

Математика

Немецкий язык

Обществознание

Окружающий мир

Русский язык

Технология

Физкультура

Для учителей

Дошкольникам

VIP — доступ

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Получение сертификата
о прохождении теста

Источник: testedu.ru

ОГЭ по информатике — Задание 3 (Логическое выражение)

Привет! Продолжаем разбирать ОГЭ по информатике 2023. Сегодня посмотрим 3 задание.

Третье задание из ОГЭ по информатике проверяет умение работать с логическим выражением.

В логическом выражении могут использоваться союз И и союз ИЛИ.

Пусть 0 — это ложь, 1 — Истина. Тогда напишем таблицу истинности для союза И и для союза ИЛИ.

Таблица истинности для союза И

Союз И похож на умножение в математике. Если в логическом выражении присутствует 0 (ложь), то в итоге тоже получается 0 (ложь). Лишь две единицы дают тоже единицу.

Таблица истинности для союза ИЛИ

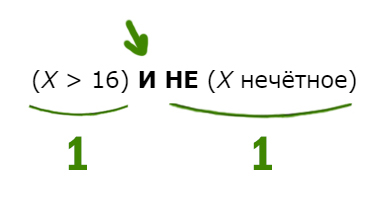
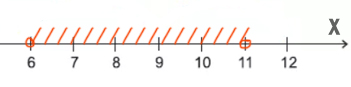
Эта операция похоже на суммирование в математике. Лишь 1 или 1 даёт не 2, как в математике, а 1.

Перейдём к решению примерных задач из ОГЭ по информатике 2023.

Напишите наименьшее число X, для которого истинно высказывание:

(X > 16) И НЕ (X нечётное)
Решение:

Нужно, чтобы высказывание было истинным. Посмотрим, когда единица (истина) получается для союза И. Такое происходит только когда слева и справа стоят 1 (единицы).

Получается наш X должен быть больше 16, и число должно быть не нечётное, т.е. чётное! Наименьшее чётное число большее 16 будет 18.

Напишите наибольшее целое число x, для которого истинно высказывание:

Опять высказывание должно быть истинным.

С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X > 6). Причём само число 6 не входит в этот диапазон.

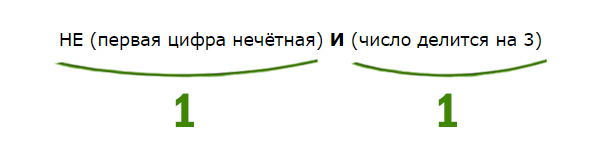
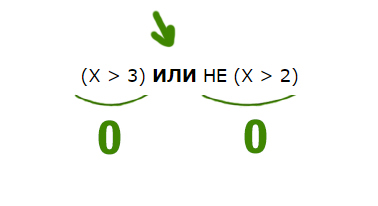
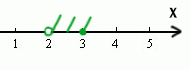
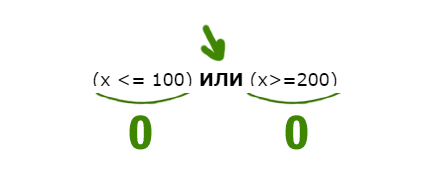
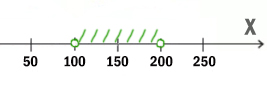
С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X

Наибольшее целое число будет 10.

Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:

НЕ (первая цифра нечётная) И (число делится на 3)
Решение:

Высказывание должно быть истинным.

Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.

Для какого целого числа X ЛОЖНО высказывание:

(X > 3) ИЛИ НЕ (X > 2)
Решение:

В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.

Утверждение, что X > 3 должно быть ложно, значит, если его перевернуть, получится X 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X > 2.

Получается, что только одно целое число входит в допустимый диапазон. Это тройка.

Задача (Частица НЕ над всем выражением)

Напишите наименьшее натуральное число x, для которого истинно высказывание:

Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно.

Ложь у союза ИЛИ получается в одном случае.

Первое выражение выдаёт ноль, когда x>200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x>100. Объединив эти два условия получаем:

Наименьшее число получается 201.

Напишите наименьшее натуральное число x, для которого истинно высказывание:

В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого.

Когда союз И выдаёт единицу ?

Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.

Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X>100, с другой X

Учтём правое от союза И выражение. Наименьшее чётное число получается 102.

Источник: code-enjoy.ru