Рассмотрим блок-схему разветвляющегося алгоритма, или алгоритма ветвящейся структуры. Если после ввода данных оказывается, что условие истинно, то вычислительный процесс идёт по ветви «Да», и выполняется Действие 1. Если же оказывается, что условие ложно, то вычислительный процесс идёт по ветви «Нет», и выполняется Действие 2.
Рисунок 4.1. Блок-схема алгоритма ветвящейся структуры
Алгоритму ветвящейся структуры в языке Pascal соответствуют условный оператор и оператор множественного выбора.
Условный оператор. Операции сравнения. Логические переменные, операции и выражения. Составной оператор.
Теперь мы знаем, что для реализации алгоритма ветвящейся структуры необходимо задать некоторое условие. Условие может быть простым и сложным. Прежде чем рассматривать эти понятия, необходимо дать ряд определений и пояснений.
В математической логике есть понятие высказывания – такого утверждения, о котором можно с уверенностью сказать, истинное оно или ложное. Классическим примером высказывания (принимающего, кстати, истинное значение) является утверждение: «Волга впадает в Каспийское море». Естественно, что запись a> b становится высказыванием, как только будут определены значения переменных a и b.
Ботаем блок-схему | Информатика ОГЭ 2022 | Умскул
Простое условие задаётся посредством простого логического выражения.
Сложное логическое выражение состоит из двух и более простых логических выражений, связанных логическими операциями. Именно сложное логическое выражение используются для записи сложных логических условий.
В математической логике, и, соответственно, в языке Pascal, определены следующие логические операции:
AND – логическое » И» (операция конъюнкции);
OR – логическое » ИЛИ» (операция дизъюнкции);
NOT – логическое » НЕ» (операция отрицания).
Логические выражения используются для организации альтернативного выбора (то есть выбора не более чем из двух возможных вариантов) при разветвлении вычислительного процесса.
Для истинности этого выражения должны быть истинными обе составные его части. Тот же факт, что Х не принадлежит интервалу [a, b], на языке Pascal записывается так:
Истинность логического выражения, содержащего логическое » И», достигается при одновременной истинности обеих составляющих его частей.
Истинность логического выражения, содержащего логическое » ИЛИ» достигается при истинности хотя бы одной (любой) из составляющих его частей.
Теперь необходимо рассмотреть ещё одно понятие: составной оператор. По определению, составной оператор – это последовательность двух или более операторов языка Pascal, заключённых между ключевыми словами begin и end, называемых также операторными скобками. Необходимость в введении составного оператора возникла потому, что синтаксис большинства операторов языка Pascal предполагает, что внутри этих операторов может работать только один оператор. Если же алгоритм предполагает использование более одного оператора, то используется составной оператор, который имеет вид:
Алгоритм. Трассировка. Тестирование. Блок-схема|| информатика 8 класс
Begin
end;
После последнего оператора N точка с запятой («; » ) может не ставиться, так как следом идет ключевое слово end.
Теперь мы можем рассмотреть синтаксис и работу условного оператора.
Условный оператор есть во всех языках программирования. Условный оператор позволяет проверить некоторое условие, и в зависимости от результатов проверки выйти на одну из двух ветвей программы. Другими словами, с помощью этого оператора осуществляется альтернативный выбор ветви программы, по которой пойдет далее вычислительный процесс.
Синтаксис условного оператора в языке Pascal:
Операторы 1 и 2 могут быть простыми или составными. Условный оператор работает следующим образом. Сначала вычисляется значение логического выражения. Если результат есть ИСТИНА, то выполняется оператор 1, а оператор 2 пропускается. Если результат есть ЛОЖЬ, то выполняется оператор 2, а оператор 1 пропускается, и компьютер передаёт управление следующему по порядку оператору программы.
Существует укороченная форма условного оператора, в которой часть оператора ELSE опущена. В этом случае оператор действует следующим образом: если значение логического выражения ИСТИНА, выполняется оператор 1, если ЛОЖЬ, то оператор 1 не выполняется, и компьютер передаёт управление следующему по порядку оператору программы.
Источник: lektsia.com
Алгоритмы разветвленной структуры
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур — блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала-конца алгоритма (рис. 1.1). Надпись на блоке: «начало» («конец»).
Блок ввода-вывода данных (рис. 1.2). Надпись на блоке: слово «ввод» («вывод» или «печать») и список вводимых (выводимых) переменных.
 |
|
| Рис. 1.1. Блок начала-конца алгоритма | Рис. 1.2. Блок ввода-вывода данных |
Блок решения или арифметический (рис. 1.3). Надпись на блоке: операция или группа операций.
Условный блок (рис. 1.4). Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви «+», если условие не выполняется, то выполняется этап по ветви «–».
Линейный алгоритм — это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.5).
| Рис. 1.5 Размещение блоков в линейном алгоритме |
Рассмотрим несколько примеров линейных алгоритмов .
ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.
Пусть a, b, c — длины сторон треугольника. Необходимо найти S — площадь треугольника, P — периметр.
Для нахождения площади можно воспользоваться формулой Герона:
, где r — полупериметр
Входные данные: a, b, c.
Выходные данные: S, P.
Блок-схема алгоритма представлена на рис. 1.6.
| Рис. 1.6. Алгоритм примера 1.1 |
Рассмотрим несколько примеров построения алгоритмов разветвленной структуры.
Пример. Есть детский сад, в котором много детей. Тренер из балетной школы хочет набрать детей в балетную школу. Подойдут только дети не старше трех лет.
Пример. Исследование медицинских данных детей от 7 до 10 лет. (самотоятельно)
Пример. Вычислить y=(a+b)/c, c=a-b
Пример. Вычислить y=(2x+3)/(z-1), z=4-x. (самостоятельно)
ПРИМЕР 1.2. Известны коэффициенты a, b, и с квадратного уравнения. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Выходные данные: x1, x2.
d – дискрименант, вычисляется пл формуле.
Все известные в школе формулы и все вычислительные процедуры высшей математики (интегралы, sin и т.д.), запрограммировано в компьютере.
| Рис. 1.9. Алгоритм решения квадратного уравнения |
ПРИМЕР 1.3. Найти наибольшее из трех чисел.
Входные данные: a, b, c.
Выходные данные: m.
| Рис. 1.10. Алгоритм примера 1.3 |
Пояснения к блок-схеме: вводится дополнительная переменная m, в которой хранится текущее значение наибольшего (максимального) числа. Далее каждое следующее число сравнивается с переменной m и если значение сравниваемого числа оказывается больше, то оно запоминается в переменную m.
ПРИМЕР 1.4. Модель платья окрашена в три базовых цвета: красный, синий, зеленый. Подсчитать частоту встречаемости каждого цвета в модели.
Каждый цвет закодирован: красный – 1, синий – 2, зеленый – 3.
Входные данные: cvet
Выходные данные kol_red, kol_blue, kol_green
Рис. 1.11. Алгоритм примера 1.4.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
Алгоритмические конструкции ветвление и выбор Блок-схемы разветвляющихся алгоритмов

Разветвляющиеся алгоритмы • Вычислительный процесс называется разветвляющимся, если направление его продолжения на некотором этапе в зависимости от исходных данных или результатов промежуточных вычислений осуществляется по одному из возможных вариантов • Варианты вычислений называются ветвями • Разветвляющиеся алгоритмы реализуются через алгоритмические структуры «ветвление» и «выбор»
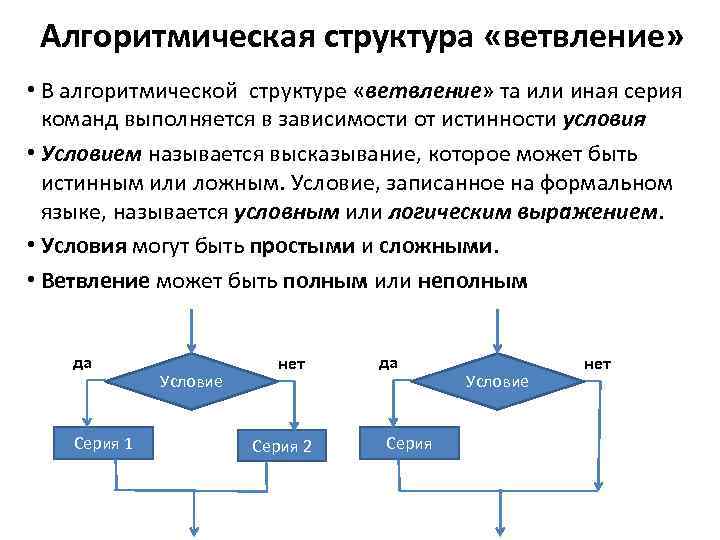
Алгоритмическая структура «ветвление» • В алгоритмической структуре «ветвление» та или иная серия команд выполняется в зависимости от истинности условия • Условием называется высказывание, которое может быть истинным или ложным. Условие, записанное на формальном языке, называется условным или логическим выражением. • Условия могут быть простыми и сложными. • Ветвление может быть полным или неполным да Серия 1 Условие нет Серия 2 да Серия Условие нет
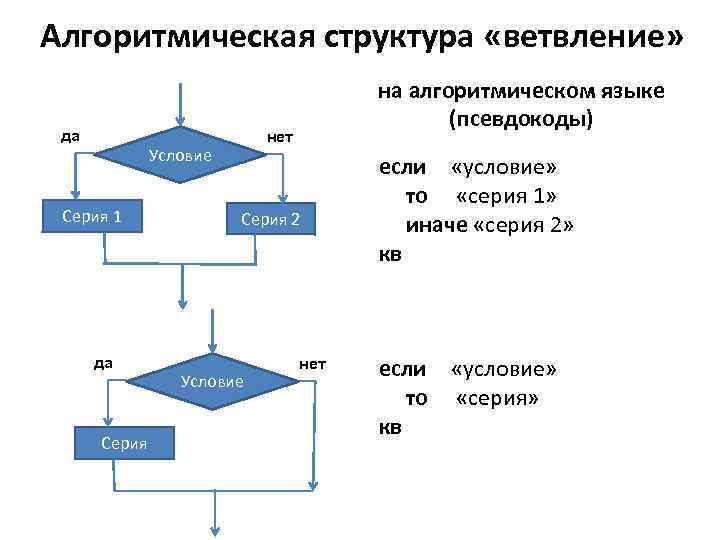
Алгоритмическая структура «ветвление» да нет Условие Серия 1 да Серия на алгоритмическом языке (псевдокоды) Серия 2 Условие нет если «условие» то «серия 1» иначе «серия 2» кв если «условие» то «серия» кв
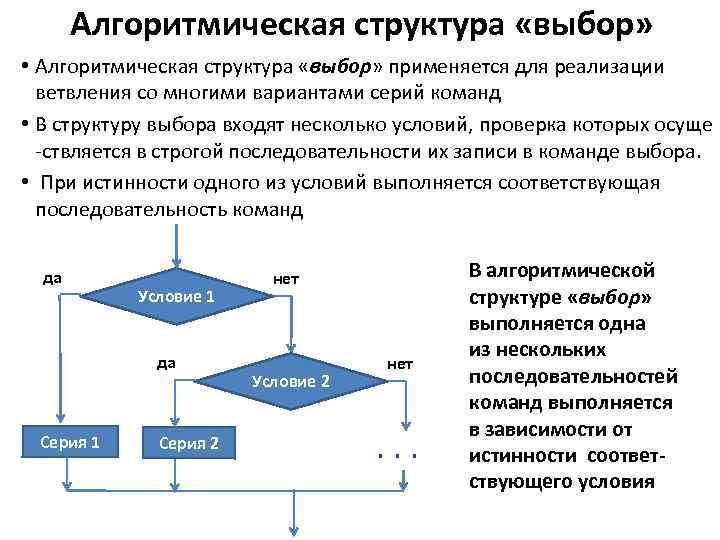
Алгоритмическая структура «выбор» • Алгоритмическая структура «выбор» применяется для реализации ветвления со многими вариантами серий команд • В структуру выбора входят несколько условий, проверка которых осуще -ствляется в строгой последовательности их записи в команде выбора. • При истинности одного из условий выполняется соответствующая последовательность команд да Условие 1 да Серия 1 Серия 2 нет Условие 2 нет . . . 2 В алгоритмической структуре «выбор» выполняется одна из нескольких последовательностей команд выполняется в зависимости от истинности соответствующего условия

Виды задач, решаемых с помощью ветвления • Выбор (минимума или максимума) – из 2 величин – из n величин • Упорядочение (по возрастанию или по убыванию) – 2 величин – n величин
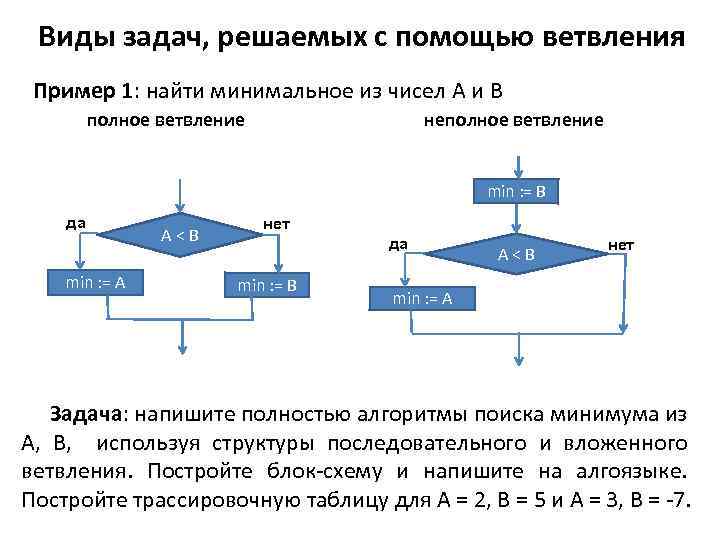
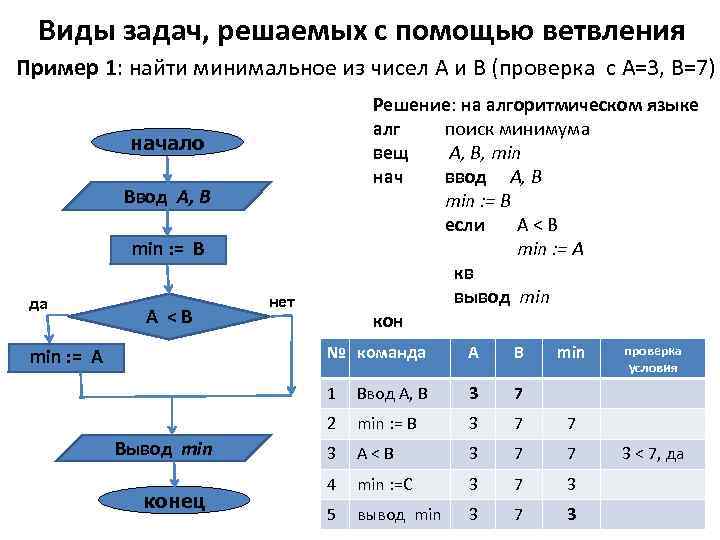
Виды задач, решаемых с помощью ветвления Пример 1: найти минимальное из чисел А и В (проверка с A=3, B=7) Решение: на алгоритмическом языке алг поиск минимума вещ А, В, min нач ввод А, В min : = B если A
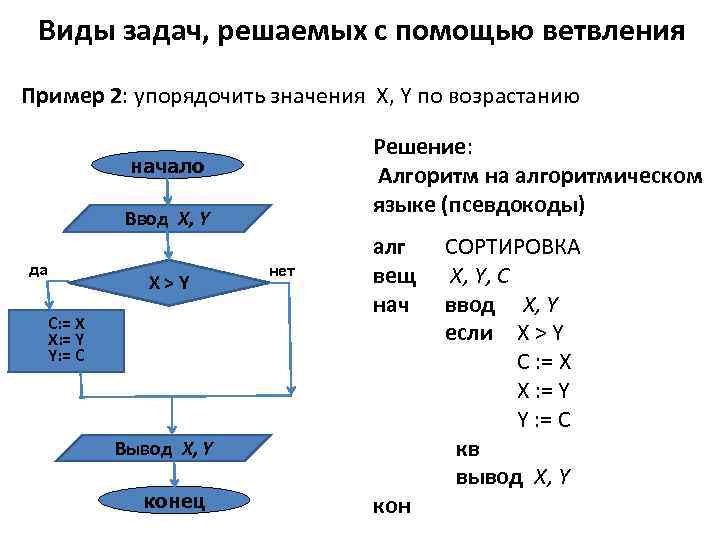
Виды задач, решаемых с помощью ветвления Пример 2: упорядочить значения X, Y по возрастанию Решение: Алгоритм на алгоритмическом языке (псевдокоды) начало Ввод X, Y да X>Y C: = X X: = Y Y: = C нет алг вещ нач Вывод X, Y конец кон СОРТИРОВКА X, Y, C ввод X, Y если X > Y C : = X X : = Y Y : = С кв вывод X, Y
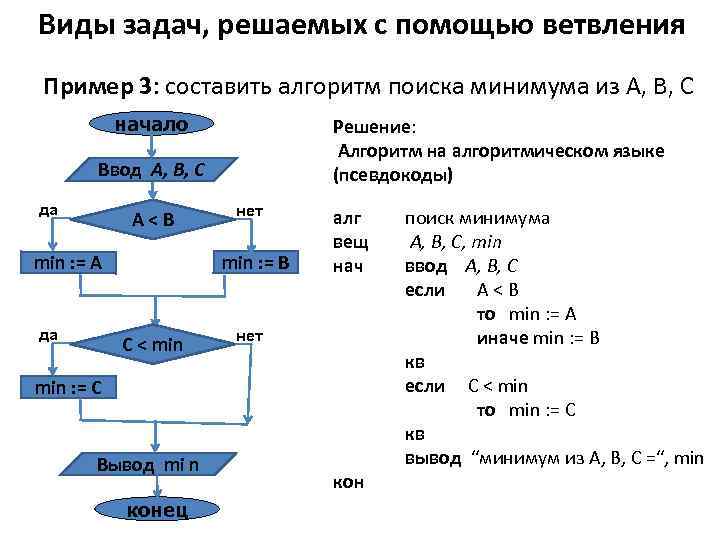
Виды задач, решаемых с помощью ветвления Пример 3: составить алгоритм поиска минимума из А, В, С начало Решение: Алгоритм на алгоритмическом языке (псевдокоды) Ввод А, В, С да А
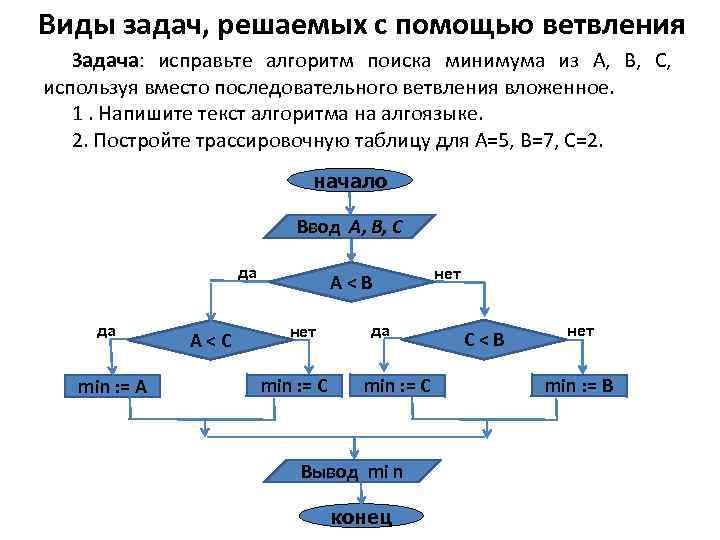
Виды задач, решаемых с помощью ветвления Задача: исправьте алгоритм поиска минимума из А, В, С, используя вместо последовательного ветвления вложенное. 1. Напишите текст алгоритма на алгоязыке. 2. Постройте трассировочную таблицу для А=5, В=7, С=2. начало Ввод А, В, С да да min : = A А

Виды задач, решаемых с помощью ветвления Любой алгоритм должен приводить к определенному результату и завершать работу, какими бы ни были исходные и промежуточные данные. Задача 1: исправьте блок-схему алгоритма деления двух дробей, учитывая, что на 0 делить нельзя. Задача 2: постройте блок-схему решения квадратного уравнения ax 2 + bx + c = 0, учитывая случаи возможного ввода исходных a = 0, b = 0, c = 0, и случай d < 0.

Виды задач, решаемых с помощью ветвления Задача 1: составить алгоритм поиска минимума из А, В, С, D Задача 2: постройте блок-схему для проверки существования треугольника с углами α и β, а в случае удачи также проверьте, будет ли он прямоугольным. Задача 3: постройте блок-схему для проверки, какая из точек A(x 1, y 1) или В(x 2, y 2) лежит ближе к началу координат. Задача 4: постройте блок-схему для вычисления значения функции Y = |X|. Задача 5: постройте блок-схему для проверки, попадает ли точка A(x, y) в определенную область на координатной плоскости (например, а) в первый квадрант, б) в окружность определенного радиуса с центром в начале координат)

Домашняя работа на разветвляющиеся алгоритмы Построить блок-схемы разветвляющихся алгоритмов • Задача 1: «Геометрическая задача» — по вариантам (по карточкам). • Задача 2: «Математическая задача» — по вариантам (по карточкам).
Источник: present5.com