Цикломатическая сложность программы это

Измерение — это не что иное, как количественное указание размера / размера / емкости атрибута продукта / процесса. Метрика программного обеспечения определяется как количественная мера атрибута, которым обладает система программного обеспечения в отношении стоимости, качества, размера и графика.

Пример-

Measure — No. of Errors Metrics — No. of Errors found per person

В этом уроке вы узнаете

• Что такое метрика программного обеспечения?
• Что такое цикломатическая сложность?
• Блок-схема обозначений для программы:
• Как рассчитать цикломатическую сложность
• Свойства цикломатической сложности:
• Насколько этот показатель полезен для тестирования программного обеспечения?
• Подробнее о V (G):
• Инструменты для расчета цикломатической сложности:
• Использование цикломатической сложности:

Что такое цикломатическая сложность?

ЦИКЛОМАТИЧЕСКАЯ СЛОЖНОСТЬ — это метрика программного обеспечения, используемая для измерения сложности программы. Это количественная мера независимых путей в исходном коде программы. Независимый путь определяется как путь, имеющий хотя бы одно ребро, которое ранее не проходило ни в одном другом пути. Цикломатическая сложность может быть рассчитана относительно функций, модулей, методов или классов в программе.

Когнитивная и цикломатическая сложность

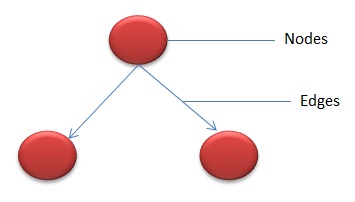
Эта метрика была разработана Томасом Дж. МакКейбом в 1976 году и основана на представлении программы потока управления. Поток управления изображает программу в виде графика, который состоит из узлов и ребер.

На графике узлы представляют задачи обработки, а ребра представляют поток управления между узлами.

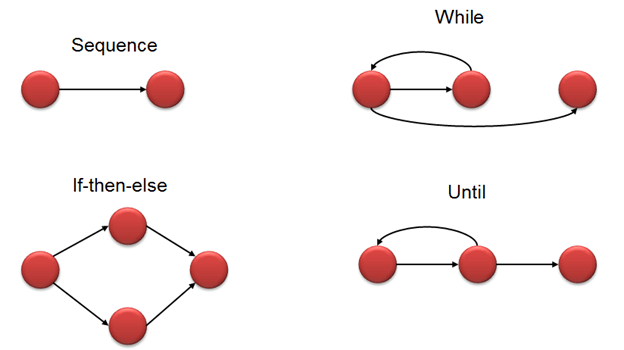
Блок-схема обозначений для программы:

Нотация Flow Graph для программы определяет несколько узлов, соединенных через ребра. Ниже приводятся блок-схемы для операторов типа if-else, while, while и нормальной последовательности потоков.

Как рассчитать цикломатическую сложность

Математическое представление:

Математически это множество независимых путей через диаграмму графа. Код сложности программы можно определить по формуле —

V(G) = E — N + 2

E — количество ребер

N — количество узлов

V (G) = P + 1

Где P = количество узлов предиката (узел, содержащий условие)

i = 0; n=4; //N-Number of nodes present in the graph while (i

График потока для этой программы будет

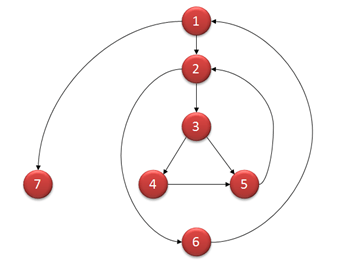
Вычисляя математически,

Как писать простой код

• V (G) = 9 — 7 + 2 = 4
• V (G) = 3 + 1 = 4 (узлами условий являются 1,2 и 3 узла)
• Базисный набор — набор возможных путей выполнения программы
• 1, 7
• 1, 2, 6, 1, 7
• 1, 2, 3, 4, 5, 2, 6, 1, 7
• 1, 2, 3, 5, 2, 6, 1, 7

Свойства цикломатической сложности:

Ниже приведены свойства цикломатической сложности:

1. V (G) — максимальное количество независимых путей в графе
2. V (G)> = 1
3. G будет иметь один путь, если V (G) = 1
4. Минимизировать сложность до 10

Насколько этот показатель полезен для тестирования программного обеспечения?

Тестирование базового пути является одним из методов «белого ящика» и гарантирует выполнение хотя бы одного оператора во время тестирования. Он проверяет каждый линейно независимый путь в программе, что означает , что число тестовых примеров будет эквивалентно цикломатической сложности программы.

Этот показатель полезен из-за свойств цикломатической сложности (M) —

1. M может быть числом тестовых случаев для достижения покрытия ветви (верхняя граница)
2. M может быть числом путей через графы. (Нижняя граница)

Рассмотрим этот пример —

If (Condition 1) Statement 1 Else Statement 2 If (Condition 2) Statement 3 Else Statement 4

Цикломатическая сложность для этой программы составит 8-7 + 2 = 3.

Поскольку сложность рассчитана как 3, для полного охвата пути для приведенного выше примера необходимы три контрольных примера.

Шаги, которым нужно следовать:

Следующие шаги должны быть выполнены для вычисления Cyclomatic сложности и разработки тестовых случаев.

Шаг 1 — Построение графа с узлами и ребрами из кода

Шаг 2 — Идентификация независимых путей

Шаг 3 — Расчет цикломатической сложности

Шаг 4 — Дизайн тестовых случаев

Как только базовый набор сформирован, должны быть записаны тестовые случаи для выполнения всех путей.

Подробнее о V (G):

Цикломатическая сложность может быть рассчитана вручную, если программа небольшая. Автоматизированные инструменты необходимо использовать, если программа очень сложная, так как для этого требуется больше потоковых графов. Основываясь на количестве сложности, команда может сделать вывод о действиях, которые необходимо предпринять для измерения.

Следующая таблица дает обзор по числу сложности и соответствующему значению v (G):

стоимость тестируемости и усилия меньше

Стоимость и усилия — это средний

Стоимость и усилия высоки

Очень высокая стоимость и усилия

Инструменты для расчета цикломатической сложности:

Многие инструменты доступны для определения сложности приложения. Некоторые инструменты расчета сложности используются для конкретных технологий. Сложность может быть найдена по количеству точек принятия решения в программе. Решающими моментами являются if for for for, while, do, catch, case-выражения в исходном коде.

• OCLint — Статический анализатор кода для C и родственных языков
• Reflector Add In — метрики кода для сборок .NET
• GMetrics — поиск метрик в приложениях, связанных с Java

Использование цикломатической сложности:

Цикломатическая Сложность может оказаться очень полезной в

• Помогает разработчикам и тестировщикам определять независимые пути выполнения
• Разработчики могут заверить, что все пути были протестированы хотя бы раз
• Помогает нам больше сосредоточиться на открытых путях
• Улучшение покрытия кода в программной инженерии
• Оценить риск, связанный с приложением или программой
• Использование этих метрик в начале цикла снижает риск программы

Вывод:

Cyclomatic Complexity — это программный показатель, полезный для структурированного тестирования или тестирования White Box . Он в основном используется для оценки сложности программы. Если точек решения больше, то сложность программы больше. Если программа имеет большое число сложности, то вероятность ошибки высока с увеличением времени на обслуживание и устранение неисправностей.

Источник: coderlessons.com

Цикломатическая сложность алгоритма и цикломатическое число графа кратко

Привет, Вы узнаете про цикломатическая сложность, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое цикломатическая сложность, цикломатическое число , настоятельно рекомендую прочитать все из категории Качество и тестирование программного обеспечения. Quality Assurance..

цикломатическая сложность программы (англ. cyclomatic complexity of a program) — структурная (или топологическая) мера сложности компьютерной программы. Мера была разработана Томасом Дж. Маккейбом в 1976 году. При вычислении цикломатической сложности используется граф потока управления программы.

Узлы графа соответствуют неделимым группам команд программы, они соединены ориентированными ребрами, если группа команд, соответствующая второму узлу, может быть выполнена непосредственно после группы команд первого узла. Цикломатическая сложность может быть также вычислена для отдельных функций, модулей, методов или классов в пределах программы. Маккейб применял вычисление цикломатической сложности при тестировании. Предложенный им метод заключался в тестировании каждого линейно независимого маршрута через программу, в этом случае число необходимых тестов равно цикломатической сложности программы.

Описание

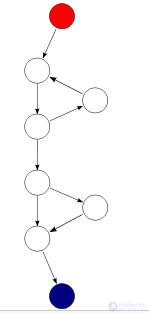
Граф управления потоком простой программы. Программа начинает выполняться с красного узла, затем идут циклы (после красного узла идут две группы по три узла). Выход из цикла осуществляется через условный оператор (нижняя группа узлов) и конечный выход из программы в синем узле. Для этого графа E = 9, N = 8 и P = 1, цикломатическая сложность программы равна 9 − 8 + 2 × 1 = 3 (рассчитано по первому варианту)

Цикломатическая сложность части программного кода — количество линейно независимых маршрутов через программный код. Например, если исходный код не содержит никаких точек ветвления или циклов, то сложность равна единице, поскольку есть только единственный маршрут через код. Если код имеет единственный оператор IF , содержащий простое условие, то существует два пути через код: один если условие оператора IF имеет значение TRUE и один — если FALSE . Математически цикломатическая сложность структурированной программы определяется с помощью ориентированного графа, узлами которого являются блоки программы, соединенные ребрами, если управление может переходить с одного блока на другой. Тогда сложность определяется как: : M = E − N + 2P, где: M = цикломатическая сложность, E = количество ребер в графе, N = количество узлов в графе, P = количество компонент связности.

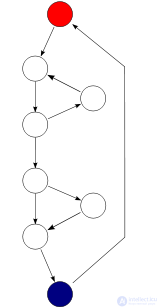
Сильносвязный граф управления потоком той же функции . Об этом говорит сайт https://intellect.icu . Для этого графа E = 10, N = 8 и P = 1, следовательно, цикломатическая сложность программы, рассчитанная по второму варианту, также равна 10 − 8 + 1 =3

В другой формулировке используется граф, в котором каждая точка выхода соединена с точкой входа. В этом случае граф является сильносвязным, и цикломатическая сложность программы равна цикломатическому числу этого графа (также известному как первое число Бетти), которое определяется как M = E − N + P.

Это определение может рассматриваться как вычисление числа линейно независимых циклов, которые существуют в графе, то есть тех циклов, которые не содержат в себе других циклов. Так как каждая точка выхода соединена с точкой входа, то существует по крайней мере один цикл для каждой точки выхода. Для простой программы, или подпрограммы, или метода P всегда равно 1. Однако цикломатическая сложность может применяться к нескольким таким программам или подпрограммам (например, ко всем методам в классе), в таком случае P равно числу подпрограмм, о которых идет речь, так как каждая подпрограмма может быть представлена как независимая часть графа. Может быть показано, что цикломатическая сложность любой структурированной программы с только одной точкой входа и одной точкой выхода эквивалентна числу точек ветвления (то есть, операторов if или условных циклов), содержащихся в этой программе, плюс один. Цикломатическая сложность может быть распространена на программу с многочисленными точками выхода; в этом случае она равна π − s + 2, где: π — число точек ветвления в программе, s — число точек выхода.

Формальное определение

Формально, цикломатическая сложность может быть определена как относительное число Бетти: то есть «первая гомология графа G относительно терминальных узлов t. Это другой способ сказать «число линейно независимых маршрутов через граф от входа к выходу». Кроме того, цикломатическую сложность можно вычислить через абсолютное число Бетти (с помощью абсолютной гомологии, а не относительной), объединив все терминальные узлы данного компонента (что эквивалентно соединению точек выхода с точкой входа), в этом случае для нового, расширенного, графа

цикломатическое число графа

Цикломатическим числом графа называется число, равное увеличенной на единицу разности между числом ребер и числом вершин графа: 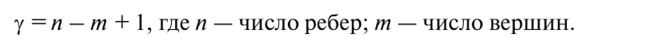Цикломатическое число графа показывает, сколько ребер надо удалить из графа, чтобы в нем не осталось ни одного цикла. Задача 1. Дан граф, у которого т = 6, п = 9 (рис.

8.18, а). Определить, сколько ребер на графе нужно удалить, чтобы в нем не осталось ни одого цикла. 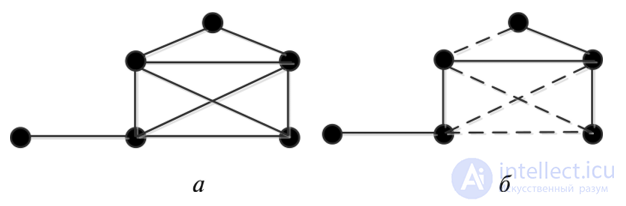Рис. 8.18.

Исходный граф (о) и остовный подграф (б) (——-) удаленные ребра Для заданного графа цикломатическое число у = 9 — 6 + 1 = 4. Это означает, что если на графе удалить 4 ребра, то в нем не останется ни одного цикла. Тогда остовный подграф будет иметь вид, показанный на рис. 8.18, б. Задача 2. Какое минимальное число дверей нужно предусмотреть в замке (рис.

8.19), чтобы попасть во все комнаты (дверь — одно ребро). 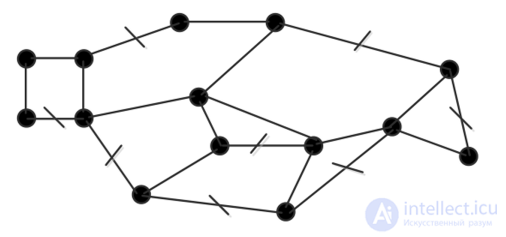Рис. 8.19. Схема замка (вид сверху) Решение. Число вершин т = 14, число ребер п = 21.

Цикломатическое число у = 21 — 14+1 = 8. Следовательно, в замке нужно предусмотреть 8 дверей. Наряду с цикломатическим числом в теории графов вводится понятие коцикломатического числа. Пусть в графе т — число ребер, п — число вершин, р — число компонент связности. Величина г = п—р называется коцикломатическим числом (число ребер в остовах всехр связных компонент графа).

Применение

Ограничение сложности при разработке

Одно из первоначально предложенных Маккейбом применений состоит в том, что необходимо ограничивать сложность программ во время их разработки. Он рекомендует, чтобы программистов обязывали вычислять сложность разрабатываемых ими модулей и разделять модули на более мелкие всякий раз, когда цикломатическая сложность этих модулей превысит десять. Эта практика была включена НИСТ-ом в методику структурного тестирования с замечанием, что со времени исходной публикации Маккейба выбор значения 10 получил весомые подтверждения, однако в некоторых случаях может быть целесообразно ослабить ограничение и разрешить модули со сложностью до 15. В данной методике признается, что иногда могут существовать причины для выхода за рамки согласованного лимита. Это сформулировано как рекомендация: «Для каждого модуля следует либо ограничивать цикломатическую сложность до согласованных пределов, либо предоставить письменное объяснение того, почему лимит был превышен».

Применение при тестировании программного обеспечения

• M — оценка сверху для количества тестов, обеспечивающих покрытие условий (точек ветвления);
• M — оценка снизу для количества маршрутов через граф потока управления и, таким образом, количества тестов для полного покрытия путей.

В составе других метрик

Цикломатическая сложность используется в качестве одного из параметров в индексе удобства сопровождения (англ. maintainability index) .

Вау!! Ты еще не читал? Это зря!

• Качество программного обеспечения
• Аварии по причине сбоя ЭВМ‎
• Антипаттерны
• Формальные методы
• Качество программного обеспечения
• Вязкость ( программирование )
• Долгосрочная поддержка программного обеспечения
• Когнитивные измерения
• Кризис программного обеспечения
• Обеспечение качества программного обеспечения
• Обходной прием
• Статистическая модель Миллса
• Тупиковая запись
• Цикломатическая сложность
• Эффект второй системы
• Capability Maturity Model
• FURPS
• технический долг

В общем, мой друг ты одолел чтение этой статьи об цикломатическая сложность. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.

Надеюсь, что теперь ты понял что такое цикломатическая сложность, цикломатическое число и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Качество и тестирование программного обеспечения. Quality Assurance.

Источник: intellect.icu

Цикломатическая сложность в Swift

Сегодня мы поговорим о цикломатической сложности в Swift.

Вы когда-нибудь чувствовали, что ваш код выходит из-под контроля? Вам трудно понять или поддерживать определенную функцию или модуль в вашем приложении? Если да, то вы можете столкнуться с проблемой цикломатической сложности, и это более распространенное явление, чем вы думаете.

Цикломатическая сложность — это модный термин, обозначающий количество точек принятия решений в коде. На самом деле это очень просто. По сути, чем больше у вас точек принятия решений — например, операторов if, switch, циклов и так далее, — тем сложнее становится ваш код. А чем сложнее код, тем труднее его понимать, тестировать и поддерживать.

Разработчику Swift важно знать о цикломатической сложности и о том, как она влияет на качество и сопровождаемость вашего кода. Высокий уровень цикломатической сложности может затруднить отладку и оптимизацию вашего приложения и привести к повышенному риску ошибок и недочетов.

Но не волнуйтесь, есть стратегии, которые вы можете использовать для снижения цикломатической сложности и улучшения качества вашего Swift-кода. Разбивая сложные функции на более мелкие модульные части и используя операторы потока управления, такие как guard и if let, для упрощения точек принятия решений, вы можете сделать свой код более эффективным и простым в сопровождении.

В этой статье мы подробно рассмотрим, что такое цикломатическая сложность, почему она важна для разработчиков и стратегии ее уменьшения в вашем коде. К концу этой статьи вы будете вооружены знаниями и инструментами, необходимыми для написания более чистого и удобного для сопровождения кода на Swift, что сделает вашу жизнь как разработчика проще и приятнее.

Что такое цикломатическая сложность в Swift?

Цикломатическая сложность — это количественный показатель числа линейно независимых путей в исходном коде программы. Он измеряет количество точек принятия решений или ответвлений в программе и сложность логики, используемой для навигации по этим ответвлениям.

Чем выше цикломатическая сложность, тем сложнее поток управления в приложении. Когда мы разрабатываем программное обеспечение, мы всегда стремимся к наименьшей сложности, чтобы обеспечить хорошую сопровождаемость кода.

Почему цикломатическая сложность в Swift имеет значение?

Высокая цикломатическая сложность может сделать код более трудным для чтения, понимания и сопровождения. Это может привести к тому, что код будет сложнее тестировать, отлаживать и модифицировать. Высокая сложность может увеличить вероятность ошибок в коде, исправление которых может быть дорогостоящим.

Снижая цикломатическую сложность программы, разработчики могут облегчить понимание, сопровождение и тестирование кода, что в конечном итоге приведет к уменьшению количества ошибок и повышению эффективности разработки.

Измерение цикломатической сложности в Swift

Цикломатическую сложность можно измерить с помощью формулы, основанной на количестве точек принятия решений и количестве линейно независимых путей в коде. В Swift для измерения цикломатической сложности разработчики могут использовать такие инструменты, как встроенный статический анализатор Xcode или инструменты сторонних разработчиков, например SwiftLint.

Статический анализатор Xcode обеспечивает визуализацию потока управления программы, выделяя точки принятия решений и циклы. Он также предоставляет значение цикломатической сложности для каждого метода или функции.

SwiftLint — популярный сторонний инструмент, который включает в себя правило ограничения цикломатической сложности, которое может быть настроено в соответствии со стандартами разработки в комапнии.

Пример

Посмотрите приведенный ниже код:

func calculateGrade(score: Int) -> String < switch score < // first branch case 90. 100: return «A» case 80..else < if score >100 < // third nested branch return «Invalid score» >else < return «Unknown error» >> > >

Эта функция принимает на вход числовой балл и возвращает буквенную оценку на основе шкалы оценок. Однако она имеет высокую цикломатическую сложность из-за множества точек принятия решений в коде.

В частности, в функции есть два оператора switch и вложенные операторы if внутри дефолтного switch. Эти точки принятия решений увеличивают цикломатическую сложность функции и делают ее более сложной для понимания, тестирования и сопровождения.

Чтобы уменьшить цикломатическую сложность этой функции, вы можете рассмотреть возможность ее рефакторинга, чтобы использовать меньше точек принятия решений или разбить ее на более мелкие, более модульные функции.

Давайте решим эту проблему прямо сейчас!

Уменьшение цикломатической сложности в Swift

Чтобы уменьшить цикломатическую сложность в Swift, разработчики могут использовать несколько приемов. Один из распространенных методов — упрощение потока управления путем использования защитных операторов вместо вложенных операторов if. Это может сделать код более читабельным и сократить количество ветвлений в коде.

Другая техника заключается в рефакторизации сложных методов или функций на более мелкие, более управляемые части. Это позволяет разбить сложный код на более мелкие и понятные фрагменты, которые легче тестировать и поддерживать.

Решение проблемы

Для решения приведенного выше примера нам нужно просто извлечь логику и поместить ее в оператор guard.

Посмотрите на решение ниже:

func calculateGrade(score: Int) -> String < guard score >= 0 score switch score < // one branch case 90. 100: return «A» case 80..>

Это решение интересно тем, что теперь у нас больше нет вложенных ветвей/точек, и наш код действительно легко понимать. А это, друзья мои, и есть цель устранения цикломатической сложности вашего кода.

Заключение

Цикломатическая сложность — это важный аспект качества кода, который может повлиять на читаемость, сопровождаемость и тестируемость программы. Понимая и измеряя цикломатическую сложность в коде, разработчики могут повысить качество и эффективность своей работы.

Я надеюсь, что отныне вы будете дважды думать увеличивая количество вложенных ветвей/if в своем приложении, ваше будущее будет вам благодарно!

Источник: apptractor.ru