Теория чисел – одна из древнейших математических теорий. Арифметические исследования послужили базой для создания ряда разделов математики и, в то же время, теория чисел использует аналитические, алгебраические, геометрические и многие другие методы для решения теоретико-числовых проблем.
Делимость – фундаментальное понятие алгебры, арифметики и теории чисел, связанное с операцией деления. Вопросами делимости чисел занимались еще математики Древней Греции. В теории чисел ими была проведена большая работа по типологии натуральных чисел. Они делили множество натуральных чисел на классы, выделяя классы совершенных чисел, дружественных чисел, фигурных чисел, простых чисел и др.
В книге Евклида «Начала» содержится доказательство бесконечности множества простых чисел. Древнегреческий ученый Эратосфен нашел способ составления таблиц простых чисел, названный позднее «решето Эратосфена».
Вклад в изучение признаков делимости чисел внес Блез Паскаль. Он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, из которого следуют все частные признаки.
Требования к рабочим программам урочной и внеурочной
Проблемами делимости чисел на уроках математики занимались многие математики и методисты: Ж. Адамар, В.Г. Болтянский, И.М. Виноградов, В.А. Далингер, Д. Пойа, Г.И. Саранцев, К.П. Сикорский, А.А.
Столяр, П.Л. Чебышев и др.
В основном, элементы теории чисел в школьном курсе математики представлены в разделах «Делимость натуральных чисел», «Делимость чисел». Тема «Делимость чисел» включена в программу по математике для 5- 6 классов и почти не рассматривается в 7-11 классах. Хотя в контрольно-измерительных материалах государственной итоговой аттестации задачи по элементам теории чисел присутствуют, что делает необходимым включение таких задач в школьный курс алгебры 7-9 классов, старшей школы и обуславливает актуальность темы исследования.
Объект исследования: элементы теории чисел в школьном курсе математики.
Предмет исследования: организация обучения элементам теории чисел в школьном курсе математики.
Цель исследования – разработать программу элективного курса «Элементы теории чисел» для учащихся 10 класса.
Задачи исследования:
- Обобщить значение тории чисел в школьном курсе математики.
- Рассмотреть основные понятия «Теории чисел», изучаемые в школьном курсе математики».
- Проанализировать учебно-методическую литературу по теме исследования.
- Разработать программу элективного курса «Элементы теории чисел» для учащихся 10 класса.
- Провести педагогический эксперимент и проанализировать его результаты.
Гипотеза: разработка и внедрение элективного курса «Элементы теории чисел» в учебный процесс способствует более успешному изучению математики.
Источник: eee-science.ru
Презентация, доклад ТРЕБОВАНИЯ К ПРОГРАММАМ ЭЛЕКТИВНЫХ КУРСОВ И МЕТОДИКА ИХ РАЗРАБОТКИ в образовательной области «Математика»
Вы можете изучить и скачать доклад-презентацию на тему ТРЕБОВАНИЯ К ПРОГРАММАМ ЭЛЕКТИВНЫХ КУРСОВ И МЕТОДИКА ИХ РАЗРАБОТКИ в образовательной области «Математика». Презентация на заданную тему содержит 49 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Юрьева Е.В. — Рабочая программа учителя как средство реализации требований ФГОС
Презентации » Образование » ТРЕБОВАНИЯ К ПРОГРАММАМ ЭЛЕКТИВНЫХ КУРСОВ И МЕТОДИКА ИХ РАЗРАБОТКИ в образовательной области «Математика»





























Элективные курсы в системе школьного математического образования
Цулина, И. В. Элективные курсы в системе школьного математического образования / И. В. Цулина. — Текст : непосредственный // Молодой ученый. — 2009. — № 11 (11). — С. 326-327. — URL: https://moluch.ru/archive/11/697/ (дата обращения: 12.07.2023).
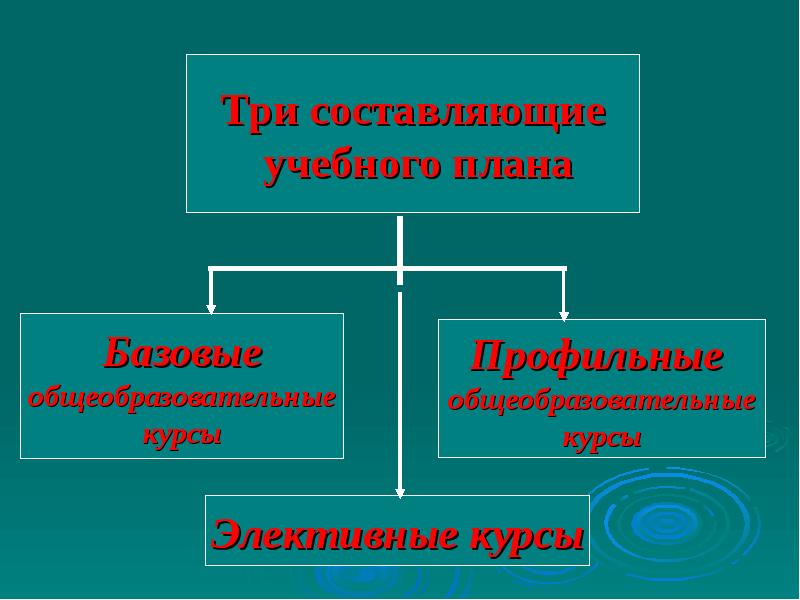
Важным аспектом организации профильного обучения в старшей школе является проектирование и реализация элективных курсов в образовательном процессе. Создание элективных курсов – важнейшая часть обеспечения профильного обучения. Элективные курсы представляют собой обязательные для посещения курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы.
Особенность элективных курсов состоит в том, что учащийся из предложенного набора курсов может выбрать те, которые ему интересны или нужны с точки зрения дальнейшей профессиональной деятельности. Как только курс выбран, он становится нормативным, то есть учащийся обязан его посещать и выполнить по нему соответствующую отчетную работу (сдать зачет, защитить проект и т.д.).
Набор элективных курсов на основе базисного учебного плана определяется самой школой. Элективные курсы должны быть построены на принципах: практической направленности и дифференцированного подхода, а также использования новых педагогических и информационных технологий в обучении.
Приведем существующие типы элективных курсов. По классификации В.А. Орлова среди элективных курсов можно выделить предметные, межпредметные (интегративные), а также курсы, не входящие в базисный учебный план [7].
Предметные элективные курсы по математике можно разделить на две группы. К первой группе относятся элективные курсы повышенного уровня, направленные на углубленное изучение математики и имеющие с ее базовым курсом как тематическое, так и временное согласование. Выбор такого элективного курса позволит изучить математику не на профильном, а на углубленном уровне.
В этом случае все разделы математики углубляются более или менее равномерно. Примером такого элективного курса может стать курс «Обоснования в математике (от Евклида до компьютера)» или «Алгебра плюс: элементарная алгебра с точки зрения высшей математики». Содержание таких курсов рассчитано на учащихся физико-математического или естественнонаучного профилей, а также предъявляет к учителю требования знаний основ высшей алгебры, поскольку уровень сложности предлагаемых для решения задач в курсе очень высокий. Содержание курса может служить хорошей основой для обобщения и систематизации математических знаний учащихся и подготовки к единому государственному экзамену.
Ко второй группе относятся элективные курсы, в которых углубленно изучаются отдельные разделы математики, входящие в обязательную программу. Примерами таких курсов могут быть: «Алгебра и теория пределов» [4], «Красавицы функции и их графики» [15], «Многогранники» [12], «Изображение пространственных фигур» [11], «Избранные вопросы геометрии: обобщения и применения теоремы Пифагора», «Основы комбинаторики», «Замечательные неравенства: способы получения и примеры применения» [3], «Элементы математической статистики», «Элементы теории вероятностей», «Элементы логики» и др. Очевидно, что в элективных курсах данного типа выбранная тема изучается глубже, чем это происходит при выборе учеником элективного курса повышенного уровня.
Курсы, не входящие в базисный план делятся на:
ü Элективные курсы, посвященные истории развития математики и основных ее разделов.Например: «История теории вероятностей» или «Мир, математика, математики (историческая реконструкция элементарной алгебры и математического анализа)», «Математический язык через призму естественного языка или язык математики». Содержание последнего посвящено истории написания цифр, способам изложения доказательств, а также элементам математического языка, вошедших в общую культуру человека.
ü Элективные спецкурсы, в которых углубленно изучаются отдельные разделы основного курса, не входящие в обязательную программу данного предмета. Например, «Табличные методы в логике» [2], «Графы», «Элементы теории множеств», «Элементы теории игр», «Формальная логика» [13], «Логика» [5], «Исследовательская и проектная деятельность школьников» [14], «Математическая культура школьника», «Методы оптимизации. Применение математических методов в экономике» [6] и др.
Межпредметные элективные курсы подразделяются на:
ü Прикладные элективные курсы, цель которых – познакомить учащихся с важнейшими методами применения математических знаний на практике, а также развить интерес у учащихся к современной технике и производству. Приведем возможные примеры таких курсов: «Мировоззренческие аспекты математики» [9], «Геометрическое моделирование окружающего мира» [8], «Курс прикладной математики с изучением основ экономики», «Математика в архитектуре» и др.
ü Элективные курсы, посвященные изучению методов познания природы.Примерами таких курсов могут быть: «Дифференциальные уравнения как математические модели реальных процессов», «Геометрическое моделирование окружающего мира», «Математические модели и методы в естествознании и технике» и др.
ü Элективные курсы, посвященные изучению методов решения математических задач,составлению и решению задач на основе физического, химического, биологического эксперимента.
ü Междисциплинарные элективные курсы,например «Математические основы информатики» [1], который адресован учащимся классов физико-математического профиля, интересующихся информатикой и для старшеклассников информационно-технологического профиля. Содержание курса носит интегративный характер, а его освоение предполагает формирование системы междисциплинарных связей, например, как в элективном курсе «Основы компьютерной алгебры» [10].
Далее обратимся к функциям элективных курсов. Элективные курсы служат «надстройками» профильного курса математики. Именно за их счет такой дополненный профильный курс становится в полной мере углубленным (а школа (или класс), в котором он изучается, превращается в традиционную школу с углубленным изучением математики).
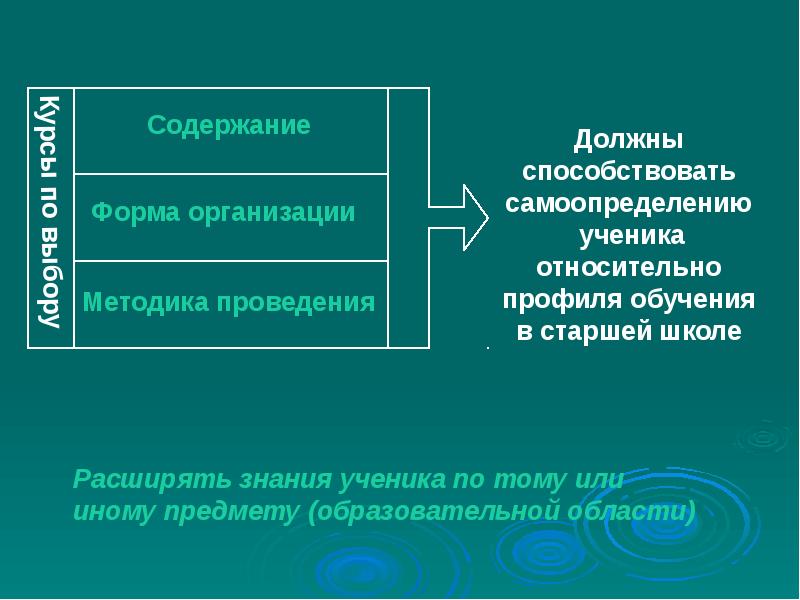
И, наконец, элективный курс важен для внутрипрофильной специализации обучения и для построения индивидуальных образовательных траекторий учащихся. Элективные курсы должны помочь учащемуся в решении двух важнейших задач. Первая из них — создание условий для того, чтобы ученик утвердился в сделанном им выборе направления дальнейшего обучения, связанного с определенным видом профессиональной деятельности, или отказался от него.Вторая задача — помочь старшекласснику, совершившему первоначальный выбор образовательной области для более тщательного изучения, увидеть многообразие видов деятельности, связанных с ней.
По отношению к школьному учителю элективный курс выполняет стимулирующую функцию. Посредством повсеместного введения элективных курсов в учебный план школы в ближайшем будущем учителя будут поставлены перед необходимостью осваивать современные образовательные технологии, потому иного пути для проектирования и проведения элективных курсов нет.
1. Андреева Е.В. «Математические основы информатики: элективный курс», методическое пособие, Бином,2007, 312с.
2. Антонова О.А. «Табличные методы в логике», издательский дом Санкт-Петербургского университета, 2003, 254 с.
3. Гомонов С.А. «Замечательные неравенства: способы получения и примеры применения», Дрофа, 2007, 159 с.
4. Епихин В.Е. «Алгебра и теория пределов: элективный курс», методическое пособие, Бином, 2006, 352 с.
5. Ксенофонтов В. «Логика», изд-во РАГС, 2008, 91 с.
6. Монахов В.М., Беляева Э.С., Краснер Н.Я. «Методы оптимизации. Применение математических методов в экономике», 1978., 176 с.
7. Орлов В.А. Типология элективных курсов и их роль в организации профильного обучения// http://www.college.ru. — [Электронный ресурс].
8. Орлов В.В., Подходова Н.С., Ермак Е.А., Иванова И.А. «Геометрическое моделирование окружающего мира 10-11 классы», хрестоматия, 2007, 176 с.
9. Павлова С.Н. Программа элективного курса для учащихся гуманитарных профилей 10-11-х классов «Мировоззренческие аспекты математики» //Практика административной работы в школе.-2007.-№1.-С.31-33.
10. Поднебесова Г.Б. «Основы компьютерной алгебры», Элективный курс, методическое пособие, изд-во Бином, 2009. – 47 с.
11. Смирнова И.М., Смирнов В.А. «Изображение пространственных фигур», элективный курс, М.Мнемозина,2007, 63 с.
12. Смирнова И.М., Смирнов В.А. «Многогранники»: элективный курс. 10-11 кл., М. Мнемозина, 2007.
13. Сухова Я.Ю. Формальная логика: элективный курс//Профильная школа.-2006.-№3.-С.31-33.
14. Тлиф В.А. Программа элективного курса для профильных классов общеобразовательной школы «Исследовательская и проектная деятельность школьников» // Исследовательская работа школьников//2006.-№3.-С.109-116.
15. Токарчук Н. «Красавицы функции и их графики», серия «Элективный курс», изд-во «Корифей», 2006, 80 с.
Похожие статьи
Профильное обучение и элективные курсы в средней школе
Программа элективного курса «Параметр — это здорово!»
Ценность элективного курса заключается в том, что он позволяет обеспечить индивидуализацию образовательного процесса. Задачи с параметрами по содержанию, сложности и непохожести на все другие можно отнести к задачам нестандартного.
Рабочая программа элективного курса по математике в 7 классе
Элективный курс «Решение математических задач» рассчитан на 35 часов (1 час в неделю) для работы с учащимися 7 классов и предусматривает повторное и параллельное с основным предметом «Математика -7» рассмотрение теоретического материала по математике.
Оптимизационные задачи в школьном курсе математики
Подобный элективный курс будет способствовать как подготовке обучающихся к единому государственному экзамену по математике, так и построению ими собственной образовательной траектории, определению своего дальнейшего жизненного пути.
О разработке элективного курса «Теория принятия решений. »
Ключевые слова: старшие школьники,профильное обучение, межпредметный элективный курс, теория принятия решений, методы оптимизации, математическое моделирование.
Элективный курс ««Некоторые специальные числа натурального.
число, элективный курс, натуральный ряд, четное совершенное число, математик, основная школа, Единый Государственный Экзамен, интеграционная основа, общее образование, самое число.
Методика использования электронного учебника на уроках.
При проведении элективного курса «Живая геометрия», 8 класс используется электронное учебное пособие «Математика, 5–11 кл. Практикум. 1 С: Школа. Геометрия» Многим учащимся «тяжело» запомнить теоремы, правила, формулы и аксиомы.
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Похожие статьи
Профильное обучение и элективные курсы в средней школе
Программа элективного курса «Параметр — это здорово!»
Ценность элективного курса заключается в том, что он позволяет обеспечить индивидуализацию образовательного процесса. Задачи с параметрами по содержанию, сложности и непохожести на все другие можно отнести к задачам нестандартного.
Рабочая программа элективного курса по математике в 7 классе
Элективный курс «Решение математических задач» рассчитан на 35 часов (1 час в неделю) для работы с учащимися 7 классов и предусматривает повторное и параллельное с основным предметом «Математика -7» рассмотрение теоретического материала по математике.
Оптимизационные задачи в школьном курсе математики
Подобный элективный курс будет способствовать как подготовке обучающихся к единому государственному экзамену по математике, так и построению ими собственной образовательной траектории, определению своего дальнейшего жизненного пути.
О разработке элективного курса «Теория принятия решений. »
Ключевые слова: старшие школьники,профильное обучение, межпредметный элективный курс, теория принятия решений, методы оптимизации, математическое моделирование.
Элективный курс ««Некоторые специальные числа натурального.
число, элективный курс, натуральный ряд, четное совершенное число, математик, основная школа, Единый Государственный Экзамен, интеграционная основа, общее образование, самое число.
Методика использования электронного учебника на уроках.
При проведении элективного курса «Живая геометрия», 8 класс используется электронное учебное пособие «Математика, 5–11 кл. Практикум. 1 С: Школа. Геометрия» Многим учащимся «тяжело» запомнить теоремы, правила, формулы и аксиомы.
Источник: moluch.ru
>»>