VladHub18 / Task EGE 23.py
Clone via HTTPS Clone with Git or checkout with SVN using the repository’s web address.
Learn more about clone URLs
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters
| #У исполнителя Калькулятор три команды, которым присвоены номера: |
| #1. прибавь 1 |
| #2. умножь на 2 |
| #3. умножь на 3 |
| #Сколько есть программ, которые число 1 преобразуют в число 18? |
| def numProg ( start , x ): |
| if start == x : # если цель достигнута, то |
| return 1 # завершить функцию, посчитав цепочку (программу) |
| if start > x : # если перелет, то |
| return 0 # завершить функцию, не считая цепочку |
| if start < x : #продолжаем строить дерево |
| return numProg ( start + 1 , x ) + numProg ( start * 2 , x ) + numProg ( start * 3 , x ) |
| print ( numProg ( 1 , 18 ) ) |
| #Исполнитель М17 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: |
| #1. Прибавить 1 |
| #2. Прибавить 2 |
| #3. Умножить на 3 |
| #Сколько существует программ, для которых при исходном числе 2 результатом является число 12 и |
| #при этом траектория вычислений содержит числа 8 и 10? |
| def numProg ( start , x ): |
| if start == x : |
| return 1 |
| if start > x : |
| return 0 |
| if start < x : |
| return numProg ( start + 1 , x ) + numProg ( start + 2 , x ) + numProg ( start * 3 , x ) |
| print ( numProg ( 2 , 8 ) * numProg ( 8 , 10 ) * numProg ( 10 , 12 )) #Если траектория содержит точки, |
| #то можно представить как метод интервалов с пуcтыми точками |
| #Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: |
| #1. Прибавить 1 |
| #2. Умножить на 2 |
| #Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и |
| #при этом траектория вычислений содержит число 14 и не содержит числа 25? |
| def numProg ( start , x ): |
| if start == x : |
| return 1 |
| if start == 25 or start > x : #Если x=25 или перелет, то завершить функцию, не считая цепочку |
| return 0 |
| if start < x : |
| return numProg ( start + 1 , x ) + numProg ( start * 2 , x ) |
| print ( numProg ( 2 , 14 ) * numProg ( 14 , 29 )) |
| #У исполнителя Удвоитель две команды, которым присвоены номера: |
| #1. Прибавить 1 |
| #2. Умножить на 2 |
| #Сколько существует программ, преобразующих число 4 в число 24, предпоследней командой которых является команда «1»? |
| def numProg ( start , x ): |
| if start == x : |
| return 1 |
| if start > x : |
| return 0 |
| if start < x : |
| return numProg ( start + 1 , x ) + numProg ( start * 2 , x ) |
| print ( numProg ( 4 , 11 ) + numProg ( 4 , 22 )) |
| #1)Итак, мы знаем предпоследнюю команду – 1, при этом последняя команда может быть любая – 1 или 2, |
| #выходит, что нужно получить количество всех программ вида «*11» и «*12», где звёздочка обозначает любые команды |
| #2)Если программа заканчивается на «11», то до выполнения цепочки «11» у нас было число 24 – 1 – 1 = 22; |
| #поэтому нужно найти число программ для преобразования 4 в 22 |
| #3)Теперь рассматриваем случай, когда программа заканчивается на «12», это значит, что до выполнения цепочки «12» |
| #у нас было число (24/ 2) – 1 = 11; поэтому нужно найти число программ для преобразования 4 в 11 |
| #У исполнителя Калькулятор две команды, которым присвоены номера: |
| #1. прибавь 1 |
| #2. увеличь число десятков на 1 |
| #Например: при помощи команды 2 число 23 преобразуется в 33. Если перед выполнением команды 2 вторая с конца цифра равна 9, она не изменяется. |
| #Сколько есть программ, которые число 11 преобразуют в число 27? |
| def numProg ( start , finish ): |
| if start == finish : |
| return 1 |
| if start > finish : |
| return 0 |
| if start < finish : |
| return numProg ( start + 1 , finish ) + numProg ( start + 10 , finish ) |
| print ( numProg ( 11 , 27 )) |
| #У исполнителя Калькулятор две команды, которым присвоены номера: |
| #1. прибавь 1 |
| #2. увеличь каждый разряд числа на 1 |
| #Например, число 23 с помощью команды 2 превратится в 34, а 29 в 39 (так как младший разряд нельзя увеличить). |
| #Если перед выполнением команды 2 какая-либо цифра равна 9, она не изменяется. Сколько есть программ, |
| #которые число 25 преобразуют в число 51? |
| def com2 ( n ): |
| if n % 10 == 9 : |
| n += 10 |
| return n |
| else : |
| n += 11 |
| return n |
| def numProg ( start , finish ): |
| if start == finish : |
| return 1 |
| if start > finish : |
| return 0 |
| if start < finish : |
| return numProg ( start + 1 , finish ) + numProg ( com2 ( start ), finish ) |
| print ( numProg ( 25 , 51 )) |
| #Исполнитель U18 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера: |
| #1. Вычесть 1 |
| #2. Вычесть 3 |
| #3. Разделить нацело на 3 |
| #При выполнении команды 3 выполняется деление нацело (остаток отбрасывается). |
| #Программа для исполнителя U18 – это последовательность команд. Сколько существует таких программ, |
| #которые исходное число 22 преобразуют в число 2? |
| def numProg ( start , finish ): |
| if start == finish : |
| return 1 |
| if start < finish : |
| return 0 |
| if start > finish : |
| return numProg ( start — 1 , finish ) + numProg ( start — 3 , finish ) + numProg ( start // 3 , finish ) |
| print ( numProg ( 22 , 2 )) |
| #Исполнитель U18 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера: |
| #1. Вычесть 1 |
| #2. Вычесть 3 |
| #3. Взять остаток от деления на 4 |
| #Команда 3 выполняется только для чисел, больших, чем 4. |
| #Программа для исполнителя U18 – это последовательность команд. Сколько существует таких программ, |
| #которые исходное число 22 преобразуют в число 2? |
| def com3 ( n ): |
| if n > 4 : |
| n %= 4 |
| return n |
| else : |
| return 0 |
| def numProg ( start , finish ): |
| if start == finish : |
| return 1 |
| if start < finish : |
| return 0 |
| if start > finish : |
| return numProg ( start — 1 , finish ) + numProg ( start — 3 , finish ) + numProg ( com3 ( start ), finish ) |
| print ( numProg ( 22 , 2 )) |
Реальный вариант ЕГЭ по информатике 2022 №23
Информатика ЕГЭ задание 23 Тренировочный вариант №17 от 19.04.2021 «ЕГЭ 100БАЛЛОВ»
Sign up for free to join this conversation on GitHub. Already have an account? Sign in to comment
Источник: gist.github.com
Ещё пример задания:
Р-05. У исполнителя Удвоитель две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Удвоитель – это последовательность команд. Сколько существует программ, преобразующих число 4 в число 24, предпоследней командой которых является команда «1»?
- итак, мы знаем предпоследнюю команду – 1, при этом последняя команда может быть любая – 1 или 2
- выходит, что нужно получить количество всех программ вида «*11» и «*12», где звёздочка обозначает любые команды
- если программа заканчивается на «11», то до выполнения цепочки «11» у нас было число
24 – 1 – 1 = 22; поэтому нужно найти число программ для преобразования 4 в 22
- для начального числа 1 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды; если через
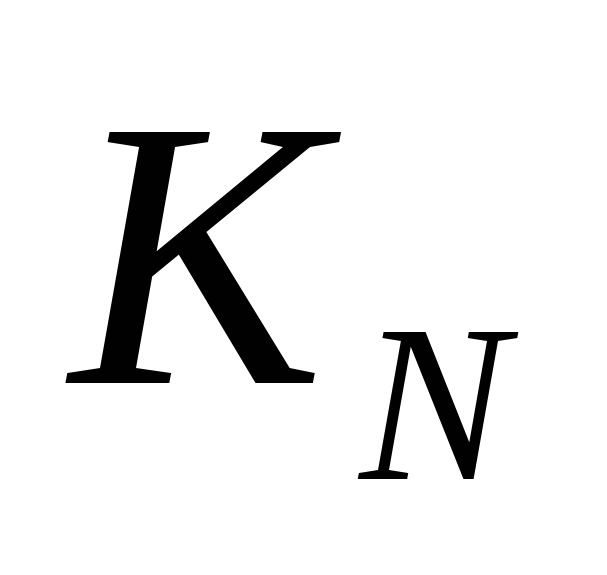 обозначить количество разных программ для получения числаNиз начального числа 1, то
обозначить количество разных программ для получения числаNиз начального числа 1, то 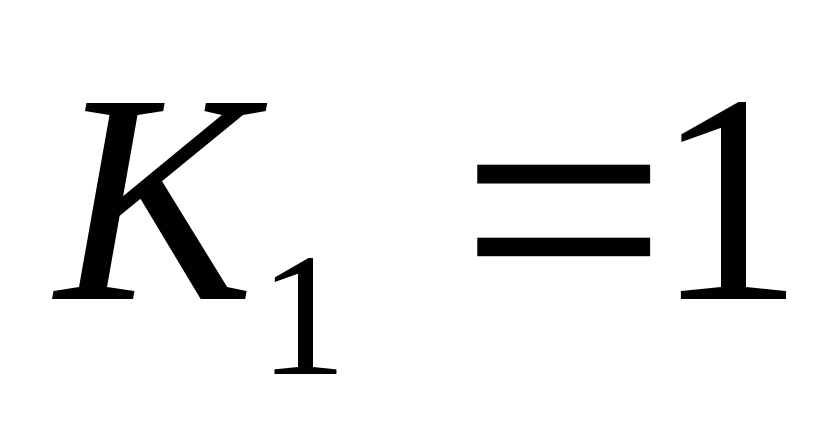 .
. - теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую
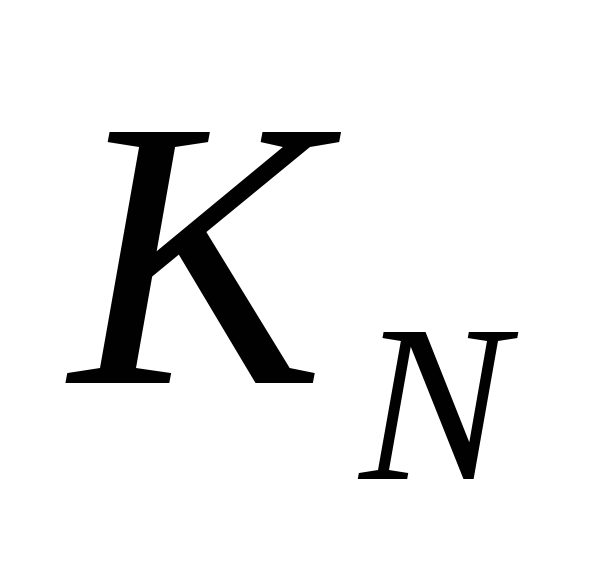 с предыдущими элементами последовательности
с предыдущими элементами последовательности 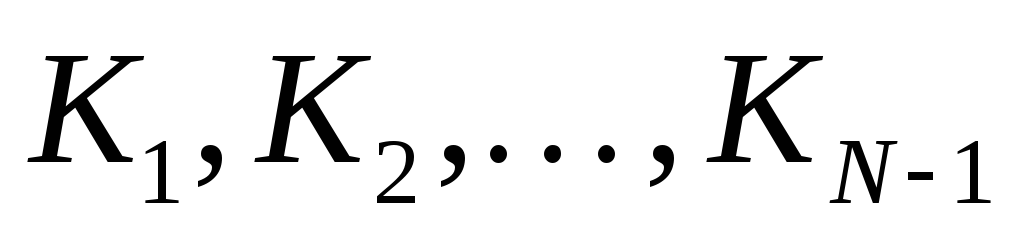 , то есть с решениями таких же задач для меньших N
, то есть с решениями таких же задач для меньших N - число Nмогло быть получено одной из двух операций:
- увеличением на 1 числа N-1;
- умножением на 2 числа N/2 (только для N, которые делятся на 2, и таких, что N/2 4);
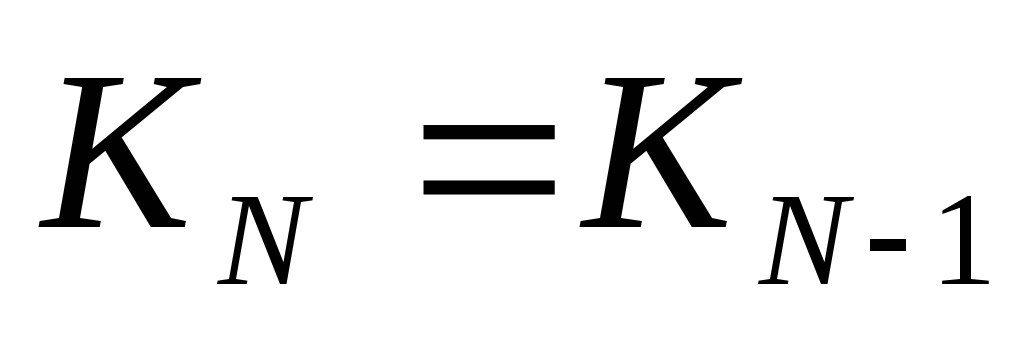 для нечётных чисел
для нечётных чисел 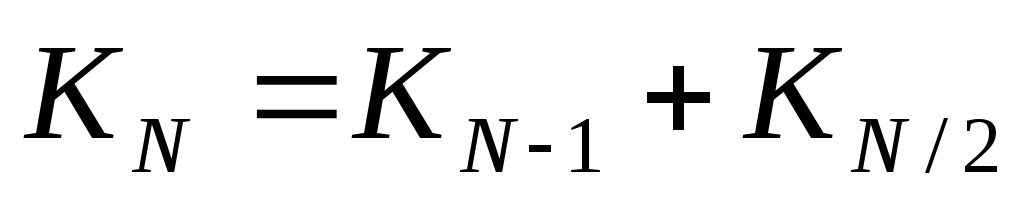 для чётных чисел, таких, что N/24
для чётных чисел, таких, что N/24
- составляем таблицу:
N 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 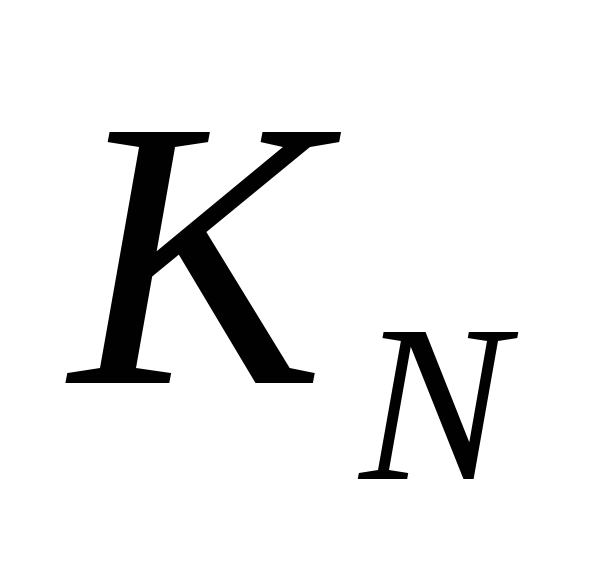
1 1 1 1 2 2 3 3 4 4 5 5 7 7 9 9 12 12 15 - теперь рассматриваем случай, когда программа заканчивается на «12», это значит, что до выполнения цепочки «12» у нас было число (24/ 2) – 1 = 11; поэтому нужнонайти число программ для преобразования 4 в 11, берём его из таблицы:3
- ответ к задаче – сумма двух значений, выделенных жёлтым маркером: 15 + 3 = 18, поскольку мы рассмотрели все варианты программ, в которых предпоследняя команда – 1
- Ответ: 18.
Ещё пример задания:
Р-04. Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений содержит число 10? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17. Решение:
- заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться)
- для начального числа 1 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды; если через
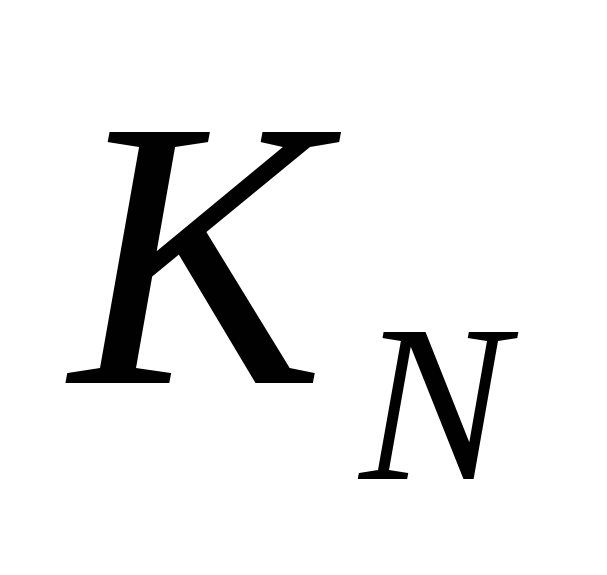 обозначить количество разных программ для получения числаNиз начального числа 1, то
обозначить количество разных программ для получения числаNиз начального числа 1, то 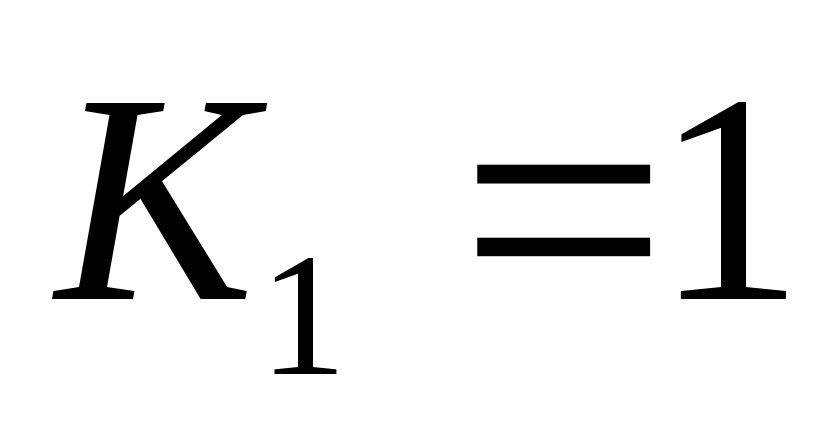 .
. - теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую
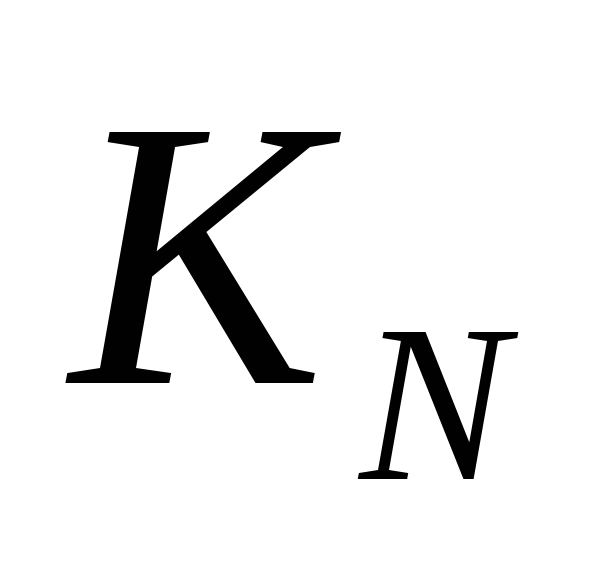 с предыдущими элементами последовательности
с предыдущими элементами последовательности 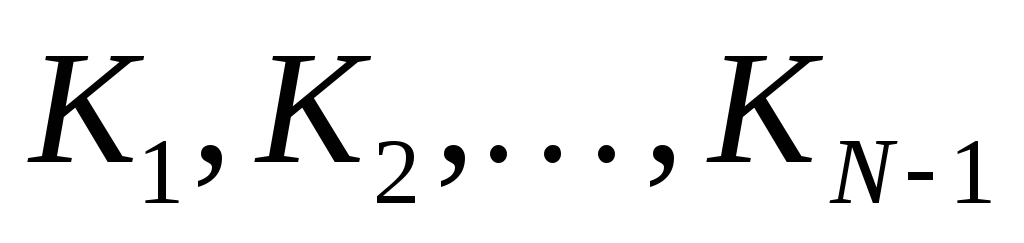 , то есть с решениями таких же задач для меньших N
, то есть с решениями таких же задач для меньших N - число Nмогло быть получено одной из двух операций:
- увеличением на 1 числа N-1;
- умножением на 2 числа N/2 (только для N, которые делятся на 2);
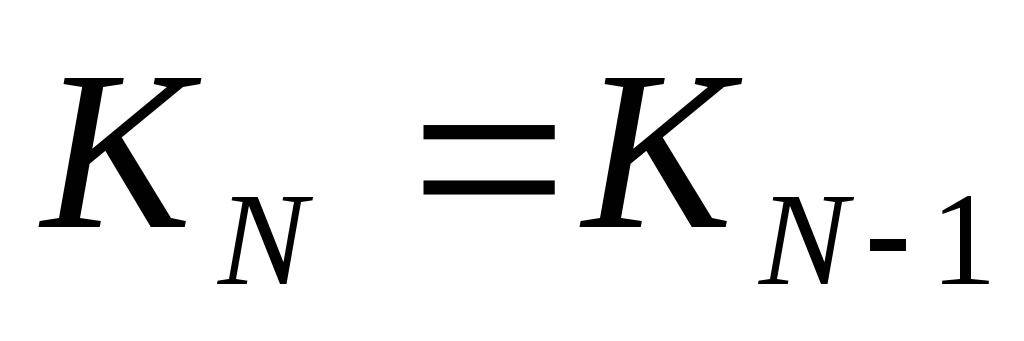 для нечётных чисел
для нечётных чисел 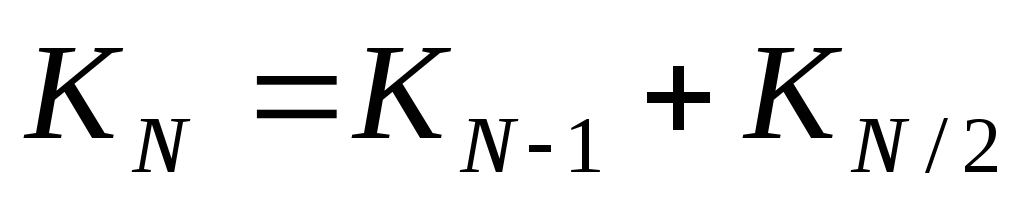 для чётных чисел
для чётных чисел
- поскольку траектория должна проходить через число 10, сначала выясняем, сколькими способами можно получить 10 из 1, а затем будем считать, сколько есть способов получить 21 из 10
- заполняем таблицу от 1 до 10 по полученным формулам:
N 1 2 3 4 5 6 7 8 9 10 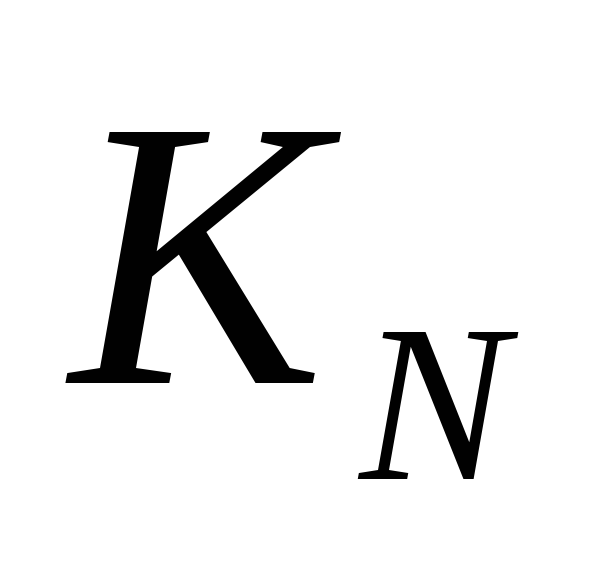
1 2 2 4 4 6 6 10 10 14 - второй этап – определяем таким же образом (и по таким же формулам!), сколько есть способов получить конечное число 21 из 10, только левую часть таблицы (от 1 до 10) мы уже не рассматриваем:
N 10 11 12 13 14 15 16 17 18 19 20 21 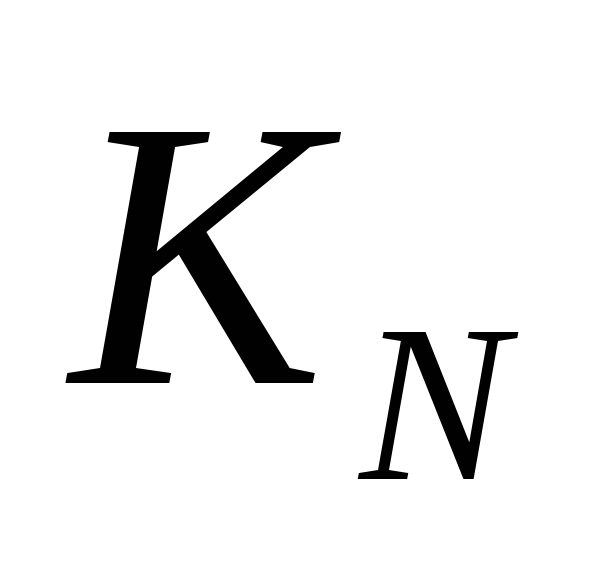
14 14 14 14 14 14 14 14 14 14 28 28 - Ответ: 28.
Источник: studfile.net
Понятная информатика,


(теория к урокам и ЕГЭ, задание 22).
Динамическое программирование – это способ или техника решения сложных задач путем приведения их к более простым подзадачам того же типа.
Динамическое программирование позволяет решать задачи, которые требуют полного перебора вариантов. Задание может звучать так:
- «подсчитайте количество способов…»;
- «как оптимально распределить…»;
- «найдите оптимальный маршрут…».
Динамическое программирование позволяет увеличить скорость выполнения программы за счет эффективного использования памяти; полный перебор всех вариантов не требуется, поскольку запоминаются и используются решения всех подзадач с меньшими значениями параметров.
Пример 1.
1. У исполнителя Калькулятор две команды, которым присвоены номера:
Сколько есть программ, которые число 1 преобразуют в число 55?
Обозначим через N текущее (получаемое) число, а через K(N) – количество различных программ для получения этого числа.
Число N может быть получено одной из двух операций:
— увеличением на 1 числа N-1 (предыдущего числа);
— умножением на 4 числа N/4 (только для N, которые делятся на 4).
Тогда получаем следующие рекуррентные формулы:
K(N)= K(N-1) — для чисел, не кратных 4;
K(N) =K(N-1) +K(N/4) — для чисел, кратных 4.
Заполним таблицу получения чисел от 1 до 55, указывая в ней только кратные 4 числа, так как числа, лежащие в промежутке между ними всегда равны предыдущему значению для кратного числа:
Здесь при N = 4 получаем K4=К3+К4/4= К3+К1=1+1=2;
N = 8 получаем K8=К7+К4/2= К4+К2 =2+1=3, и так далее.
А если посмотреть внимательно, то можно и сделать еще быстрее: так как числа кратны 4, то каждое увеличение выполняется по 4 раза (13 1, по 2, по 3…)
Пример 2.
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений содержит число 10?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Число N могло быть получено одной из двух операций:
— увеличением на 1 числа N-1;
— умножением на 2 числа N/2 (только для N, которые делятся на 2);
K(N) = K(N-1) — для нечётных чисел
K(N) = K(N-1) + К(N/2) — для чётных чисел
Поскольку траектория должна проходить через число 10, сначала выясняем, сколькими способами можно получить 10 из 1, а затем будем считать, сколько есть способов получить 21 из 10
Заполняем таблицу от 1 до 10 по полученным формулам:

Второй этап – определяем таким же образом (и по таким же формулам!), сколько есть способов получить конечное число 21 из 10, только левую часть таблицы (от 1 до 10) мы уже не рассматриваем:

На втором этапе можно использовать и такую идею: если мы знаем количество команд, с помощью которых из начального числа 1 можно получить 10 и определим количество команд, с помощью которых из 10 можно получить конечное значение 21, останется только перемножить эти два числа – это и будет ответ
Составляем таблицу для получения 21 из 10, используя те же рекуррентные формулы:

Результат : 14 * 2 = 28
Пример 3.
Исполнитель М17 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая – увеличивает его на 2, а третья – умножает его на 3. Программа для исполнителя М17 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 12 и при этом траектория вычислений содержит числа 8 и 10?
Запишем рекуррентную формулу для вычисления K(N) – количества возможных программ для получения числа N из некоторого начального числа:
K(N) = K(N-1) +К(N-2), если N не делится на 3
K(N) = K(N-1) +К(N-2) +К(N/3), если N делится на 3
Все допустимые программы можно разбить на 3 части:
– переход от 2 до 8
– переход от 8 до 10
– переход от 10 до 12

Обозначим через К(a->b) количество возможных программ получения числа b из числа a
Очевидно, что К(a->b) = К(a->c) * К(c->b) для любого c, такого что a < c < b
Поэтому К(2->12) = К(2->8) * К(8->10) * К(10->12)
Вычисляем эти значения отдельно стандартным способом по рекуррентным формулам п. 1:

и перемножаем: 15 × 2 × 2 = 60
Пример 4.
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 29 и при этом траектория вычислений содержит число 14 и не содержит числа 25?
В этом задании две особые точки – числа 14 (через которое должна проходить траектория) и 25 (а сюда она попасть НЕ должна)
Сначала, так же, как и в задачах, рассмотренных выше, составляем рекуррентную формулу, по которой будем вычислять количество K(N) обозначить количество разных программ для получения числа N из начального числа:
Число N могло быть получено одной из двух операций:
— увеличением на 1 числа N-1;
— умножением на 2 числа N/2 (только для N, которые делятся на 2);
K(N) = K(N-1) — для нечётных чисел
K(N) = K(N-1) + К(N/2) — для чётных чисел
Для начального числа 2 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды; K(1) = 1.
Составляем таблицу до первой особой точки – числа 14:
Источник: xn--80adgdici4b.xn--p1acf
ЕГЭ информатика. Коды
k=0 a=[] for x in range(2*10**10, 4*10**10+1, 100000):
if x%7==0 and x%101!=0: if x%13!=0 and x%29!=0 and x%43!=0: k+=1 a.append(x)
print(a[0], k) #20000400000
- Тип 3. Хотя бы два нуля.
a=[int(x) for x in range(1,100+1)]
for i in range(len(a)): s=str(a[i]) if s.count(«0»)==2: k+=1 print(k)
- Пример решения (основа)
- На компьютере на файл навести и в самом низу Свойства файла (Вохможно это на английском) и там путь нажо копировать. Не забыть r.
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от −10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из пяти элементов: 6; 2; 9; –3; 6 — ответ: 4 11.
- r»C:Usersmikepy101bookdatatest.txt»
f=open(r»/storage/emulated/0/Compiler/py_3/17-1.txt») a=[int(x) for x in f] sumMax=-100 count=0 for i in range(len(a)-1):
if a[i]%3==0 or a[i+1]%3==0: count+=1 sumMax=max(sumMax, a[i]+a[i+1])
- Тип 3 Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 3, а их сумма делится на 5. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар.
f=open(r»/storage/emulated/0/Download/17.txt») a=[int(x) for x in f] count=0 sumMax=-100000 for i in range(len(a)-1):
if a[i]%3==0 or a[i+1]%3==0: if (a[i]+a[i+1])%5==0: count+=1 sumMax=max(sumMax, a[i]+a[i+1])
print(count, sumMax, ‘Ответ на пример 3’)
Тип 4. В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 117, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен. f=open(r»/storage/emulated/0/Download/17-2.Два различных элемента.txt») a=[int(x) for x in f] f.close() k=0 mx=0 for i in range(len(a)-1):
for j in range(i+1, len(a)): if (a[i]+a[j])%117==0: k+=1 mx=max(mx, a[i]+a[j])
print(k,mx) #Ответ 427120 19890
- Задание 22
- Укажите наименьшее из таких чисел x, при вводе которого алгоритм печатает сначала 3, а потом 2.
for x in range(1,1000):
i=x a = 0 b = 0 while x > 0: a+=1 if (b<(x%8)): b=x%8 x//=8 if a==3 and b==2: print(i) break
- Написан алгоритм. Найдите при каком наибольшем х алгоримт напечатает сначала 6, а потом 13.
for x in range(10000001,1000000000,100): #единица в конце первого числа и шаг в 100 сделаны чисто чтоьы ускорить ппоцесс. Алгоритм работает и без них
a=0 i=x b=1 while x>0: a+=2 b*=(x%1000) x//=1000 if a==6 and b==13: print(i) #13001001 Ответ большой и выводится долго и от большого числа, поэтому при решении подобных задач не надо торопиться
- Получив на вход число x, этот алгоритм печатает два числа L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 25, а потом 3.
for i in range(400,1000):
l=0 step=0 m=1 x=i step=0 while x>0: l+=1 if x%2>0: m=x%8*m x//=8 step+=1 if step>1000: break if m==25 and l==3 and step
- Получив на вход число x, этот алгоритм печатает два числа a и b. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 12.
for i in range(1000,10000):
x=i a=0 b=1 while x>0: if x%2>0: a+=x%8 else: b=b*(x%8) x//=8 if a==2 and b==12: print(i) #3209 ответ
- Задание 22
- Укажите наименьшее возможное значение x, при вводе которого программа выведет сначала 3, а потом 2.
for i in range(1,100): x=i a=b=0 while x>0: if x%2==0: a+=1 else: b+=1 x//=2 if a==3 and b==2: print(i) #Ответ: 17.
- Получив на вход натуральное число x, этот алгоритм печатает число S. Укажите такое наименьшее число x, при вводе которого алгоритм печатает пятизначное число.
for i in range(1,10000):
x=i s=x R=0 while x>0: d=x%2 R=10*R+d x//=2 s=s+R if 1
- Тип количество цифр. #Получив на вход натуральное число x, этот алгоритм печатает число S. Укажите такое наименьшее число x, при вводе которого алгоритм печатает пятизначное число. #Аккауратно! строка x//=2 может быть написана в задании криво, но она должна быть под while
for i in range(15,20):
x=i s=x R=0 while x>0: d=x%2 R=10*R+d x//=2 s=s+R if s>=10000: print(i) #Ответ 17
- Задание 23
- Больше типов в Галерее
- Тип 1. Количество программ
Исполнитель Осень16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1) Прибавить 1; 2) Прибавить 2; 3) Прибавить 3. Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 3. Программа для исполнителя Осень16 — это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
if curr>end: return 0 if curr==end: return 1 if curr
print(f(1,8)*f(8,15)) #Ответ 1936
- Тип 2. Количество программ с избегаемым этапом
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера: 1. прибавь 1 2. сделай нечётное Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24?
if curr>end or curr==24: return 0 if curr==end: return 1 if curr
print(f(1,25)) #Ответ 10
- Тип 3. Количество программ с обязательным и избегаемым этапами.
Исполнитель РазДваТри преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 1 2. Прибавить 2 3. Умножить на 3 Сколько существует программ, которые преобразуют исходное число 1 в число 15, и при этом траектория вычислений содержит число 10 и не содержит числа 13? def f(curr,end):
if curr>end or curr==13: return 0 if curr==end: return 1 if curr
print(f(1,10)*f(10,15)) #Ответ 168
Тип 4. Исполнитель Увеличитель345 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера: 1. Прибавь 3 2. Прибавь 4 3. Прибавь 5 Первая из них увеличивает число на экране на 3, вторая увеличивает это число на 4, а третья – на 5. Программа для исполнителя Увеличитель345 – это последовательность команд. Сколько есть программ, которые число 22 преобразуют в число 42? def f(curr,end):
if curr>end: return 0 if curr==end: return 1 if curr
print(f(22,42)) #Ответ 73
Тип 5. Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: 1. Удвоить 2. Удвоить и прибавить Первая команда умножает число на экране на 2, вторая — умножает его на 2, а затем прибавляет 1. Сколько различных результатов можно получить из исходного числа 1 после выполнения программы, содержащей ровно 10 команд?
d=set() def f(curr,step):
if step==10: d.add(curr) else: f(curr*2, step+1) f(curr*2+1, step+1)
f(1,0) print(len(d)) #Ответ 1024
Тип 6. Предпоследняя команда. Две операции: 1)Прибавить 1 2)Прибавить 2 Сколько существует программ, которые преобразт число 3 в 18 и предпоследняя команда 2)? Предпоследняя команда это команда прибавления 2. Мы должны получить 18, т е это надо вычитать, получаем 15 и 14. Так как предпоследняя команда 2 переводит 15 в 17, а 14 в 16 и из них уже последней командой можно получить 18. def f(curr,end):
if curr>end: return 0 if curr==end: return 1 if curr
print(f(1,14)+f(1,15)) #Ответ 987
Тип 7. Самая короткая программа. Три команды: Прибавить 1 Прибавить 5 Умножить на 3 Найдитe длину самой короткой программы, которая преобразует 1 в 227.
if curr>end: return 10**8 if curr==end: return step if curr
print(f(1,227,0)) #Ответ 7
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). В строках, содержащих менее 25 букв A, нужно определить и вывести максимальное расстояние между одинаковыми буквами в одной строке. Пример.
Исходный файл: GIGA GABLAB NOTEBOOK AGAAA В этом примере во всех строках меньше 25 букв A. Самое большое расстояние между одинаковыми буквами – в третьей строке между буквами O, расположенными в строке на 2-й и 7-й позициях. В ответе для данного примера нужно вывести число 5.
f=open(r’/storage/emulated/0/Download/inf_26_04_21_24.txt’) alf =[«A», «B», «C», «D»,»E»,»F»,»G»,»H»,»I»,»J»,»K»,»L»,»M»,»N»,»O»,»P»,»Q»,»R»,»S»,»T»,»U»,»V»,»W»,»X»,»Y»,»Z»] ss=f.readlines() m=-1 for s in ss:
if s.count(«A»)>=25: continue for c in s: if s.count(c)>1: m = max(m, s.rfind(c) — s.find(c)) j=c
print(m, j) #Ответ 1004 N
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z).
Необходимо найти строку, содержащую наименьшее количество букв N (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите. Пример.
Исходный файл: NINA NABLAB ANAAA В этом примере в первой строке две буквы N, во второй и третьей — по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
f=open(r»/storage/emulated/0/Download/24-2-пример 2 задание 24.txt») s=f.readline() mn=1000 m=0 for s in f:
k=0 for i in range(len(s)): if s[i]==»N»: k+=1 if km: ch=s[i] m=curch
print(mn,ch) #Ответ 23 Y
from collections import Counter
word = ‘приоритет’ c = Counter(word) print(c.most_common(1)[0][0])
Т.к. метод most_common возвращает список самых частых значений (даже если мы запросили одно самое частое значение), то нужно взять первый элемент (для этого нужен первый [0]). Каждый элемент в этом списке — пара (элемент, количество), поэтому нужно взять первый элемент еще раз.
Вообще, в слове «приоритет» есть 3 буквы, которые встречаются по два раза (р, и, т), выведет только одну из них (у меня вывело «р»).
from collections import Counter f=open(r»/storage/emulated/0/Download/24-2-пример 2 задание 24.txt») s=f.readline()+»*» h=[] m=10000 for s in f:
k=0 for i in range(len(s)): if s[i]==»N»: k+=1 if k
print(m, c.most_common(24)[0][0]) #реже всего print(m, c.most_common(24)[-1][0])
- Ответ 23, Y
- Вообще. Можно сделать и так:
from collections import Counter f=open(r»/storage/emulated/0/Download/24-2-пример 2 задание 24.txt»)
s=[«N»]*10000 lines=f.readlines() for line in lines:
if line.count(«N»)
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Определите количество строк, в которых буква E встречается чаще, чем буква A. Для выполнения этого задания следует написать программу.
Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
f=open(r»/storage/emulated/0/Download/inf_22_10_20_24.txt») k=0 for s in f:
if s.count(«E»)>s.count(«A»): k+=1
print(k) #Ответ 467
Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы A.
Например, в тексте ABCAABADDD после буквы A два раза стоит B, по одному разу — A и D. Для этого текста ответом будет B.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
f=open(r»/storage/emulated/0/Download/24-какая буква чаще после А.txt») s=f.readline() m=0 mch=»» for i in range(ord(«A»), ord(«Z»)+1):
ch=chr(i) k=0 for i in range(len(s)-1): if s[i]==»A» and s[i+1]==ch: k+=1 if k>m: m=k mch=ch
Источник: www.wikiznanie.ru