Структурная схема алгоритма программы

Определение алгоритма. Структурная схема алгоритма. Виды блоков структурной схемы. Их назначение согласно ГОСТ. Правила построения структурной схемы алгоритма.

Линейная, разветвляющаяся и циклическая структуры алгоритмов.

Алгоритм и его свойства

В основе решения любой задачи лежит понятие алгоритма. Под алгоритмом принято понимать “точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату” (ГОСТ 19.781-74).

При составлении алгоритмов следует учитывать ряд требований, выполнение которых приводит к формированию необходимых свойств.

Алгоритм должен быть однозначным, исключающим произвольность толкования любого из предписаний, и заданного порядка исполнения. Это свойство алгоритма называется определенностью.

Реализация вычислительного процесса должна через определенное число шагов привести к выдаче результатов или сообщения о невозможности решения задачи. Это свойство алгоритма называется результативностью.

Блок схема алгоритма (часть 1)

Решение однотипных задач с различными исходными данными можно осуществлять по одному и тому же алгоритму, что дает возможность создавать типовые программы для решения задач при различных вариантах задания значений исходных данных. Это свойство алгоритма называется массовостью.

Предопределенный алгоритмом вычислительный процесс можно расчленить на отдельные этапы, элементарные операции. Это свойство алгоритма называется дискретностью.

Алгоритмизация — техника составления алгоритмов и программ для решения задач на ЭВМ.

Изобразительные средства для описания алгоритмов

К изобразительным средствам описания алгоритмов относятся следующие основные способы их представления:

а) словесный (записи на естественном языке);

б) структурно — стилизованный (записи на языке псевдокода);

в) программный (тексты на языках программирования);

г) графический (схемы графических символов).

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных и задается в произвольном изложении на естественном языке. Способ основан на использовании общепринятых средств общения между людьми и с точки зрения написания трудностей для авторов алгоритмов не представляет. Однако для “исполнителей” такие описания алгоритмов часто неприемлемы. Они строго не формализуемы, страдают многословностью записей, допускают неоднозначность толкования отдельных предписаний. Поэтому такой способ описания алгоритмов не имеет широкого распространения.

1) если числа равны, то необходимо взять любое из них в качестве ответа, в противном случае — продолжить выполнение алгоритма;

2) определить большее из чисел;

3) заменить большее число разностью большего и меньшего чисел;

4) повторить алгоритм с начала.

Структурно — стилизованный способ записи алгоритмов основан на формализованном представлении предписаний, задаваемых путем использования ограниченного набора типовых синтаксических конструкций. Такие средства описания алгоритмов часто называются псевдокодами. Разновидностью структурно-стилизованного способа описания алгоритмов является алгоритмический язык в русской нотации (АЯРН).

Схема алгоритма

Приведем описанный на таком языке алгоритм решения задачи об определении принадлежности точки D треугольнику АВС.

Источник: studopedia.su

Составление структурных схем алгоритмов и программ

Пример 1

Автомобиль едет со скоростью V=85 км/ч. Какой путь он пройдет за T=3ч? Решение Любой алгоритм начинается с того, что нам дано (или должно быть дано) для решения задачи. Так как мы ищем путь по формуле S=V•T, то для вычисления S надо знать V и T. Они нам даны по условию задачи.

Перед составлением любого алгоритма необходимо заранее все привести к единым единицам измерения, т.е., например, либо все временные величины измерять в часах, либо в минутах и т.д. В алгоритме единицы измерения опускаются. Имена всех переменных в алгоритме будем писать большими буквами. В каждом пункте алгоритма должна выполняться только одна операция.

Знак умножения проставляется символом «*» («звездочка»). Составим описательный алгоритм: < 1) Дано: V=85 2) T=3 3) Что можно вычислить, используя заданные исходные данные? S=V*T 4) Задачу мы решили. Путь определен. Если мы по составленному алгоритму напишем программу, то ЭВМ вычислит S и будет знать результат.

А для того, чтобы и мы его узнали, результат надо либо распечатать на бумаге, либо вывести его на экран монитора  Вывод: S. 5) Конец. Для того чтобы не описывать алгоритм вот так, словами, и он мог быть понятен каждому человеку, занимающемуся программированием, введен единый язык описания алгоритмов — язык структурных схем алгоритмов и программ.

Для построения схем используются специальные блоки (называемые также символами). Рассмотрим некоторые блоки и правила составления схем алгоритмов и программ. Указанные ниже размеры блоков соответствуют широко распространенным специальным линейкам, предназначенным для вычерчивания структурных схем алгоритмов и программ.

Для составления схем используются следующие блоки: 1)ПРОЦЕСС (см. рис. 2) Предназначен для присваивания значений переменным Рис. 2 Символ ПРОЦЕСС 2) РЕШЕНИЕ (см. рис. 3) Предназначен для проверки условия Рис.

3 Символ РЕШЕНИЕ 3) ВВОД-ВЫВОД (см. рис. 4) Рис. 4 Символ ВВОД-ВЫВОД 4)ПУСК-ОСТАНОВ (см. рис. 5) (начало-конец) 30 Рис. 5 Символ ПУСК-ОСТАНОВ 5)МОДИФИКАЦИЯ (см. рис. 6) Предназначен для организации цикла Рис.

6 Символ МОДИФИКАЦИЯ 6) ПРЕДОПРЕДЕЛЕННЫЙ ПРОЦЕСС (см. рис. 7) Предназначен для обращения к под- программам Рис. 7 Символ ПРЕДОПРЕДЕЛЕННЫЙ ПРОЦЕСС Блоки в структурных схемах записываются в столбик и соединя­ются между собой линиями потока. Длина линии потока между блоками равна 1 см.

Блок «КОНЕЦ» располагается под блоком «НАЧАЛО». Кроме того, блоки нумеруются, за исключением блоков «ПУСК-ОСТАНОВ». Например (см. рис. 8): В

нутри блока можно записывать только одну операцию. Все блоки имеют только один вход — сверху и один выход — снизу. Исключение составляет блок «РЕШЕНИЕ».

У него всегда один вход, но два выхода, обозначающиеся со стрелками. Один выход – «да», другой – «нет». В Рис. 8 Фрагмент оформления структурной схемы ыход «да» обозначается единицей — 1 — и направлен (по ГОСТам) вниз, «нет» — обозначается нулем –Ø — и направлен вправо.

Ноль перечеркивается, чтобы отличить его в тексте алгоритма или программы от буквы О. Текст в блоках записывается шрифтом. Все математические знаки операций проставляются. Блок «ВВОДА-ВЫВОДА» один и тот же, поэтому, если он предназначен для ввода, то вверху, внутри блока, пишут «Ввод:», если для вывода – «Вывод:» (см. рис. 9).

Ввод: Вывод: Рис. 9 Примеры оформления символов «ВВОДА-ВЫВОДА» В структурных схемах допускается записывать комментарий, который обозначается следующим образом (см. рис. 10). здесь записывается комментарий Рис.

10 Пример оформления комментариев в структурных схемах Если структурная схема не помещается в один столбик, то рядом организовывают второй столбик или делают перенос на другую страницу. Перенос на эту же страницу в другой столбик осуществляется двумя способами (см. рис. 11). 1

) 2) Рис.

11 Два способа переноса структурных схем на одной странице Диаметр кружка – 1 см. Линии потока могут изгибаться только под прямым углом, располагаться от символов на расстоянии не менее 5 мм и не могут пересекаться между собой. Стрелки на линиях потока не ставятся, если линии идут сверху вниз или слева направо.

В противном случае направление обозначается стрелкой: . Стрелки ставятся при переходе на следующую страницу или в новый столбик. Перенос на другую страницу осуществляется следующим образом: пусть нам надо осуществить перенос с четвертой страницы с шестого блока на пятую страницу на блок № 9 (см. рис. 12).

На текущей странице №4: На странице № 5 1 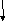Рис. 12 Перенос структурных схем на другую страницу Размеры символа, предназначенного для переноса структурной схемы на другую страницу, представлены на рисунке 13.

12 Рис. 13 Размеры символа переноса структурных схем на другую страницу Если переход на некоторый блок осуществляется из нескольких мест алгоритма, то в схеме этот переход (слияние) обозначают так, как показано на рисунке 14.

в середину линии потока Рис. 14 Слияние линий потока в структурных схемах При слиянии нескольких линий потока вливающиеся линии отмечаются стрелками.

Теперь, используя описанные выше правила, составим структурную схему для решения нашей задачи о вычислении пути (см. рис. 15). Рис. 15 Структурная схема для задачи вычисления пройденного пути Запомните, что исходные данные — это конкретные числа, значения некоторых переменных. Sin, Cos и т.д. — это имена функций, а не данные, т.е.

Sin x — это выражение, но не данное. Для того чтобы найти значение выражения, например, Sin x, нам нужно знать данное х. И еще одно. При присваивании слева от знака равенства стоит та величина, которую мы ищем, т.е. только лишь имя переменной, а не выражение. Справа — может стоять и имя переменной, и число, и выражение.

Но значения всех переменных, стоящих справа от знака равенства, должны быть известны, т.к., например, если мы не будем знать, чему равен Х при вычислении значения Y: Y = Sin X, то никогда не вычислим Sin Х и, следовательно, не найдем Y. В “ячейку” ЭВМ с именем Y нечего будет помещать. И еще одно правило надо запомнить. При составлении структурных схем и программ мы с Вами будем стремиться минимизировать количество операций и заводить как можно меньше переменных, т.е. минимизировать время счета и использование памяти ЭВМ. Таким образом, ни одного лишнего знака и операции!

Источник: studfile.net

Структурные схемы алгоритмов

Структурные схемы представляют алгоритм в наглядной графической форме. Действия алгоритма помещаются внутрь блоков, соединенных стрелками, показывающими очередность выполнения действий алгоритма. Приняты определенные стандарты графических изображений функциональных блоков:

q действия ввода – вывода данных помещают в блоках, имеющих вид параллелограмма,

q действия обработки информации помещают в блоках, имеющих вид прямоугольников,

q команды проверки условий — в блоках, имеющих вид ромбов,

q начало и конец алгоритма обозначают овалом.

Структуры алгоритмов

Алгоритмы строятся из некоторых основных структур, состоящих из отдельных базовых элементов. Можно выделить три структуры (конструкции): линейная (последовательная), разветвляющаяся и циклическая.

Действие 1

Действие 2

Действие 3

Структура, состоящая из последовательности шагов (действий) называется линейной (см. рисунок 7.1). Каждый функциональный блок этой структуры имеет один вход и один выход.

Рисунок. 7.1. Линейная структура алгоритма

Структура, обеспечивающая выбор между двумя альтернативами в зависимости от исходных данных, называется разветвляющейся или условной. Различают полное (см. рисунок 7.2) и неполное (см. рисунок 7.3) ветвления. В этой структуре присутствует блок условия, который имеет один вход и два выхода (истина и ложь). После проверки условия на каждой ветви располагается линейная структура.

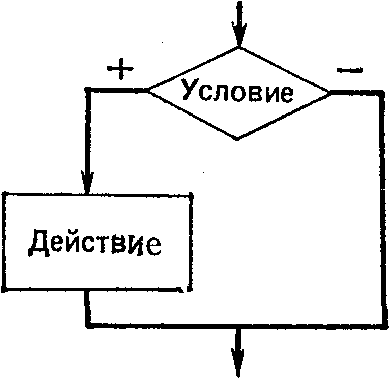
Рисунок 7.2. Полная форма ветвления Рисунок 7.3. Неполная форма ветвления

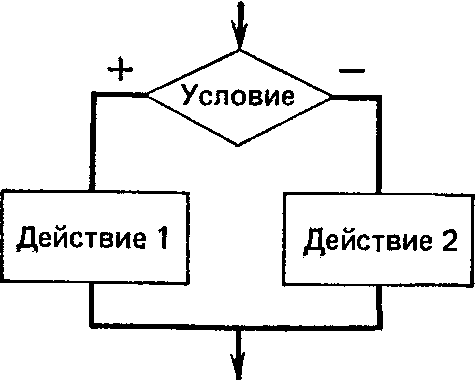
Структура, обеспечивающая повторение линейных и условных структур в зависимости от входных данных и условия задачи, называется циклической (или циклом). Различают циклы с предусловием (проверка условия стоит перед началом действий рисунок 7.4) и циклы с постусловием (проверка условия стоит после выполнения действий рисунок 7.5).

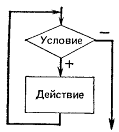
Рисунок 7.4. Цикл с предусловием Рисунок 7.5. Цикл с постусловием

Кроме перечисленных структур существуют подчиненные команды или процедуры, предназначенные для выполнения повторяющихся действий с разными входными данными. Пример структурной схемы приведен на рисунке 7.6.

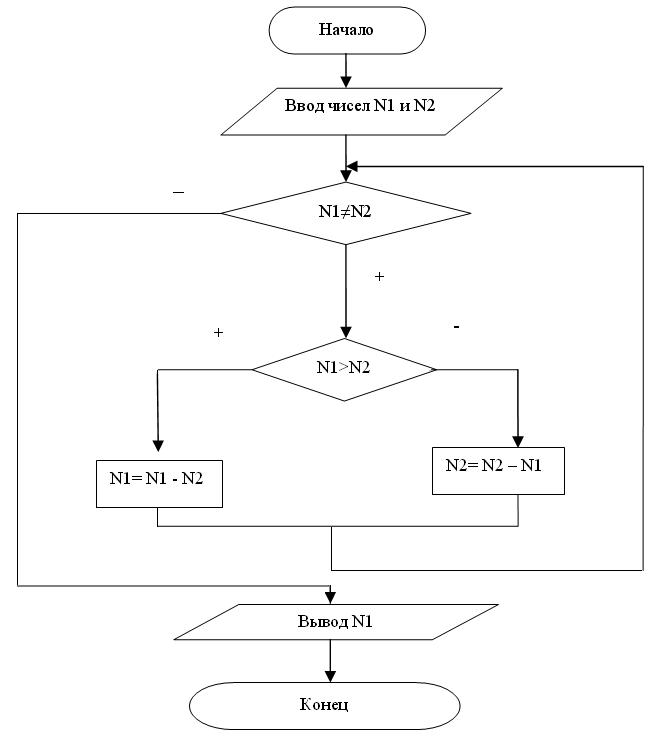
Рисунок 7.6. Пример структурной схемы алгоритма Евклида

Для записи внутри блоков действий используется естественный язык с элементами математической символики. В результате проверки условия возникают два возможных пути для продолжения алгоритма. Эти пути изображаются стрелками со знаками «+» и «-» (иногда пишут также «Да» и «Нет»).

Переход по стрелке со знаком «+» происходит, если условие истинно, а переход по стрелке «-», если условие ложно.

Схемы алгоритмов обладают большей наглядностью, чем словесная запись алгоритма. Однако эта наглядность быстро теряется при изображении большого алгоритма — в этом случае схема получается плохо обозримой.

При составлении алгоритмов следует учитывать начальные значения переменных, в которых будут накапливаться сумма или произведение, а также изменение переменной-индекса, т.е. порядкового номера значений последовательности чисел.

Задания:

Используя рассмотренные ранее структуры, создать следующие алгоритмы:

· Нахождение суммы последовательности чисел.

· Нахождение произведения последовательности чисел.

· Нахождение среднего значения последовательности чисел.

· Нахождение факториалов: n!, 2n. (2n+1)!! (раздельные алгоритмы и один – общий)

· Нахождение суммы всех положительных (отрицательных) чисел

· Нахождение максимального (минимального) значения последовательности чисел.

· Нахождение корней квадратного уравнения.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru