Один из методов улучшения программы является структурное программирование (СП). Оно предназначено для организации проектирования программ и процесса кодирования. Таким образом, чтобы предотвратить большинство логических ошибок и обнаружить те которые допущены.
Перечислим некоторые достоинства структурного программирования:
1. Структурное программирование позволяет значительно сократить число вариантов построения программы по одной и той же спецификации, что приводит к значительно снижает сложность программы.
2. В структурированных программах логически связанные операторы находятся визуально ближе, а слабо связанные дальше, что позволяет обходится без блок схем и других графических форм изображения алгоритмов.
3. Сильно упрощается процесс тестирования и отладки структурированных программ.
4. более высокую производительность работы за счет того, что действие каждой управляющей структуры хорошо известно и нет необходимости его обдумывать;
5. ясность и читаемость программ;
Язык программирования Си. Урок 1. Базовая структура программы
6. более высокую эффективность за счет глобальной оптимизации программы.
СП сосредотачивается на одном из наиболее подверженных ошибками факторов программирования – логики программы и включает три главные составляющие:
1. проектирование сверху – вниз (нисходящее проектирование) – подобно написанию статьи сверху — вниз. Процесс написания статьи имеет иерархическую структуру и начинается с вершины иерархии, т.е. с краткого обзора. Разработку проекта обычно начинают с исследования целей и определения основных задач, ведущих к достижению этих целей.
Если проект очень большой, то необходимо провести его разбиение. Вначале необходимо написать то, что вы хотите сделать на естественном языке. Этот шаг часто многое раскрывает. Нередко вы обнаружите, что не в состоянии записать задачу на естественном языке. В таком случае не надейтесь, что вам удастся составить программу.
Следовательно важно формулировать задачу правильно на стадиях проектирования, чтобы не исправлять ее позднее на стадиях программирования и отладки. Метод проектирования сверху — вниз предусматривает вначале определения задачи, а затем постепенное уточнение структуры путем внесения более мелких деталей.
Проектирование представляет собой последовательность шагов такого уточнения. На каждом шаге необходимо выявить функции, которые нужно воплотить, т.е. данная задача разбивается на ряд, каждому из них будет соответствовать один модуль.
Именно такой традиционный и по существу иерархический подход применяется при создании сложных структур в других областях (в технике, в серийном производстве). Далее следует описать данные указывая их структуру и основные процессы обработки.
Это описание должно включать тщательно отработанные примеры, убедительно демонстрирующие функции системы и их наиболее существенные варианты – такие примеры будут полезны позже на стадии тестирования. При описании модуля должны быть описаны его тестовые данные. Тестирование программы неизбежно, поэтому выявление требований к тестированию, заранее на стадиях проектирования, являются хорошей практикой. Логическая проверка фрагментов программы должна уменьшить необходимость тестирования конечной программы. Основное преимущество такого метода работы то, что он обеспечивает создание документации.
Уроки C# (Для новичков) #3 — Структура программы
2. модульное программирование. Чтобы преуспеть в структурном программировании программу следует представить в виде модулей. Модульное программирование – это процесс разделения программы на логические части, называемые модулями, и последовательное программирование каждой части. Когда большая единая задача делиться на подзадачи, то значительно проще прочесть и понять программу. Если проведено программирование всей задачи сверху – вниз, то она естественно разбивается на подзадачи для возможных модулей. При этом преследуется две цели:
необходимость добиться того, чтобы программный модуль был правильным и не зависел от контекста в котором он будет использоваться
следует стремиться к тому, чтобы из модулей можно было формировать большие программы без каких-либо предварительных значений о внутренней работе модуля.
Оптимальный размер модуля 60 строк.
Независимость. Следует стремиться к независимости между модулями или программами. Для достижения этого требуется, чтобы модуль не зависел от: 1) источника входных данных; 2) местоназначения выходных данных; 3) от пред — истории. При разбиении программы на функциональные блоки, независимые модули можно обеспечивать некоторую самостоятельность последних.
Хотя определенная зависимость все таки существует. Каждый модуль должен иметь свое назначение, отличающееся от назначения других модулей. Это должен быть замкнутый блок, вход и выход которого четко определены. Стремление к независимости хорошо тем, что менее вероятно, что изменения в одной подпрограмме влияет на оставшуюся часть программы.
Воздействие изменения в одном модуле на другую часть программы называется волновым эффектом. Этот эффект можно уменьшить сведя к минимуму связь между модулями, т.е. сократить количество путей вдоль которых изменения или ошибки могут проникнуть в другие части. Постой путь уменьшения волнового эффекта – избегать использование глобальных перемен и делать модуль небольшим.
Минимизация взаимосвязи между модулями – это модульное сцепление, которое происходит за счет усиления связей между элементами одного модуля (модульная прочность). Таким образом тесно связанные элементы надо стремиться поместить в один модуль. Использование модулей приводит к уменьшению сложностей, факторы сложности при этом включают три составляющие: 1) функциональная сложность – обусловлено тем, что один модуль выполняет слишком много функций; 2) распределенная сложность – это сложность идентификации общей функции распределенной между несколькими модулями за счет чего утрачивается возможность уменьшения сложности всей программы при модульном программировании; 3) сложность связи – определяется сложностью взаимодействия модулей, при использовании общих данных.
3. структурное кодирование – это метод написания хорошо структурированных программ, который позволяет получать программы более удобные для тестирования, модификации и использования. Программы произвольных размеров и сложности могут быть написаны на основе ограниченного множества базисных структур. Этот принцип положен в основу проектирования схем, где любая логическая структура может быть создана из элементарных структур:
структура последовательности – это формализация того, что операторы программы выполняются в порядке их появления в программе, пока что-то не изменит их последовательность.
структура выбора – это выбор одного из двух действий исходя из выполненного некоторого условия.
структура повторения – используется для повторного выполнения группы команд до тех пор, пока не выполниться некоторое условие. Получение правильной программы путем замены операторов программы на управляющие логические структуры называется вложением структур.
Структурирование.
В основу структурирования положены следующие простые правила:
1. программа должна составляться мелкими шагами, размер шага определяется количеством решений, применяемых программистом на этом шаге.
2. сложная задача разбивается на простые легко воспринимаемые части, каждая из которых имеет только один вход и один выход.
3. логика программы должна опираться на минимальное число простых базовых управляющих структур.
Фундаментом структурного программирования является теорема о структуризации. Эта теорема устанавливает, что как бы не была сложна задача, блок-схема программы может быть представлена с использованием весьма ограниченного числа элементарных управляющих структур. Эти элементарные структуры могут соединяться между собой, образуя более сложные структуры, при этом они могут представлять собой довольно сложные блок-схемы с одним входом и с одним выходом.
Чтобы обойтись без произвольных передач управления в программе, там где это возможно, лучше не использовать операторы GOTO, RETURN. Характерной особенностью структурированной программы является не столько отсутствие этих операторов, а сколько наличие жесткой структуры ее организации. Если текст программы будет занимать несколько десятков страниц, то восприятие такой программы будет затрудненно, поэтому рекомендуется вести структурирование текста программы (например, программа состоит из 80 страниц исходного текста, необходимо этот исходный текст заменить на текст в котором отражаются наиболее важные, в функциональном смысле, фразы в виде сегментов). Если расписать весь программный комплекс крупными сегментами, то описание всего комплекса может занять всего одну страницу, а это наглядно и удобно.
Графическое представление программных алгоритмов имеет широкое распространение благодаря наглядности. Граф-схема представляет собой граф, состоящий из вершин, соединенных направленными стрелками-дугами.
2. функциональный оператор –
3. условный или объединяющий операторы –
4. останов – конечный оператор
5. дуги, определяющие последовательность выполнения действий
Программа называется простой, если ее граф-схема удовлетворяет следующим условиям: 1) один вход и один выход, 2) через каждую ее вершину проходит хотя бы один путь от входа к выходу. Сложная программа обычно имеет больше, чем один вход или выход.
Если комплекс программ большой и блок-схема программы большая необходимо выделить в ней подграфы, достаточно простые и понятные по структуре.
Структурирование программных компонент. При иерархическом построении комплекса программ важное значение имеют объем, сложность компонент для каждого уровня иерархии. По принципам построения, языку описания, объему и другим характеристикам в структуре комплекса программ можно выделить следующие иерархические уровни:
операторов и операндов программ, соответствующих компонентам текста программ на языке программирования;
программных модулей, оформляемых, как законченные компоненты текста программ;
функциональных групп программ или пакета ПП;
комплекса программ, оформляемого как завершенное ПС определенного целевого назначения.
Восходящее и нисходящее проектирование. Многоуровневый иерархический подход позволяет проектировать сложные комплексы программ по принципу сверху – вниз с позиции назначения и наилучшего решения основной цели, задачи всей системы.
Иногда основному проектированию сверху – вниз сопутствует разработка компонент снизу – вверх. Разработка начинается с модулей нижнего уровня, далее переходят к разработке модулей следующего уровня и т.д. Достоинством этого принципа является то, что при переходе к разработке модулей более высокого уровня иерархии, модули нижних уровней можно считать готовыми и подключать их к модулям верхнего уровня на стадии отладки.
Общие правила структурного построения ПС. Если комплекс программ строится на основе модульно иерархической структуры, состоящей из программных и информационных модулей, то на начальных этапах разработки комплекса программ формируется его структура и общие правила взаимодействия компонент. Эти правила состоят в следующем:
1. правило связи программных модулей по управлению. Передача управления вызываемому модулю всегда осуществляется через первый оператор или команду, а выход из вызываемому модуля всегда происходит через его естественное окончание, т.е. через последний оператор или команду. По окончании испытания вызываемого модуля управление передается в вызывающий модуль на оператор, следующий непосредственно за оператором вызова. Модули нижних уровней или одного уровня иерархии могут вызываться для исполнения только модулями высших уровней, т.е. модули нижних уровней не могут вызывать модули высших уровней, а модули одного уровня – вызывать друг друга.
2. правило связи программных модулей по информации. Инф-ция зон глобальных переменных доступна для использования любыми модулями, входящих в комплекс программ или группу программ, в соответствии с областью действия зоны глобальных переменных, т.е. глобальные переменные могут быть доступны не для всего комплекса программ, а лишь для указанной в описании группы модулей.
Локальные переменные доступны лишь в пределах того модуля, в котором они определены. Для взаимодействия вызываемых и вызывающих модулей создаются зоны обменных переменных, инф-ция из которых доступна лишь модулям непосредственно связанных по управлению. Запрещается использование для обмена информацией между модулями регистры и ячейки памяти, используемые как регистры, т.е. после окончания работы вызываемого модуля считается, что регистры не содержат инф-ции. Инф-ция находящаяся в регистрах вызывающего модуля при вызове должна быть сохранена на период выполнения вызываемого модуля и восстановлена при возврате в вызывающий модуль.
3. типовая структура программного модуля. Под структурой программного модуля понимается совокупность смысловых частей, образующих модуль и используемых для различных целей при его разработке и использовании. Типовая структура модуля в общем случае включает: 1) заголовок; 2) описание переменных; 3) тело модуля; 4) точки входа и выхода.
Элементарные базовые структуры. Любую программу можно синтезировать на основе элементарных базовых конструкций трех типов:
1. простая вычислительная последовательность, заключается в преобразовании или перемещении совокупности исходных переменных. Элементарные конструкции следуют друг за другом, причем конец предыдущего оператора замыкается на начало последующего.
2. альтернатива состоит в проверке некоторого условия.
3. итерация представляет собой структуру, в которой при каждом обращении один из нескольких операторов повторяется более одного раза. Для структурирования программ число итераций должно быть задано до входа в цикл, а не определяться вычислениями внутри цикла. В результате чего исключается возможная неопределенность функционирования программы.
Простота исходных конструкций структурного программирования предотвращает появление сложных информационных связей и запутанных передач управления.
Структурированными считаются программы, которые не имеют циклов с несколькими выходами, не имеют переходов внутрь циклов или условных операторов и не имеют выходов из внутренней части циклов или условных операторов.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
5. Организация программ со структурой вложенных циклов
Структурой с вложенным циклом называют такую структуру, в которой внутри одного цикла находится один или несколько других циклов. Цикл, расположенный внутри другого цикла, называют внутренним. Цикл, внутри которого находятся другие циклы, называют внешним.
Таким образом, один и тот же цикл может выступать и в роли внешнего (если он содержит внутри себя другие циклы), и в роли внутреннего (если он расположен внутри другого цикла). Правильная организация вложенного цикла состоит в том, что внутренний цикл должен целиком располагаться внутри внешнего цикла . Допустимыми являются следующие варианты организации вложенных циклов. Первый вариант вложенного цикла – внутри внешнего цикла последовательно расположено несколько внутренних циклов: for (i=1;i <=n;i++) // внешний цикл < . . . . . . for (j=1;j<=m;j++) // первый внутренний цикл < . . . . . . >// конец первого внутреннего цикла . . . . . . for (k=1;k <=l;k++) // второй внутренний цикл < . . . . . . >// конец второго внутреннего цикла . . . . . . > // конец внешнего цикла Второй вариант организации вложенного цикла – иерархическое расположение циклов (каждый внутренний цикл расположен внутри предыдущего). for (i=1;i <=n;i++) // внешний цикл < . . . . . . for (j=1;j<=m;j++) // первый внутренний цикл < . . . . . . for (k=1;k<=l;k++) // второй внутренний цикл < . . . . . . >// конец второго внутреннего цикла . . . . . . > // конец первого внутреннего цикла . . . . . . > // конец внешнего цикла Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
59 циклов не оказывает влияния на правильность получаемого результата. Например, при вычислении суммы всех элементов матрицы порядок следования циклов может быть произвольным:
| Вариант 1 | Вариант 2 | |
| s=0; | s=0; | |
| for (i=0;i | for | (j=0;j |
| for (j=0;j | for (i=0;i | |
| s+=a[i][j]; | s+=a[i][j]; | |
| Однако при решении многих | задач изменение | порядка вложенности циклов |
приводит к неверному результату. Например, при вычислении суммы элементов каждой строки матрицы изменение порядка расположения циклов приведет к тому, что будут
| вычисляться суммы элементов столбцов. | |
| Вариант 1 (правильный) | Вариант 2 (неправильный) |
| for (i=0;i | for (j=0;j |
| s=0; | s=0; |
| for (j=0;j | for (i=0;i |
| s+=a[i][j]; | s+=a[i][j]; |
| printf ( «S=%7.2f» ,s); | printf ( «S=%7.2f» ,s); |
| > | > |
Необходимость организации вложенных циклов возникает при решении таких широко распространенных задач, как вычисление определенного интеграла с заданной точностью, вычисление экстремума функции на заданном интервале с заданной точностью. Рассмотрим решение этих задач.
5.1.Вычисление определенного интеграла с заданной точностью
Задача вычисления определенного интеграла формулируется следующим образом:
| вычислить I= ∫ b | f ( x ) dx c точностью ε при известных значения пределов интегрирования a, |
| a |
b, известной точностиε и заданной подынтегральной функции f(x). При в ычислении интеграла с точностью будут использоваться изложенные ранее методы прямоугольников, трапеций и парабол для вычисления интеграла при заданном числе разбиений интервала интегрирования. Для оценки погрешности вычисления интеграла на практике используют правило [4]. Суть правила состоит в том, что выполняют вычисление интеграла с двумя разными шагами изменения переменной x, а затем сравнивают результаты вычислений и
Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
60 получают оценку точности. Наиболее часто используемое правило связано с вычислением интеграла дважды: с шагом h и шагом h/2. Для методов прямоугольников и трапеций погрешность R h/2 вычисления интеграла с шагом h/2 оценивается следующей формулой:
| |R h/2 | = | I h / 2 | − I h | , |
| 3 |
где I h/2 – значение интеграла, вычисленное с шагом h/2; I h – значение интеграла, вычисленное с шагом h. Для метода Симпсона погрешность оценивается в соответствии со следующим
| выражением: | ||||
| |R h/2 | | = | I h / 2 | − I h | . |
| 15 | ||||
Шаг интегрирования для методов прямоугольников и трапеций пропорционален величине
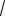ε , поэтому в [2] рекомендовано начальное количество разбиений выбирать согласно следующему выражению n=] b − ε a [ + 1, где ][ — целая часть. Для метода парабол шаг интегрирования пропорционален величине 4 
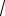ε , поэтому начальное количество шагов рекомендовано выбирать из следующего выражения n=] b 2 4 − ε a [ + 1. В программе вычисления интеграла с точностью во внутреннем цикле находят значение определенного интеграла при заданном (фиксированном) числе разбиений интервала интегрирования.
Во внешнем цикле производится сравнение значений интегралов, вычисленных при числе шагов, равных n и 2n соответственно. Если требуемая точность не достигнута, то производится удвоение числа разбиений, а в качестве предыдущего значения интеграла берется текущее; процесс вычисления интеграла выполняется при новом числе разбиений. В дальнейшем в программах при вычислении значений аргумента используется формула арифметической прогрессии X=X н +(i-1)*dx, а не формула накопления суммы X=X+dx, так как в первом случае получается меньшая погрешность вычислений [5]. b Пример программы вычисления определенного интеграла ∫ xe x dx с точностьюε a методом трапеций ( ( x − 1) e x — первообразная подынтегральной функции). //Вычисление интеграла с точностью. //Метод трапеций. Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
61 #include «stdafx.h» #include #include int _tmain( int argc, _TCHAR* argv[]) < double
| i1 | //предыдущее значение интеграла (число разбиений равно n) |
| ,i2 | //текущее значение интеграла (число разбиений равно 2*n) |
| ,x | //текущее значение аргумента |
| ,xn | //нижний предел интегрирования |
| ,xk | //верхний предел интегрирования |
| ,dx | //шаг изменения аргумента |
| ,s1 | //полусумма значений функции, вычисленных на нижнем и |
| //верхнем пределах интегрирования | |
| ,eps | //точность вычисления интеграла |
| ,itoch; | //точное значение интеграла, вычисленное на основе |
| //первообразной | |
| int | |
| i | //параметр цикла |
| ,n | //количество разбиений интервала интегрирования |
| nn; | //начальное количество разбиений |
printf( «wwedite nach, kon znach, tochnostn» ); scanf( «%lf %lf %lf» ,xk, //ввод исходных данных printf( «Metod trapezijn» ); printf( «Isxodnie dannie xn=%5.2f, xk=%5.2f» ,xn,xk); printf( » eps=%7.1en» ,eps); //вычисление начального количества разбиений nn=(xk-xn)/sqrt(eps)+1; n=nn; dx=(xk-xn)/n; //полусумма значений функции на нижнем и //верхнем пределах интегрирования s1=(xn*exp(xn) + xk*exp(xk))/2.0; //начальное значение интеграла, вычисленное //при начальном количестве разбиений i2=0; for (i=1;i
62 x=xn+i*dx; // текущее значение аргумента //вычисление суммы значений функции в узлах интегрирования i2+=x*exp(x); > //значение интеграла при начальном количестве разбиений i2=(s1+i2)*dx; printf( «Pri nachalnom kolichestve razbienij n=%dn» ,n); printf( «inegral raven %8.4fnn» ,i2); //вложенный цикл вычисления интеграла с точностью do < n*=2; //удвоение количества разбиений i1=i2; //переменной i1присваивается текущее //приближенное значение интеграла dx=(xk-xn)/n; //шаг изменения переменной интегрирования //начальному значению суммы присваивается полусумма //значений функции на концах интервала интегрирования i2=s1; //внутренний цикл для вычисления суммы значений //функции при фиксированном количестве шагов for (i=1;ii2*=dx; //текущее значение интеграла > while (fabs(i2-i1)/3>=eps); //анализ точности вычисления printf( «inegral s tochnostu %7.1e raven %8.4f n» ,eps, i2); printf( «Pri kolichestve razbienij = %dn» ,n); itoch=(xk-1)*exp(xk)-(xn-1)*exp(xn); //точное значение интеграла printf( «nTochnoe znachenie integrala ravno %8.4f» ,itoch); getch(); return 0; > Метод трапеций удобен для вычисления интеграла по правилу Рунге, так как при увеличении количества разбиений в два раза каждый второй узел представляет собой ранее рассматривавшийся узел, поэтому вновь значения функции в этих точках вычислять
Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
63 не следует. Для этого следует сумму значений функции в этих узлах сохранять в переменной s2 . Модифицированная программа приведена ниже. В отличие от первого варианта программы до вложенного цикла необходимо написать цикл вычисления сумм значений функции при начальном разбиении интервала интегрирования для всех узлов, кроме первого и последнего. scanf(«%lf%lf%lf»,xk, n=(xk-xn)/sqrt(eps)+1; s1=(xn*exp(xn) + xk*exp(xk))/2.0; s=0; dx=(xk-xn)/n; //Цикл вычисления суммы значений функции в узлах интегриро- //вания при начальном разбиении интервала интегрирования for (i=1; i i2=dx*(s+s1); s2=s; do < i1=i2; n*=2; dx=(xk-xn)/n; x1=xn+dx; //Координата первого нового узла интегрирования s=0; //Цикл вычисления суммы значений функции //в новых узлах интегрирования for (i=1;i
Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
64 //Сумма значений функции в узлах интегрирования //при новом числе разбиений s2+=s; i2=(s1+s2)*dx; > while (fabs(i2-i1)/3>eps); Полный текст программы приведен ниже: #include «stdafx.h» #include #include int _tmain( int argc, _TCHAR* argv[])
| double i1 | //предыдущее значение интеграла (число разбиений равно n) | |
| ,i2 | //текущее | значение интеграла (число разбиений равно 2*n) |
| ,x | //текущее | значение аргумента |
| ,x1 | // абсцисса первого нового узла интегрирования | |
,xn //нижний предел интегрирования ,xk //верхний предел интегрирования ,dx //шаг изменения аргумента ,s //сумма значений функции, вычисленных в старых узлах //интегрирования ,s1 //полусумма значений функции, вычисленных на нижнем и //верхнем пределах интегрирования ,s2 //сумма значений функции, вычисленных в старых и новых узлах //интегрирования ,eps //точность вычисления интеграла ,itoch; //точное значение интеграла, вычисленное на основе //первообразной int i //параметр цикла ,n //количество разбиений интервала интегрирования ,nn; //начальное количество разбиений printf( «wwedite nach, kon znach, tochnostn» ); //scanf(«%lf %lf %lf»,xk, printf( «Metod trapezijn» ); printf( «Isxodnie dannie xn=%5.2f, xk=%5.2f» ,xn,xk); printf( » eps=%7.1en» ,eps); //вычисление начального количества разбиений n=(xk-xn)/sqrt(eps)+1; s1=(xn*exp(xn) + xk*exp(xk))/2.0; s=0; Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
65 dx=(xk-xn)/n; //Цикл вычисления суммы значений функции в узлах интегриро- //вания при начальном разбиении интервала интегрирования for (i=1; i i2=dx*(s+s1); printf( «ninegral s tochnostu %7.1e raven %8.4f n» ,eps, i2); printf( «Pri nachalnom kolichestve razbienij = %dn» ,n); s2=s; do < i1=i2; n*=2; dx=(xk-xn)/n; x1=xn+dx; //Координата первого нового узла интегрирования s=0; //Цикл вычисления суммы значений функции //в новых узлах интегрирования for (i=1;i//Сумма значений функции в узлах интегрирования //при новом числе разбиений s2+=s; i2=(s1+s2)*dx; > while (fabs(i2-i1)/3>eps); printf( «ninegral s tochnostu %7.1e raven %8.4f n» ,eps, i2); printf( «Pri poslednem kolichestve razbienij = %dn» ,n); itoch=(xk-1)*exp(xk)-(xn-1)*exp(xn); //точное значение интеграла printf( «nTochnoe znachenie integrala ravno %8.4f» ,i2); getch(); return 0; > Оглавление Ю.Е. Алексеев, А.В. Куров «Практикум по программированию на языке C в среде VS C++» Часть 2
Источник: studfile.net
Составление программ с использованием вложенных структур
Необходимость в использовании вложенных циклов возникает достаточно часто. Как правило, она связана с заполнением многомерных таблиц и работой с ними. Продемонстрируем использование вложенных циклов выводом на экран таблицы Пифагора.
Пример 1
Работа этой программы приведет к появлению на экране изображения:
Возможно использование циклов и большей степени вложенности. Однако нужно заметить, что объем вычислений при этом возрастает экспоненциально. Поэтому циклы большой степени вложенности стараются использовать как можно реже.
Источник: oaipbfek.wordpress.com