Часто начинающие программисты задаются вопросом о скорости выполнения кода на разных языках программирования. Это важный вопрос, поскольку выбор языка может значительно повлиять на производительность разрабатываемого программного обеспечения.
Рассмотрим пример. Допустим, у нас есть задача поиска первого треугольного числа, у которого больше 1000 делителей. Это задача может быть решена на нескольких языках программирования, включая C, Python, Erlang и Haskell.
Сравнение скорости выполнения
Когда наши программы, реализованные на разных языках, выполняются, мы видим, что скорость выполнения варьируется от языка к языку. Например, программа на C может выполниться гораздо быстрее, чем аналогичная программа на Python или Haskell. Это объясняется тем, что C — это компилируемый язык, который обычно работает быстрее, чем интерпретируемые языки, такие как Python.
Однако, даже среди интерпретируемых языков могут быть значительные различия в скорости выполнения. Например, программа на Erlang может работать быстрее, чем аналогичная программа на Python, а программа на Python, запущенная с помощью PyPy (альтернативной реализации Python, ориентированной на производительность), может работать быстрее, чем та же программа, запущенная с помощью стандартного интерпретатора Python.
Как найти среднюю скорость движения автомобиля?
Влияние выбора типов данных
Помимо самого языка программирования, выбор типов данных также может повлиять на скорость выполнения кода. В C, например, мы можем использовать тип данных «long» для представления целых чисел. В Python, Erlang и Haskell, с другой стороны, целые числа представляются как числа произвольной длины. Это может замедлить выполнение кода, поскольку работа с числами произвольной длины обычно требует больше вычислительных ресурсов, чем работа с числами фиксированной длины.
Вывод
В заключение, скорость выполнения кода может значительно варьироваться в зависимости от выбранного языка программирования и типов данных. При выборе языка программирования для конкретного проекта важно учесть не только его синтаксис и особенности, но и производительность. Однако помните, что у каждого языка есть свои сильные и слабые стороны, и нет «лучшего» языка для всех задач.
Источник: sky.pro
1.3 Анализ алгоритмов; время работы в лучшем, худшем случаях и в среднем
Рассматривая различные алгоритмы решения одной и той же задачи, полезно проанализировать, сколько вычислительных ресурсов они требуют (время работы, память), и выбрать наиболее эффективный. Конечно, надо договориться о том, какая модель вычислений используется. В данном учебном пособии в качестве модели по большей части используется обычная однопроцессорная машина с произвольным доступом (random-access machine, RAM), не предусматривающая параллельного выполнения операций.
Под временем работы (running time) алгоритма будем подразумевать число элементарных шагов, которые он выполняет. Положим, что одна строка псевдокода требует не более чем фиксированного числа операций (если только это не словесное описание каких-то сложных действий – типа «отсортировать все точки по x-координате»). Следует также различать вызов (call) процедуры (на который уходит фиксированное число операций) и её исполнение (execution), которое может быть долгим.
ОТОРВАЛ трицепс! ЖЕСТЬ!!! Эпичная тренировка с Линдовером
Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности задачи.
Таким образом, будем различать временную T(n) и пространственную V(n) сложности алгоритма. При рассмотрении оценок сложности, будем использовать только временную сложность. Пространственная сложность оценивается аналогично.
Самый простой способ оценки – экспериментальный, то есть запрограммировать алгоритм и выполнить полученную программу на нескольких задачах, оценивая время выполнения программ. Однако, этот способ имеет ряд недостатков. Во-первых, экспериментальное программирование – это, возможно, дорогостоящий процесс. Во-вторых, необходимо учитывать, что на время выполнения программ влияют следующие факторы:
- Временная сложность алгоритма программы;
- Качество скомпилированного кода исполняемой программы;
- Машинные инструкции, используемые для выполнения программы.
Наличие второго и третьего факторов не позволяют применять типовые единицы измерения временной сложности алгоритма (секунды, миллисекунды и т.п.), так как можно получить самые различные оценки для одного и того же алгоритма, если использовать разных программистов (которые программируют алгоритм каждый по-своему), разные компиляторы и разные вычислительные машины. Часто, временная сложность алгоритма зависит от количества входных данных. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики. Существует метод, позволяющий теоретически оценить время выполнения алгоритма, который будет рассмотрен далее. 
Листинг 1.3 – Псевдокод алгоритма сортировки вставками с оценками времени выполнения Для вычисления суммарного времени выполнения процедуры Insertion-Sort отметим около каждой строки её стоимость (число операций) и число раз, которое эта строка исполняется. Для каждого j от 2 до п (здесь п = length[A] – размер массива) требуется подсчитать, сколько раз будет исполнена строка 5, обозначим это число через tj. Строки внутри цикла выполняются на один раз меньше, чем проверка, поскольку последняя проверка выводит из цикла. Строка стоимостью c, повторённая т раз, даёт вклад cm в общее число операций (однако, это выражение нельзя использовать для оценки количества использованной памяти). Сложив вклады всех строк, получим 
Время работы процедуры зависит не только от п но и от того, какой именно массив размера п подан ей на вход. Для процедуры Insertion-Sort наиболее благоприятен случай, когда массив уже отсортирован. Тогда цикл в строке 5 завершается после первой же проверки (поскольку A[i] ≤key при i = j– 1), так что все tj равны 1, и общее время есть 
получаем, что в худшем случае время работы процедуры равно 
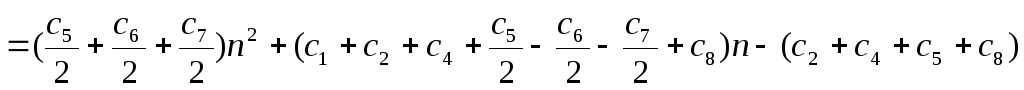В данном случае T(n) – квадратичная (quadratic function), т.е. имеет вид Т(п) = an2+ bn +с. Константы a,b и с здесь также определяются значениями с1. с8. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики. Например, если число тактов (действий), необходимое для работы алгоритма, выражается как 16n2+ 12n log n + 2n + 3, то это алгоритм, для которого T(n) имеет порядок O(n 2 ). При формировании асимптотической O-оценки из всех слагаемых исходного выражения оставляется одно, вносящее наибольший вклад при больших n (остальными слагаемыми можно пренебречь) и игнорируется коэффициент перед ним (так как все асимптотические оценки даются с точностью до константы). Когда используют обозначение O(), имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n 2 ), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов. Таблица 1.2 – Сравнительный анализ скорости роста функций
 |
 |
 |
 |
| 1 | 1 | ||
| 16 | 4 | 64 | 256 |
| 256 | 8 | 2 048 | 65 536 |
| 4 096 | 12 | 49 152 | 16 777 216 |
| 65 536 | 16 | 1 048 565 | 4 294 967 296 |
| 1 048 476 | 20 | 20 969 520 | 1 099 301 922 576 |
| 16 775 616 | 24 | 402 614 784 | 281 421 292 179 456 |
Рисунок 1.1 – Примеры различных функциональных зависимостей Если считать, что числа, приведенные в таблице 1.2, соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму со временем работы T(log n) потребуется 20 микросекунд, а алгоритму со временем работы T(n 2 ) – более 12 дней. Если операция выполняется за фиксированное число шагов, не зависящее от количества данных, то принято писать O(1). Следует обратить внимание, что основание логарифма в асимптотических оценках не пишется. Причина этого весьма проста. Пусть есть O(log2n). Но log2n = log3n / log3 2, а log3 2, как и любую константу, символ О() не учитывает. Таким образом, O(log2n) = O(log3n). К любому основанию можно перейти аналогично, а, значит, и писать его не имеет смысла. Практически время выполнения алгоритма зависит не только от количества входных данных, но и от их значений, например, время работы некоторых алгоритмов сортировки значительно сокращается, если первоначально данные частично упорядочены, тогда как другие методы оказываются нечувствительными к этому свойству. Чтобы учитывать этот факт, полностью сохраняя при этом возможность анализировать алгоритмы независимо от данных, различают:
- максимальную сложность Tmax(n), или сложность наиболее неблагоприятного случая, когда алгоритм работает дольше всего;
- среднюю сложность Tmid(n) – сложность алгоритма в среднем;
- минимальную сложность Tmin(n) – сложность в наиболее благоприятном случае, когда алгоритм справляется быстрее всего.
Теоретическая оценка временной сложности алгоритма осуществляется с использованием следующих базовых принципов:
- Время выполнения операций присваивания, чтения, записи обычно имеют порядок O(1). Исключением являются операторы присваивания, в которых операнды представляют собой массивы или вызовы функций;
- Время выполнения последовательности операций совпадает с наибольшим временем выполнения операции в данной последовательности (правило сумм: если T1(n) имеет порядок O(f(n)), а T2(n) – порядок O(g(n)), то T1(n) + T2(n) имеет порядок O(max(f(n), g(n)));
- Время выполнения конструкции ветвления (if-then-else) состоит из времени вычисления логического выражения (обычно имеет порядок O(1)) и наибольшего из времени, необходимого для выполнения операций, исполняемых при истинном значении логического выражения и при ложном значении логического выражения;
- Время выполнения цикла состоит из времени вычисления условия прекращения цикла (обычно имеет порядок O(1) ) и произведения количества выполненных итераций цикла на наибольшее возможное время выполнения операций тела цикла.
- Время выполнения операции вызова процедур определяется как время выполнения вызываемой процедуры;
- При наличии в алгоритме операции безусловного перехода, необходимо учитывать изменения последовательности операций, осуществляемых с использованием этих операции безусловного перехода.
Итак, время работы в худшем случае и в лучшем случае могут сильно различаться. При анализе алгоритмов наиболее часто используется время работы в худшем случае (worst-caserunningtime), которое определяется как максимальное время работы для входов данного размера. Почему? Вот несколько причин.
- Зная время работы в худшем случае можно гарантировать, что выполнение алгоритма закончится за некоторое время при любом входе данного размера;
- На практике «плохие» входы (для которых время работы близко к максимуму) встречаются наиболее часто. Например, для базы данных плохим запросом может быть поиск отсутствующего элемента (очень распространенная ситуация);
- Время работы в среднем может быть довольно близко к времени работы в худшем случае. Пусть, например, сортируется массив из п случайных чисел с помощью процедуры Insertion-Sort.Сколько раз придётся выполнить цикл в строках 5-8 (листинг 1.3)? В среднем около половины элементов массива A[1..j– 1] больше A[j], так что tj в среднем можно считать равным j/2, и время Т(п) квадратично зависит от n.
В некоторых случаях требуется также среднее время работы (average-caserunningtime,expectedrunningtime) алгоритма на входах данной длины. Конечно, эта величина зависит от выбранного распределения вероятностей, и на практике реальное распределение входов может отличаться от предполагаемого, которое обычно считают равномерным. Иногда можно добиться равномерности распределения, используя датчик случайных чисел.
Источник: studfile.net
Сравнение скорости Python и C++
Прим. ред. Это перевод статьи Назера Тамими. Мнение редакции может не совпадать с мнением автора оригинала.
Есть миллион причин любить Python (особенно если вы дата-сайентист). Но насколько Python отличается от низкоуровневых языков, таких как Си и C++? В этой статье я собираюсь сделать сравнение скорости Python и C++, на очень простом примере.