Если Вы хоть немного знакомы с теорией графов, Вам наверняка интересно, как же правильно хранить граф в памяти компьютера. В этой статье рассмотрено 4 способа, как это сделать. Также проведён полный их анализ и размышления на эту тему.
- Введение
- Матрица смежности
- Описание Бержа
- Список дуг
- Список смежности
- Оптимизация к списку смежности
- Заключение
Введение
Для начала разберёмся, что же такое граф и какие они бывают.
Граф — множество V вершин и набор E неупорядоченных и упорядоченных пар вершин. Говоря проще, граф — это множество точек (вершин) и соединяющих их путей (дуг или рёбер). Граф может быть ориентированным и неориентированным. В ориентированном графе пути (дуги) имеют направление, а в неориентированном — не имеют. Пути в неориентированном графе называются рёбрами.
Взвешенным называется такой граф, для каждого ребра(дуги) которого определена некоторая функция. А эта функция называется весовой.
Хранение графов (часть 1) — три базовых метода. Очень просто и с примерами.
Рассмотрим пример ориентированного взвешенного графа:
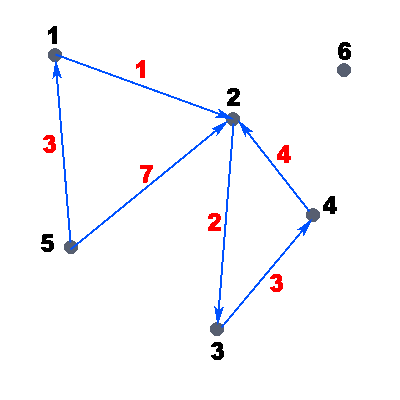
На рисунке точками обозначены вершины графа, стрелками — дуги, чёрные числа — номера вершин графа, а красные — веса дуг. Вес дуги можно представить также как стоимость. Т.е. например: дан граф, нужно дойти от вершины i до вершины j, заплатив минимальное количество денег/потратив наименьшее количество времени. Пусть в нашем графе, который представлен на рисунке, нам нужно пройти из вершины 5 в вершину 2, а вес дуг — стоимость прохода по данному ребру. В данном примере очевидно, что выгоднее пройти через вершину 1 и только потом прийти в вершину 2, так мы заплатим всего 4 единицы денег, иначе, если пойти напрямую, мы заплатим целых 7 единиц.
Ну вот мы и разобрались, что такое граф. На рисунке всё смотрится красиво, все задачи вроде бы решаются легко… Но! А если граф будет действительно большим, например на 1000 вершин? Да, такой граф на бумажке рисовать очень долго и неприятно… Пускай лучше всё это делает за нас компьютер!
Теперь осталось только научить компьютер работать с графами. Сам я довольно часто участвую в олимпиадах по информатике, а там очень любят давать задачи на графы. От того, как хранить граф в той или иной задаче очень много зависит… После того, как я придумал полное решение, но, написав его, получил только половину баллов, я задумался, а правильно ли я хранил граф?
Проблема правильного хранения графа в памяти компьютера действительно актуальна в сегодняшние дни. Я решил выяснить, так какой же из способов всё-таки лучше.
Матрица смежности
Я намеренно употреблял слово “дуга”, т.к. матрица смежности приспособлена ТОЛЬКО для ориентированных графов. Очень много способов хранения приспособлены только для ориентированных графов. Однако почти во всех задачах ребро можно заменить двумя дугами, т.е. если у нас есть ребро (1,3), то мы можем заменить его на дуги (1,3) и (3,1) — так мы сможем пройти в любом направлении в любое время.
Информатика. Теория графов: Способы хранения графа. Центр онлайн-обучения «Фоксфорд»
Как вы уже заметили, в матрице смежности нам часто нужно хранить большое количество нулей. Например, в нашей матрице “нужных” значений только 6, а остальные 30 — нули, не представляющие для нас почти никакой нужной информации.
Для представления графа матрицей смежности нужно V в квадрате (где V — количество вершин). Если граф почти полный, т.е. Е почти развно V в квадрате (где Е — количество дуг), этот способ хранения графа наиболее выгоден, т.к. его очень просто реализовывать и память будет заполнена “нужными” значениями.
Кроме большого количества требуемой памяти и медленной работы на разреженных графах у матрицы смежности есть ещё один важный недостаток. Иногда в задачах нужно выводить не номера вершин, а номера дуг(рёбер) на вводе. Хранить эти номера матрица смежности не умеет. Нужно реализовывать восстановление номера дуги(ребра) как-то иначе, а это совсем неудобно.
Описание Бержа
В нулевом столбце хранятся “длины” строк. Однако, вес дуг никак не хранится, а если его хранить отдельно, то нужно заводить ещё один массив размером V в квадрате…
Список дуг
Графы. Способы представления графа в программе
В качестве простейшего примера графа часто приводят систему дорог между городами, где города — это вершины, а дороги — ребра графа. Однако, вокруг нас есть множество и более обыденных примеров:

- электрическая схема является графом, в котором вершины — элементы схемы, а дуги — соединяющие провода;
- блок-схема алгоритма;
- система каталогов операционной системы является частным случаем графа — каталоги и папки задаются вершинами, а отношение вложенности — дугами.
Если направление ребер графа имеет значение (например при отражение отношения вложенности каталогов) — то граф называется ориентированным. Если направление не важно (например при соединении элементов электрической цепи) — граф является неориентированным. Кроме того, ребрам часто приписывается вес, граф в этом случае называется взвешенным — в системе дорог веса ребер могут отражать расстояния между городами.
В связи с этим возникает необходимость обработки графов компьютером, но для этого необходимо сначала каким-то удобным для обработки образом разместить его в памяти. Итак, граф ( G ) — это совокупность вершин ( V ), и дуг ( E ), в зависимости от того, как они задаются, выделяются следующие способы машинного представления графа:
- матрица смежности для графа из N вершин хранится в виду двумерного массива размером N x N . Вершины графа в этом случае задаются номерами (индексами строк и столбцов матрицы), а ячейка графа matrix[i, j] отражает наличие дуги между соответствующими вершинами. Например, при наличии дуги в ячейке может быть записана единица (или вес ребра i->j для взвешенного графа) , а при отсутствии — ноль;
- матрица инцидентности для графа из N вершин и M дуг хранится в виде двумерного массива размером N x M . Ячейка матрицы matrix[i, j] отражает инцидентность ребра j вершине i , т.е. тот факт, что это ребро выходит или входит в вершину i . Если ребро не связано с вершиной — в соответствующей ячейке матрицы записывается ноль, в противном случае единица (если граф ориентированный, то начало ребра можно отметить -1 , а конец 1 , если граф взвешенный — единица может быть заменена весом соответствующего ребра).

Матрица смежности графа:
| A | B | C | D | E | F | G | |
| A | 12 | 16 | 3 | ||||
| B | 12 | 8 | 6 | ||||
| C | 8 | 4 | 8 | ||||
| D | 4 | 14 | 30 | ||||
| E | 14 | 28 | 11 | ||||
| F | 16 | 28 | 13 | ||||
| G | 3 | 6 | 8 | 30 | 11 | 13 |
Матрица инцидентности графа:
| AB | BC | CD | DE | EF | FA | AG | BG | CG | DG | EG | FG | |
| A | 12 | 3 | ||||||||||
| B | 12 | 8 | 6 | |||||||||
| C | 8 | 4 | 8 | |||||||||
| D | 4 | 14 | 30 | |||||||||
| E | 14 | 28 | 11 | |||||||||
| F | 28 | 16 | 13 | |||||||||
| G | 16 | 3 | 6 | 8 | 30 | 11 | 13 |
Работая с приведенными матрицами возможно, например, найти в графе кратчайшие пути между вершинами, построить минимальные остовы и т.д., однако, у них есть недостатки:
- избыточность. Зачастую в графах ребра существуют между небольшим (количеством вершин), поэтому в матрице смежности будет огромное количество нулей. В матрице инцидентности в каждом столбце может быть лишь два ненулевых значения (т.к. у дуги два конца). На хранение нулей тратится память, что может быть существенно при обработки больших графов;
- недостаточная расширяемость. В матрицу смежности можно без проблем добавлять новые дуги, но чтобы добавить вершину нужно создавать новую матрицу большего размера и копировать в нее данные из старой. Это работает очень медленно при больших матрицах. В матрице инцидентности такие проблемы возникнут как при добавлении дуг, так и при добавлении вершин.
В связи с этим, зачастую применяются списки смежности и инцидентности. Для каждой вершины при этом хранится список с номерами смежных вершин или инцидентных ребер. В качестве структуры данных при этом могут использоваться массивы, связные списки и даже хеш-массивы.
Списки смежности графа:
| A | B(12) | F(16) | G(3) | |||
| B | A(12) | C(8) | G(6) | |||
| C | B(8) | D(4) | G(8) | |||
| D | C(4) | E(14) | G(30) | |||
| E | D(14) | F(28) | G(11) | |||
| F | A(16) | E(28) | G(13) | |||
| G | A(3) | B(6) | C(8) | D(30) | E(11) | F(13) |
Списки смежности и инцидентности решают проблему расширяемости графа, т.к. новые узлы и дуги могут быть очень просто и эффективно добавлены во время выполнения программы, кроме того они более оптимальны по памяти, т.к. хранятся только данные о существующих дугах. Однако, такой способ представления графа менее эффективен по процессорному времени, т.к. для проверки существования дуги в худшем случае нужно будет перебрать все дуги, выходящие из некоторой вершины, но в матрице смежности было достаточно обратиться к элементу массива (асимптотическая сложность ухудшилась с O(1) до O(K) при использовании связных списков или O(log(K)) при использовании хеш-массивов). Важно, что K в этом случае — количество смежных вершин, для многих графов оно не будет очень большим (например, если граф представлял бы карту города, то скорее всего значение K для каждой вершины не превышало бы 4-6 ), в связи с этим, нужно очень внимательно выбирать структуру данных для хранения списков смежности/инцидентности.
Еще одним способом задания графа в программе может быть хранение указателей на смежные вершины/инцидентные дуги внутри каждого узла программы, при этом узел описывается в виде структуры, содержащей данные и эти указатели. Примерно так:
struct Node < int value; std::listadj; >
Сам граф в программе хранится в виде списка таких вершин.
Литература по теме:
- Анализ сложности алгоритмов. Примеры — поможет разобраться с оценкой сложности по памяти и процессорному времени (нужно чтобы уметь выбирать наиболее подходящую для своей задачи структуру данных);
- Макоха А. Н., Сахнюк П. А., Червяков Н. И. Дискретная математика: Учеб. пособие. — М. ФИЗМАТЛИТ, 2005 — 368 с.
- Дж. Макконелл Анализ алгоритмов. Активный обучающий подход. — 3-е дополненное издание. М: Техносфера, 2009. -416с.
Источник: pro-prof.com
Способы хранения графа в памяти компьютера

В предыдущей статье мы познакомились с терминами и определениями теории графов. В этой же статье обсудим различные способы представления графа в памяти компьютера для его обработки. Покажем, какие структуры данных можно использовать, а также проговорим преимущества и недостатки каждого способа.

Допустим, у нас есть неориентированный граф G из V = 5 вершин и E = 6 рёбер. Вершины пронумерованы от 1 до 5, рёбра для удобства также пронумеруем буквами a, b, c, d, e. Одна вершина с петлёй, изолирована от других.
Перечисление множеств
По определению, граф — это топологическая модель, которая состоит из множества вершин и множества рёбер, их соединяющих. Значит, самый “простой” способ представить граф — определить оба этих множества.

Лично мне ни разу не доводилось видеть алгоритм обработки графа, который бы использовал такой способ хранения вершин и рёбер.
Недостаток такого подхода: использование достаточно тяжеловесной структуры – хэш таблицы – для хранения множества, когда проще и быстрее работать с обычными массивами или списками, к тому же, во множестве нет возможности получить перечисление вершин в порядке их добавления (особенность хэш-таблицы).
Кстати, сами вершины обычно вообще отдельно не хранятся, а указывается только их количество V, они автоматически принимают номера от 0 до V-1. Для хранения цвета / веса или других характеристик вершин можно использовать параллельные массивы для каждого критерия.
Матрица смежности
Это самый популярный и расточительный способ представления графа в памяти. Его уместно использовать, если количество рёбер велико, порядка V 2 .
Для хранения рёбер используется двумерная матрица размерности [V, V], каждый [a, b] элемент которой равен 1, если вершины a и b являются смежными и 0 в противном случае.
В случае неориентированного графа матрица является симметричной относительно главной диагонали, а сумма каждой строчки и каждого столбца равна степени вершины. В связи с этим, при записи рёбер-петель в матрицу необходимо записывать число 2.

Сложность по памяти: O(V 2 ).
Сложность перечисления всех рёбер: O(V 2 ).
Сложность перечисления всех вершин, смежных с а: O(V).
Сложность проверки смежности вершин a и b: О(1).
Матрица инцидентности
Это самый расточительный способ хранения графа, его уместно использовать, если количество рёбер невелико.
Для хранения используется двумерная матрица размера [V, E], в каждом столбце которой записано одно ребро таким образом: напротив вершин, инцидентных этому ребру, записаны 1, в остальных случаях 0.
Таким образом, сумма чисел в каждом столбце равна 2, а сумма чисел в строчке a равна степени вершины а.

Сложность по памяти: O(V x E).
Сложность перечисления всех рёбер: O(V x E) — хоть каждое ребро и хранится в отдельном столбце, но для получения информации об инцидентных ему вершинах нужно перебрать все числа в столбце.
Сложность перечисления всех вершин, смежных с а: O(V x E).
Сложность проверки смежности вершин a и b: O(E) — достаточно пройтись по строчкам a и b в поисках двух единиц.
Перечень рёбер
Если из матрицы инцидентности убрать все нули, в каждом столбце останется только два числа для каждого ребра — номера инцидентных ему вершин. То есть, для перечисления рёбер достаточно составить список из пар чисел, это очень экономный способ: каждое ребро хранится один раз, когда во всех других вариантах каждое ребро, как правило, записывается дважды.
Недостаток — при поиске вершин в списке рёбер нужно выполнять по две проверки — сравнивать и первую вершину, и вторую.

Сложность по памяти: O(E).
Сложность перечисления всех рёбер: O(E).
Сложность перечисления всех вершин, смежных с а: O(E).
Сложность проверки смежности вершин a и b: О(E).
Список рёбер можно сгруппировать по вершинам, что позволит ускорить поиск смежных вершин. У нас получится ещё три очередных способа, которые очень похожи друг на друга, отличаются лишь способом записи векторов.
Векторы смежности
Для записи вектора смежности используется двумерная матрица размером [V, S], где S — максимальная степень вершины в графе.
В каждой строчке a записаны номера вершин, смежных с а, после чего записаны нули (несуществующие номера вершин).

Сложность по памяти: O(V x S).
Сложность перечисления всех рёбер: O(V x E)
Сложность перечисления всех вершин, смежных с а: O(Sa) (Sa = степень вершины а) = O(E)
Сложность проверки смежности вершин a и b: О(Sa) = O(Sb) = O(E)
Массивы смежности
Для экономии памяти, используется ступенчатый массив, длина каждой строки равна степени данной вершины.
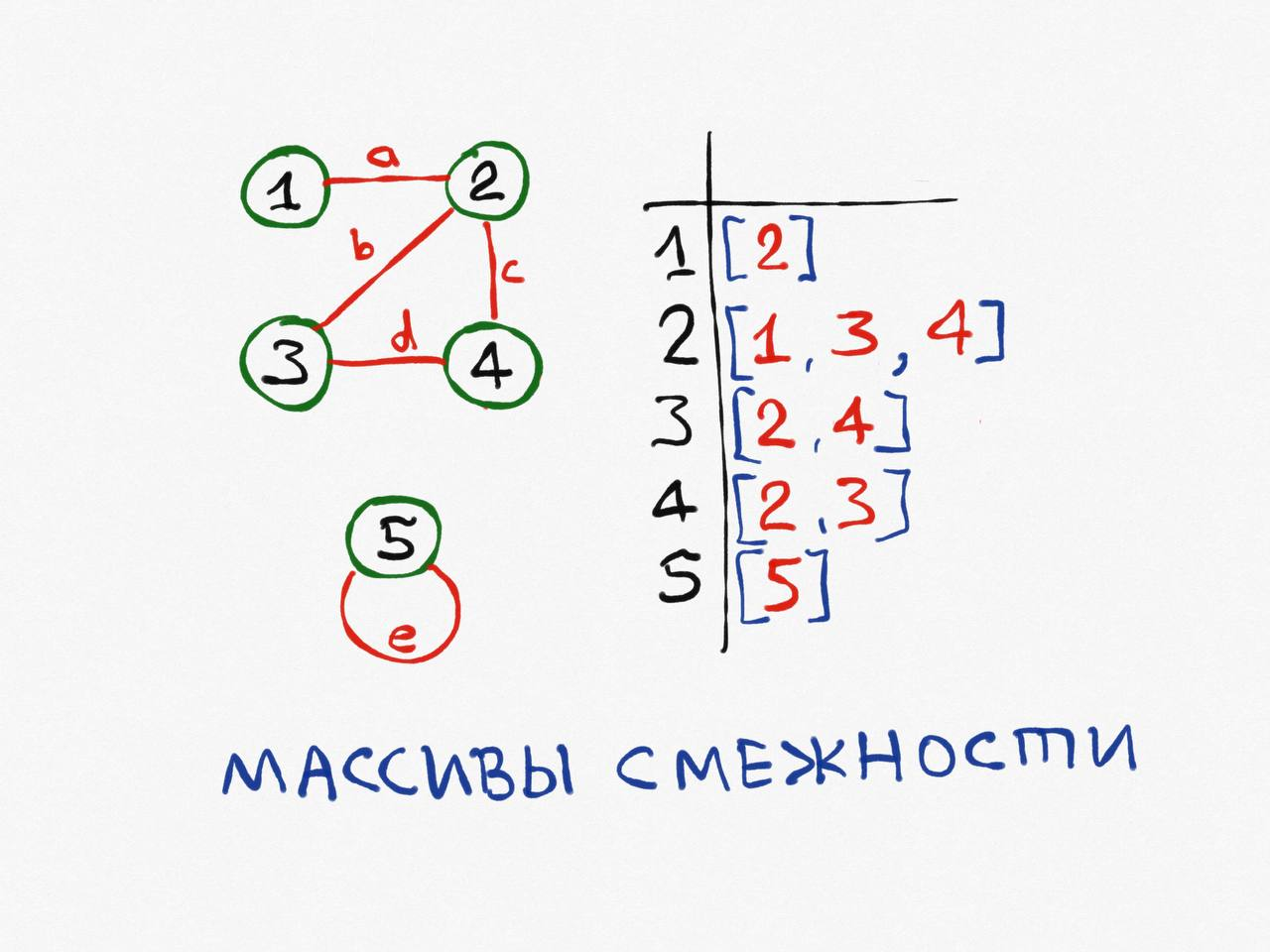
Сложность по памяти: O(сумма степеней всех вершин) = O(E).
Списки смежности
Здесь используется односвязный список для перечисления всех смежных вершин.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + 2xE) = O(V + E)
Структура с оглавлением
Один из самых экономных способов представления графа в памяти. Фактически, мы записываем все массивы смежности в одну строчку, в один линейный массив, и создаём массив-оглавление, с указателями на начало списка для каждой вершины.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + E).
Список вершин и список рёбер
Самый экстравагантный способ хранения графа.
Вершины записываются в односвязных список, от каждой вершины есть указатель на список всех рёбер, инцидентных данной вершины. Каждое ребро, в свою очередь, имеет указатель на вторую инцидентную ей вершину и на следующее ребро.

Получается весьма разветвлённый граф для представления графа.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + E).
Сложность перечисления всех рёбер: O(V x E)
Сложность перечисления всех вершин, смежных с а: O(Sa) (Sa = степень вершины а) = O(E)
Сложность проверки смежности вершин a и b: О(Sa) = O(Sb) = O(E)
Теперь, когда мы знаем способы представления графа в памяти компьютера, можем выбирать наиболее приемлемые варианты для каждой конкретной задачи.
На курсе «Алгоритмы и структуры данных» мы рассматриваем следующие алгоритмы в модуле “Теория графов”: поиск вширь и вглубь, топологическая сортировка (Кана, Таряна, Демукрона), поиск компонент сильной связности (Косарайю), поиск минимального скелета (Прима, Краскала, Борувки), поиск кратчайшего пути (Флойда-Уоршалла, Баллмана-Форда, Дейкстры), алгоритм Джонсона для поиск кратчайшего пути в орграфе с отрицательными дугами (см. мою статью), решение задачи коммивояжера (ближайшего соседа, кратчайшего ребра, ближайшего посредника) и вишенка на торте — алгоритм А* звезда поиска кратчайшего пути с эвристической функцией.
Также хочу пригласить всех желающих на бесплатный демоурок по теме «Дерево отрезков — быстро и просто». Зарегистрироваться на урок.
- Блог компании OTUS
- Алгоритмы
Источник: habr.com