Применим форму , чтобы найти переменные, используемые для вычисления амплитуды, периода, сдвига фазы и смещения по вертикали.
Найдем амплитуду .
Найдем период .
Нажмите для увеличения количества этапов.
Период функции можно вычислить по формуле .
Заменим на в формуле периода.
Абсолютное значение ― это расстояние между числом и нулем. Расстояние между и равно .
Разделим на .
Найдем сдвиг фазы, используя формулу .
Нажмите для увеличения количества этапов.
Сдвиг фазы функции можно вычислить по формуле .
Сдвиг фазы:
Заменим величины и в уравнении на сдвиг фазы.
Сдвиг фазы:
Разделим на .
Сдвиг фазы:
Сдвиг фазы:
Перечислим свойства тригонометрической функции.
Сдвиг фазы: нет
Смещение по вертикали: нет
Выберем несколько точек для построения графика.
Нажмите для увеличения количества этапов.
Найдем точку в .
Нажмите для увеличения количества этапов.
Заменим в этом выражении переменную на .
Построение графика функции y=cos(x-пи/4)
Упростим результат.
Нажмите для увеличения количества этапов.
Точное значение : .
Окончательный ответ: .
Найдем точку в .
Нажмите для увеличения количества этапов.
Заменим в этом выражении переменную на .
Упростим результат.
Нажмите для увеличения количества этапов.
Точное значение : .
Окончательный ответ: .
Найдем точку в .
Нажмите для увеличения количества этапов.
Заменим в этом выражении переменную на .
Упростим результат.
Нажмите для увеличения количества этапов.
Применим угол приведения, найдя угол с эквивалентными тригонометрическими значениями в первом квадранте. Добавим минус к выражению, так как косинус отрицательный во втором квадранте.
Источник: www.mathway.com
Построение графика
Решение этой задачи удобно проводить в следующем порядке:
- Определим границы значений аргумента в декартовых координатах, в пределах которых будет строиться график X
[Xmin, Xmax]. - Для данной области значений аргумента определим предельные значения функции: Y
[Ymin, Ymax]. Эти значения необязательно должны быть точными. Они могут быть оценочными снизу и сверху соответственно. - Зададим границы графического окна в графических координатах, в пределах которого будет рисоваться график: [Xgmin, Xgmax] – по горизонтали, [Ygmin, Ygmax] – по вертикали.
- Учесть, что Ygmin > Ygmax, поскольку в графических координатах вертикальная ось направлена вниз.
Таким образом, имеем две системы координат [x, y] – математическая или декартова система координат и [xg, yg] – экранная система координат. Получим формулы связи между этими системами. Нетрудно получить формулу, связывающую экранные и математические координаты: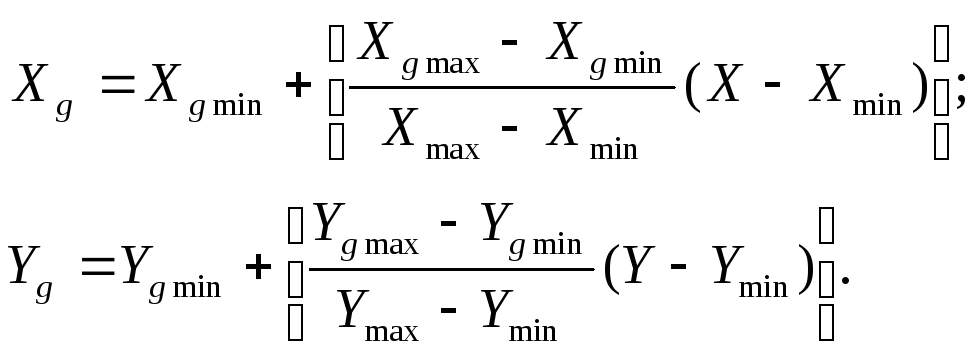 
(*) Здесь квадратные скобки означают округление до целого значения (функция Round). Построение графика функции может производиться либо точечным методом, либо кусочно-линейным. При первом способе график строится как последовательность точек, расположенных максимально близко. Производится «попикселевый» перебор значений аргумента xg в интервале [Xgmin,Xgmax] с выставлением точек с соответствующими координатами Yg. При кусочно-линейном методе задается шаг ΔX и рассчитывается последовательность значений (Xi,Yi):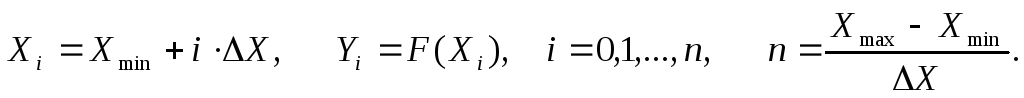
10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графики
Точечный метод построения графика
Составим программу построения графика функции у = cos(x) для х
[0; 2π], используя точечный метод. Из условия задачи следует, что Xmin = 0, Хтax= 2π.
В этих пределах функция cos х меняется от -1 до 1. Поэтому Ymin = -1, Ymax = 1. Выберем следующие границы графического окна: Xgmin=10; Xgmax=400; Ygmin= 300; Ygmax=40.
График строится в виде последовательности точек с математическими координатами Xi = Xmin + i ∙ h; Yi =cos(Xi); i = 0, . 390. Шаг h выбирается минимально возможным, соответствующим шагу графической сетки: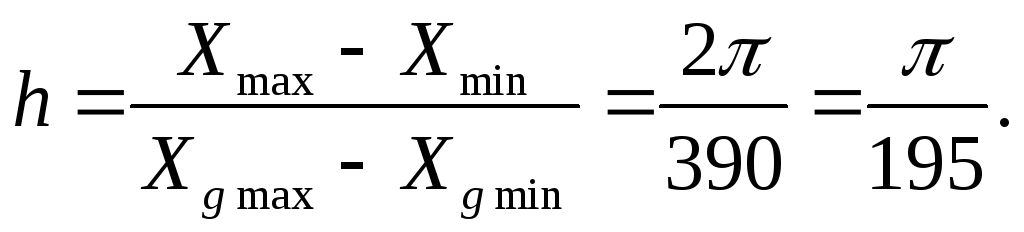 
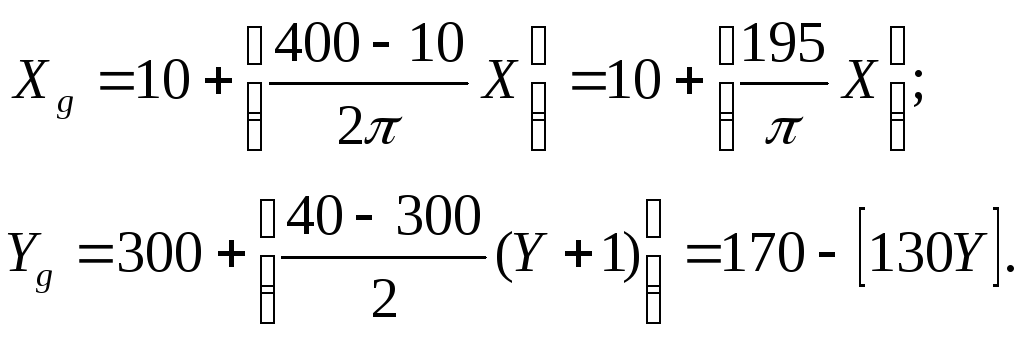Вместе с графиком функции строятся оси координат. Строить их будем с помощью команды рисования линии line. Ось X имеет координату Yg= 170, ось Y — координату Xg = 10. Uses Graph; Var Driver,Mode: Integer; X: Real; Xg,Yg,I: Integer; Begin Driver:=Detect; InitGraph(Driver,Mode,’C:TPBGI’); SetColor(White); SetBkColor(DarcGray); Line(10,170,400,170); Line(10,20,10,320); x:=0; For I:=0 To 390 Do Begin Xg:=10+Round(195/(Pi)*(X)); Yg:=170-Round(130*cos(X)); PutPixel(Xg,Yg,Yellow); X:=X+Pi/195 End; OutTextXY(15,30,’Y’); OutTextXY(405,170,’X’); OutTextXY(190,40,’Y=COS(X)’); ReadLn; CloseGraph; End. 
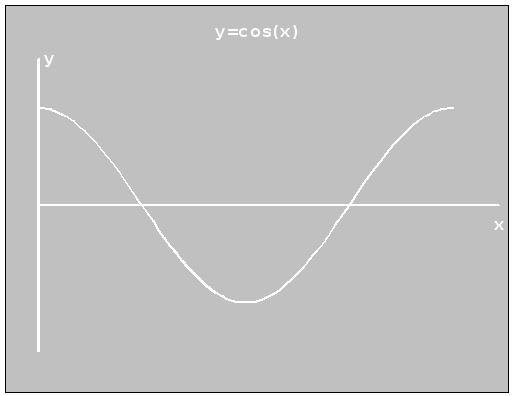Рисунок 1
Источник: studfile.net
Пример написания программы. Задание: составить программу, отображающую графики функций sin(x) и cos(x) на интервале [Xmin, Xmax]
Задание: составить программу, отображающую графики функций sin(x) и cos(x) на интервале [Xmin, Xmax]. Предусмотреть возможность изменения разметки координатных осей, а также шага построения таблицы.
Прежде всего, следует определить в коде класса все необходимые переменные и константы. Конечно, можно обойтись и без этого, вставляя значения в виде чисел прямо в формулы, но это, во-первых, снизит читабельность кода программы, а во вторых, значительно усложнит изменение каких-либо параметров программы, например, интервала построения графика.
/// Левая граница графика
private double XMin = -Math.PI;
/// Правая граница графика
private double XMax = Math.PI;
private double Step = (Math.PI * 2) / 10;
// Массив значений X — общий для обоих графиков
private double[] x;
// Два массива Y — по одному для каждого графика
private double[] y1;
private double[] y2;
Также в коде класса следует описать глобальную переменную типа Chart, к которой мы будем обращаться из разных методов:
Поскольку данный класс не входит в пространства имен, подключаемые по умолчанию, следует выполнить дополнительные действия. Во-первых, в Обозревателе решений нужно щёлкнуть правой кнопкой по секции Ссылки и добавить ссылку на библиотеку визуализации (рис. 8.2):
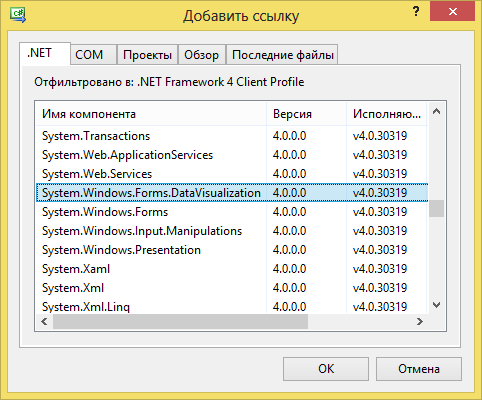
Рис. 8.2. Добавление ссылки на библиотеку визуализации.
Кроме того, следует подключить соответствующее пространство имен:
Далее следует определить метод, который будет расчитывать количество шагов и вычислять значения функций в каждой точке, внося вычисленные значения в массивы x, y1 и y2:
/// Расчёт значений графика
private void CalcFunction()
// Количество точек графика
int count = (int)Math.Ceiling((XMax — XMin) / Step)
// Создаём массивы нужных размеров
x = new double[count];
y1 = new double[count];
y2 = new double[count];
// Расчитываем точки для графиков функции
// Вычисляем значение X
x[i] = XMin + Step * i;
// Вычисляем значение функций в точке X
После расчёта значений нужно отобразить графики на форме с помощью элемента Chart. Элемент управления Chart нельзя выбрать с помощью панели элементов – его нужно создавать прямо в коде программы. Вторым шагом следует созать область отображения графика и настроить внешний вид осей:
/// Создаём элемент управления Chart и настраиваем его
private void CreateChart()
// Создаём новый элемент управления Chart
chart = new Chart();
// Помещаем его на форму
// Задаём размеры элемента
chart.SetBounds(10, 10, ClientSize.Width — 20,
// Создаём новую область для построения графика
ChartArea area = new ChartArea();
// Даём ей имя (чтобы потом добавлять графики)
// Задаём левую и правую границы оси X
// Определяем шаг сетки
// Добавляем область в диаграмму
// Создаём объект для первого графика
Series series1 = new Series();
// Ссылаемся на область для построения графика
// Задаём тип графика — сплайны
// Указываем ширину линии графика
// Название графика для отображения в легенде
// Добавляем в список графиков диаграммы
// Аналогичные действия для второго графика
Series series2 = new Series();
// Создаём легенду, которая будет показывать названия
Legend legend = new Legend();
Наконец, все эти методы следует откуда-то вызвать. Чтобы графики появлялись сразу после запуска программы, надо вызывать их в обработчике события Load формы:
private void Form1_Load(object sender, EventArgs e)
// Создаём элемент управления
// Расчитываем значения точек графиков функций
// Добавляем вычисленные значения в графики
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru