Составьте программу для вычисления значения функции в точке x

Содержание

Составить программы для вычисления в произвольной точке x значений функций , определяемых следующими графиками:
Параметры a, b, c, берутся из таблицы 1.

Таблица №1
a 0,267
b 0,173
c 0,098

#pragma hdrstop #include #include #define a 0.267 #define b 0.173 #define c 0.098 namespace < float kb(float y, float x) < if (x >pow(y, 2)) return 0.8; if (x == pow(y, 2)) return x*(-1); else return 0.13*x; >; >; int main() < float f, x, y; y = a/b — c; std::cout

Все равно что-то не так в задачнике как бы есть пример, вот такой немного по другому выходит

#include void main() < double f, x, y, absy; printf(«n введите x = «); scanf(«%lf», y = x * x — 1.; if (y < 0) absy = -y; /* вычисление | y | */ else absy = y; if (absy printf(«n f = %f», f); >
Изображения

Снимок экрана 2011-02-14 в 12.36.28.png (18.6 Кб, 57 просмотров)

Источник: www.programmersforum.ru

Вычисление значений функций по формуле. Алгебра, 7 класс

Решение уравнений методом касательных (алгоритм Ньютона) на C#

Функция (Метод касательных)

Привет! Сегодня посмотрим, как приближённо решать уравнения с помощью метода касательных (алгоритма Ньютона).
И напишем программу на языке программирования C#.
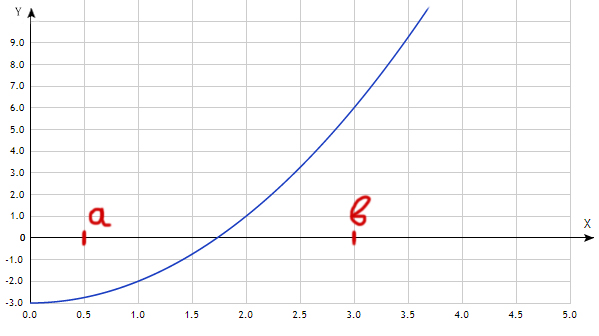
Пусть дано нелинейное уравнение: f(x) = 0 (Если уравнение будет линейное, то невозможно будет провести касательную). Метод касательных поможет приближённо найти корень уравнения на отрезке [a, b], при условии, что функция непрерывна на замкнутом интервале [a, b], и корень на этом отрезке только один! А так же функция не меняет свою вогнутость или выпуклость (постоянный знак второй производной) и не имеет экстремумов (первая производная не равна нулю) на отрезке [a, b].
Графически функция может выглядеть следующим образом:

Читайте также:

Чит программа на русском

Т.е. самая стандартная функция.

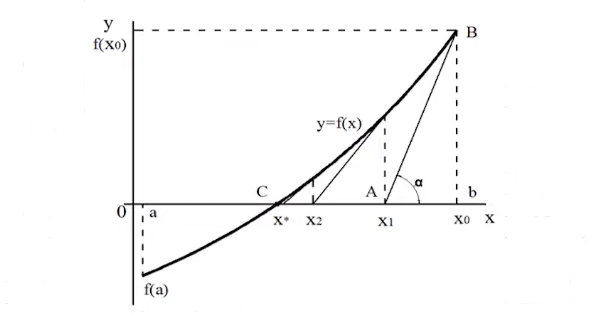
Графическая интерпретация метода Ньютона

Графическая интерпретация метода Ньютона:

От x0 узнаём значение функции. В этой точке проводим касательную. Касательная пересекает ось X, и мы получаем новую точку x1. И начинаем всё сначала. Числа x0, x1, x2 и т.д. приближаются к корню уравнения.
Выведем формулу для xn.

Уравнение касательной:
y = f(x0) + f′(x0)(x-x0)

Приравняем к нулю (пересечение с осью X) и выразим x.
x1=x0 — f(x0) / f′(x0)
xn+1=xn — f(xn) / f′(xn)

x0 = a, если f(a)*f′′(x)>0
x0 = b, если f(b)*f′′(x)>0

Для примера, найдём положительный корень уравнения: x 2 = 2

Определим отрезок [1, 2], где будем искать корень.

Функция f(x) = x 2 — 2

f′′(x) = 2
f(2) = 4 — 2 = 2

Значит, x0 = 2, т.к. f′′(x) * f(2) > 0.

Определим корень уравнения с точностью до ε=0.001 на языке программирования C#.

using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ConsoleApp64 < class Program < static void Main(string[] args) < double x0, xn, xnp1, e; e = 0.001; x0 = 2; xn = x0 — (Math.Pow(x0, 2)-2)/(2*x0) ; xnp1 = xn — (Math.Pow(xn, 2)-2)/(2*xn); while (xn — xnp1 >= e) < xn = xnp1; xnp1 = xn — (Math.Pow(xn, 2)-2) / (2 * xn); > Console.WriteLine(«», xnp1); > > >

Т.к. x0 — не участвует при вычислении погрешности, то мы в начале до цикла while вычисляем xn и xn+1 (xnp1). Т.к. тип данных double, то чтобы возвести число в степень, используем специальную функцию Math.Pow(). В условии цикла while мы используем разницу без модуля, потому что мы идём от правого конца отрезка, и xn всегда больше, чем xnp1.

Метод Ньютона - программа на Си шарп

Источник: code-enjoy.ru