Решение: внешний алфавит машины будет следующим: , 0, 1>.
Будем считать начальной следующую конфигурацию: q11…p. Для того, чтобы прибавить 1 к двоичному числу n сначала необходимо «отогнать» головку машины вправо и установить ее под последней (самой младшей) цифрой двоичного числа. Если последняя цифра числа есть 0, то достаточно заменить 0 на 1 и завершить процесс, то есть перевести головку (машину) в заключительное состояние q0.
Если же последняя цифра числа есть 1, то необходимо заменить ее на 0, а головку сдвинуть влево, чтобы «увидеть» следующий разряд двоичного числа. Если окажется, что этот разряд содержит 0, то заменить 0 на 1 и опять-таки перевести головку (машину) в заключительное состояние q0. Если же этот разряд содержит 1, необходимо заменить ее на 0 и опять сдвинуть головку влево. И так далее, до тех пор, пока либо не встретится разряд, содержащий 0, либо головка дойдет до первого слева пустого символа . В любом из этих случаев 0 или следует заменить на 1 и перевести головку (машину) в заключительное состояние q0.
Как запрограммировать на машине Тьюринга сложение? Душкин объяснит
Программа машины, прибавляющей 1 к двоичному числу, имеет вид:
q11 q11R
q10 q10R
q1 q2L
q20 q31H
q21 q20L
q2 q01H
q31 q31L
q30 q30L
q3 q0R.
2. Пусть требуется перевести запись натурального числа n, изображенного в виде последовательности n «палочек» (|) n 1, в двоичную запись в алфавите . Т.е. конфигурация q1|||…| должна быть преобразована в q012…p , где 12…p — двоичная запись n.
Решение: в качестве внешнего алфавита машины берем алфавит:, |, 0,1>.
Опишем алгоритм решения задачи в словесной форме:
Источник: studfile.net
Универсальная Машина Тьюринга
Для решения данной задачи нам необходимо определить множество всех значений алфавита, так как речь идет о двоичной системе счисления, то в поле “ алфавит ” запишем числа 0 и 1. Программа автоматически добавит в столбец слева от таблицы «программа» введенные числа и знак пустой ячейки — ]. В задаче не сказано, к какому именно числу необходимо добавить единицу, а значит, берем произвольное двоичное число и записываем его в поле «слово».
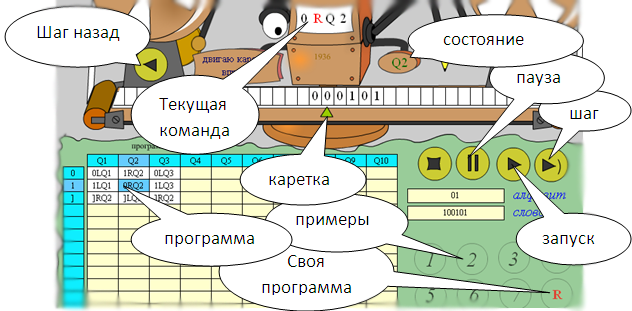
Далее самое интересное – кодирование. Из условия задачи для пункта «а» сказано, что каретка находится слева от слова, это значит что само слово нужно еще и найти. Сам автомат (каретка) кроме текущей ячейки ничего не видет, он может только прочитать ее содержимое и на основании значения, которое он считывает, безусловно выполняет поручения. А видит он пустую ячейку. Даем команду двигать в право до тех пор, пока он не увидит начало слова — команда ]RQ1. С точки зрения автомата:
если ячейка пуста
- нахожусь в состоянии Q1
- считываю значения текущей ячейки
- если она пуста то записываю в нее пустоту (звучит странно но так оно и есть, хотя я всеже добавил здравый смысл в свой эмулятор и он просто пропускает такой шаг)
- двигаю каретку вправо на один шаг
- перехожу (даже если я и находился там) в состояние Q1
если ячейка содержит значения 0 или 1 выполняем команды 0RQ2 и 1RQ2
Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи
C точки зрения автомата:
- нахожусь в состоянии Q1
- считываю значения текущей ячейки
- если это 0 или 1 то продолжаю двигаться вправо и перехожу в состояние Q2
Автомат переходит в состояние Q2 (второй столбец), так как функция состояния Q1 — найти число находящегося на ленте, выполнена. Число на ленте найдено. Каретка теперь находится над числом и теперь необходимо найти его конец, для продолжения выполнения программы. Для этого продолжаем двигать каретку вправо, до тех пор, пока не наткнемся на пустую ячейку (означает конец числа на ленте) — команда ]LQ3, при выполнении которой автомат переходит в сотояние Q3.
| Q1 | Q2 | Q3 | |
| 0RQ2 | 0RQ2 | 1HQ0 | |
| 1 | 1RQ2 | 1RQ2 | 0LQ3 |
| ] | ]RQ1 | ]LQ3 | 1HQ0 |
Из таблицы видно, что автомат в состоянии Q3 выполняет арифметические действия над вводимым числом. Алгоритм для двоичного числа очень прост, считываем, и если это ноль, то заменим значение ячейки единицей и останавливаем программу, если единица, то меняем на ноль и переходим на шаг влево, где алгоритм повторяется для текущей ячейки, и так далее.
Задача 2.
Напишите программу для машины Тьюринга, которая проверяет любое введенное десятичное число на четность.
Решение:
С точки зрения автомата:
- нахожусь в состоянии — Q1
- если это цифра, то двигаю каретку на шаг вправо и перехожу в состояние — Q1
- если это пустая ячейка, то двигаю каретку на шаг влево и перехожу в состояние — Q2
- если эта цифра 0,2,4,6,8 — двигаю каретку на шаг вправо и перехожу в состояние — Q3
- в состоянии Q3 стою на месте, записываю букву Y и останавливаю программу — Q0
- если эта цифра 1,3,5,7,9 — двигаю каретку на шаг вправо и перехожу в состояние — Q4
- в состоянии Q4 стою на месте, записываю букву N и останавливаю программу — Q0
От автора:
Данная программа эмулятора была задумана лишь для изучения простейших алгоритмов. Сложные программы писать по Тьюрингу пустая трата времени.
Источник: goto7.ru
Рассмотрим пример решения одной задачи
Пример. Требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.
Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:
В этой машине Тьюринга q 1 — состояние изменения цифры, q 0 — состояние останова. Если в состоянии ql автомат видит цифру 0..8, то он заменяет ее на 1..9 соответственно и переходит в состояние q 0, т.е. машина останавливается. Если же он видит цифру 9, то заменяет ее на 0, сдвигается влево, оставаясь в состоянии ql. Так продолжается до тех пор, пока автомат не встретит цифру меньше 9. Если же все цифры были равны 9, то он заменит их нулями, запишет 0 на месте старшей цифры, сдвинется влево и в пустой клетке запишет 1. Затем перейдет в состояние q 0, т.е. остановится.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Студопедия рекомендует:
Понятие «неблагополучная семья», ее основные характеристики. Типология неблагополучных семей Многочисленные отечественные и зарубежные исследования показывают.
Лечебно-охранительный режим отделения В основе общепринятого режима лечебно-профилактического учреждения и его лечебных отделений лежат мероприятия.
Вопрос 2. Источники конституционного права Под источником права понимается форма, в которой существуют, выражаются правовые нормы.
Молярная концентрация эквивалента I. Эквивалент – это условная или реальная частица, которая в данной химической реакции эквивалентна одному атому или иону.
Важнейшие правовые и законодательные акты мирового и регионального значения. Акты международного права Система современного международного права сложилась после Второй мировой войны и принятия Устава ООНhttps://studopedia.ru/4_47405_rassmotrim-primer-resheniya-odnoy-zadachi.html» target=»_blank»]studopedia.ru[/mask_link]