Цель занятия: изучение основных операторов графики системы MATLAB и создание программ, реализующих графический вывод.
Основные теоретические сведения
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Для отображения функций одной переменной у (х) используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у (х). Поскольку MATLAB — матричная система, совокупность точек у (х) задается векторами X и Y одинакового размера.
#12. Как строить трехмерные графики | Matplotlib уроки
Команда plot (X, Y) служит для построения графиков функций в декартовой системе координат, координаты точек (х, у) берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Команда plot (X, Y, S) аналогична команде plot(X, Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы, которые представлены в таблице 4.1.
Таблица 4.1 Задание типа линии
Маркер типа линии
Маркер цвета графика
Продолжение таблицы 4.1
Продолжение таблицы 4.1
Тип проставляемой точки
Таким образом, с помощью строковой константы S можно изменять цвет линии, представлять узловые точки различными отметками (точка, окружность, крест, треугольник с разной ориентацией вершины и т. д.) и менять тип линии графика.
Команда р lot (X 1, Y 1, S 1, Х2, Y 2, S 2, ХЗ, Y3, S3. ) строит на одном графике ряд линий, представленных данными вида (X, Y, S), где X и Y — векторы или матрицы, a S — строки. С помощью такой конструкции возможно построение, например, графика функции линией, цвет которой отличается от цвета узловых точек. При отсутствии указания на цвет линий и точек он выбирается автоматически из таблицы цветов (белый исключается). Если линий больше шести, то выбор цветов повторяется.
Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливается с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.
Трехмерные поверхности обычно описываются функцией двух переменных z (x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц.
MatLab. Урок 3. Функции и построение графиков.
Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в следующих формах:
– [X,Y,Z] = meshgrid(x, y, z) — возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных графиков;
– [X,Y] = meshgrid (x, y) — преобразует область, заданную векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х, а столбцы Y — копиями вектора у.
Команда plot3 (. ) является аналогом команды plot(. ), но относится к функции двух переменных z (x, у). Она строит аксонометрическое изображение трехмерных поверхностей и представлена следующими формами:
– plot3 (x, y, z) — строит массив точек, представленных векторами х, у и z, соединяя их отрезками прямых. Эта команда имеет ограниченное применение;
– plot3 (X, Y, Z, S) — обеспечивает построения со спецификацией стиля линий и точек;
– plot3 (x1, y1, z1, s1, х2, у2, z2, s2. )— строит на одном рисунке графики нескольких функций z1 (x1, y1), z2 (x2, y2) и т. д. со спецификацией линий и маркеров каждой из них.
Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh. Имеются три группы таких команд:
– mesh (X, Y, Z, C) — выводит в графическое окно сетчатую поверхность Z (X, Y) с цветами узлов поверхности, заданными массивом С;
– mesh (X, Y, Z) — аналог предшествующей команды при C = Z.
В данном случае используется функциональная окраска, при которой цвет задается высотой поверхности. Функция mesh возвращает дескриптор для объекта класса surface. Ниже приводится пример применения команды mesh:
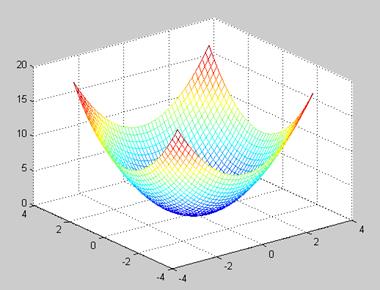
Рисунок 4.1 – График поверхности, созданный командой mesh(X,Y,Z)
После того как график уже построен, MATLAB позволяет выполнить его форматирование или оформление в нужном виде. Так, для установки над графиком титульной надписи используется следующая команда title (‘string ‘ ) — установка на двумерных и трехмерных графиках титульной надписи, заданной строковой константой ‘string’.
Для установки надписей возле осей х, у и z используются следующие команды: xlabel (‘String’), ylabe l (‘String’), zlabel (‘String’).

Рисунок 4.2 – Установка надписей с использованием команды:
xlabel(‘String’), ylabel(‘String’), zlabel(‘String’)
Часто возникает необходимость добавления текста в определенное место графика, например для обозначения той или иной кривой графика. Для этого используется команда text:
– text (X, Y, ‘string’) — добавляет в двумерный график текст, заданный строковой константой ‘string’, так что начало текста расположено в точке с координатами (X, Y). Если X и Y заданы как одномерные массивы, то надпись помещается во все позиции [ x (i), y (i)];
– text (X, Y, Z, ‘string’) — добавляет в трехмерный график текст, заданный строковой константой ‘string’, так что начало текста расположено в позиции, заданной координатами X, Y и Z.
Очень удобный способ ввода текста предоставляет команда gtext:
– gtext (‘string’) — задает выводимый на график текст в виде строковой константы ‘string’ и выводит на график перемещаемый мышью маркер в виде крестика. Установив маркер в нужное место, достаточно щелкнуть любой кнопкой мыши для вывода текста.
Пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него, называется легендой. Для создания легенды используются различные варианты команды legend:
legend (stringl, string2,…, strings) — добавляет к текущему графику легенду в виде строк, указанных в списке параметров;

Рисунок 4.3 – График с пояснениями
l egend (Pos) — помещает легенду в точно определенное место, специфицированное параметром Pos:
Pos=0 — лучшее место, выбираемое автоматически;
Pos=l — верхний правый угол;
Pos=2 — верхний левый угол;
Pos=3 — нижний левый угол;
Pos=4 — нижний правый угол;
Pos=-l — справа от графика.
При добавлении легенды следует учесть, что порядок и количество аргументов команды legend должны соответствовать порядку вывода графиков и их количеству
Обычно графики выводятся в режиме автоматического масштабирования. Следующие команды класса axis меняют эту ситуацию:
– axis ([XMIN XMAX YMIN YMAX]) — установка диапазонов координат по осям х и у для текущего двумерного графика;
– axis ([XMIN XMAX YMIN YMAX ZMIN ZMAX]) – установка диапазонов координат по осям х, у и z текущего трехмерного графика;
– axis auto — установка параметров осей по умолчанию;
В математической, физической и иной литературе при построении графиков в дополнение к разметке осей часто используют масштабную сетку. Команды grid позволяют задавать построение сетки или отменять это построение:
– grid on — добавляет сетку к текущему графику;
– grid off — отключает сетку.
Во многих случаях желательно построение многих наложенных друг на друга графиков в одном и том же окне. Для этого служит команда продолжения графических построений hold. Она используется в следующих формах:
– hold on — обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже существующим;
– hold off — отменяет режим продолжения графических построений;
Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков:
– subplot (m, n, p)— разбивает графическое окно на m × n подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а р — номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам).
Проиллюстрируем работу функции subplot (см рис. 4.4):
>>subplot(3, 2, 1); plot (x,y);
>> subplot(3, 2, 4); plot (x,y);
>> subplot(3, 2, 5); plot (x,y);
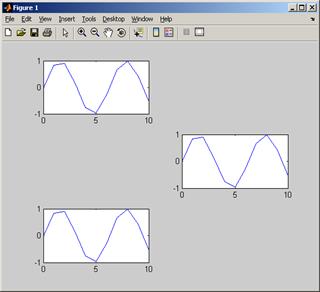
Рисунок 4.4 – Работа функции subplot
Было сформировано 3 строки и два столбца полей для вывода графиков. Обращение к каждому конкретному полю происходит с указанием его номера. Нумерация происходит слева направо и снизу вверх
Порядок выполнения
1. Составление и отладка программы для вывода графиков функций f 1, f 2, f 3 на основании задания из таблицы 4.2. Вывод графиков должен быть осуществлен в одном окне, графики должны быть подписаны, отмасштабированы.
Таблица 4.2 Варианты заданий
| Номер варианта | ||||
| 1 | 2 | 3 | 4 | 5 |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 |
2. Составление и отладка программы для вывода графика трехмерной поверхности для функции f 4 () задания из таблицы 4.2.
3. Написать файл-функцию для вычисления кусочно-заданной функции (табл. 4.3) и построить ее график.
Таблица 4.3 Варианты заданий кусочно-заданной функции
Продолжение таблицы 4.3
Содержание отчета
2. Листинг программы для вывода графиков функций.
4.4 Контрольные вопросы
1. С помощью какой команды осуществляется построение графиков декартовой системах координат?
2. Для чего служит команда mesh?
3. Как осуществляется задание надписей?
4. Для чего используется команда grid?
5. Как осуществляется разбивка окна на меньшие окна?
6. Для чего используется команда hold?
Практическая работа № 5


Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник: cyberpedia.su
Основные теоретические сведения. Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Для отображения функций одной переменной у(х) используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot (X, Y) служит для построения графиков функций в декартовой системе координат, координаты точек (х, у) берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Команда plot(X, Y, S) аналогична команде plot(X, Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы, которые представлены в таблице 4.1.
Таблица 4.1 Задание типа линии
| Маркер типа линии | |
| Маркет | Тип линии |
| — | Непрерывная |
| — | Штриховая |
| : | Пурктирная (точками) |
| -. | Штрих-пунктирная |
| Маркер цвета графика | |
| Продолжение таблицы 4.1 | |
| Маркер | Цвет графика |
| c | Голубой |
| m | Фиолетовый |
| y | Желтый |
| Продолжение таблицы 4.1 | |
| r | Красный |
| g | Зеленый |
| b | Синий |
| w | Белый |
| k | Черный |
| Тип проставляемой точки | |
| Маркер | Тип точки |
| . | Точка |
| + | Плюс |
| * | Звездочкой |
| о | Кружком (указывается латинская буква о) |
| х | Крестиком (указывается латинская буква x) |
Таким образом, с помощью строковой константы S можно изменять цвет линии, представлять узловые точки различными отметками (точка, окружность, крест, треугольник с разной ориентацией вершины и т. д.) и менять тип линии графика.
Команда рlot(X1, Y1, S1, Х2, Y2, S2, ХЗ, Y3, S3. ) строит на одном графике ряд линий, представленных данными вида (X, Y, S), где X и Y — векторы или матрицы, a S — строки. С помощью такой конструкции возможно построение, например, графика функции линией, цвет которой отличается от цвета узловых точек. При отсутствии указания на цвет линий и точек он выбирается автоматически из таблицы цветов (белый исключается). Если линий больше шести, то выбор цветов повторяется.
Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливается с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.
Трехмерные поверхности обычно описываются функцией двух переменных z(x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц.
Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в следующих формах:
– [X,Y,Z] = meshgrid(x, y, z) — возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных графиков;
– [X,Y] = meshgrid(x, y) — преобразует область, заданную векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х, а столбцы Y — копиями вектора у.
Команда plot3(. ) является аналогом команды plot(. ), но относится к функции двух переменных z(x, у). Она строит аксонометрическое изображение трехмерных поверхностей и представлена следующими формами:
– plot3(x, y, z) — строит массив точек, представленных векторами х, у и z, соединяя их отрезками прямых. Эта команда имеет ограниченное применение;
– plot3(X, Y, Z, S) — обеспечивает построения со спецификацией стиля линий и точек;
– plot3(x1, y1, z1, s1, х2, у2, z2, s2. )— строит на одном рисунке графики нескольких функций z1(x1,y1), z2(x2,y2) и т. д. со спецификацией линий и маркеров каждой из них.
Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh. Имеются три группы таких команд:
– mesh(X, Y, Z, C) — выводит в графическое окно сетчатую поверхность Z(X,Y) с цветами узлов поверхности, заданными массивом С;
– mesh(X, Y, Z) — аналог предшествующей команды при C=Z.
В данном случае используется функциональная окраска, при которой цвет задается высотой поверхности. Функция mesh возвращает дескриптор для объекта класса surface. Ниже приводится пример применения команды mesh:

Рисунок 4.1 – График поверхности, созданный командой mesh(X,Y,Z)
После того как график уже построен, MATLAB позволяет выполнить его форматирование или оформление в нужном виде. Так, для установки над графиком титульной надписи используется следующая команда title( ‘string ‘ ) — установка на двумерных и трехмерных графиках титульной надписи, заданной строковой константой ‘string’.
Для установки надписей возле осей х, у и z используются следующие команды: xlabel(‘String’), ylabel(‘String’), zlabel(‘String’).

Рисунок 4.2 – Установка надписей с использованием команды:
xlabel(‘String’), ylabel(‘String’), zlabel(‘String’)
Часто возникает необходимость добавления текста в определенное место графика, например для обозначения той или иной кривой графика. Для этого используется команда text:
– text(X,Y, ‘string’) — добавляет в двумерный график текст, заданный строковой константой ‘string’, так что начало текста расположено в точке с координатами (X, Y). Если X и Y заданы как одномерные массивы, то надпись помещается во все позиции [x(i), y(i)];
– text(X,Y, Z, ‘string’) — добавляет в трехмерный график текст, заданный строковой константой ‘string’, так что начало текста расположено в позиции, заданной координатами X, Y и Z.
Очень удобный способ ввода текста предоставляет команда gtext:
– gtext(‘string’) — задает выводимый на график текст в виде строковой константы ‘string’ и выводит на график перемещаемый мышью маркер в виде крестика. Установив маркер в нужное место, достаточно щелкнуть любой кнопкой мыши для вывода текста.
Пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него, называется легендой. Для создания легенды используются различные варианты команды legend:
legend(stringl, string2,…, strings) — добавляет к текущему графику легенду в виде строк, указанных в списке параметров;

Рисунок 4.3 – График с пояснениями
legend (Pos) — помещает легенду в точно определенное место, специфицированное параметром Pos:
Pos=0 — лучшее место, выбираемое автоматически;
Pos=l — верхний правый угол;
Pos=2 — верхний левый угол;
Pos=3 — нижний левый угол;
Pos=4 — нижний правый угол;
Pos=-l — справа от графика.
При добавлении легенды следует учесть, что порядок и количество аргументов командыlegend должны соответствовать порядку вывода графиков и их количеству
Обычно графики выводятся в режиме автоматического масштабирования. Следующие команды класса axis меняют эту ситуацию:
– axis([XMIN XMAX YMIN YMAX]) — установка диапазонов координат по осям х и у для текущего двумерного графика;
– axis([XMIN XMAX YMIN YMAX ZMIN ZMAX]) – установка диапазонов координат по осям х, у и z текущего трехмерного графика;
– axis auto — установка параметров осей по умолчанию;
В математической, физической и иной литературе при построении графиков в дополнение к разметке осей часто используют масштабную сетку. Команды grid позволяют задавать построение сетки или отменять это построение:
– gridon — добавляет сетку к текущему графику;
– grid off — отключает сетку.
Во многих случаях желательно построение многих наложенных друг на друга графиков в одном и том же окне. Для этого служит команда продолжения графических построений hold. Она используется в следующих формах:
– hold on — обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже существующим;
– hold off — отменяет режим продолжения графических построений;
Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков:
– subplot(m, n, p)— разбивает графическое окно на m×n подокон, при этом m — число подокон по горизонтали, n— число подокон по вертикали, а р — номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам).
Проиллюстрируем работу функции subplot (см рис. 4.4):
>>subplot(3, 2, 1); plot (x,y);
>> subplot(3, 2, 4); plot (x,y);
>> subplot(3, 2, 5); plot (x,y);
 Рисунок 4.4 – Работа функции subplot Рисунок 4.4 – Работа функции subplot |
Было сформировано 3 строки и два столбца полей для вывода графиков. Обращение к каждому конкретному полю происходит с указанием его номера. Нумерация происходит слева направо и снизу вверх
Порядок выполнения
1. Составление и отладка программы для вывода графиков функций f1, f2, f3 на основании задания из таблицы 4.2. Вывод графиков должен быть осуществлен в одном окне, графики должны быть подписаны, отмасштабированы.
Таблица 4.2 Варианты заданий
| Номер варианта |
2. Составление и отладка программы для вывода графика трехмерной поверхности для функции f4 ( ) задания из таблицы 4.2.
3. Написать файл-функцию для вычисления кусочно-заданной функции (табл. 4.3) и построить ее график.
Таблица 4.3 Варианты заданий кусочно-заданной функции
| № варианта | Функция | № варианта | Функция |
| Продолжение таблицы 4.3 |
Содержание отчета
2. Листинг программы для вывода графиков функций.
Контрольные вопросы
1. С помощью какой команды осуществляется построение графиков декартовой системах координат?
2. Для чего служит команда mesh?
3. Как осуществляется задание надписей?
4. Для чего используется команда grid?
5. Как осуществляется разбивка окна на меньшие окна?
6. Для чего используется команда hold?
Практическое занятие № 5
Источник: allrefrs.ru
Построение трёхмерных графиков
Рассмотрим построение графиков функций двух переменных на прямоугольной области определения. Предположим, что требуется получить поверхность функции  на прямоугольнике x
на прямоугольнике x  [-1, 1], y
[-1, 1], y  [0, 2]. Первый шаг состоит в задании сетки на прямоугольнике, то есть точек, которые будут использоваться для вычисления значений функции. Для генерации сетки предусмотрена функция meshgrid, вызываемая от двух входных аргументов – векторов, задающих разбиения по осям x и y. Функция meshgrid возвращает два выходных аргумента, являющихся матрицами:
[0, 2]. Первый шаг состоит в задании сетки на прямоугольнике, то есть точек, которые будут использоваться для вычисления значений функции. Для генерации сетки предусмотрена функция meshgrid, вызываемая от двух входных аргументов – векторов, задающих разбиения по осям x и y. Функция meshgrid возвращает два выходных аргумента, являющихся матрицами:
Матрица X состоит из одинаковых строк, равных первому входному аргументу – вектору в meshgrid, а матрица Y – из одинаковых столбцов, совпадающих со вторым вектором в meshgrid. Такие матрицы оказываются необходимыми на втором шаге при заполнении матрицы Z, каждый элемент которой является значением функции z (x, y) в точках сетки. Несложно понять, что использование поэлементных операций при вычислении функции z (x, y) приводит к требуемой матрице:
Для построения графика z (x, y) осталось вызвать подходящую графическую функцию, к примеру:
На экране появляется графическое окно, содержащее каркасную поверхность исследуемой функции (рис. 3.11). Обратите внимание, что цвет поверхности соответствует значению функции.
Команда colorbar приводит к отображению в графическом окне столбика, показывающего соотношение между цветом и значением z (x, y). Цветовые палитры графика можно изменять, пользуясь функцией colormap, например, colormap(gray) отображает график в оттенках серого цвета. Некоторые цветовые палитры приведены ниже:
· bone – похожа на палитру gray, но с легким оттенком синего цвета;
· colorcube – каждый цвет изменяется от темного к яркому;
· cool – оттенки голубого и пурпурного цветов;
· copper – оттенки медного цвета;
· hot – плавное изменение: черный-красный-оранжевый-жёлтый-белый;
· hsv – плавное изменение (как цвета радуги);
· jet – плавное изменение: синий-голубой-зелёный-жёлтый-красный;
· spring – оттенки пурпурного и жёлтого;
· summer – оттенки зелёного и жёлтого;
· winter – оттенки синего и зелёного;
MATLAB предоставляет целый набор графических функций для визуализации функций двух переменных, среди них:
o surf – залитая цветом каркасная поверхность;
o meshc, surfc – поверхности с линиями уровня на плоскости xy;
o contour – плоский график с линиями уровня;
o contourf – залитый цветом плоский график с линиями уровня;
o contour3 – поверхность, составленная из линий уровня;
o surfl – освещённая поверхность.
Все перечисленные функции допускают то же самое обращение, что и mesh, например:
Остановимся подробнее на нескольких вопросах. Первый из них: как изменять установки, определённые по умолчанию, при отображении функций линиями уровня при помощи contour, contourf и contour3. Число линий уровня задаётся в четвёртом дополнительном аргументе, например:
Вместо числа линий уровня можно указать в векторе те значения z (x, y), для которых требуется построить линии уровня:
>> contour(X,Y,Z,[-0.51 -0.25 -0.01 0.89]).
Несколько сложнее нанести подписи с соответствующим значением z (x, y) к каждой линии уровня. Для этого придётся вызвать contour с двумя выходными аргументами, первый из них – матрица с информацией о положении линий уровня, а второй – вектор с указателями на линии (рис.3.12). Полученные переменные следует использовать в качестве входных аргументов функции clabel:
>> [CMatr, h] = contour(X, Y, Z,[-0.51 -0.25 -0.01 0.89]);
Залитые цветом каркасные поверхности, построенные при помощи surf и surfc, имеют постоянный цвет в пределах каждой ячейки. Команда shading interp, вызываемая после surf и surfc, служит для плавного изменения цвета в пределах ячеек и скрытия линий сетки на поверхности. Если желательно убрать сетку и сохранить постоянный цвет ячеек, то достаточно использовать shading flat, а shading faceted придаёт графику прежний вид.
Столь же просто обеспечивается построение графиков сложных поверхностей. Надо только знать, какой командой реализуется тот или иной график. Например, для построения графика поверхности и её проекции в виде контурного графика на плоскость под поверхностью достаточно использовать следующие команды:
Окно с построенным графиком показано на рис. 3.13.

Рис. 3.13.Окно с графиками поверхности и её проекции на плоскость под фигурой
Раньше пришлось бы потратить немало времени на составление и отладку нужной для построения такого графика программы. В MATLAB же можно в считанные секунды изменить задающую поверхность функцию Z(X, Y) и тут же получить новый график поверхности с окраской, в данном случае заданной вектором Z, и с её проекцией на плоскость XY.