Составить циклический алгоритм и программу для вычисления

Алгоритм называется циклическим, если он содержит многократное выполнение одних и тех же ветвей при различных значениях промежуточных данных. Число повторений этих ветвей алгоритма может быть задано в явной или неявной форме.

Перед выполнением работы необходимо изучить различные схемы организации циклов и операторы FOR, WHILE и REPEAT, с помощью которых они программируются.

Пример. Составим программу для вычисления и вывода на печать таблицы значений функции y = a x 2 при x = 5, 6, 7. 35; a =10.2.

С использованием оператора WHILE программа имеет вид:

С использованием REPEAT программа выглядит так:

Порядок выполнения работы

1. Изучить необходимые сведения, указанные в п.3.

2. Получить у преподавателя вариант задания.

3. Разработать, ввести и отладить программу

4. Произвести расчет по крайней мере при двух различных вариантах исходных данных, выбранных самостоятельно.

5. Оформить отчет, защитить и сдать его преподавателю. Отчет должен содержать цель работы, задание, блок-схему программы, распечатку программы и результатов прогона программы.

Блок-схемы для начинающих (Блок схемы алгоритмов)

Варианты заданий

1. Вычислить число сочетаний из n по m по формуле

где n!=1*2*3…(n-1)*n, целые числа n, m (n>=m>0) ввести с клавиатуры.

2. Вычислить значение выражения

где n ввести с клавиатуры.

3. Вычислить число размещений из n по m по формуле

где целые числа n и m ввести с клавиатуры (n>=m>0).

4. Вычислить приближенно значение бесконечной суммы с точностью до e = 0,001;

Значение n и точность расчетов ввести с клавиатуры.

Примечание. Считать, что требуемая точность достигнута, если очередное слагаемое оказалось по модулю меньше,чем e.

5. Вычислить приближенно значение бесконечной суммы с точностью до 0,0005:

Значение n и точность расчетов ввести как константы (см. примечание к варианту 4).

6. Дано натуральное n, определить количество цифр в числе n и сумму всех его цифр. Значение n ввести с клавиатуры.

7. Вывести на печать таблицу n значений функции при изменении х от х1 до х2 с шагом h = (х2- х1)/(n – 1). Коэффициенты a, b, c, границы интервала х1, х2 и число n ввести с клавиатуры.

8. Вычислить значение функции для k = 1,2,….Вычисления производить до тех пор, пока y>=z. Исходные данные x, y и z (x, y>1) ввести с клавиатуры.

9. Найти приближенно, с точностью до 0,01, минимум функции f(x)= ax 2 + bx + c на отрезке х1 £ х 2. Значения х1, х2 и a, b, c ввести как константы.

11. Вычислить бесконечную сумму с точностью e=0,001.

См. примечание к варианту 4.

12. Вычислить бесконечную сумму с точностью e=0,001.

См. примечание к варианту 4.

13. Вычислить и вывести на экран таблицу значений функции у = х/k!, больших e, если k = 1,2,3,…. Исходные данные: х=1,55; e = 0,0183.

15. Вычислить значение выражения

(9 + (9 + …+ (9 + 9 1/2 ) 1/3 …) 1/ m-1 ) 1/m

Число m ввести с клавиатуры.

16. Составить программу для вычисления и вывода на экран таблицы значений сумм для а £ х £ b, изменяющегося с шагом h = (b-a)/10. Исходные данные: а = -1,05; b= 362; n = 10.

17. Вычислить и вывести на экран таблицу значений функции у = x 2 – ab – cx для х = -5, -6, -7,…,-35. Исходные данные (в экспоненциальной форме записи): а = 1,14Е +1; b = -4,21Е+2; с = 3,25Е+3.

18. Составить программу вычисления и вывода на экран таблицы сумм , где х изменяется в пределах а £ х £ b с шагом h = (b-a)/10. Исходные данные: а = 0,1; b = 13; n = 12.

19. Вычислить и вывести на экран таблицу значений функции у = x 2 – ab + cx, для хнач. £ х £ хкон. с шагом h. Исходные данные: а = -1,14; b = -4,21; с = 3,25; хнач.= 4,5; хкон = 35,5; h = 0,5.

20. Найти наибольшее значение функции у = аx 3 + bх – c при изменении х от хнач. до хкон с шагом h. Исходные данные: а = 2,14; b = -4,21; с = 3,25; хнач.= — 4,5; хкон = — 35,5; h = — 0,5.

21. Вычислить приближенно значение бесконечной суммы с точностью до 0,0005:

Значение n и точность расчетов ввести как константы (см. примечание к варианту 4).

22. Дано натуральное n, определить количество цифр в числе n и сумму всех его цифр. Значение n ввести с клавиатуры.

23. Вывести на печать таблицу n значений функции при изменении х от х1 до х2 с шагом h = (х2- х1)/(n – 1). Коэффициенты a, b, c, границы интервала х1, х2 и число n ввести с клавиатуры.

24. Вычислить значение функции для k = 1,2,…. Вычисления производить до тех пор, пока y>=z. Исходные данные x, y и z (x, y>1) ввести с клавиатуры.

25. Найти приближенно, с точностью до 0,01, минимум функции f(x)= ax 2 + bx + c на отрезке х1 £ х 2. Значения х1, х2 и a, b, c ввести как константы.

27. Вычислить бесконечную сумму с точностью e=0,001.

См. примечание к варианту 4.

28. Вычислить бесконечную сумму с точностью e=0,001.

См. примечание к варианту 4.

29. Вычислить и вывести на экран таблицу значений функции у = х/k!, больших e, если k = 1,2,3,…. Исходные данные: х=1,55; e = 0,0183.

31. Вычислить значение выражения

(9 + (9 + …+ (9 + 9 1/2 ) 1/3 …) 1/ m-1 ) 1/m

Число m ввести с клавиатуры.

Контрольные вопросы.

1. Каково назначение режимов Compile и Tools системы Turbo?

2. Какие команды имеются в режимах Compile и Tools?

3. Как записывается и как работает оператор FOR?

4. Для организации каких циклов применим оператор FOR?

5. В чем отличие оператора WHILE от оператора REPEAT?

6. Как программируются циклические алгоритмы с явно заданным числом повторений цикла?

7. Как программируются циклические алгоритмы с незаданным числом по­вторений цикла?

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru

Составить циклический алгоритм и программу для вычисления

: 11

TP

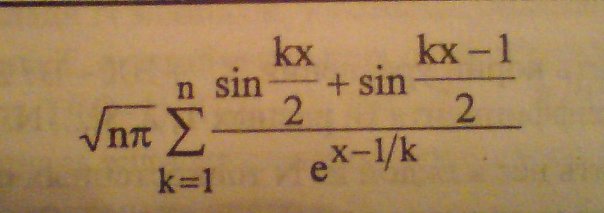
Вот с этой задачей ваще не че не пойму. Составить циклический алгоритм и программу для вычисления результата по формуле. Для проверки программы задать X=0.5; n=20.

Высокая репутация

СуперМодератор

: 16,107

Все просто: цикл for от 1 до n. А далее накапливаете в цикле сумму, затем умножаете ее на корень и готово

Заблокирован

: 11

я даже блок схему для нее нарисовать не могу, а надо же проверку сделать чтобы знаменатель был больше нуля

Высокая репутация

СуперМодератор

: 16,107

А знаменатель и не может быть < 0.

Заблокирован

: 11

а ты не можешь код написать чтоб мне было хоть с чем сравнивать.

Высокая репутация

СуперМодератор

: 16,107

Код должны Вы сами писать, за Вас этого ни кто делать не будет. Разбирайтесь, там ничего сложного.

Заблокирован

: 11

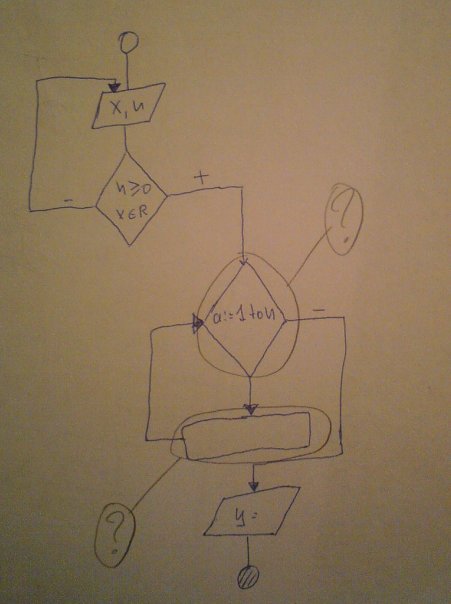
вот это правильно? и что надо где знаки вопроса?

Источник: www.programmersforum.ru

Программирование алгоритмов циклической структуры.

Цель работы:изучить операторы цикла и приобрести практическиенавыки в программировании алгоритмов циклической структуры.

1. Изучить операторы цикла языка Бейсик и особенности их при-

2. Для заданного варианта составить схему алгоритма циклической структуры и реализующие его программы с использованием условного опе-ратора и операторов цикла.

3. Произвести на ЭВМ расчеты по разработанным программам для исходных данных, приведенных в табл. 4.1, и сравнить результаты расчетов.

4. Получить распечатки программ и результатов расчета.

5. Оформить отчет по лабораторной работе.

Указания по выполнению работы

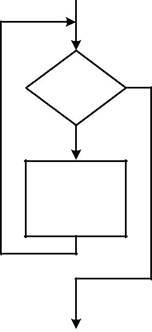
Алгоритм циклической структуры включает в себя одну из основных структур — цикл, который бывает двух типов: цикл До и цикл Пока (рис.4.1). В цикле До тело цикла выполняется до проверки некоторого условия “да” — ус-ловие истинно, “нет ” — условие ложно. Телом цикла называется последова-тельность действий, выполняемых в цикле многократно. В цикле Пока про-верка условия производится до выполнения тела цикла.

При программировании алгоритмов циклической структуры следует иметь в виду, что в цикле Пока при истинности условия, тело цикла не вы-полняется ни разу, а в цикле До оно всегда выполняется хотя бы один раз, независимо от условия. Цикл До рекомендуется использовать в задачах с за-ранее известным числом повторений цикла, цикл Пока — когда число повто-рений цикла заранее неизвестно, например, в расчетах до получения резуль-тата с заданной точностью.

Организация циклов в программах может осуществляться с помощью условного оператора (рис.4.1), рассмотренного в лабораторной работе № 3. или специальных операторов цикла.

Оператор цикла F0R-NEXT.

Оператор F0R-NEXT позволяет организовать выполнение блока опе-раторов определенное количество раз. Оператор F0R-NEXT имеет сле-дующую форму:

FOR счетчик = начало TO конец [STEP шаг] [операторы цикла]

[EXIT FOR] [операторы цикла] NEXT счетчик,

где счетчик – числовая переменная, используемая как счетчик цикла; начало – начальное значение счетчика; конец – конечное значение счетчика; шаг – шаг изменения значения счетчика по умолчанию равен 1; операторы цикла – набор операторов предназначенных для повторения.

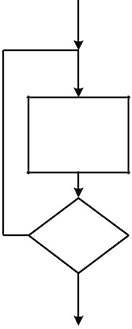
1. Операторы тела цикла

2. Есливыполняется перейти к п.1

1. Есливыполняется перейти к п.4

2. Операторы тела цикла

Рис.4.1. Виды циклов и их программирование с использованием ус-ловного оператора IF:

а — структура цикла До; б — структура цикла Пока.

Цикл F0R-NEXT выполняется до тех пор, пока текущее значение счет-чика не превышает его конечного его конечного значения. При завершении текущего цикла к значению счетчика прибавляется значение шага. Если конец

меньше начала, то шаг должен быть отрицательным. Если начало и конец имеют одно и тоже значение то цикл выполняется один раз вне зависимости от значения шага.

В качестве примера на рис.4.2 приведены алгоритм и программа вы-числения факториала Р = n! с оператором FOR-NEXT.

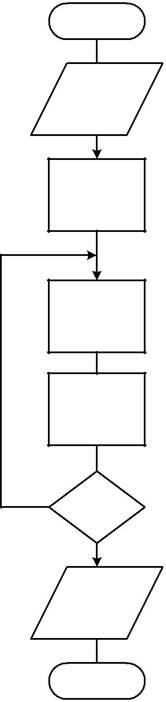
REM Программа вычисления n! REM с применением оператора цикла PRINT “Введите значение n=”; INPUT N

FOR I=1 TO N P=P*I

PRINT “Значение ”; N;”!=”;P END

Рис.4.2. Пример программирования циклического алгоритма:

а — схема алгоритма; б — его программная реализация с

применением операторов цикла

Решение приведенной задачи сводится к организации цикла, при каж-дом прохождении которого значение произведения Р умножается на очеред-ной сомножитель i. До входа в цикл необходимо задать Р=1. Для организации цикла в программах используется переменная I. При превышении этой пере-менной значения N происходит выход из цикла и вывод результатов расчета на дисплей.

Варианты заданий к лабораторной работе № 4

№	Составить программу табулирования функции y на	Исходные данные
п.п.	отрезке [a,b] с шагом h	a	b	h
1.	y = x /( x2+1)	4,0	6,0	0,2
2.	y = x /( x3+1)	3,0	5,0	0,25
3.	y =	x / x3	1,0	10,0	1,0
4.	y = x ln x2	2,5	3,5	0,1
5.	y =ln( x +1) /( x2+1)	2,0	6,0	0,5
6.	y = e x /( x2+2)	1,2	2,1	0,1
7.	y =2sin2 x /(1+ x3)	3,14	0,31
8.	y =cos x /(1+ x3)	1,57	3,14	0,16
9.	y =5sin x /(1+ x2)	4,3	5,5	0,2
y =(1?cos2 x ) /(0,5 x +1)	1,5	2,5	0,1
Составить программу вычисления k членов последовательности
№	Формула общего члена	k	№	Формула общего члена	k
п.п	п.п
11.	ak	= k 2 /( k 3 +2)	12.	ak	= ( k 2 +10) / 2k
13.	a k	=	k /( k +1)	14.	a k	= k /( k 2 +2)
15.	ak	= (2 k +1) / k 2	16.	ak	= k k ?1 /( k +5)
Составить программу вычисления суммы k членов последовательности
№	Формула общего члена	k	№	Формула общего члена	k
п.п	п.п
17.	a k	=	k /( k +3)	18.	ak	= ( k +1) / k 2
19.	ak	= k 2 /( k 2 +5)	20.	ak	= k 2 /( k 3 +1)
21.	ak	= k 2 / 2k	22.	ak	= (5k +3) / ek

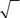Составить программу вычисления произведения k членов последовательности

№	Формула общего члена	k	№	Формула общего члена	k
п.п	п.п
23.	ak	= k 3 /( k +1)	24.	ak =(2 k +1)	/ 5k 2
25.	ak	= (2 k +1) / k 3	26.	ak =(2 k +1)	/ k 3
27.	ak	= k /(2 k +1)	28.	ak =5k /( ek +1)
29.	a k	= k /( k 3 ?1)	30.	ak = e k /(3k 2+1)

Лабораторная работа №5

Статьи к прочтению:

• Программирование алгоритмов с итерационными циклами
• Программы с линейной структурой

Найти общий член числового ряда — bezbotvy

Похожие статьи:

• Тема.5. программирование алгоритмов разветвляющейся структуры Цели работы:Познакомить читателя со встроенными возможностями пакета MathCAD для линейного программирования, а также для разветвляющегося вычислительного…
• Программирование алгоритмов разветвляющей структуры Контрольные вопросы: 1. Что такое алгоритм разветвляющей структуры? 2. Какие виды разветвления вы знаете? 3. Когда используется оператор безусловного…

Источник: csaa.ru