Тема: Табулирование функции. Применение табулирования к решению уравнения f(x)= 0.
Цель работы: составление программы табулирования функции y = f(x) и ее использование для нахождения корня уравнения f(x)= 0 с заданной точностью.
Варианты заданий лабораторной работы №3 приведены в таблице 3.1.
Работа состоит из двух задач:
Задача 1. Найти таблицу значений функций y = f(x) на отрезке [ a, b ] с шагом h.
Задача 2. Вычислить корень уравнения f(x) = 0 на отрезке [ a, b ] с точностью e=0,005.
Перед выполнением задания любого уровня необходимо проверить графически, что на заданном отрезке [ a, b ] находится корень уравнения. Если корня на заданном отрезке нет, то следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его. График привести в отчёте.
Задание (1 уровень)
1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
Excel график функции
2. Составить блок-схему алгоритма табулирования функции f(x) на отрезке [ a, b ] с шагом h =0,1.
3. Составить программу табулирования функции f(x) на отрезке [ a, b ] с шагом h =0,1.
4. Ввести программу, выполнить её, получить и выписать 11 пар значений (x, y).
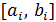
5. Для вычисления корня уравнения f(x) = 0 найти и выписать отрезок , полученный в результатах табулирования, на концах которого f(x) имеет разные знаки.
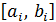
6. Повторно запуская программу табулирования, получить таблицу значений функции f(x) на отрезке с шагом h =0,1.
7. С экрана выписать новый отрезок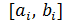 
, на концах которого функция f(x) имеет разные знаки. Вычислить середину этого отрезка 
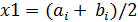– это и будет приближённый корень уравнения f(x)=0, с точностью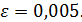 
8. Вычислить значение функции в корне. Выписать полученные результаты.
Задание (2 уровень)
1. Графически получить приближенное решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
2. Изменить блок-схему задачи табулирования функции f(x), предусмотрев возможность повторного запуска алгоритма табулирования на новом интервале с новым шагом h (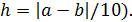 
Выход из программы должен быть выполнен, если длина найденного интервала окажется меньше либо равна заданной погрешности e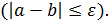 
3. Составить программу табулирования f(x) на [ a, b ] с шагом h по новой блок-схеме.
4. Запустить программу, получить результаты по табулированию функции f(x) последовательно на данном интервале [ a, b ] с шагом h =0,1 и на каждом новом интервале 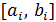, где функция меняет знак на противоположный, с шагом 
.
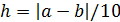5. С экрана выписать результаты табулирования на первом интервале, а для последующих результатов – выписывать две строки, где функция меняет свой знак. Выписать корень уравнения и значение функции в корне.
Задание (3 уровень)
1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
2. Составить блок-схему и программу, реализующие алгоритм вычисления корня уравнения f(x)= 0 на интервале [ a, b ] с заданной точностью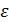 
. Для нахождения корня использовать алгоритм табулирования функции f(x), последовательно уменьшая в 10 раз интервал поиска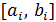
пока не выполнится условие: 
.
Замечания:
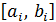
а) на каждом отрезке проводить не более 10 вычислений значений функции f(x);
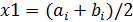
б) приближенным решением уравнения считать середину последнего отрезка .
3. Ввести программу, выполнить её и получить результат. На экран вывести границы каждого нового интервала поиска корня, корень уравнения, заданную точность и значение функции в корне.
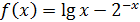
Задача 1. Найти таблицу значений функций y = f(x ) на отрезке [ a, b ] с шагом h =0.1, где , a =1, b =2.
Задача 2. Найти корень уравнения f(x) = 0 на отрезке [ a, b ] с точностью
e= 0.005.
Порядок выполнения задания (1 уровень)
1. Решение уравнения графическим методом.
1.1. Проверим графически, что на заданном отрезке [ a, b ] есть корень уравнения f(x)= 0, т.е.
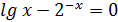
. (1)
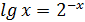
Перепишем уравнение (1):
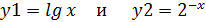
Построим два графика (рис. 3.1)
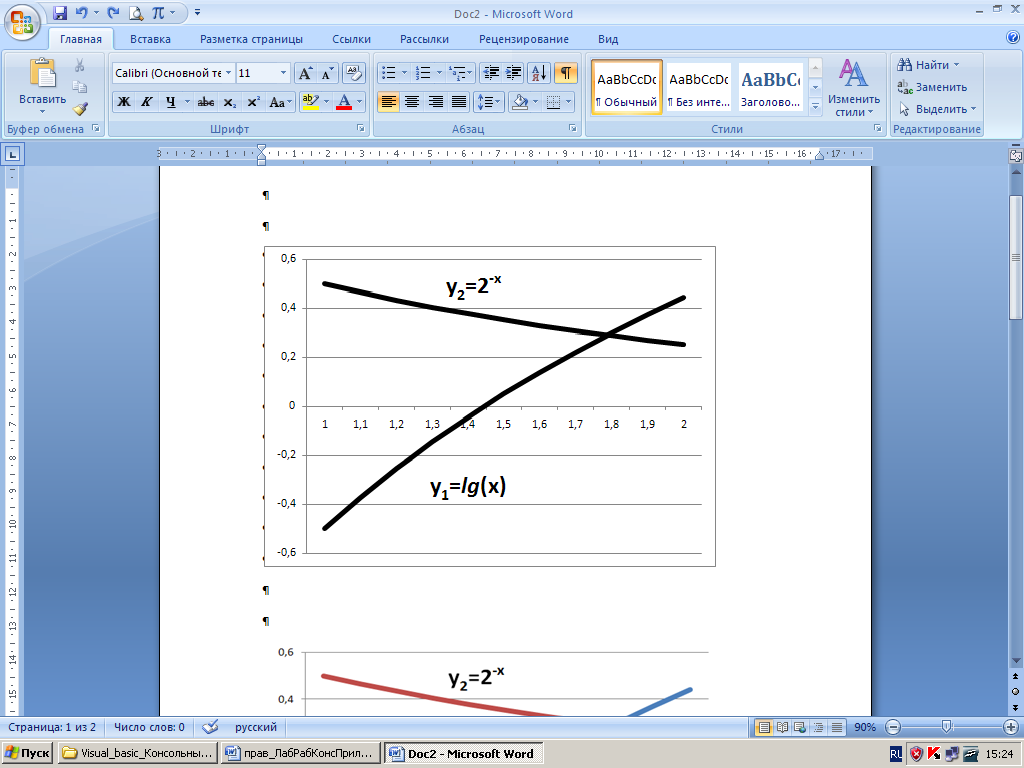
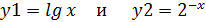
Рис. 3.1. Пересечение графиков
Графики пересекаются друг с другом в точке М. Абсцисса точки М (X * ) – есть корень уравнения
1.2. Если на заданном в условии отрезке графики не пересекаются, то это означает, что данный отрезок не содержит корня уравнения. В этом случае следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его.
2. Составление блок-схемы задачи табулирования.
2.1. Входные данные: a, b – границы отрезка, h — шаг.
Выходные данные: 11 пар значений (x, y).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAUwHCU8IA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPQYvCMBSE7wv7H8Jb8LKsqSKydI1SCqIHYdHV+6N5 tsXkpSTR1n9vhAWPw8x8wyxWgzXiRj60jhVMxhkI4srplmsFx7/11zeIEJE1Gsek4E4BVsv3twXm 2vW8p9sh1iJBOOSooImxy6UMVUMWw9h1xMk7O28xJulrqT32CW6NnGbZXFpsOS002FHZUHU5XK2C 350pvSmp35T30/Z4mhWfu3mh1OhjKH5ARBriK/zf3moFM3heSTdALh8AAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBTAcJTwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA «>
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAZsxCcMIA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wt+h/AEb2uq4LJWo6hQ8SLL+gevj+a1 KTYvpYlav/1mQfA4zMxvmPmys7W4U+srxwpGwwQEce50xaWC0zH7/AbhA7LG2jEpeJKH5aL3McdU uwf/0v0QShEh7FNUYEJoUil9bsiiH7qGOHqFay2GKNtS6hYfEW5rOU6SL2mx4rhgsKGNofx6uFkF m/WlzM7Nz37bmUudVfsim04KpQb9bjUDEagL7/CrvdMKJvB/Jd4AufgDAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBmzEJwwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA «>
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAQCjn8sQA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE70L/w/IK3nRTpa1GV6lCpBcRreL1kX3J BrNvQ3bV9N93C4LHYWa+YebLztbiRq2vHCt4GyYgiHOnKy4VHH+ywQSED8gaa8ek4Jc8LBcvvTmm 2t15T7dDKEWEsE9RgQmhSaX0uSGLfuga4ugVrrUYomxLqVu8R7it5ShJPqTFiuOCwYbWhvLL4WoV rFfnMjs1u+2mM+c6q7ZFNn0vlOq/dl8zEIG68Aw/2t9awfgT/r/EHyAXfwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAEAo5/LEAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA container»>
| a, b, h |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAWip1C8AA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QpuBk11BpFqlFIYdCEM42N/aa5t MbkpScbWvzeLgVkeznuzG6wRD/KhdaxgPstAEFdOt1wruJy/pisQISJrNI5JwZMC7Lajtw3m2vX8 Q49TrEUK4ZCjgibGLpcyVA1ZDDPXESfu5rzFmKCvpfbYp3Br5CLLltJiy6mhwY7Khqr76dcq+D6a 0puS+n35vB4u18/i/bgslJqMh2INItIQ/8V/7oNW8JHGpi/pB8jtCwAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEAWip1C8AAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA= container»>
| конец |
2.2. Блок – схема (рис. 3.2):
Рис. 3.2. Блок-схема алгоритма табулирования
3. Составление программы по блок-схеме из п.2.
3.1. Объявить переменные A, B, H, Y, X одинарной точности вещественного типа (Single).
3.2. Запросить ввод исходных данных с клавиатуры (Console.WriteLine()).
3.3. Открыть цикл для вычисления значения функции Y для аргумента X, изменяющегося от A до B с шагом H (For X = A To В Step H).
3.4. В цикле вычислить и вывести на экран значение функции Y(X) и соответствующего аргумента X.
3.5. Закрыть цикл (Next X) и завершить программу.
4. Выполнить программу и выписать результаты в отчёт (по аналогии с рис. 3.3).
| x = 1 | y = — 0.5 | x = 1.6 | y = — 0.126 |
| x = 1.1 | y = — 0.425 | x = 1.7 | y = — 0.77 |
| x = 1.2 | y = — 0.356 | x = 1.8 | y = — 0.032 |
| x = 1.3 | y = — 0.292 | x = 1.9 | y = 1.08 E-02 |
| x = 1.4 | y = — 0.232 | x = 2 | y = 5.10 E-02 |
| x = 1.5 | y = — 0.177 |
Рис. 3.3. Результаты: 11 пар значений (x, y)
5. Из таблицы значений, полученной в п.4, найти и выписать отрезок, на котором функция f(x) меняет свой знак. В данном случае это отрезок [ 1.8, 1.9 ], т.к. f(1.8) 0, а f(1.9)> 0.
6. На найденном отрезке [ 1.8, 1.9 ] запустить программу табулирования функции f(x) с шагом h =0.01.
7. Из полученных результатов найти и выписать две строки, где функция f(x) меняет знак:
x = 1.87 y = — 1.732Е-08 f(x) 0
x = 1.88 y= 2.474Е-03 f(x) > 0
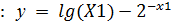
8. Вычислить середину выбранного отрезка [1.87, 1.88]: X1 =(1.87+1.88)/2 = 1.875 и значение функции в корне X1 (y = 3.743E-04).
9. Выписать результаты: значение корня (X1), значение функции в корне (y(X1)).
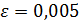
Вывод: значение X1 =1.875 является приближённым значением корня уравнения с точностью .
Пояснения к выполнению задания второго уровня
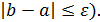
Для реализации выхода из программы выполнить проверку длины найденного отрезка ( Если это условие не выполняется, то программа должна запросить границы следующего отрезка, на котором функция имеет разные знаки на концах отрезка. Взять границы отрезка с экрана из результатов табулирования на предыдущем отрезке. Если условие выполняется, то необходимо в программе вычислить корень уравнения и значение функции в корне.
Пояснения к выполнению задания третьего уровня
Для поиска в программе нового отрезка табулирования выполнять проверку условия . Для выхода из программы сравнивать длину найденного отрезка с заданной точностью. Перед выходом из программы вычислить корень уравнения и значение функции в корне.
Таблица 3.1. Варианты заданий к лабораторной работе № 3
| № вар. | Уравнение | Отрезок [а, b] | № вар. | Уравнение | Отрезок [а,b] |
 |
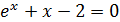[0;1] |  |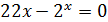
[0;1] | ||
 |
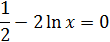[1;2] |  |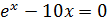
[3;4] | ||
 |
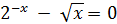[0.1;1.1] |  |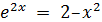
[-1;0] | ||
 |
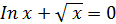[0.1;1.1] |  |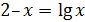
[1;2] | ||
 |
[2;3] |  |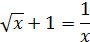
[0.1;1.1] | ||
 |
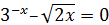[0;1] |  |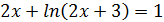
[0;1] | ||
 |
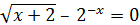[-2;-1] |  |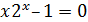
[0;1] | ||
 |
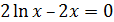[0.1;1.1] |  |
[1;2] | ||
 |
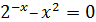[0;1] |  |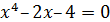
[1;2] | ||
 |
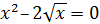[-0.5;0.5] |  |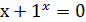
[-1;0] | ||
 |
[0.1; 1.1] |  |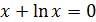
[2;3] | ||
 |
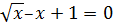[0.2;1.2] |  |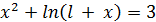
[0;1] | ||
 |
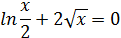[0.1; 1,1] |  |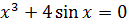
[-0.5; 0.5] | ||
 |
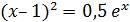[0;1] |  |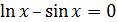
[2; 3] | ||
 |
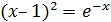[1;2] |  |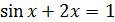
[0;1] |
Источник: studopedia.su
Решить в паскале
№1
Составить программу вычисления значений функции F(x) на отрезке [a;b] с шагом h. Результат представить в виде таблицы, первый столбец которой – значение аргумента, второй – соответствующие значения функции: F(x)=2cosx-1
№2
Дан числовой ряд и малая величина ?. Найти сумму ряда с точностью ?, общий член задан формулой: an=2n-1/2^n
1)var
a,b,h:real;
begin
readln(a);
readln(b);
readln(h);
while a begin
writeln(a,’ ‘,2*cos(a)-1:8);
a+=h;
end
end.
2)var
eps,sum,current,n:real;
begin
readln(eps);
sum:=0;
n:=0;
repeat
current:=2*n-1/power(2,n);
n+=1;
sum+=current;
until current>eps;
writeln(sum);
end.
Оцени ответ
Не нашёл ответ?
Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Информатика.
Источник: uchiru.net
F x ctgx 1 блок схема
Здесь можно сконструировать онлайн блок схему. Для этого надо ввести код в поле ввода, приведенное ниже. Сразу описываются структурные блоки, а затем связи между ними. После ввода — нажать кнопку «Рисовать». Сейчас введен код примера блок-схемы, которую Вы видите ниже.
Airlines.push_back(«1.Айрофлот»);
Airlines.push_back(«2.Айрофлот»);
Airlines.push_back(«3.Айрофлот»);
do ans;
if (ans == ‘Y’ || ans == ‘y’) N;
std::cout > count;
for (auto i = tickets.begin(); i != tickets.end(); i++)
else if (ans != ‘N’ ans != ‘N’)
int main()
> a >> b >> c >> d >> n >> m;
int minutes_ab = minutes(a, b);
int minutes_cd = minutes(c, d);
int minutes_nm = minutes(n, m);
cout
#include
#include
using namespace std;
int main() mr[i][j]) 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x главной ветвью графика котангенса.
п.2. Свойства функции y=ctgx
1. Область определения (xnepi k) — множество действительных чисел, кроме точек, в которых (sinx=0) .
2. Функция не ограничена сверху и снизу. Область значений (yinmathbb )
3. Функция нечётная $$ ctg(-x)=-ctgx $$
4. Функция периодическая с периодом π $$ ctg(x+pi k)=ctgx $$
5. Функция стремится к (-infty) при приближении слева к точкам (x=pi k) .
Приближение к точке a слева записывается как (xrightarrow a-0) $$ lim_ ctgx=-infty $$ Функция стремится к (+infty) при приближении справа к точкам (x=pi k) .
Приближение к точке a справа записывается как (xrightarrow a+0) $$ lim_ ctgx=+infty $$ Нули функции (y_ =0) достигаются в точках (x_0=fracpi2+pi k)
6. Функция убывает на всей области определения.
7. Функция имеет разрывы в точках (x=pi k) , через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами ((pi k; pi+pi k)) функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=ctgx на заданном промежутке:
a) (left[frac ; piright)) $$ y_ =lim_ ctgx=-infty, y_ =ctgleft(frac right)=-frac > $$ б) (left(0; frac right]) $$ y_ =ctgleft(frac right)=1, y_ =lim_ ctgx=+infty $$ в) (left[frac ; frac right]) $$ y_ =ctgleft(frac right)=-1, y_ =ctgleft(frac right)=sqrt $$
Пример 2. Решите уравнение:
a) (ctgx=-sqrt )
Бесконечное множество решений: (x=frac +pi k, kinmathbb )
б) (ctgleft(x+fracpi2right)=0)
(x+fracpi2=fracpi2+pi k)
Бесконечное множество решений: (x=pi k, kinmathbb )
в) (ctg(2x)=1)
(2x=fracpi4+pi k)
Бесконечное множество решений: (x=frac +frac , kinmathbb )
Пример 3. Постройте графики функций: a) (y(x)=x^2-2tgxcdot ctgx)
 |
Произведение (tgxcdot ctgx=1). При этом ограничивается область определения функции (y(x)), т.к. (tgx) и (ctgx) имеют разрывы. Точки разрыва отмечены на числовой окружности: (xnefrac ). |
Получаем: $$ begin x^2-2\ xnefrac , kinmathbb end $$ Строим график параболы и выкалываем точки, не входящие в ОДЗ.
 |
Сумма (sin^2(tgx)+cos^2(tgx)=1). При этом ограничивается область определения функции (y(x)), т.к. (tgx) имеeт разрывы. Точки разрыва отмечены на числовой окружности: (xnefrac +pi k). |
Получаем: $$ begin 1-x\ xnefrac +pi k, kinmathbb end $$ Строим график прямой и выкалываем точки, не входящие в ОДЗ.
Изображение алгоритма в виде блок-схемы
Блок-схемой называется наглядное графическое изображение алгоритма.
В блок-схеме отдельные этапы алгоритма изображают при помощи различных геометрических фигур – блоков.
Последовательность выполнения этапов указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями.
Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала (конца) алгоритма
и список переменных вводимых (выводимых).
Блок решения (арифметический)
Надпись: операция или группа операций.
Надпись: логическое условие.
Это группа операторов, отделенных друг от друга точкой с запятой, начинающихся с открывающей фигурной скобки .
Транслятор воспринимает составной оператор как один оператор.
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.
Условный оператор, соответствующий приведенной блок-схеме, имеет вид:
Вычисляется выражение. Если оно не равно нулю, т.е. имеет значение true, выполняется оператор_1, в противном случае (выражение равно нулю, т.е. false) – оператор_2.
Если в зависимости от некоторого условия выполняется некоторое действие, а в противном случае ничего не происходит, то алгоритм имет вид:
Условный оператор в этом случаеимет конструкцию:
Эту запись можно назвать «пропуск оператора else».
Здесь оператор либо выполняется, либо пропускается, в зависимости от значения выражения.
Если в какой-либо ветви условного процесса требуется выполнить несколько операторов, следует использовать составной оператор.
Задача 2. Известны коэффициенты а, b и с квадратного уравнения ax2+bx+c=0. Вычислить корни квадратного уравнения.
Задача 2. Решить ax4+bx2+c=0 биквадратное уравнение (y=x2).
1. Вычисление дискриминанта уравнения d.
2. Если d ³ 0, определяются y1 и y2, а иначе корней нет.
3. Если y1, y20 , то корней нет.
4. Если y1, y2 ³0 , то вычисляются четыре корня по формулам и выводятся значения корней.
5. Если условия 3) и 4) не выполняются, то необходимо проверить знак y1. Если y1³0, то вычисляются два корня по формуле . Если же y2³0, то вычисляются два корня по формуле . Вычисленные значения корней выводятся.
Задача 3.Решить кубическое уравнение:
После деления на a уравнение (1) принимает канонический вид:
В уравнении (2) сделаем замену и получим приведенное уравнение (3)
Число действительных корней приведенного уравнения (3) зависит от знака дискриминанта :
Количество корней кубического уравнения
| Дискриминант | Кол-во действительных корней |
| D?0 | |
| D |
При положительном дискриминанте кубического уравнения (3) действительный корень вычисляется по формулам:
При отрицательном дискриминанте уравнение (3) имеет 3 действительных корня:
После расчета корней приведенного уравнения (3) по формулам (4) или (5) необходимо перейти к корням заданного кубического уравнения (1):
[1] Текстовые файлы, в которых содержится описание используемых в программе элементов.
[2] Служат для уточнения внутреннего представления и диапазона значений стандартных типов
[3] Поток – виртуальный канал связи, создаваемый в программе для передачи данных
Статьи к прочтению:
КИНОШНОЕ ИЗОБРАЖЕНИЕ — БЕЗ БЮДЖЕТА!
Похожие статьи:
Разработка алгоритмов для структурного программирования и их реализация ВВЕДЕНИЕ Современным пользователям и профессиональным программистам приходится…
Наименование Обозначение Функция Блок начало-конец(пуск-остановка) Элементотображает вход из внешней среды или выход из неё (наиболее частое применение?…
Источник: remnabor.net