Составить программу которая определяла бы вид треугольника

Записная книжка рассеянного [в пространстве и времени] программиста

Часть 2: Тестирование простого приложения (Тестирование ПО)

Оглавление

Первое приложение

Программа считывает три целочисленных значения из консоли. Эти значения интерпретируются как длины сторон треугольника. Программа выводит сообщение о том, каким является данный треугольник — разносторонним, равнобедренным или равносторонним.

Напишем, функцию, которая принимает на вход три стороны треугольника, которые заданы целыми числами и возвращает тип треугольника. Сохраним написанный код в файле triangle.php.

Функция достаточно тривиальна, поэтому мы не будем останавливаться на ее реализации. Нас будет интересовать, как найти в ней ошибки.

Для начала потребуется реализовать механизм, который позволит вводить данные с консоли и получать результат. Сохраним следующий код в файле main.php. Чуть позже вы поймете, почему мы используем разные файлы для самой функции и для кода, который обрабатывает пользовательский ввод.

3 13 Определить вид треугольника по его длинам

// здесь мы подключим ранее написанную функцию для определения типа треугольника require __DIR__ . DIRECTORY_SEPARATOR . ‘triangle.php’; function main() // проинициализируем переменные $a = $b = $c = 0; // получим длины сторон со стандартного ввода $num = fscanf(STDIN, «%d %d %dn», $a, $b, $c); // если мы смогли считать длины трех сторон, // то вызовем нашу функцию и покажем результат if ($num == 3) switch (triangle_type($a, $b, $c)) case TRIANGLE_BAD: echo «Это не треугольникn»; break; case TRIANGLE_EQUILATERAL: echo «Это равносторонний треугольникn»; break; case TRIANGLE_ISOSCELES: echo «Это равнобедренный треугольникn»; break; case TRIANGLE_RIGHT: echo «Это прямоугольный треугольникn»; break; case TRIANGLE_SIDED: echo «Это разносторонний треугольникn»; break; > > > main();

Код также достаточно тривиален. Теперь мы можем запустить полученное приложение (да, это именно приложение — последовательность инструкций, определяющих процедуру решения конкретной задачи компьютером).

Откроем терминал, перейдем в каталог, с проектом и выполним следующую команду (для того, чтобы все сработало у вас должен быть установлен интерпретатор php в системе).

$ php main.php

Программа будет ожидать ввод трех чисел, разделенных пробелами.

И вот что мы можем увидеть на экране.

Поэкспериментируйте немного с программой вводя разные наборы чисел.

А теперь рассмотрим эту программу с точки зрения разработчика, которому досталось ее тестировать. Какие наборы тестов он должен разработать, чтобы отыскать все возможные баги? Прежде чем читать дальше подумайте и попробуйте посчитать то количество, которое придумали вы.

Итак. Ниже приведен набор тестовых сценариев, которые должны быть написаны для нашей функции.

1. тест для проверки действительно неравностороннего треугольника (наборы [1, 2, 3], [2, 5, 10] треугольниками не являются).
2. проверка на действительно равносторонний треугольник
3. проверка на равнобедренный треугольник (наборы вида [2, 2, 4] треугольником не являются)
4. как минимум три теста для проверки равнобедренного треугольника, которые представляют собой перестановки одного и того же набора чисел ([3, 3, 4], [3, 4, 3], [4, 3, 3])
5. тест на нулевую длину одной из сторон
6. тест на сторону, имеющую длину меньше нуля
7. проверка набора чисел, в котором сумма длин двух сторон равна третьей
8. тест перестановок для троек чисел из теста 7
9. проверка набора чисел, в котором сумма длин двух сторон меньше третьей ([12, 15, 30])
10. тест перестановок для троек чисел из теста 9
11. проверка на нулевую длину всех трех сторон
12. проверка на передачу нецелочисленных значений
13. проверка на передачу неполного набора значений
14. проверка не только входных данных, но и ожидаемого выходного значения в каждом из тестов 1-13

Если вы не смогли назвать все кейсы, то не пугайтесь. Среднее число тестов, которые называли в разное время опытные разработчики составило 7,8.

Что такое угол? Виды углов: прямой, острый, тупой, развернутый угол

Конечно нет никаких гарантий того, что набор тестов, удовлетворяющих перечисленным условиям, обнаружит все возможные ошибки. Но поскольку случаи 1-13 представляют ошибки, реально встречающиеся в различных версиях данной программы, адекватное тестирование должно обнаружить хотя бы их.

Это упражнение должно было продемонстрировать вам, что тестирование простых программ наподобие вышеприведенной является отнюдь не тривиальной задачей. А теперь попытайтесь представить себе, насколько трудоемким окажется тестирование, скажем, бухгалтерской программы крупного предприятия, компилятора или же системы управления воздушным движением, объем кода которых может достигать сотен тысяч строк. Еще большие трудности возникают с приложениями, которые написаны с использованием объектно-ориентированных языков (куда входит и php) и подходов. В частности, тесты для подобных приложений должны выявлять ошибки с созданием экземпляров объектов и взаимодействия между ними.

Однако, какой бы устрашающей ни казалась задача, адекватное (достаточно полное) тестирование программ является ключевой и, как вы убедитесь далее, вполне реализуемой частью процесса разработки программного обеспечения.

Тестируем

Конечно же самым простым решением будет просто закодировать все тестовые случаи для нашего проекта и написать нечто вроде следующего кода (файл triangle_test_simple.php).

require __DIR__ . DIRECTORY_SEPARATOR . ‘triangle.php’; function testForIsoscelesTriangle() echo «Test for [3, 4, 4]: «; if (triangle_type(3, 4, 4) == TRIANGLE_ISOSCELES) echo «okn»; > else echo «failn»; > > function main() testForIsoscelesTriangle(); > main();

И такое часто практикуется. Особенно в среде разработчиков на CC++. На каждый логически связанный набор тестовых случаев создается свой файл. Который содержит множество функций обрабатывающих по одному сценарию каждая.

В этом нет ничего плохого. Единственный минус такого подхода — отсутствие готового инструментария, который реализует все необходимые операции по обслуживанию и запуску тестов. Весь инструментарий приходится для каждого проекта реализовывать заново. Либо изготавливать свою собственную обвязку, которая будет кочевать из проекта в проект.

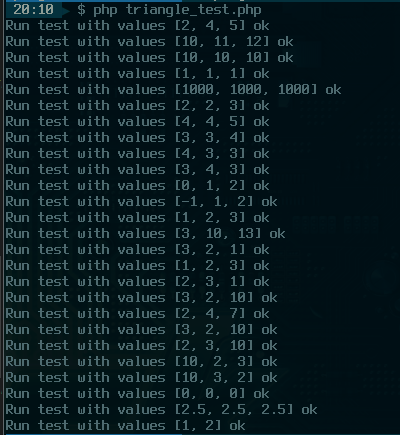
Один из вариантов создания инструмента для работы с подобными тестами вы можете увидеть в файле triangle_test.php. Запустите его и увидите на экране подробный лог тестирования проекта.

Литература

• “Искусство тестирования программ” Гленфорд Майерс, Том Баджетт, Кори Сандлер, ISBN: 978-5-8459-1974-8
• “PHP 7” Дмитрий Котеров, Игорь Симдянов, ISBN 978-5-9775-3725-4

Исходные тексты программ

Оглавление

RSS feed This page was generated by GitHub Pages.

Источник: russianpenguin.ru

Условный оператор. Функции.

Для ввода данных, вычислений и вывода данных использовать отдельные функции (методы). Не использовать глобальные переменные, все необходимые данные передавать в эти функции (методы).

Звездочками отмечены достаточно сложные задачи.

1. Для точки на плоскости определить, какой координатной плоскости принадлежит данная точка.

2. Даны координаты трех точек на плоскости. Составить программу, которая определяла бы вид треугольника (равносторонний, равнобедренный, разносторонний, прямоугольный, тупоугольный, остроугольный), если данные координаты вершин позволяют его построить.

3. (*) Даны координаты трех вершин прямоугольника. Определить координаты четвертой вершины. Стороны прямоугольника не обязательно параллельны осям координат. Три вершины могут задаваться в произвольном порядке.

4. Даны координаты 4-х точек, определить, могут ли они быть вершинами квадрата.

5. Даны две прямые, заданные уравнением ax+by+c=0. Определить взаимное расположение прямых (совпадают, параллельны, пересекаются) и, если прямые пересекаются, точку пересечения прямых.

6. Решить квадратное уравнение.

7. Нагревают m литров воды, начальная температура воды t. Воде было передано k джоулей энергии. Определить, сколько воды осталось и какой температуры (варианты: вода нагрелась до температуры менее 100 градусов, температура нагрелась до 100 градусов и часть воды испарилась, вся вода испарилась). Коэффициенты физических процессов взять из школьного курса физики.

8. Написать программу перевода обычных координат в полярные координаты (на плоскости). Проверить корректность программы для точек во всех координатных четвертях.

9. Проверить, можно ли вписать в треугольник со сторонами A, B, C круг с радиусом R (заодно проверить возможность существования треугольника).

10. Проверить можно ли вписать в прямоугольный треугольник с гипотенузой С круг с радиусом R (заодно проверить возможность существования треугольника).

11. Даны две окружности, заданные в виде координат центра (X, Y) и радиуса R. Проверить их взаимное расположение (варианты: пересекаются в 2-х точках, касаются (1 общая точка) с внешней стороны, касаются (1 общая точка) с внутренней стороны, не пересекаются не вписаны одна в другую, не пересекаются одна окружность вписана в другую). При сравнении на равенство вещественных чисел использовать сравнение с заданной точностью (e – константа).

12. (*) Даны три вершины треугольника. Узнать, в каких четвертях (на координатной сетке) он находится. Координаты треугольника ((X1, Y1), (X2, Y2), (X3, Y3)) задаются в произвольном порядке. Учесть, что треугольник вида ((-1, -1), (-1, 5), (5, -1)) лежит сразу в 4-х плоскостях. Распечатать четверти, в которых лежит треугольник, в виде цифр через запятую в порядке от 1 до 4, например, для приведенного выше треугольника вывод будет выглядеть так: 1, 2, 3, 4.

13. Проверить, пройдет ли кирпич в прямой отверстие. Размеры кирпича — A, B, C (длина, высота, ширина — задаются в произвольном порядке). Размеры отверстия W, H (ширина, высота — задаются в произвольном порядке). Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.

14. Даны три числа A, B, C (в произвольном порядке). Проверить, можно ли из этих чисел составить арифметическую или геометрическую прогрессию. Если да, то распечатать параметры этой прогрессии.

15. (*) У вас есть 4 круга радиуса R и квадрат со стороной A. Проверить, можно ли полностью закрыть квадрат этими кругами, размещая круги в любом положении над квадратом. Если закрыть квадрат 4-ми кругами возможно, найти минимальное кол-во кругов, которые для этого потребуются.

16. (*) По заданным двум клеткам на шахматной доске, определить (и напечатать), какие белые фигуры могут совершить ход из первой клетки во вторую. Клетки задаются в шахматной нотации, например d1 и b3 (из первой во вторую может пойти ферзь и слон). Для каждой фигуры написать функцию, проверяющую возможность хода данной фигурой. (Предполагается, что на шахматной доске нет других фигур, которые могу помешать совершить ход нужной фигурой.)

18. Дан номер некоторого года (положительное целое число). Вывести число дней в этом году, учитывая, что обычный год насчитывает 365 дней, а високосный — 366 дней. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400 (например, годы 300, 1300 и 1900 не являются високосными, а 1200 и 2000 — являются).

20. Мастям игральных карт присвоены порядковые номера: 1 — пики, 2 — трефы, 3 — бубны, 4 — червы. Достоинству карт, старших десятки, присвоены номера: 11 — валет, 12 — дама, 13 — король, 14 — туз. Даны два целых числа: N — достоинство (6 ≤ N ≤ 14) и M — масть карты (1 ≤ M ≤ 4). Вывести название соответствующей карты вида «шестерка бубен», «дама червей», «туз треф» и т.п.

Для формирования названия карты реализовать функцию.

21. (*) Дано целое число в диапазоне 1–99, определяющее возраст (в годах). Вывести строку-описание указанного возраста, обеспечив правильное согласование числа со словом «год», например: 3 — «3 года», 20 — «двадцать лет», 32 — «тридцать два года», 41 — «сорок один год». Для формирования возраста в виде строки реализовать функцию.

23. Вам известен какой-то день в текущем года (задается в виде 2-х чисел — дата и номер месяца). Определить, будет ли заданный день рабочим или выходным днем с учетом праздников и переносом рабочих и выходных дней (можно посмотреть, например, здесь: https://calendar.yuretz.ru/). Реализовать в виде функции.

24. (*) Определить, можно ли коробку со сторонами A1, B1, C1 поместить в другую коробку со сторонами A2, B2, C2 или наоборот (т.е. поместить вторую коробку в первую). Для того, чтобы одну коробку можно было поместить в другую, каждая из соответствующих сторон одной коробки должна быть строго меньше сторон другой коробки. Стороны коробок задаются в произвольном порядке.

При размещении коробок одна в другую коробки можно произвольным образом вращать. Реализовать функцию проверки возможности размещения одной коробки в другой. Распечатать ответ вида «Первая коробка помещается во второй», «Вторая коробка помещается в первой» или «Коробки нельзя разместить одна в другой». Совет: прежде чем сравнивать стороны, их необходимо упорядочить.

25. Только что закончился футбольный матч со счетом N:M. Определить, сколько очков заработала каждая команда, если за победу дается 3 очка, за ничью — 1, за проигрыш — 0.

26. Известны результаты 2-х футбольных матчей между 2-мя командами N1:M1 и N2:M2 (команды одни и те же, просто первый матч был на домашнем поле первой команды, а второй — на домашнем поле второй команды). В следующий круг соревнований выходит команда, которая забила больше мячей, чем пропустила. Если же количество забитых и пропущенных мячей одинаково — то команда, которая забила больше мячей на чужом поле (одна команда обязательно по разнице забитых и пропущенных мячей должна быть лучшей хотя бы по послематчевым пенальти, которые учитываются в счете второго матча). Определить, какая их двух команд выходит в следующий круг соревнований.

27. (*) Даны 4-ре координаты вершин четырехугольника. Проверить, образует ли данный четырехугольник параллелограмм. Совет: реализовать вспомогательную функцию проверки параллельности 2-х отрезков.

28. В магазине продаются торты 2-х видов. Цена первого торта P1, в наличии N1 торта такого вида. Цена второго торта P2, в наличии N2 торта такого вида. Какое максимальное кол-во тортов можно купить в данном магазине располагая суммой в M денег.

29. Задача соответствует предыдущей, однако есть дополнительное условие. Обязательно необходимо купить разные торты (т.е. хотя бы один торт каждого вида). Если такое невозможно, торты вообще не покупать.

30. В классе N мальчиков и M девочек. Необходимо разбить всех учеников на команды так, чтобы в каждой команде было ровно по 3 человека (и мальчики и девочки). Необходимо определить, какое максимальное кол-во команд, следуя данным правилам, можно составить из учеников данного класса. (Очевидно, что возможны ситуации, когда некоторые ученики не войдут ни в одну команду.)

Источник: poisk-ru.ru