надо написать программу Построить интерполяционный многочлен Лагранжа по известным в узлах x0,x1. x5, значения функции f(x). Вычислить значения этого многочлена в равномерной сетке точек на отрезке [a,b] с шагом h и сравнить их со значениями функции f(x) в этих точках f(x)= 4^cos(x) x0=0.6 x1=0.8 x2=0.9 x3=1.0 x4=1.3 x5=1.4 a=0.5 b=1.5 h=0.02 пока вот что есть
program mnogoch; Var x,x0,x1,x2,x3,x4,a,b,h,y,f0,f1,f2,f3,f4,fx:Real; Function f(x:real):real; Begin f:=exp(ln(4)*cos(x)); end; a:=0.5; b:=1.5; h:=0.02 x0:=0.6; x1:=0.8; x2:=0.9; x3:=1.0; x4:=1.3; x5:=1.4; x:=a; repeat y:=exp(ln(4)*cos)); f0:=f(x0)*(x-x1)*(x-x2)*(x-x3)*(x-x4)*(x-x5)/(x0-x1)*(x0-x2)*(x0-x3)*(x0-x4)*(x0-x5); f1:=f(x1)*(x-x0)*(x-x2)*(x-x3)*(x-x4)*(x-x5)/(x1-x0)*(x1-x2)*(x1-x3)*(x1-x4)*(x1-x5); f2:=f(x2)*(x-x0)*(x-x1)*(x-x3)*(x-x4)*(x-x5)/(x2-x0)*(x2-x1)*(x2-x3)*(x2-x4)*(x2-x5); f3:=f(x3)*(x-x0)*(x-x1)*(x-x2)*(x-x4)*(x-x5)/(x3-x0)*(x3-x1)*(x3-x2)*(x3-x4)*(x3-x5); p4:=f(x4)*(x-x0)*(x-x1)*(x-x2)*(x-x3)*(x-x5)/(x4-x0)*(x4-x1)*(x4-x2)*(x4-x3)*(x4-x5); fx:=f0+f1+f2+f3+f4; if px>y then begin writeln (‘p[‘,x:1:1,’]=’,px:10:10,’ > y[‘,x:1:1,’]=’,y:10:10); writeln end; if fxb; end.
все уже сделано и сдано
Алгоритмы. Интерполяционный полином Лагранжа.
Код к задаче: «Построить интерполяционный многочлен Лагранжа»
Листинг программы
Uses crt; Const nmax = 100; Var n,k,m,I,j : integer; ct,u:real; x,y,r,pt:array[1..nmax] of real; begin clrscr; repeat write(‘Число узлов интерполирования от 2 до ‘,nmax,’ n=’); readln(n); until n in [2..nmax]; writeln(‘Введите массив узлов интерполирования:’); for i:=1 to n do begin write(‘x[‘,i,’]=’); readln(x[i]); end; writeln(‘Введите массив значений функции в узлах:’); for i:=1 to n do begin write(‘y[‘,i,’]=’); readln(y[i]); end; clrscr; writeln(‘Массив узлов:’); for i:=1 to n do write(x[i]:6:4,’ ‘); writeln; writeln; writeln(‘Массив значений:’); for i:=1 to n do write(y[i]:6:4,’ ‘); writeln; writeln; for i:=1 to n do R[i]:=0; for i:=1 to n do begin ct:=1;pt[1]:=1;k:=1; for j:=1 to n do if i<>j then begin ct:=ct*(x[i]-x[j]); pt[k+1]:=1; if k>1 then for m:=k downto 2 do pt[m]:=pt[m-1]-pt[m]*x[j]; pt[1]:=-pt[1]*x[j]; k:=k+1; end; u:=y[i]/ct; for m:=1 to n do r[m]:=r[m]+pt[m]*u; end; writeln(‘Массив коэффициентов:’); for i:=1 to n do write(‘R[‘, i, ‘]=’, r[i]:6:4,’ ‘); readln end.
Источник: studassistent.ru
Вариант 25
Теоретическая часть Интерполяция, полином Лагранжа Общие положения.
В вычислительной практике часто приходится иметь дело с функциями , заданными таблицами их значений для некоторого конечного множества значений х: .
В процессе же решения задачи необходимо использовать значения для промежуточных значений аргумента. В этом случае строят функцию Ф(x), достаточно простую для вычислений, которая в заданных точках x0, x1. xn, называемых узлами интерполяции, принимает значения , а в остальных точках отрезка (x0,xn), принадлежащего области определения , приближенно представляет функцию с той или иной степенью точности.
Полином Лагранжа (интерполяционный полином Лагранжа)
При решении задачи в этом случае вместо функции оперируют с функцией Ф(x). Задача построения такой функции Ф(x) называется задачей интерполирования. Чаще всего интерполирующую функцию Ф(x) отыскивают в виде алгебраического полинома.
Интерполяционный полином.
Для каждой функции , определенной на [a,b], и любого набора узлов x0, x1. xn( xi [a,b], xi xj при i j ) среди алгебраических многочленов степени не выше n существует единственный интерполяционный многочлен Ф(x), который может быть записан в форме:
где — многочлен n-ой степени, обладающий следующим свойством:
Для интерполяционного полинома многочлен имеет вид:
Этот многочлен (1) и решает задачу интерполирования и называется интерполяционным полиномом Лагранжа.
В качестве примера рассмотрим функцию вида на интервале заданную табличным способом.
Необходимо определить значение функции в точке x-2.5. Воспользуемся для этого полином Лагранжа. Исходя из формул (1 и 3) запишем этот полином в явном виде:
Тогда подставляя в формулу (4) исходные значения из нашей таблицы получим
Полученный результат соответствует теории т.е. .
Интерполяционная формула Лагранжа
Интерполяционный полином Лагранжа может быть записан в другой форме:
Запись полинома в виде (5) более удобна для программирования.
При решении задачи интерполяции величина n называется порядком интерполирующего полинома. При этом, как видно из формул (1) и (5), число узлов интерполирования всегда будет равно n+1 и значение x, для которого определяется величина , должно лежать внутри области определения узлов интерполяции т.е.
В некоторых практических случаях общее известное число узлов интерполяции m может быть больше, чем порядок интерполирующего полинома n.
В этом случае, прежде чем реализовывать процедуру интерполяции согласно формуле (5), необходимо определить те узлы интерполяции, для которых справедливо условие (6). При этом следует помнить, что наименьшая погрешность достигается при нахождении значения x в центре области интерполяции. Для обеспечения этого предлагается следующая процедура:
- После ввода в программу значения величины х необходимо проверить условие x0 x xm, где x0и xm – начальное и конечное значение узловых точек интерполяции.
- При выполнения предыдущего условия начинается поиск области интерполяции, для чего находим первоеxi такое, для которого выполняется условие xi >x, при этом номер i будет соответствовать середине интервала интерполяции. Для определения области интерполяции ее левая граница будет начинаться с номера , а заканчиваться узлом с номером .
- После выполнения пунктов 1 и 2 программируется формула (5).
Основное назначение интерполяции – это вычисление значений табулированной функции для неузловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют «искусством чтения таблиц между строками».
Описание алгоритма решения задачи
- Программа запрашивает порядок полинома, х, количество точек, проверяя с помощью цикла do while соответствие с заданием. Если порядок полинома+1 больше, чем количество точек, то порядок уменьшается до максимально возможного.
- С помощью цикла в массив с двумя столбцами записываются значения
- В файл сразу записываются значения, введенные с клавиатуры
- Так как предполагается, что аргументы изначально упорядочены по возрастанию, поэтому выполняется проверка на то, чтобы искомый аргумент заключался между крайними.
- Далее в случае, если порядок полинома+1 меньше, чем количество точек, то стартует цикл, выбирающий границы подсчета х в соответствии с порядком полинома.
- Начинается вычисление значения значение функции от заданного х в соответствии с вышеуказанной формулой
- Результат записывается в файл, после чего пользователю предлагается еще раз повторить процедуру.
Руководство программиста
Программный код приложения разрабатывался на языке СИ.
Блок-схема алгоритма программы приведена в приложении А.
Листинг программы приведен в приложении В.
Пример входного и выходного файла в приложении С.
Руководство пользователя
В каталоге с приложением должен находиться текстовой файл table.txt, в первом столбце которого находятся аргументы, а во втором соответствующие значения функции. Для корректной работы программы аргументы должны идти строго по возрастанию. Максимальное число строк-120. После запуска программа потребует значение аргумента, порядок полинома и количество считываемых точек. Не имеет смысла задавать порядок полинома больше, чем количество точек+1, а так же аргумент должен лежать в пределах определения функции. Процедуру можно повторять сколько угодно раз, после чего посмотреть результаты в файле FX.txt
Вывод: В ходе лабораторной работы был изучен метод восстановления функциональных зависимостей – интерполяция, а так же данный метод реализован программно на языке СИ
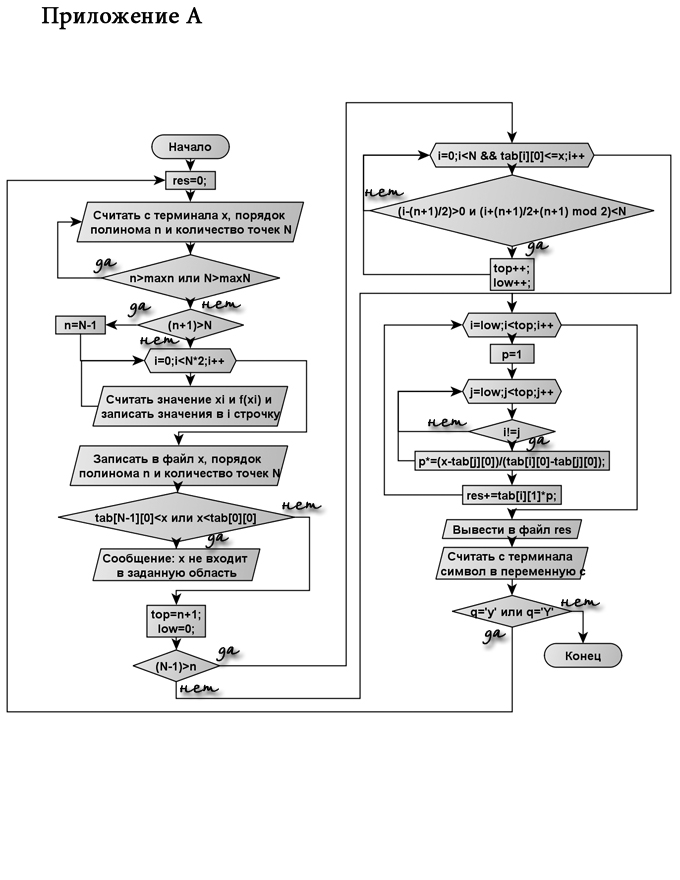
Приложение В
Источник: studfile.net
Составить программу интерполирования функции с использованием полинома лагранжа
Прошу помочь с написание программы по приложенной блок-схеме.
То,что есть у меня::confused:
——————————-
Uses crt; Const nmax = 10; Type R = array [1..nmax] of real; Var n ,x,y,ct,Pt,k,m,I,j : integer; begin clrscr; R[i]:=0; write (‘vvedite n = ‘); read(n); writeln(‘vvedite element massiva’); for i:=1 to n do for j:=1 to n do read(х[i,j]); writeln(‘enter massive Y’); for i:=1 to n do begin ct:=1; Pt[i]:=1; k:=1; end; for i:=1 to n do if i <>j then begin ct:=ct*(x[i]-x[j]); Pt[k+1]:=1; If k>1 then for m :=k down to 2 Pt[m]:=Pt[m-1] – Pt[m]*x[j] else Pt[1]:=-Pt[1]*x[j]; K:=k+1; End; u := y[i]/ct; for m:=1 to n do R[m]=R[m] + Pt[m]*n End; end; end; For i:=1 to n do Write(R[i]:8:2); End; readkey End.
——————————-
Я к программированию не буду иметь никакого отношения после того,как сдам наконец эту программу.
Буду благодарна,если подскажите..
Последний раз редактировалось Stilet; 02.06.2010 в 10:35 .
Регистрация: 01.06.2010
Сообщений: 5
C программой мне помогли:
Uses crt; Const nmax = 100; Var n,k,m,I,j : integer; ct,u:real; x,y,r,pt:array[1..nmax] of real; begin clrscr; repeat write(‘Число узлов интерполирования от 2 до ‘,nmax,’ n=’); readln(n); until n in [2..nmax]; writeln(‘Введите массив узлов интерполирования:’); for i:=1 to n do begin write(‘x[‘,i,’]=’); readln(x[i]); end; writeln(‘Введите массив значений функции в узлах:’); for i:=1 to n do begin write(‘y[‘,i,’]=’); readln(y[i]); end; clrscr; writeln(‘Массив узлов:’); for i:=1 to n do write(x[i]:0:2,’ ‘); writeln; writeln; writeln(‘Массив значений:’); for i:=1 to n do write(y[i]:0:2,’ ‘); writeln; writeln; for i:=1 to n do R[i]:=0; for i:=1 to n do begin ct:=1;pt[1]:=1;k:=1; for j:=1 to n do if i<>j then begin ct:=ct*(x[i]-x[j]); pt[k+1]:=1; if k>1 then for m:=k downto 2 do pt[m]:=pt[m-1]-pt[m]*x[j]; pt[1]:=-pt[1]*x[j]; k:=k+1; end; u:=y[i]/ct; for m:=1 to n do r[m]:=r[m]+pt[m]*u; end; writeln(‘Массив коэффициентов:’); for i:=1 to n do write(r[i]:0:2,’ ‘); readln end.
Подскажите, как избавиться от ошибки «деление на ноль»(вылезает,когда вводишь данные)?
Пользователь
Регистрация: 22.01.2010
Сообщений: 37
Лагранж
Насколько я знаю, задается кол-во узлов интерполяции, массив узлов интерполяции и массив значений в узлах интерполяции. В знаменателях многочлена, как правило, нулей не бывает. Для тестирования проверьте нижеприведённую программу.
Она была составлена для Дельфи, но вы сможете переделать её для Паскаля. Проверьте её с вашими данными
Регистрация: 01.06.2010
Сообщений: 5
Программа нормально заработала, выводит эти коэффициенты.
пошла сдавать программу — препод не принял Сказал, что программа должна выводить коэффициенты в порядке возрастания, у меня просто вразброс выводит..
Что нужно исправить или дописать?Подскажите,пожалуйста
Пользователь
Регистрация: 22.01.2010
Сообщений: 37
полином Лагранжа
Добавьте переменную Kf: real;
#
L:=0;
for i:=0 to n-1 do
begin
p1:=1;
p2:=1;
for j:=0 to n-1 do
begin
if i<>j then
begin
p1:=p1*(xx-x[j]);
p2:=p2*(x[i]-x[j]);
end;
// Это добавьте
Kf:=y[i]*p1/p2;
writeln(Kf:6:4);
end;
L:=L+Kf;
end;
writeln(L:6:4);
#
Последний раз редактировалось Fuadik; 05.06.2010 в 19:30 . Причина: моя ошибка
Регистрация: 01.06.2010
Сообщений: 5
Fuadik,
Большое Спасибо!)
А скажите, в каком виде должна мне ответ выводить программа, если в таблице ответов есть вот что.
В таблице t1,t2,t3,t4 – это числитель коэффициентов, а с1,с2,с3,с4 – это yi/знаменатель коэффициентов. эта таблица как раз для моих значений(х1=-1, х2=0, х3=1, х4=2 y1=-2, y2=1, y3=2, y4=1)
под блок-схемой написано, что массив должен выводиться в порядке возрастания степени (n-1 )-я так понимаю, это ж степень при х?
значит моя программа должна выдавать массив: 1 2 -1 0 ??
или я что-то не так понимаю?
Изображения
| ОТВЕТЫ.jpg (43.6 Кб, 476 просмотров) |
Пользователь
Регистрация: 22.01.2010
Сообщений: 37
Лагранж
Программа, с которой вам помогли, нормально работает. Проверьте вашу программу. У вас в выводе данных под целую часть было указано 0, а под дробную часть 2. Я поменял на 6:4.
Uses crt; Const nmax = 100; Var n,k,m,I,j : integer; ct,u:real; x,y,r,pt:array[1..nmax] of real; begin clrscr; repeat write(‘Число узлов интерполирования от 2 до ‘,nmax,’ n=’); readln(n); until n in [2..nmax]; writeln(‘Введите массив узлов интерполирования:’); for i:=1 to n do begin write(‘x[‘,i,’]=’); readln(x[i]); end; writeln(‘Введите массив значений функции в узлах:’); for i:=1 to n do begin write(‘y[‘,i,’]=’); readln(y[i]); end; clrscr; writeln(‘Массив узлов:’); for i:=1 to n do write(x[i]:6:4,’ ‘); writeln; writeln; writeln(‘Массив значений:’); for i:=1 to n do write(y[i]:6:4,’ ‘); writeln; writeln; for i:=1 to n do R[i]:=0; for i:=1 to n do begin ct:=1;pt[1]:=1;k:=1; for j:=1 to n do if i<>j then begin ct:=ct*(x[i]-x[j]); pt[k+1]:=1; if k>1 then for m:=k downto 2 do pt[m]:=pt[m-1]-pt[m]*x[j]; pt[1]:=-pt[1]*x[j]; k:=k+1; end; u:=y[i]/ct; for m:=1 to n do r[m]:=r[m]+pt[m]*u; end; writeln(‘Массив коэффициентов:’); for i:=1 to n do write(‘R[‘, i, ‘]=’, r[i]:6:4,’ ‘); readln end.
___________
Код нужно оформлять по правилам:
тегом [CODE]..[/СODE]
(это кнопочка на панели форматирования с решёточкой #)
Не забывайте об этом!
Последний раз редактировалось Serge_Bliznykov; 15.10.2013 в 15:31 .
Источник: www.programmersforum.ru