Пример №3. Решение задачи линейного программирования симплекс методом.
Нахождение наибольшего значения функции (искусственный базис)
Данное решение сделано калькулятором, представленным на сайте.
Найти наибольшее значение функции
| F | = | — | x1 | + | 3 | x2 |
при следующих ограничениях:
| x1 | + | 2 | x2 | ≤ | 4 | |
| x1 | — | x2 | ≥ | 1 | ||
| x1 | + | x2 | ≤ | 8 |
x1 ≥ 0 x2 ≥ 0
1. Свободные члены системы должны быть неотрицательными.
Данное условие выполнено.
2. Каждое ограничение системы должно представлять собой уравнение.
| x1 | + | 2 | x2 | ≤ | 4 | |
| x1 | — | x2 | ≥ | 1 | ||
| x1 | + | x2 | ≤ | 8 |
| x1 | + | 2 | x2 | + | S1 | = | 4 | |
| x1 | — | x2 | — | S2 | = | 1 | ||
| x1 | + | x2 | + | S3 | = | 8 |
S1 ≥ 0, S2 ≥ 0, S3 ≥ 0. Введенные переменные S1, S2, S3, называются балансовыми переменными.
Урок 3. Решение задачи симплекс-методом. Для тех, кто не разобрался с алгоритмом симплекс-метода.
3. Нахождение начального базиса и значения функции F, которое соответствует найденному начальному базису.
Что такое базис?
Переменная называется базисной для данного уравнения, если она входит в данное уравнение с коэффициентом один и не входит в оставшиеся уравнения системы (при условии, что в правой части уравнения стоит неотрицательное число).
Если в каждом уравнении присутствует базисная переменная, тогда говорят, что в системе присутствует базис.
Переменные, которые не являются базисными, называются свободными.
В чем заключается идея симплекс метода?
Каждому базису соответствует единственное значение функции. Одно из них является наибольшим значением функции F.
Мы будем переходить от одного базиса к другому.
Следующий базис будем выбирать таким образом, чтобы получить значение функции F не меньше имеющегося.
Очевидно, количество возможных базисов для любой задачи число не очень большое.
Следовательно, рано или поздно, ответ будет получен.
Как осуществляется переход от одного базиса к другому?
Запись решения удобнее вести в виде таблиц. Каждая строка таблицы эквивалентна уравнению системы. Выделенная строка состоит из коэффициентов функции (см. таблицу ниже). Это позволяет не переписывать переменные каждый раз, что существенно экономит время.
B выделенной строке выбираем наибольший положительный коэффициент (можно выбрать любой положительный).
Cимплексный метод решения задачи линейного программирования (ЗЛП)
Это необходимо для того, чтобы получить значение функции F не меньше имеющегося.
Выбран столбец.
Для положительных коэффициентов выбранного столбца считаем отношение Θ и выбираем наименьшее значение.
Это необходимо для того, чтобы после преобразования столбец свободных членов остался неотрицательным.
Выбрана строка.
Определен элемент, который будет базисным. Далее считаем.
В нашей системе есть базис?
| x1 | + | 2 | x2 | + | S1 | = | 4 | |
| x1 | — | x2 | — | S2 | = | 1 | ||
| x1 | + | x2 | + | S3 | = | 8 |
Базиса нет, т.е. мы не можем начать решение.
Придется его найти. Для этого решим вспомогательную задачу.
Добавим искусственную переменную в то уравнение, где нет базисной переменной.
| x1 | + | 2 | x2 | + | S1 | = | 4 | |
| x1 | — | x2 | — | S2 | + | R1 | = | 1 |
| x1 | + | x2 | + | S3 | = | 8 |
R1 ≥ 0. Введенная переменная R1, называется искусственной переменной.
Введем в рассмотрение функцию W и будем искать ее наименьшее значение.
Алгоритм нахождения наименьшего значения функции W имеет только одно отличие от алгоритма, рассмотренного выше.
Приравниваем свободные переменные нулю. Устно находим значения базисных переменных. (см. систему)
Функция W выражена через свободные переменные. Поэтому значение функции W, для данного базиса, можно найти мгновенно.
| x1 = 0 x2 = 0 S2 = 0 S1 = 4 S3 = 8 R1 = 1 |
=> W = 1 |
| x1 | x2 | S1 | S2 | S3 | R1 | св. член | Θ |
| 1 | 2 | 1 | 4 | 4 : 1 = 4 | |||
| 1 | -1 | -1 | 1 | 1 | 1 : 1 = 1 | ||
| 1 | 1 | 1 | 8 | 8 : 1 = 8 | |||
| -1 | 1 | 1 | W — 1 | ||||
| 3 | 1 | 1 | -1 | 3 | |||
| 1 | -1 | -1 | 1 | 1 | |||
| 2 | 1 | 1 | -1 | 7 | |||
| 1 | W — 0 |
Приравниваем свободные переменные нулю. Устно находим значения базисных переменных. (см. таблицу)
Функция W выражена через свободные переменные. Поэтому значение функции W, для данного базиса, можно найти мгновенно. (см. выделенную строку таблицы)
| x2 = 0 S2 = 0 R1 = 0 x1 = 1 S1 = 3 S3 = 7 |
=> W — 0 = 0 => W = 0 |
Среди коэффициентов выделенной строки нет отрицательных. Следовательно, найдено наименьшее значение функции W.
Получен базис без использования искусственной переменной. Что и требовалось.
Столбец, соответствующий искусственной переменной можно вычеркнуть.
В итоге, наша система выглядит следующим образом:
Приравниваем свободные переменные нулю. Устно находим значения базисных переменных. (см. систему)
Функция F выражена через свободные переменные. Поэтому значение функции F, для данного базиса, можно найти мгновенно.
| x2 = 0 S2 = 0 x1 = 1 S1 = 3 S3 = 7 |
=> F = -1 |
Начальный базис найден и получено значение функции F, соответствующее найденному базису.
4. Нахождение наибольшего значения функции F.
| x1 | x2 | S1 | S2 | S3 | св. член | Θ |
| 3 | 1 | 1 | 3 | 3 : 3 = 1 | ||
| 1 | -1 | -1 | 1 | |||
| 2 | 1 | 1 | 7 | 7 : 2 = 3,5 | ||
| 2 | -1 | F + 1 | ||||
| 1 | 1/3 | 1/3 | 1 | |||
| 1 | -1 | -1 | 1 | |||
| 2 | 1 | 1 | 7 | |||
| 2 | -1 | F + 1 | ||||
| 1 | 1/3 | 1/3 | 1 | |||
| 1 | 1/3 | -2/3 | 2 | |||
| -2/3 | 1/3 | 1 | 5 | |||
| -2/3 | -5/3 | F — 1 |
Приравниваем свободные переменные нулю. Устно находим значения базисных переменных. (см. таблицу)
Функция F выражена через свободные переменные. Поэтому значение функции F, для данного базиса, можно найти мгновенно. (см. выделенную строку таблицы)
| S1 = 0 S2 = 0 x1 = 2 x2 = 1 S3 = 5 |
=> F — 1 = 0 => F = 1 |
Среди коэффициентов выделенной строки нет положительных. Следовательно, найдено наибольшее значение функции F.
Источник: reshmat.ru
Решение задачи линейного программирование симплекс-методом — PascalABC.NET
Разработайте алгоритм реализации симплексного метода линейного программирования.Оформите этот алгоритм с использованием процедур (или функции). Затраты сырья на единицу изделия A: Затраты сырья на единицу изделия B: Количество имеющегося сырья: Прибыль от реализации ед. продукции:
Код к задаче: «Решение задачи линейного программирование симплекс-методом»
Листинг программы
program zl; const n=3; m=2; n1=3; var str:array[1..m]of integer; a,a1,a2:array[1..n,1..m]of real; b,b1,b2:array[1..n]of real; c,c1,c2,otvet:array[1..m]of real; k,x,i,j:integer; w:real; function res:real; var i,j:integer; r:real; begin r:=0; for j:=1 to m do if c1[j]=0 then for i:=1 to n1 do if a1[i,j]=1 then begin r:=r+c[j]*b1[i]; otvet[j]:=b1[i]; break; end; res:=r; end; function IA:integer; var min,max:real; i,j,stol:integer; begin max:=-maxint; for j:=1 to m do begin min:=maxint; for i:=1 to m do if a1[i,j]<>0 then if abs(b1[i]/a1[i,j])max then begin max:=c1[j]*min; stol:=j; end; end; IA:=stol; end; function opt:boolean; var i:byte; t:boolean; begin t:=true; for i:=1 to m do if c1[i]>0 then t:=false; opt:=t; end; procedure gg; var i,j:integer; begin writeln; for i:=1 to n do begin for j:=1 to m do write(a1[i,j]:8:2); writeln(b1[i]:8:3); end; for i:=1 to m do write(c1[i]:8:2); end; begin a[1,1]:=15; a[1,2]:=2; b[1]:=300; a[2,1]:=12; a[2,2]:=6; b[2]:=306; a[3,1]:=3; a[3,2]:=12; b[3]:=360; c[1]:=9; c[2]:=6; a1:=a; b1:=b; c1:=c; k:=0; while not(opt) do begin a2:=a1; b2:=b1; c2:=c1; x:=IA; k:=k+1; w:=a1[str[x],x]; gg; writeln; for i:=1 to m do a1[str[x],i]:=a2[str[x],i]/w; b1[str[x]]:=b2[str[x]]/w; for i:=1 to n do if str[x]<>i then begin for j:=1 to m do a1[i,j]:=a2[i,j]-a1[str[x],j]*a2[i,x]; b1[i]:=b2[i]-b1[str[x]]*a2[i,x]; for j:=1 to m do c1[j]:=c2[j]-a1[str[x],j]*c2[x]; end; end; gg; writeln; writeln(‘optim result=’,res:10:10); write(‘vector reshenuya=’); for i:=1 to m do write(otvet[i]:8:3); readln; readln; end.
Источник: studassistent.ru
Лабораторная работа № 2 Решение задач линейного программирования симплекс-методом
Программа для решения задач линейного программирования симплекс-методом. Имеется три режима решения задач:
В первом режиме программа сама выбирает разрешающий столбец и строку, которые обеспечивают максимальное возрастание или уменьшение целевой функции. А также автоматически пересчитывает все таблицы.
В пошаговом режиме, каждая пересчитанная таблица выводится на экран. Этот режим удобен для просмотра промежуточных результатов решения задачи. Разрешающий столбец и строку, в данном режиме, программа также выбирает сама.
В ручном режиме пользователь сам выбирает разрешающую строку и столбец.
Также есть возможность экспорта всех таблиц, полученных в ходе решения задачи, в Excel.
2) Интерфейс программы
Правило заполнения таблицы:
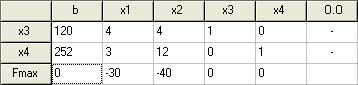
В первый столбец “b” вносятся свободные члены ограничений и целевой функции. В последнюю строку вносятся коэффициенты при целевой функции. В остальные ячейки вносятся коэффициенты при ограничениях.
Образец выполнения лабораторной работы
Пример задачи на максимизацию
Завод выпускает продукцию 1-го и 2-го типа. Прибыль от реализации единицы продукции соответственно составляет 30 и 40 у.е. На выпуск единицы продукции 1-го типа расходуется 4 единиц сырья категории А, 4 ед. – категории В. Для выпуска единицы продукции 2-го типа расходуется сырья категории А — 3 ед., категории С – 12 единицы. Имеющиеся в наличие запасы сырья категории А – 120 единиц, В – 252 единицы.
Тип выпускаемой продукции
Расход сырья (ед.)
Прибыль от реализации единицы продукции (у.е.)
Запасы сырья (ед.)
Необходимо определить количество продукции, при выпуске которой прибыль является максимальной.
Предположим, что будет изготовлено x1 единиц продукции 1-го типа, х2 – 2-го типа. Тогда для производства такого количества изделий потребуется затратить
Так как запас сырья данного вида не может превышать 7, то должно выполняться неравенство
Аналогичные рассуждения относительно возможного использования сырья вида B приведут к следующим неравенствам:
При этом так как количество выпускаемой продукции не может быть отрицательной, то
Далее, если будет выпущено х1 единиц продукции 1-го типа, х2 единиц продукции 2-го типа, то прибыль от их реализации составит
Таким образом, приходим к следующей математической задаче: дана система
трёх линейных неравенств с двумя неизвестными хj (j=1..2) и линейная функция относительно этих же переменных
требуется среди всех неотрицательных решений системы неравенств (2) найти такое, при котором функция (3) принимает максимальное значение.
Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.
Так как функция (3) линейная, а система (2) содержит только линейные неравенства, то задача (1)-(3) является задачей линейного программирования.
Заполняем симплекс-таблицу следующим образом:
Если задача на максимизацию, то меняются знаки при целевой функции:
Если задача на минимизацию, то меняются знаки при ограничениях:
В ячейки базисных переменных всегда вписывается единичная матрица. На пересечении строки с коэффициентами целевой функции и столбцов с базисными переменными всегда вписываются нули.
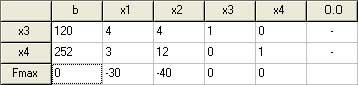
В ходе решения были получена следующая таблица:
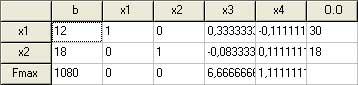
Базисным переменным x1, x2 – присваиваем значения свободных членов. Остальным переменным присваиваем нули.
Значение целевой функции показывается, в левом нижнем углу таблицы.
Таким образом, если предприятие изготовит 12 единиц изделий вида А и 18 единиц изделий В, то оно получит максимальную прибыль, равную: F=30*12 + 40*18 = 1080.
Практическая часть
В соответствии с образцом выполнения работы составить экономико-математическую модель задачи линейного программирования. Затем, используя программу SCalc v1.6, решить задачу линейного программирования в трех режимах. Экспортировать все таблицы, полученные в ходе решения задачи, в Excel.
Сделать экономический анализ оптимального плана.
Результаты оформить в двух файлах следующим образом: первый – экономико-математическая модель задачи линейного программирования – должен быть выполнен в текстовом редакторе WORD, второй файл – решение данной задачи в табличном процессоре EXCEL.
Номер варианта заданий соответствует списочному номеру студента
Источник: studfile.net