В школе на математике мы чаще работаем с цифрами и формулами, чем с чертежами. Пора это исправлять! Чтобы подготовиться к ЕГЭ, нам точно пригодятся графики функции — об этом и поговорим.
24 декабря 2020
· Обновлено 9 декабря 2022
Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnline
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): (-∞; 0) ⋃ (0; +∞).
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
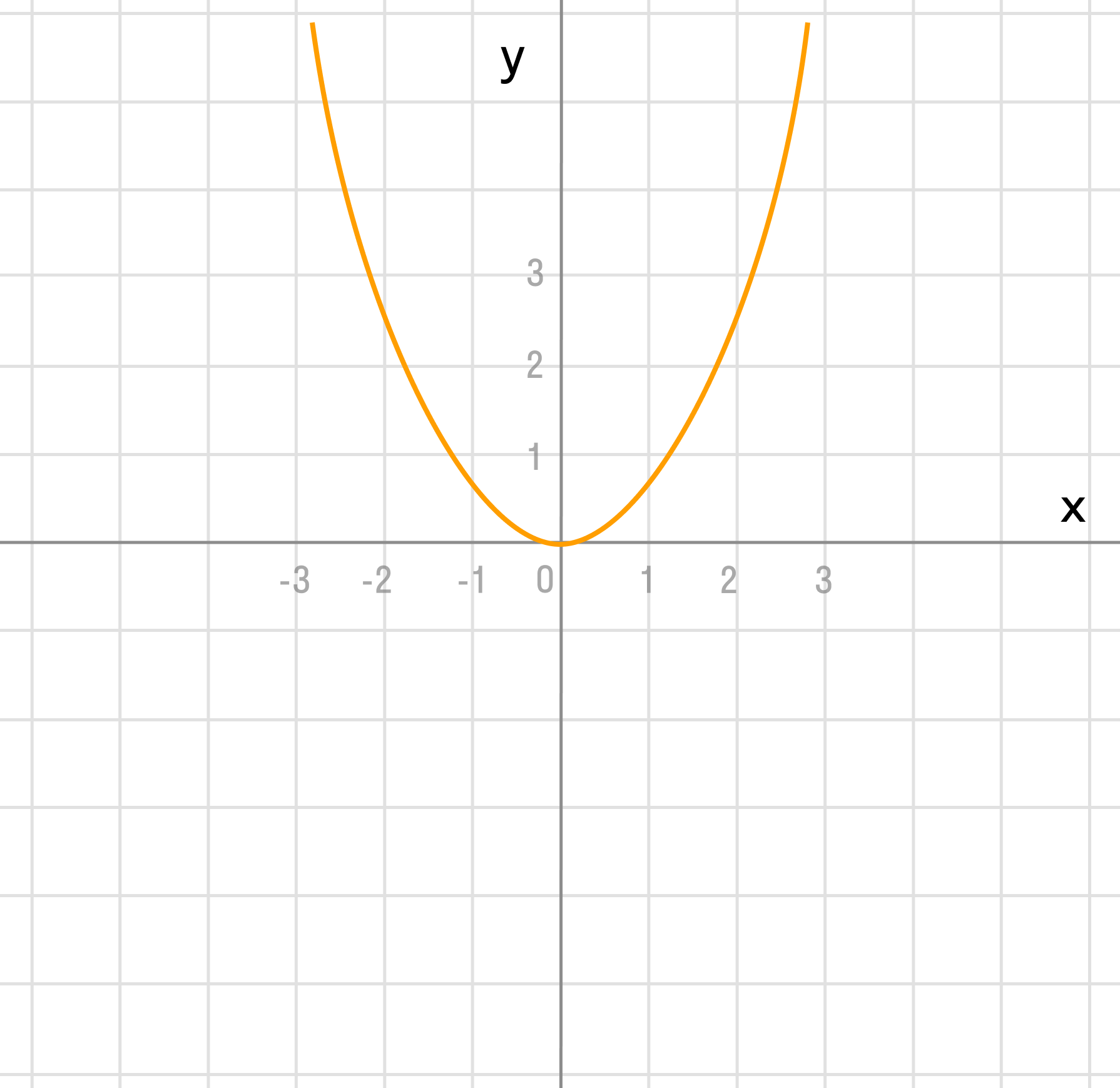
Например, естественная область значений функции y = x 2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Пройти тест!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Создание сложных функций в Microsoft Excel, часть 1
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
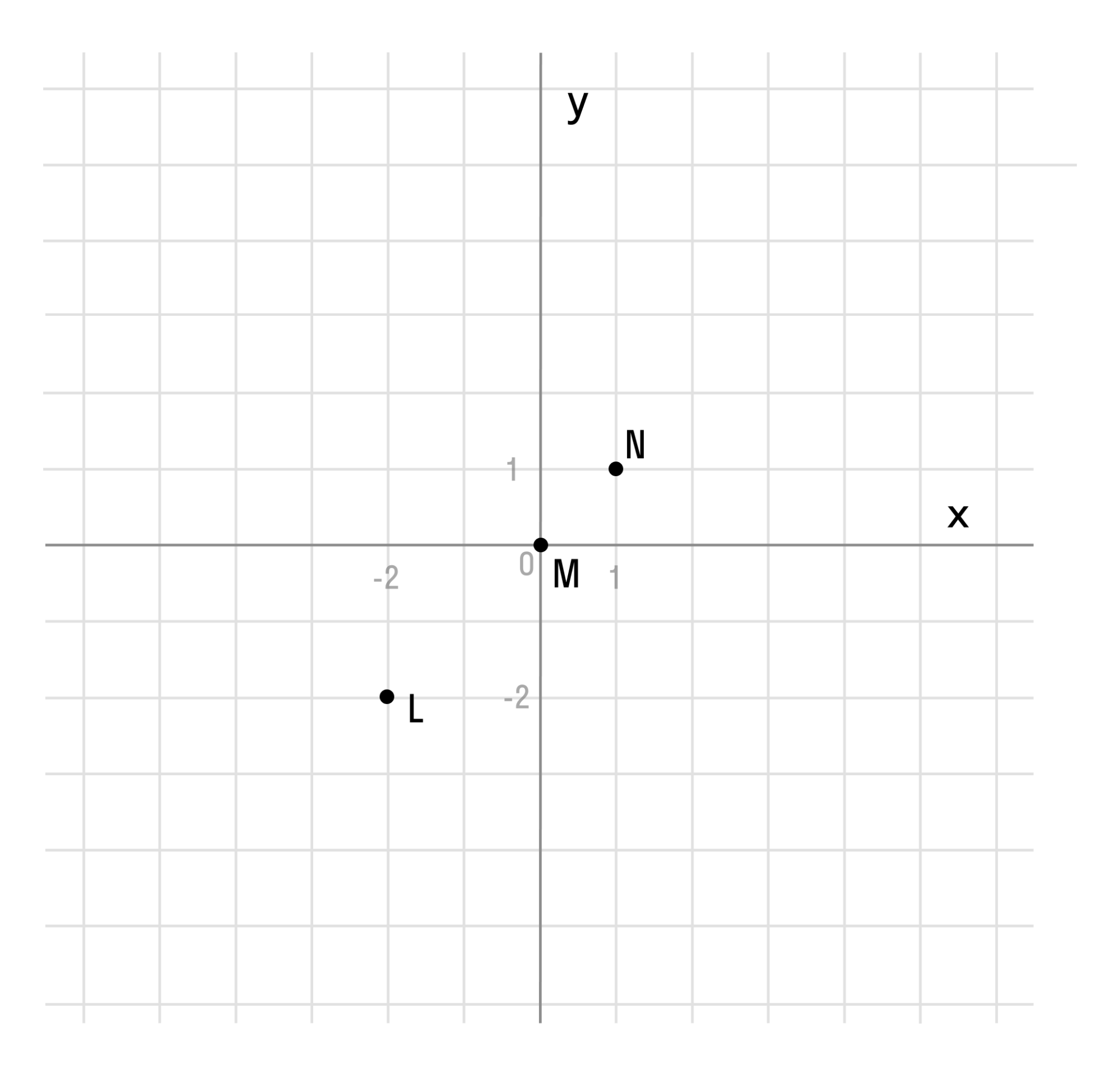
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
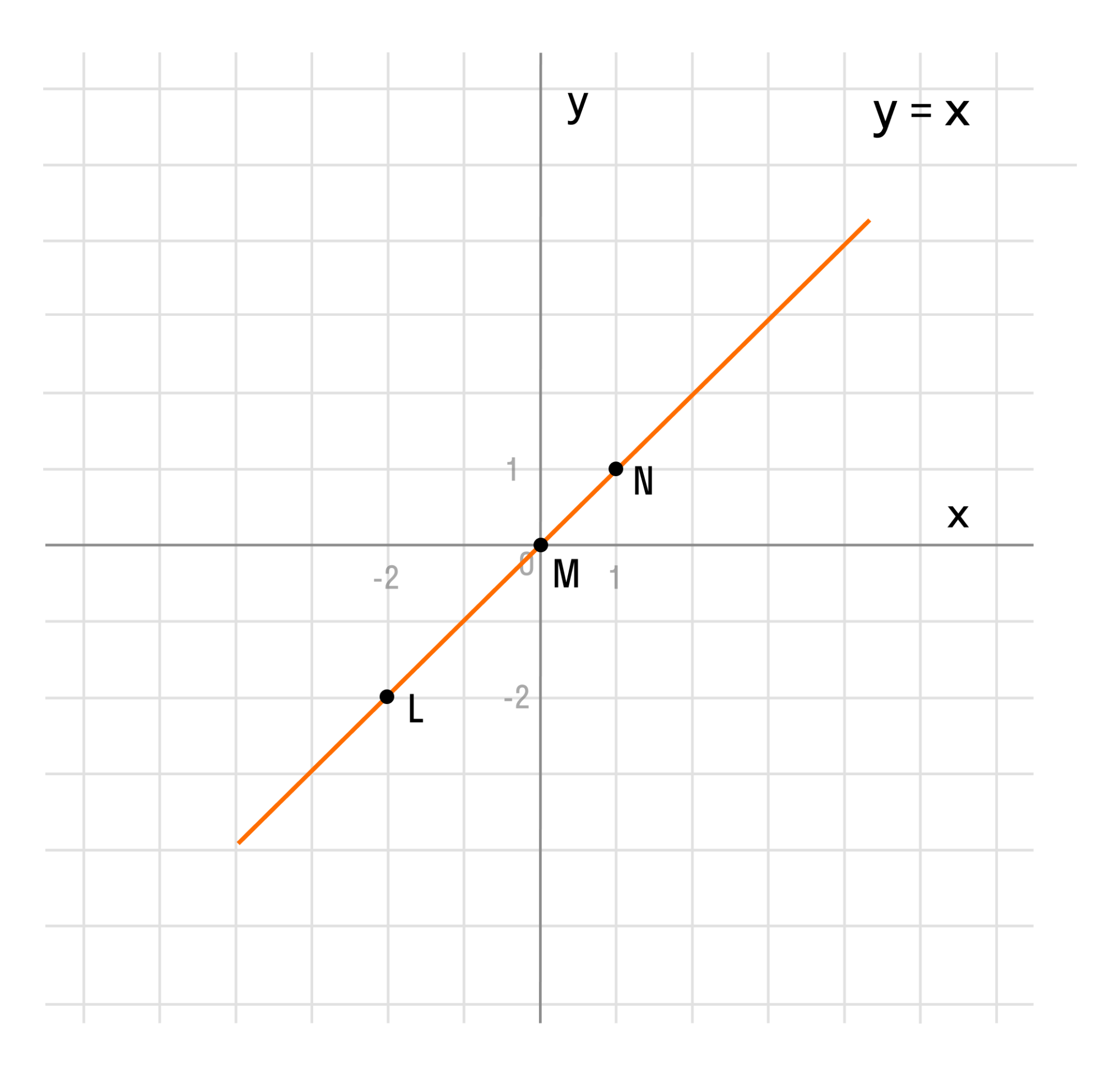
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
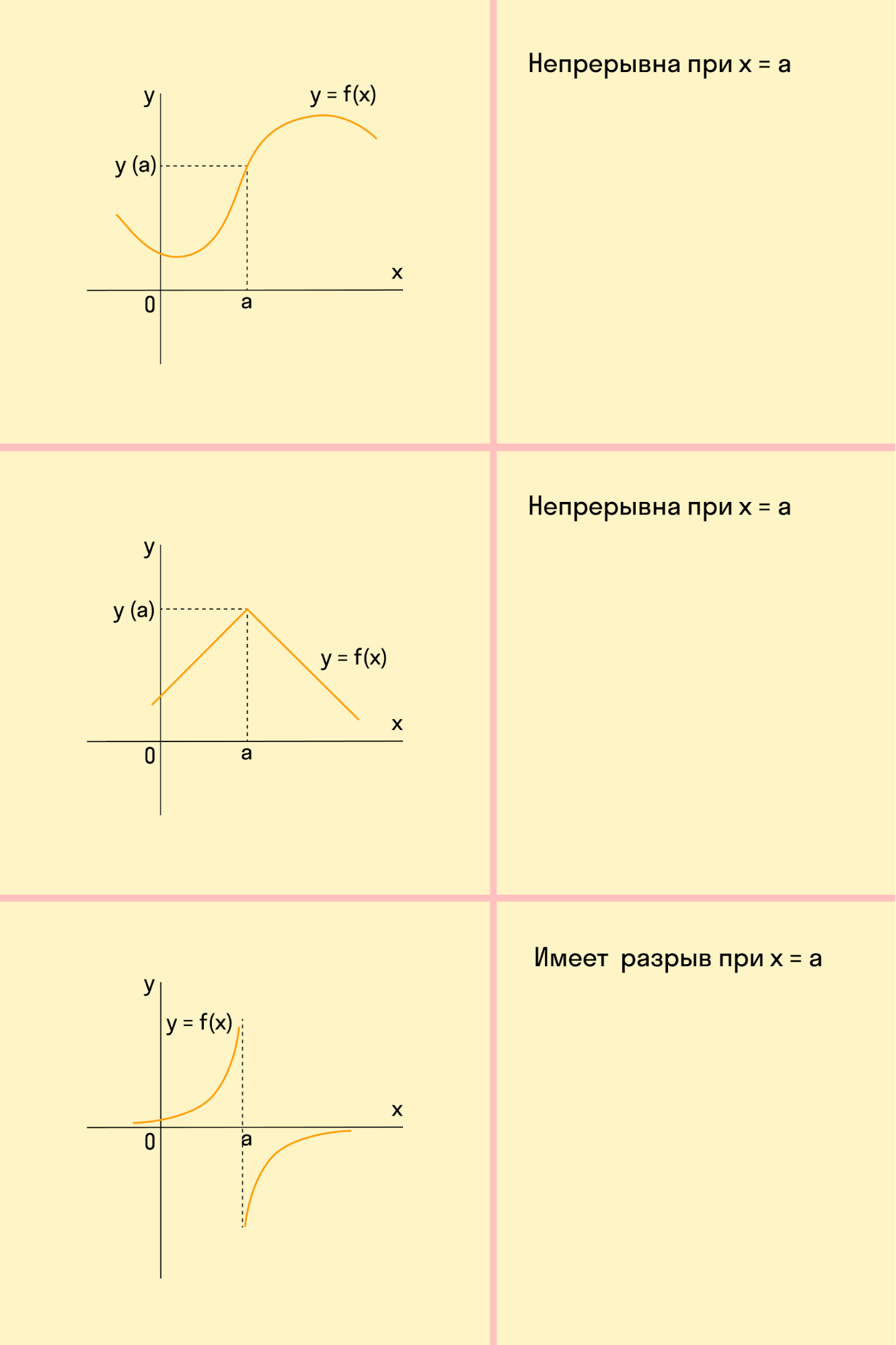
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти точку пересечения с осью OY (если она есть).
- Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
- Промежутки знакопостоянства.
- Асимптоты.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
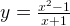
Задача 1. Построим график функции
Упростим формулу функции:
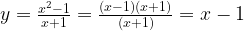
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
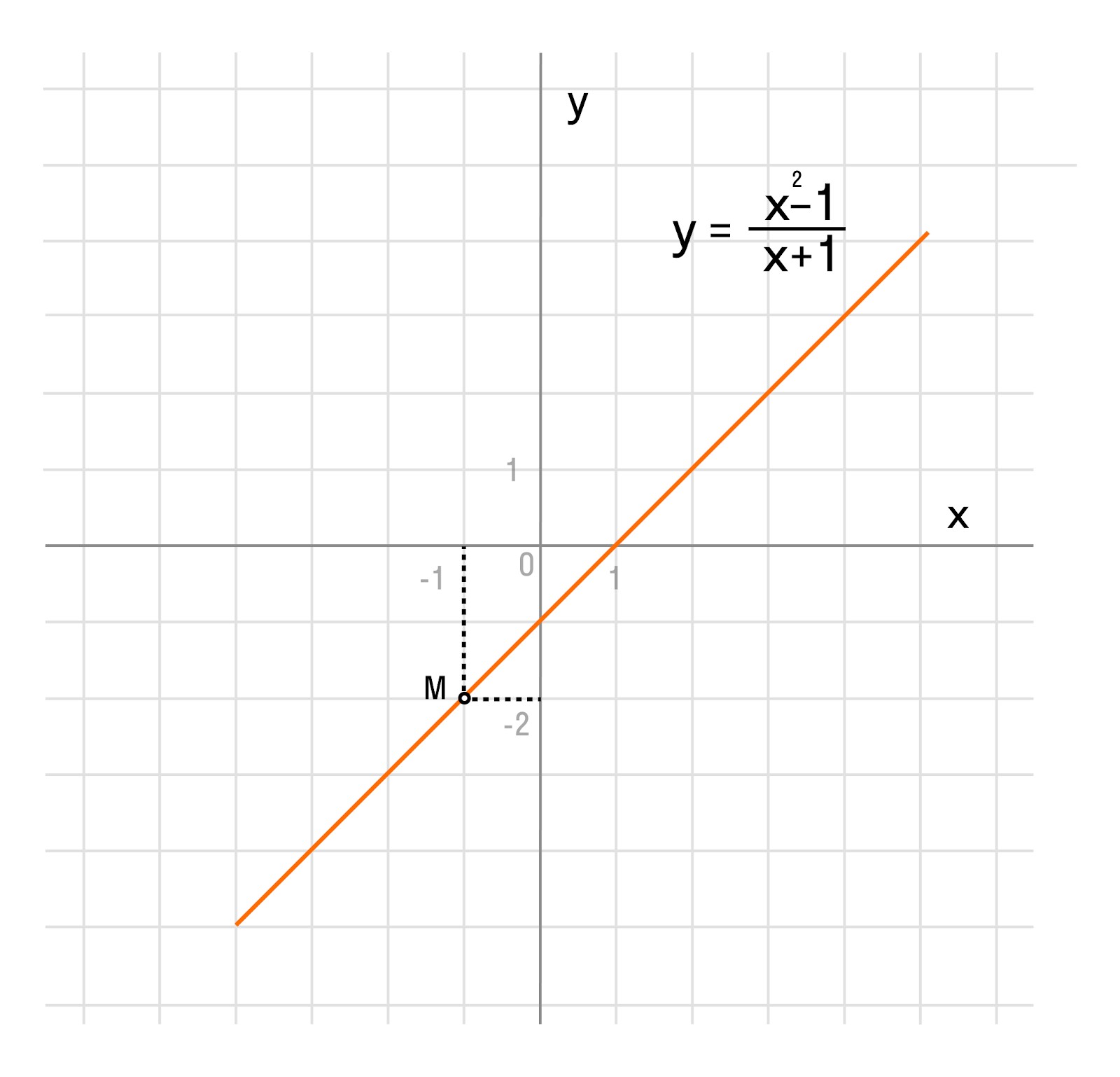
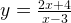
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
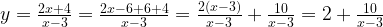
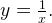
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
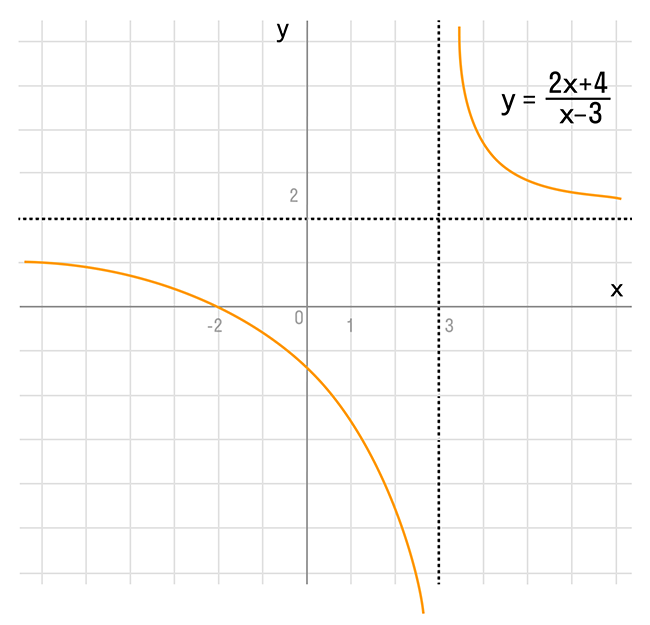
Задача 3. Построить графики функций:
Воспользуемся методом построения линейных функций «по точкам».
| x | y |
| -1 | |
| 1 | 2 |
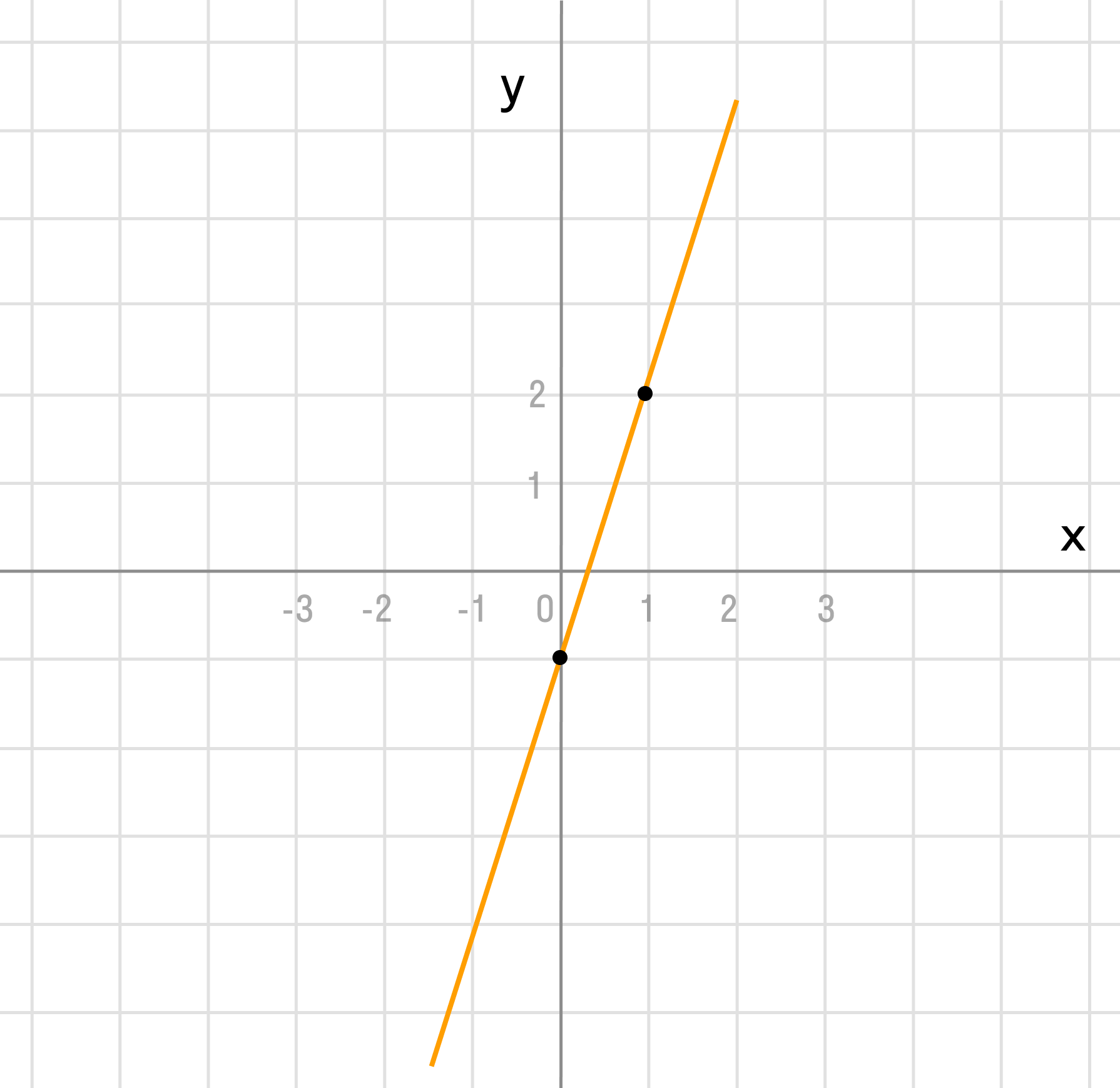
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 2 | |
| 1 | 1 |
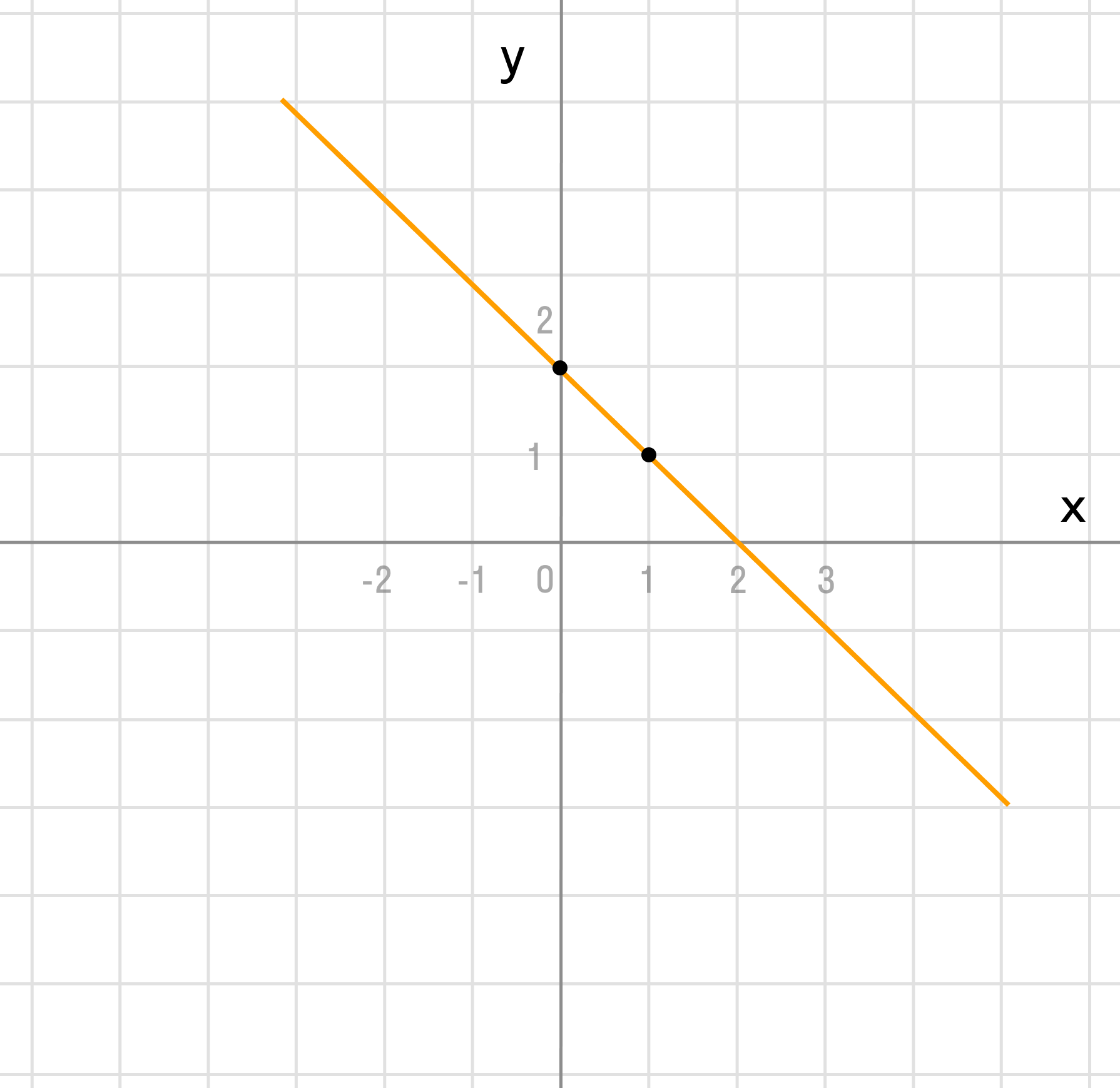
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 2 |
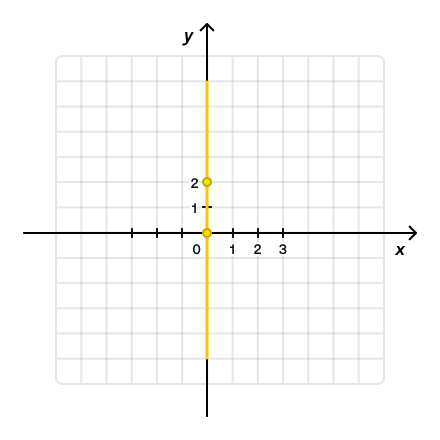
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
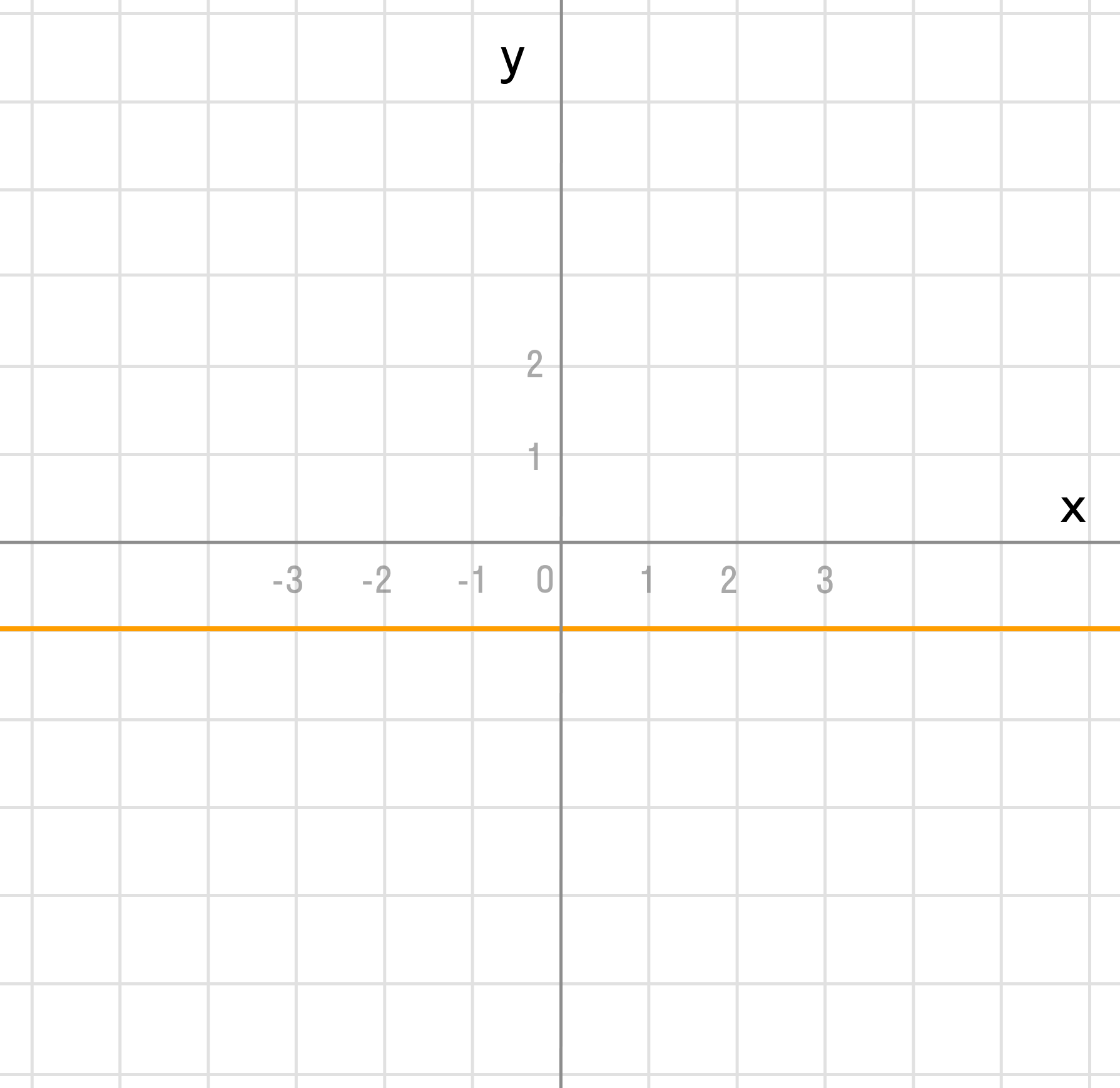
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
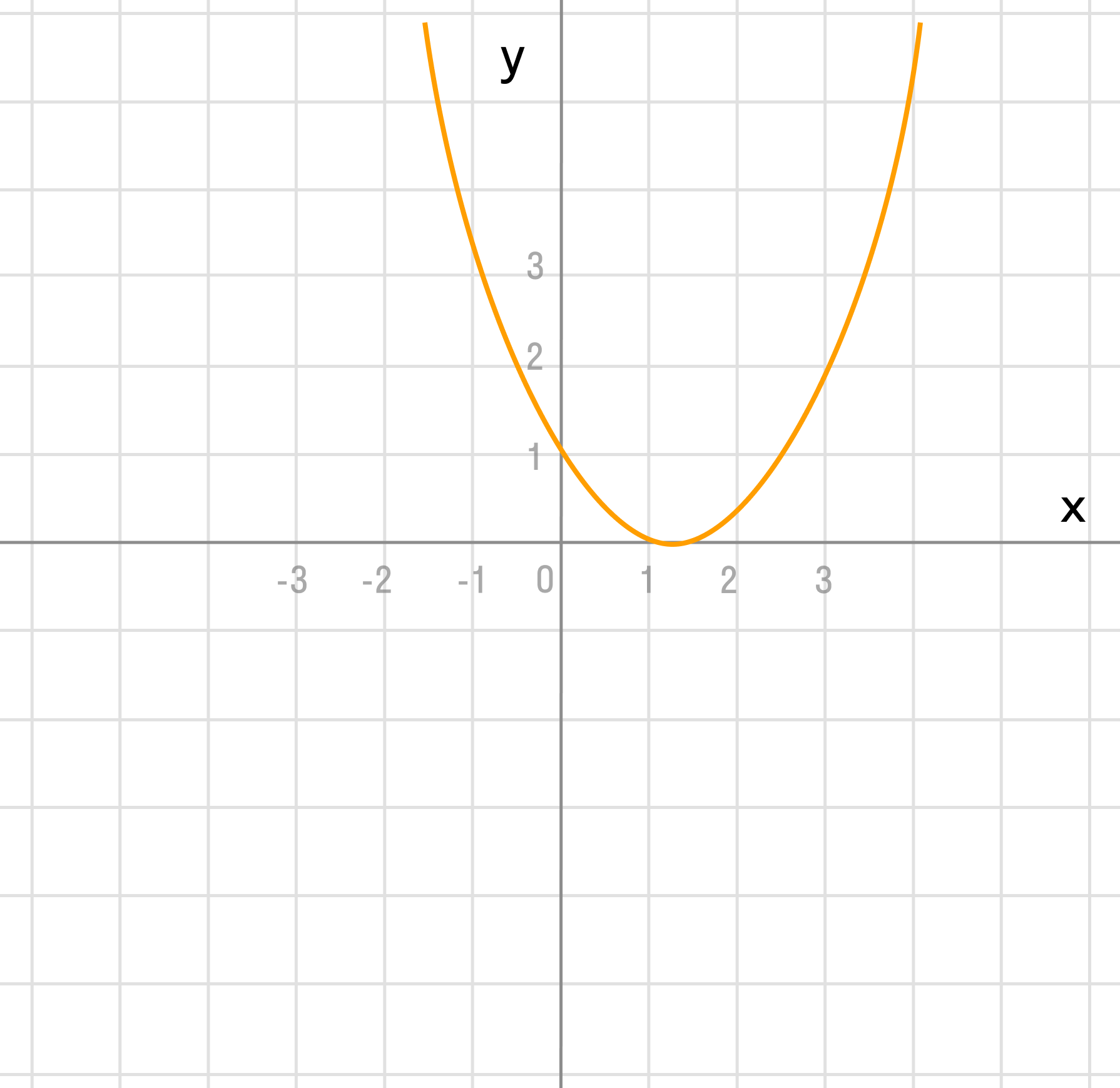
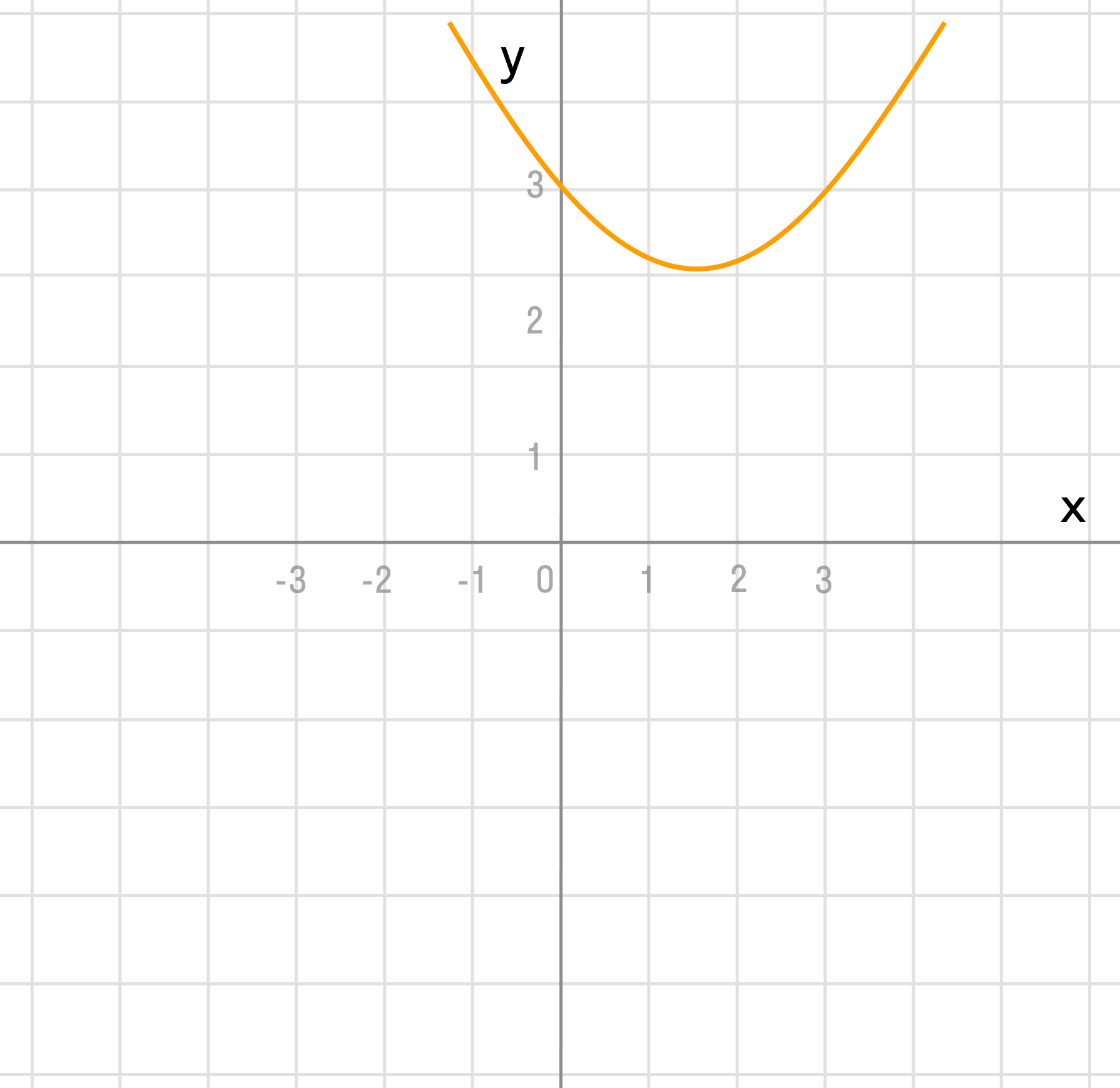
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax 2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
- Ветви вниз, следовательно, a < 0. Точка пересечения с осью Oy — c = 0. Координата вершины
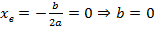
- Ветви вверх, следовательно, a > 0. Точка пересечения с осью Oy — c > 0. Координата вершины
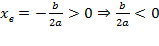, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. - Ветви вниз, следовательно, a < 0. Точка пересечения с осью Oy — c >0. Координата вершины
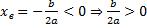, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
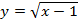
б)
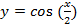
г)
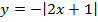
д)
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
- y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
- y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
- y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
- y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
- Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
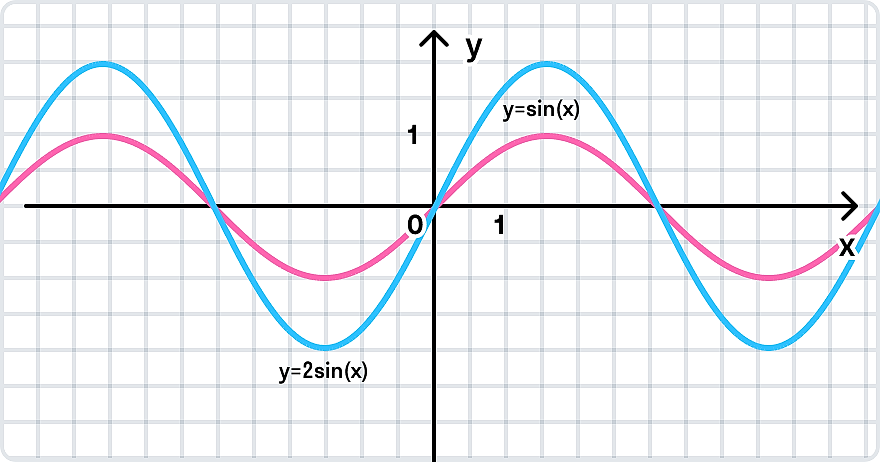
- Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
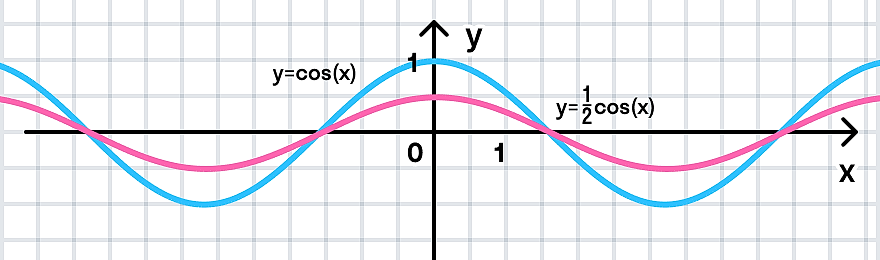
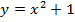
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
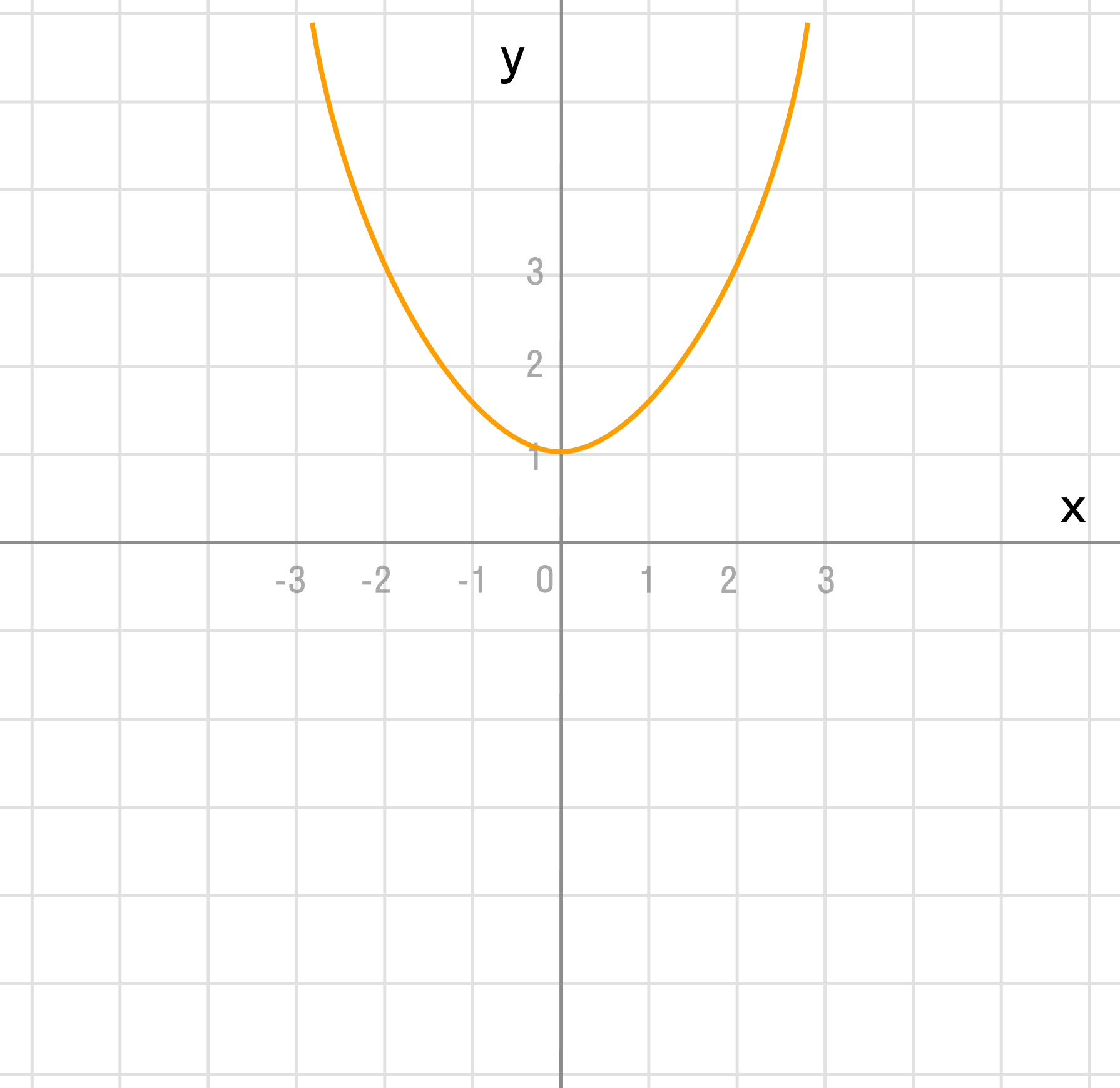
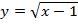
б)
Преобразование в одно действие типа f(x — a).
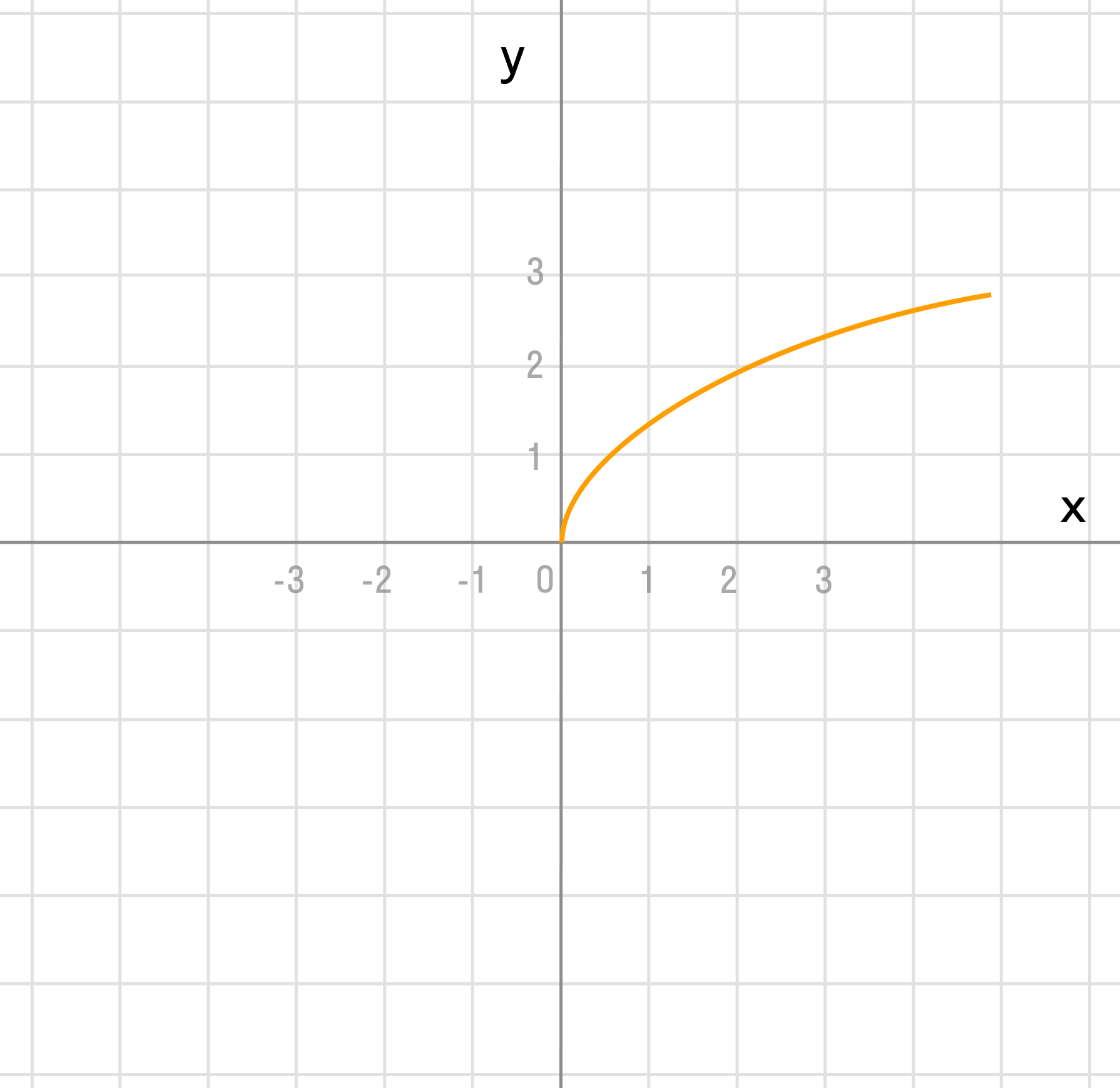
Сдвигаем график вправо на 1:
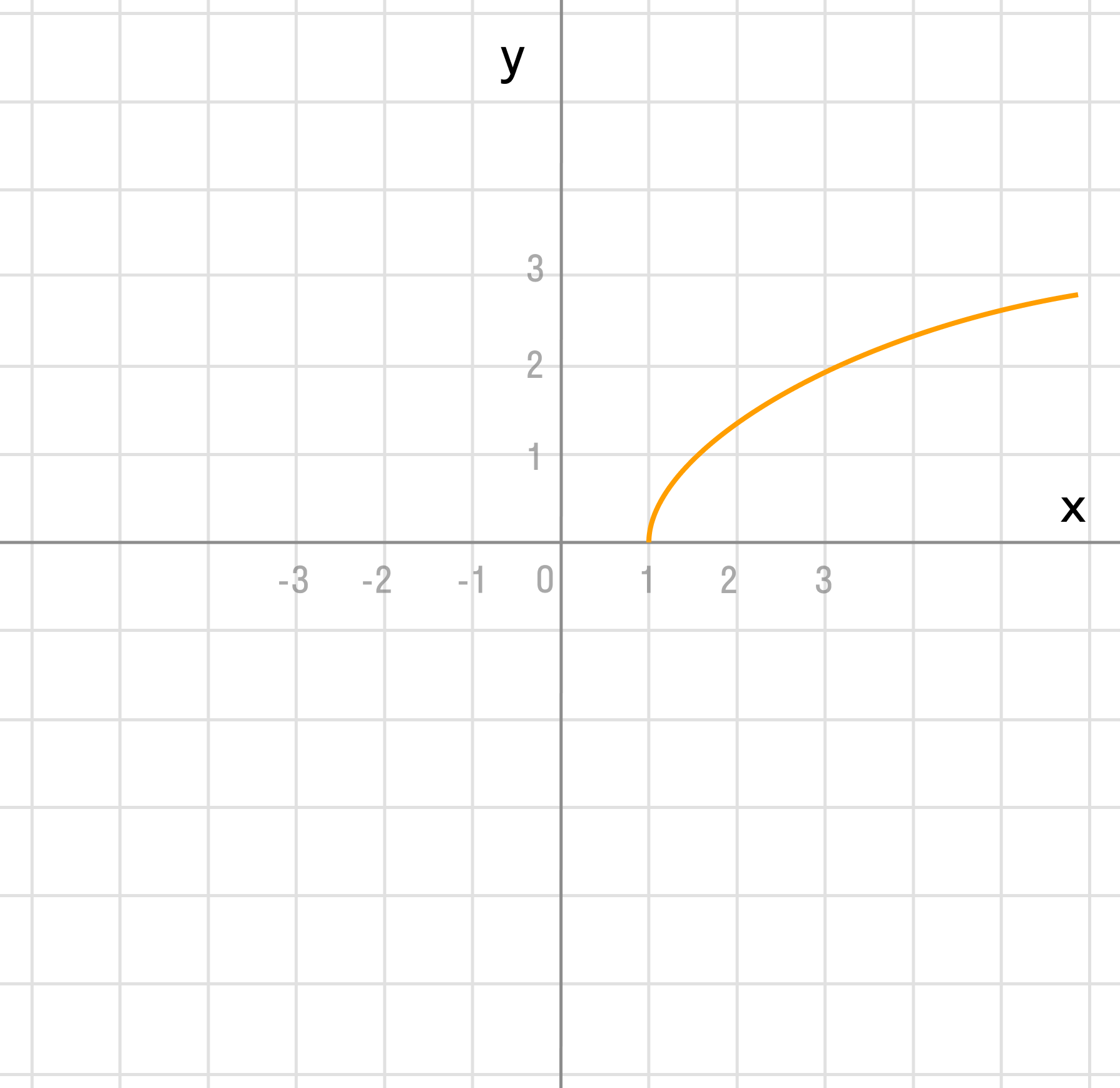
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
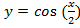
г)
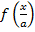
Преобразование в одно действие типа
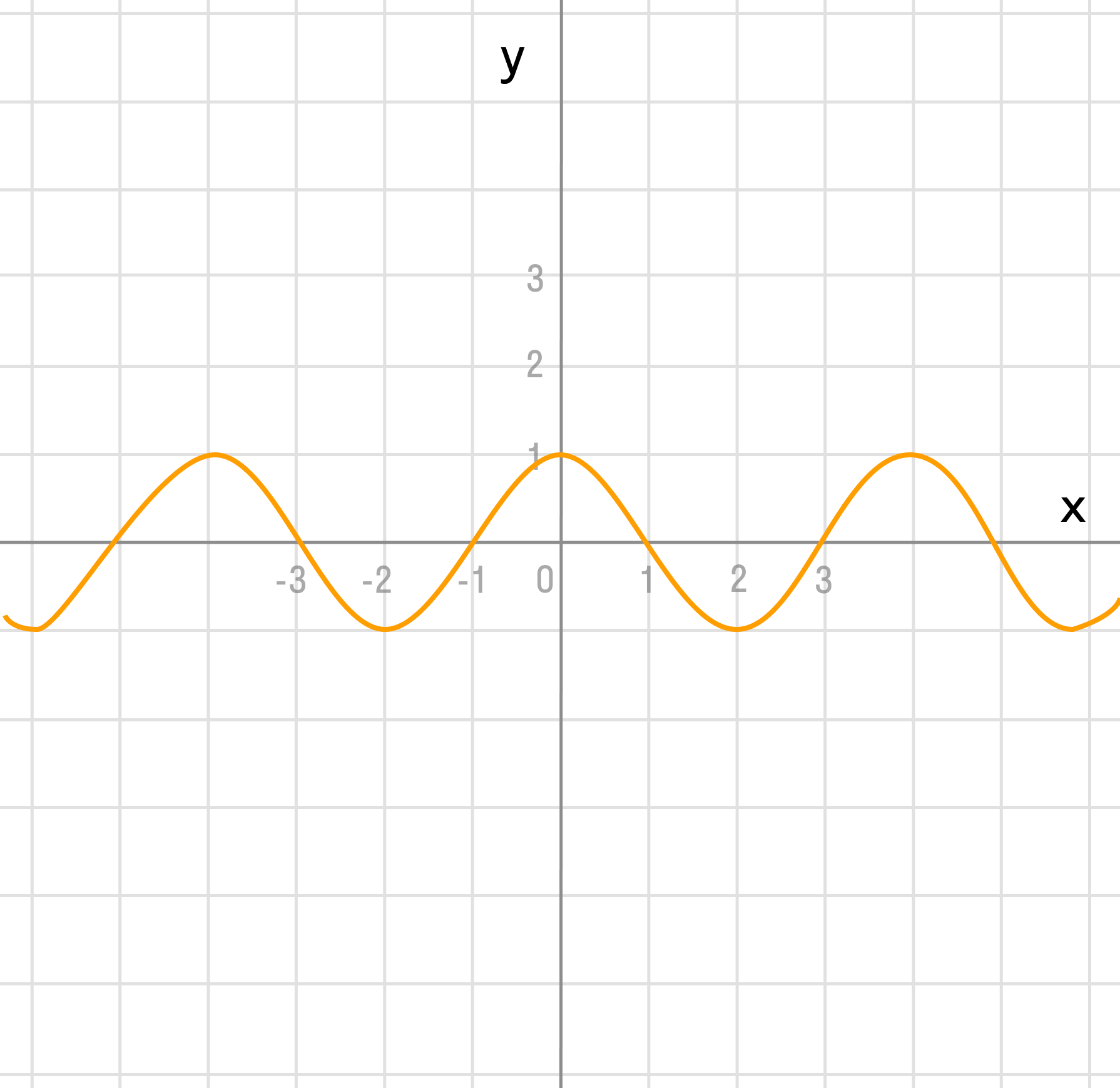
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
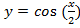
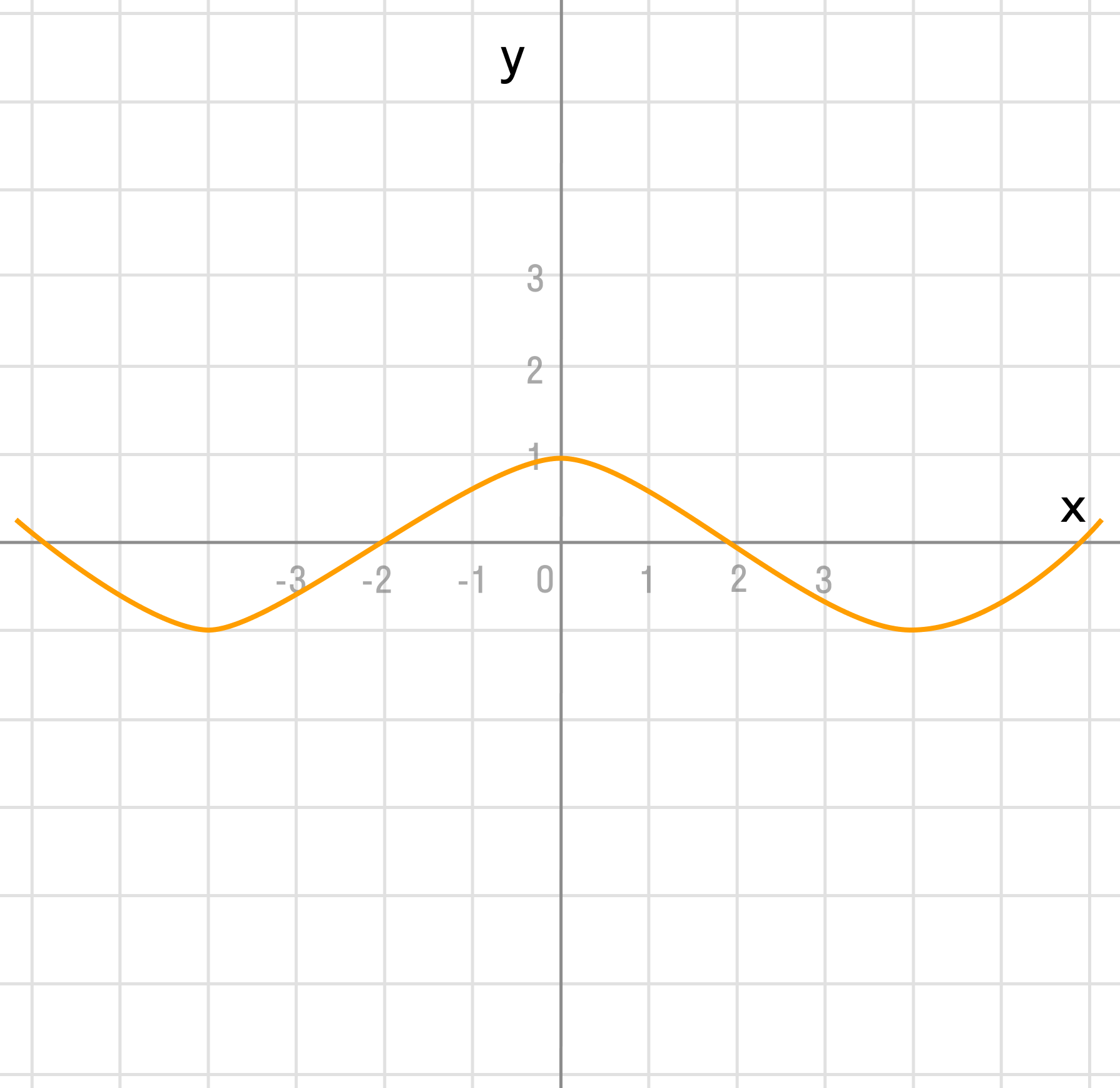
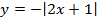
д)
Составить программу для определения значения функции заданной указанным соотношением
Вопрос по информатике:
Рекурсия. ПаскальABC. Составить программу для определения значения функции, заданной указанным соотношением.
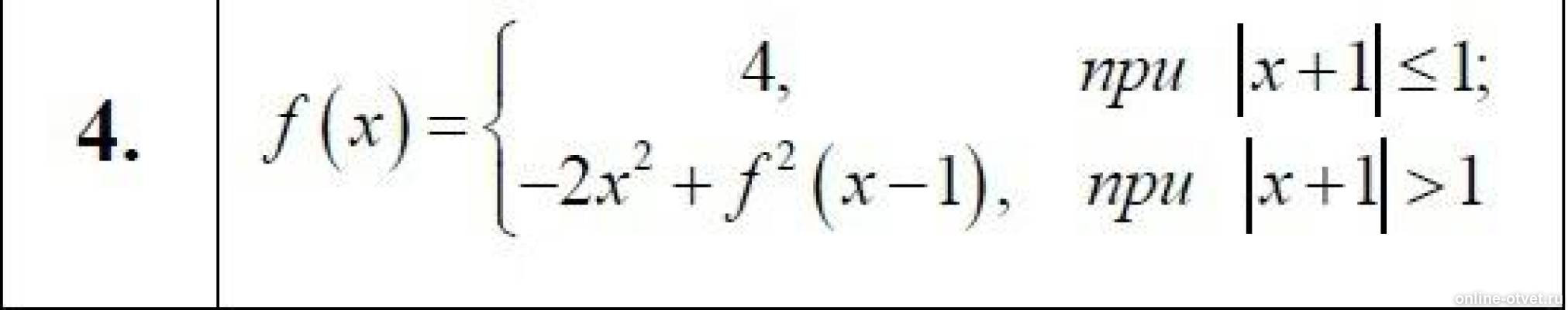
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- bookmark_border
- 05.09.2015 22:19
- Информатика
- remove_red_eye 12990
- thumb_up 42
Ответы и объяснения 2
ghaidedero575
Function F(x : Real) : Real;
Begin
If abs(x+1)>1 then F:=-2*sqr(x)+sqr(f(x-1))
else F:=4;
end;
Var a : Real;
Begin
Readln(a);
Writeln(F(a));
end.
- 07.09.2015 10:10
- thumb_up 31
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.
Источник: online-otvet.ru
Составить программу для определения значения функции заданной указанным соотношением
Написать программу, которая по введенному значению аргумента вычисляет значение функции, заданной в виде графика
Написать программу которая по введенному значению аргумента вычисляет значение функции, заданной в виде графика. Параметр R вводится с клавиатуры.
(Забыл указать в названии, решить задачу надо или на Pascal или c++)
Последний раз редактировалось Grommila.Ice; 27.09.2016 в 02:08 .
Регистрация: 15.02.2010
Сообщений: 15,409
Возьмите листок бумаги и составьте формулу для кусочной функции. Потом в коде через if проверяйте какому куску принадлежит и считайте по нужной формуле.
Участник клуба
Регистрация: 14.05.2016
Сообщений: 1,793
Вот начал делать задание. Уже набрасал шаблон, который нужно чуть-чуть поправить. Нужна твоя помощь.
Я разделил программу на три интервала (с помощью условий «if»:
1-й меньше 0-ля;
2-й от 0-ля до R;
3-й интервал от R и больше).
f_x = 1 + x;
f_x = 2 + x;
f_x = 3 + x;
на то, что тебе нужно для каждого интервала. Например для интервала меньше 0-ля нужна формула прямой, проходящий через две точки (-6;0) и (0;R). Это из алгебры 7 класса. Напиши формулу этой прямой. Для интервалов 2-го и 3-го нужна формула окружности радиуса R (первая с центром в точке (0;0), а вторая с центром точке (R;0),)
Ты понимаешь меня?
Как только изменишь расчет f_x в этих трёх случаях — программа будет решена.
Последний раз редактировалось ura_111; 27.09.2016 в 10:59 .
Источник: www.programmersforum.ru