Составить программу для нахождения расстояния между двумя точками

Пример: есть 2 точки, снятые с помощью GPS-навигатора (или с карты Google), например:

1. 55.755801,37.617887 (знак 0-й километр в Москве)
2. 55.760772,37.60976 (Центральный телеграф, от которого раньше измерялись все расстояния из Москвы)

Какое расстояние между этими точками?

(*в данной задаче кривизной и эллипсоидностью Земли можно пренебречь, и считать радиус Земли — 6400 км или 6360 км — для более точный измерений*).

комментировать
в избранное
4 года назад

Длина окружности меридианов одинакова и равна длине окружности экватора 2*3,14*6360 =39961 км. Если разделить на 360, то получим длину дуги 1 градуса меридиана, 111003 м. Поскольку у нас заданы координаты, то разность широт, умноженная на длину дуги 1 градуса покажет нам расстояние между широтами наших двух точек в метрах: (55,760772-55,755801­ )*111003=551,8 метра.

Поскольку длина окружности каждой широты различная, то нужно вычислить ее для нашей широты, скажем, широты 55,8. Для этого нужно косинус широты умножить на радиус Земли и снова на «двапи»: cos55,8*6360*2*3,14=­ 22461,5 км. Снова делим на 360 градусов и получаем длину дуги 1 градуса широты 55,8 =62393 метра. Определяем расстояние между меридианами наших двух точек: (37.617887-37.60976)­ *62393=507,1 метра.

Расстояние между точками по координатам.

Таким образом, если мы пройдем строго на юг от Центрального Телеграфа 551,8 метра, а потом повернем строго на восток и пройдем еще 507,1 метра, то окажемся у «нулевого километра». Если же по прямой, то нужно знать азимут и длину. Длину определяем по теореме Пифагора как корень из сумы квадратов и получим 749,4 метра. (для тех, кто хочет повторить вычисления, число Пи я здесь брал 3,14, а на калькуляторе нажимал кнопку с символом Пи и будет разный результат.)

система выбрала этот ответ лучшим
в избранное ссылка отблагодарить
lsvnrkywc [0]

Здраствуйте. Я пытаюсь повторить вашу формулу расчёта, но у меня выдаёт 840 метров вместо 749 ваших. Возможно у вас ошибка в расчётах cos55,8*6360*2*3,14?­22461,5 cos55,8*6360*2*pi=29275,32 — 3 месяца назад

lsvnrkywc [0]

сайт отображает не равно как ?-. Всё я нашёл что не так с вашими расчётами у вас написано cos но на практике в формуле стоит cosd сменив косинус я получил близкие к истине 749.65 метров — 3 месяца назад

Источник: www.bolshoyvopros.ru

Составить программу для нахождения расстояния между двумя точками

December 2022 1 80 Report

Напишите программу, которая принимает на вход координаты двух точек и находит расстояние между ними в 3D пространстве.
A (3,6,8); B (2,1,-7), -> 15.84
A (7,-5, 0); B (1,-1,9) -> 11.53

Answers y₁; z₁) и A₂(x₂; y₂; z₂) можно вычислить по формуле:

Расстояние между точками

В итоге получаем код, в котором сначала запрашиваются координаты первый точки, после — второй. Высчитывается расстояние между этими точками с точностью до сотых и выводится результат.

Источник: scholar.tips

Расстояние между двумя точками онлайн

С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.

Предупреждение

Очистить все ячейки?
Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Расстояние между двумя точками на прямой

Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.

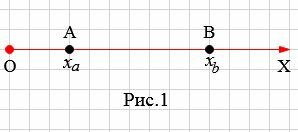Расстояние между точками A и В равно:

( small AB=OB-OA. )

(1)

Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:

( small AB=x_b-x_a . )

(2)

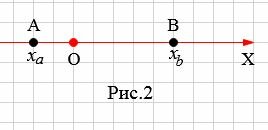На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:

( small AB=OB+OA. )

(3)

Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:

( small AB=x_b+|x_a|=x_b-x_a . )

(4)

На рисунке 3 точки A и В находятся c левой стороны начала координат O.

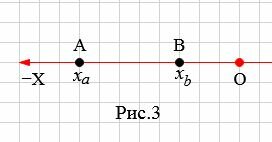B этом случае рассояние между точками A и B равно:

( small AB=OA-OB. )

(5)

Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:

( small AB=|x_a|-|x_b|=x_b-x_a . )

(6)

Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).

Формулы (2),(4),(6) можно записать и так:

( small AB=|x_b-x_a|= |x_a-x_b| . )

(7)

Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):

( small AB=|x_b-x_a|= |7-(-4)|=11 . )

(7)

Расстояние между двумя точками на плоскости

Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).

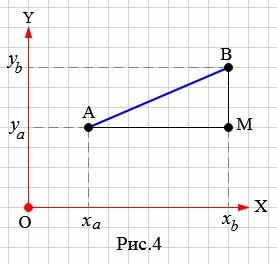Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:

( small AM=x_b-x_a,;; BM=y_b-y_a. )

(8)

ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:

( small AB^2=AM^2+BM^2. )

Тогда, учитывая (8), получим:

( small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. )

( small AB=sqrt . )

(9)

Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:

,

.

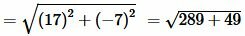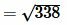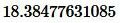
Ответ: .

Расстояние между двумя точками в пространстве

Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).

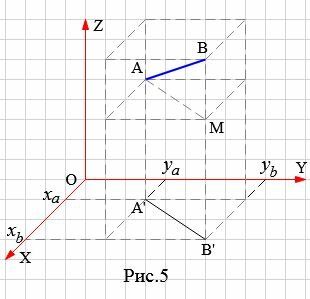AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:

( small AB^2=AM^2+BM^2. )

(10)

Учитывая, что BM равно разности третьих координат точек B и A, получим:

( small BM=z_b-z_a. )

Из предыдующего параграфа следует, что:

( small A’B’^2=(x_b-x_a)^2+(y_b-y_a)^2. )

(11)

Но AM=A’B’. Тогда из (10) и (11) следует:

( small AB^2=AM^2+BM^2=A’B’^2+BM^2 ) ( small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. )

( small AB= sqrt. )

(12)

Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:

,

.

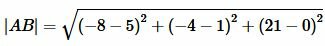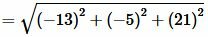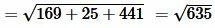Ответ: .

• Расстояние между двумя точками онлайн
• Общее уравнение прямой на плоскости
• Каноническое уравнение прямой на плоскости
• Параметрическое уравнение прямой на плоскости
• Уравнение прямой в отрезках
• Нормальное уравнение прямой
• Отклонение точки от прямой
• Пучок прямых. Уравнение пучка прямых
• Общее уравнение плоскости
• Уравнение плоскости в отрезках
• Нормальное уравнение плоскости
• Уравнение прямой, проходящей через две точки онлайн
• Проекция точки на прямую онлайн
• Расстояние от точки до прямой онлайн
• Расстояние между прямыми на плоскости онлайн
• Расстояние между прямыми в пространстве онлайн
• Точка пересечения прямых на плоскости онлайн
• Точка пересечения прямых в пространстве онлайн
• Точка пересечения прямой и плоскости онлайн
• Линия пересечения плоскостей онлайн
• Угол между прямыми онлайн
• Угол между прямой и плоскостью онлайн
• Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн
• Уравнение плоскости онлайн
• Проекция точки на плоскость онлайн
• Расстояние от точки до плоскости онлайн
• Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
• Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
• Уравнение плоскости, проходящей через точку и прямую онлайн
• Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
• Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн
• Расстояние между плоскостями. Онлайн калькулятор
• Угол между плоскостями. Онлайн калькулятор

• Новые калькуляторы
• Инженерный калькулятор онлайн
• Решение треугольников онлайн
• Радиус описанной окружности около треугольника онлайн

Источник: matworld.ru