Составить программу для машины тьюринга

Машина Тьюринга — абстрактная вычислительная машина, предложенная Аланом Тьюрингом для формализации понятия алгоритма. Устройство МТ состоит из следующий частей:

• бесконечная лента, состоящая из ячеек
• головка для считывания/записи символов на ленте
• устройство управления

Бесконечная лента

Лента в машине Тьюринга состоит из ячеек, в которые можно записывать символы из заданного алфавита, а также считывать их. Если на ленте ничего не записано, то считается, что там записан специальный символ λ . Данный символ дополняет алфавит, но не входит в него явным образом.

Обычно на ленту в начале работы помещают входное слово. В процессе работы машины Тьюринга содержимое ленты модифицируется устройством управления и в результате на ленте остаётся выходное слово.

Считывающая/записывающая головка

В каждой машине Тьюринга есть специальная головка, указывающая на одну определённую ячейку на ленте. Данное устройство позволяет считывать символ с ячейки, над которой находится, или записывать символ в эту ячейку. Также головка может перемещаться влево и вправо на одну ячейку, или оставаться на месте.

Как запрограммировать на машине Тьюринга сложение? Душкин объяснит

Устройство управления

Под устройством управления понимается таблица состояний и правил перехода для машины Тьюринга. Состоянием называется строка таблицы, в которой в данный момент находится машина. Состояние, в котором находится машина перед запуском называется начальным, обычно обозначается именем q0 . Для завершения работы МТ используется специальное терминальное состояние, которое обозначается как ! .

Таблица имеет размер |Q|x|A| , где |Q| — количество состояний, а |A| — размерность алфавита (включая символ λ ). В первой (заголовочной) строке написаны символы алфавита. В каждой из ячеек таблицы, относящихся к строкам с состояниями, располагаются тройки , определяющие действие машины, которое она должна сделать, если находится в данном состоянии и на ленте записан символ из заголовочной ячейки данного столбца:

• char — символ, который нужно записать на ленту
• action — действие, которое нужно совершить после записи (одно из трёх действий: L — сдвиг влево, N — остаться на месте, R — сдвиг вправо)
• state — состояние, в которое необходимо перейти

Допускаются краткие записи для правил:

• Если необходимо выполнить только сдвиг, оставшись в том же состоянии, то достаточно записать только символ перемещения: L , N или R
• Если нужно выполнить останов, то достаточно записать !
• Если нужно записать пустой символ ( λ ), то можно поставить пробел или запятую перед символом сдвига: ,R,q0

Примеры машин Тьюринга

Пример 1 (загрузить в эмулятор). К двоичному числу прибавить 1. В начальный и конечный момент головка должна находиться на самом старшем бите слова (слева).

Q A01λ

q0	R	R	λ L q1
q1	1 N q2	0 L q1	1 N !
q2	L	L	λ R !

Конструирование машины Тьюринга

Так как изначально по условию головка МТ находится на самом старшем бите, а увеличивать надо младший, необходимо сначала переместить головку на младший бит, что выполняется в состоянии q0: как только лента увидит символ λ, она сдвинется влево (на младший бит) и перейдёт в состояние икремента (q1).

В состоянии q1 возможны следующие ситуации:

• младший бит равен 0, его нужно заменить на 1 и переместить головку на старший бит (через состояние q2)
• младший бит равен 1, его нужно заменить на 0, сдвинуться левее и остаться в этом же состоянии
• в процессе замены 1 на 0 достигнут пустой символ (было записано число из одних единиц), вместо него надо записать 1 и остановить МТ

Состояние q2 нужно лишь для выполнения условия остановки головки на старшем бите. Оно полностью аналогично начальному состоянию, только движение происходит в левюу сторону и при достижении пустого символа головка сдвигается вправо и выполняется останов.

Пример 2 (загрузить в эмулятор). В слове из алфавита инвертировать символы. В начальный момент головка находится в начале слова.

Q Aabλ

q0	b R q0	a R q0	!

До тех пор, пока под головкой не окажется пустой символ, вместо символа a записывается символ b , а вместо b записывается a и выполняется сдвиг головки вправо на очередной символ.

Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.

Источник: programforyou.ru

Машина Тьюринга онлайн — Python

Клас­си­ка — сту­ден­там пред­ла­га­ют за­да­чи с ма­ши­ной Тью­рин­га. Ча­сто тре­бу­ет­ся со­ста­вить про­грам­му для ма­ши­ны Тью­рин­га в ви­де таб­ли­цы по­сле­до­ва­тель­ных опе­ра­ций. Тео­рии про ма­ши­ну мно­го в ин­тер­не­те. Но все­гда воз­ни­ка­ет во­прос: за­чем сту­ден­ту про­грам­ми­сту на­до по­ни­мать как ра­бо­та­ет эта из­вест­ная ма­ши­на?

От­вет бу­дет та­ким: в ма­шине ре­а­ли­зо­ван ал­го­ритм, поз­во­ля­ю­щий чи­тать и вы­пол­нять некую про­стую про­грам­му на аб­стракт­ном язы­ке. По су­ти: ма­ши­на Тью­рин­га некий про­об­раз мно­гих ал­го­рит­мов и да­же прин­ци­пов ра­бо­ты ком­пью­те­ра. Не по­нят­но? Боль­ше про Тью­рин­га чи­тай­те здесь.

Ре­а­ли­стич­ный при­мер за­дач

За­да­ча 1. В ауди­то­рии си­дят сту­ден­ты по спис­ку. За­хо­дит но­вый сту­дент с фа­ми­ли­ей на бук­ву «К» и ему на­до сесть за по­след­ним сту­ден­том, у ко­то­ро­го то­же фа­ми­лия на бук­ву «К». Все сту­ден­ты на бук­ву «К» си­дят один за дру­гим по­сле­до­ва­тель­но.

За­да­ча 2. Вы по­сла­ли в сто­ло­вую на пе­ре­ры­ве гон­ца из ва­шей груп­пы, чтобы за­нять оче­редь. Так сде­ла­ли все груп­пы. Те­перь, ко­гда в сто­ло­вую на пе­ре­ры­ве при­хо­дят сту­ден­ты из раз­ных групп, им на­до вы­стро­ить­ся в оче­редь в со­от­вет­ствии с гло­баль­ной оче­ре­дью групп, но стать в пре­де­лах сво­ей груп­пы в ко­нец оче­ре­ди в груп­пе.

За­да­ча 3. Тек­сто­вый файл со­зда­ет­ся в ви­де строк. Но­вые за­пи­си до­бав­ля­ют­ся в то ме­сто фай­ла, где за­пи­са­ны стро­ки той же дли­ны, что и но­вая до­бав­ля­е­мая стро­ка. Но­вая стро­ка до­бав­ля­ет­ся в ко­нец спис­ка оди­на­ко­вых с ней строк по длине.

По­про­буй­те за­пи­сать ал­го­ритм ре­ше­ния пе­ре­чис­лен­ных за­дач, при­ду­мав некий свой на­бор ко­манд, ко­то­рые на­до вы­пол­нить ко­му-то. На­при­мер, вхо­дя­щий сту­дент дол­жен дей­ство­вать по ва­ше­му ал­го­рит­му, пы­та­ясь сесть в пра­виль­ное ме­сто. Воз­мож­но для каж­дой из за­дач у вас бу­дет свой на­бор ко­манд и свой ал­го­ритм. Так вот, ва­ша ма­ши­на Тью­рин­га долж­на по­ни­мать но­вый на­бор ко­манд и ал­го­ритм, за­пи­сан­ный с по­мо­щью это­го на­бо­ра ко­манд. Ну вот та­кое по­лу­чи­лось по­яс­не­ние тем, кто ищет в ин­тер­не­те — «ма­ши­на тью­рин­га про­сты­ми сло­ва­ми» или «ма­ши­на тью­рин­га для чай­ни­ка».

Ими­та­ция ма­ши­ны Тью­рин­га. Язык Python

В при­ве­ден­ных при­ме­рах есть по­греш­ность — лен­та ма­ши­ны Тью­рин­га тут не бес­ко­неч­ная. Хо­тя ес­ли счи­тать что сту­ден­ты мо­гут хо­дить в сто­ло­вую бес­ко­неч­но, то то­гда все на сво­их ме­стах. Но мы бу­дем ими­ти­ро­вать ма­ши­ну Тью­рин­га для слу­чая ко­неч­ной лен­ты.

R=+1 L=-1 S=0 per=0 move=1 step=2 spisok=list(‘0001111000’) def TM(code, lenta, start, cell): state = start while (True): rows = code[state] row = rows[int(lenta[cell])] lenta[cell] = row[per] if not row[move]: break cell += row[move] state = row[step] return lenta rez = TM({ ‘A’ : ((0, R, ‘A’), (1, R, ‘B’)), ‘B’ : ((1, S, ‘C’), (1, R, ‘B’)), ‘C’ : ((0, S, ‘C’), (1, S, ‘C’))}, spisok,»A»,0) print(rez)

Just press ‘Run’.

В ре­зуль­та­те ра­бо­ты ма­ши­ны Тью­рин­га, из­на­чаль­ный спи­сок:

0001111000

бу­дет до­пол­нен еди­ни­цей и по­лу­чит та­кой вид:

00011111000

При­ве­дем даль­ше неко­то­рые по­яс­не­ния к ко­ду. Итак, у нас име­ет­ся на­бор ко­манд неко­то­ро­го язы­ка.

R = +1 # впра­во на еди­ни­цу L = -1 # вле­во на еди­ни­цу S = 0 # — стоп

Даль­ше обо­зна­че­ния для по­зи­ции эле­мен­та (ин­дек­са) в лен­те (lenta) для те­ку­ще­го ря­да таб­ли­цы.

per=0 move=1 step=2

Даль­ше у нас спи­сок, ко­то­рый со­от­вет­ству­ет стар­то­во­му со­сто­я­нию (вход) лен­ты ма­ши­ны Тью­рин­га. Вы мо­же­те его ме­нять в на­шем ко­де и сра­зу смот­реть на ре­зуль­тат по­сле вы­пол­не­ния про­грам­мы.

spisok=list(«0001111000»)

Даль­ше — са­ма функ­ция или ма­ши­на Тью­рин­га с та­ки­ми па­ра­мет­ра­ми: code — про­грам­ма: lenta — лен­та ма­ши­ны Тью­рин­га, start — на­чаль­ное со­сто­я­ние; cell — на­чаль­ная по­зи­ция на лен­те.

def TM(code, lenta, start, cell):

Даль­ше идет за­пуск ма­ши­ны с на­чаль­ны­ми дан­ны­ми.

rez = TM({ ‘A’ : ((0, R, ‘A’), (1, R, ‘B’)), ‘B’ : ((1, S, ‘C’), (1, R, ‘B’)), ‘C’ : ((0, S, ‘C’), (1, S, ‘C’))}, spisok,»A»,0)

Вы мо­же­те ме­нять: spisok, на­чаль­ное со­сто­я­ние — «A», на­чаль­ную клет­ку лен­ты — «0». Но и ко­ман­ды и про­грам­му то­же мож­но про­бо­вать ме­нять.

P.S. Код ма­ши­ны из ин­тер­не­та, пер­во­ис­точ­ник най­ти не уда­лось.

Источник: qaweb.dev

§1. История создания машины Тьюринга

Алан Мэтисон Тьюринг ˗ английский математик, криптограф, логик, оказавший огромное влияние на развитие информатики. Данный ученый родился в 1912 году недалеко от Лондона и прожил достаточно короткую, внешне не очень яркую, но чрезвычайно насыщенную практическими и интеллектуальными достижениями жизнь.

Заслуги Алана Тьюринга по расшифровке немецких военных кодов, которые спасли жизни сотен тысяч людей, во время Второй мировой войны были проигнорированы. Однако официальные публичные извинения были принесены только спустя 55 лет после его смерти. Математика с его смертью лишилась одного из самых ярких и оригинальных мыслителей. Алан М. Тьюринг не только решил одну из труднейших математических проблем, а фактически он предложил намного большее – новый метод решения математических задач (машину Тьюринга), который в конечном счете привел к возникновению computer science и современных компьютеров.

Алан Тьюринг стоял у самых истоков искусственного интеллекта и программирования. У данного ученого него не было учеников в общепринятом смысле, но определенно можно утверждать, что любой программист или же человек, непосредственно связанный с информатикой, даже не осознавая того, является если и не учеником, но уж точно его последователем. Именем Алана Тьюринга названа своего рода Нобелевская премия в области computer science , которая называется премией Тьюринга. Данной награды удостаиваются те, кто внес выдающийся вклад в эту область исследований.

Для решения любой проблемы не надо думать, и уж тем более ˗ угадывать, именно к этому сводятся большинство исследований этого ученого, а достаточно разработать определенный метод. Правильное решение можно будет получить гораздо быстрее, если механически следовать этому порядку действий. Алан Тьюринг ввел понятие «определительного метода», который позже получил название «алгоритм», а так же разработал свои собственные логические ходы.

В 1936 году этим ученым была построена логическая модель знаменитой машины, которая и называется машиной Тьюринга. Необходимо заметить и то, что в те годы под словом «Computer» подразумевался человек, проводящий однообразные вычисления по определенным инструкциям. Например, так называли бухгалтеров, счетоводов. Идея Алана Мэтисона Тьюринга состояла в том, что для проведения данных действий присутствие человека не требуется.

Предыстория создания этой работы связана с формулировкой Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900 году неразрешенных математических проблем. Одной из них была задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» — нахождение общего метода, для определения выполнимости данного высказывания на языке формальной логики.

Статья Тьюринга как раз и давала ответ на эту проблему — вторая проблема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки той задачи, по поводу которой она была написана.

Приведем характеристику этой работы, принадлежащую Джону Хопкрофту: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».

Машина Тьюринга является достаточно простым вычислительным устройством. Она состоит из ленты бесконечной длины, разделенной на ячейки, и головки, которая перемещается вдоль ленты и способна читать и записывать символы. Также у машины Тьюринга существует и такая характеристика, как состояние, которое может выражаться целым числом от нуля до некоторой максимальной величины. В зависимости от состояния, машина может выполнить одно из трех действий: записать символ в ячейку, передвинуться на одну ячейку влево или вправо, а также установить внутреннее состояние.

Устройство машины Тьюринга довольно просто, однако на ней можно выполнить практически любую программу. Для выполнения всех этих действий предусмотрена специальная таблица правил, в которой прописано, что нужно делать при различных комбинациях текущих состояний и символов, прочитанных с ленты.

В 1947 году Алан Тьюринг расширил определение, описав «универсальную машину Тьюринга». Позже для решения определенных классов задач была введена ее разновидность, которая позволяла выполнять не одну задачу, а несколько.

Машина Тьюринга может решить любую проблему, которая может быть разбита на элементарные логические шаги, но при наличии достаточного количества времени и памяти. Также важно отметить, что конструкция этой машины не претендует на создание чего-то координально нового.

Алан Мэтисон Тьюринг высказал предположение, которое заключается в следующем: любой алгоритм в интуитивном смысле данного слова может быть представлен эквивалентной машиной Тьюринга. Это предположение более известно как тезис Черча–Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перехода и сравнения к дркгой соседней ячейке, перезаписи ячеек с учетом изменения состояния машины). Следовательно, автомат может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.

§2. Структура и такт работы машины Тьюринга

Машина Тьюринга (МТ) состоит из двух частей – ленты и автомата (см. рис.1):

Лента в машине Тьюринга используется для хранения информации. Она является бесконечной в обе стороны и разбита на клетки, которые никак не именуются и не номеруются. В свою очередь, в каждой клетке может быть записан один символ или же не записано ничего. Содержимое клетки может меняться, то есть в неё можно записать другой символ или стереть находящийся там символ.

Пустое содержимое клетки назовем символом «пусто» и обозначим знаком 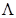(«лямбда»). В связи с этим изображение ленты, показанное на рисунке 1 справа, такое же, как и на рисунке слева. Данное соглашение удобно тем, что операцию стирания символа в некоторой клетке можно рассматривать как запись в эту клетку символа 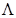, поэтому вместо длинной фразы «записать символ в клетку или стереть находящийся там символ» можно говорить просто «записать символ в клетку».

Автомат является активной частью Машины Тьюринга. В каждый момент он размещается под одной из клеток ленты и видит её содержимое. Такая клетка называется видимой, а находящийся в ней символ – видимым символом. Содержимое же соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний, которые будем обозначать буквой 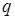номерами .

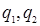Находясь в каком-либо из состояний, автомат выполняет некоторую определённую операцию, например, перемещается направо по ленте, заменяя все символы 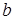на 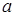, а, в свою очередь, находясь в другом состоянии – другую операцию.

Пару из видимого символа 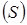и текущего состояния автомата 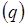будем называть конфигурацией и обозначать .

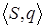Автомат может выполнять три элементарных действия:

1. записывать в видимую клетку новый символ, (то есть менять содержимое других клеток автомат не может);

2. сдвигаться на одну клетку вправо или влево (то есть «перепрыгивать» сразу через несколько клеток автомат не может);

3. переходить в новое состояние.

Никакие другие действия автомат выполнять не умеет, поэтому другие, наиболее сложные операции так или иначе должны сводиться к этим трём элементарным действиям.

Такт работы машины Тьюринга (МТ) работает по шагам (тактами), которые выполняются один за другим. На каждом такте автомат машины Тьюринга выполняет три четко определенных действия, причем обязательно в указанном порядке:

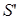
1. записывает некоторый символ в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);

2. сдвигается на одну клетку влево (обозначение – 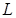, от left), либо на одну клетку вправо (обозначение – 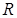, от right), либо остается неподвижным (обозначение – ).

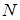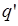
3. переходит в некоторое состояние (в частности, может остаться в прежнем состоянии).

Формально действия одного такта будем записывать в виде тройки: 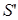, , 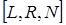, 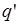где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв 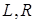или .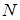

Например, такт 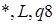*, означает запись символа * в видимую клетку, сдвиг на одну клетку влево и переход в состояние 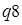. Запись такта для конфигурации называют командой машины Тьюринга.

На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов.

Можно выделить следующие свойства машины Тьюринга как алгоритма:

Машина Тьюринга (МТ) может перейти к ( k +1) шагу только после выполнения каждого шага, так как именно каждый шаг определяет, каким будет, в свою очередь, ( k +1)-й шаг;

На каждом шаге в ячейку записывается один символ, автомат делает одно движение ( L , R , N ), и машина Тьюринга таким образом переходит в одно из описанных состояний;

В каждой ячейке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, то есть, если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же;

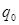
Содержательно результаты всей последовательности шагов и каждого шага определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние , то есть за конечное число шагов будет получен ответ на вопрос задачи;

Каждая машина Тьюринга определена над всеми доступными словами из алфавита, именно в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, то есть для каждой задачи пишется своя, новая машина Тьюринга.

§3. Программа для машины Тьюринга и правила ее выполнения

Машина Тьюринга сама по себе не совершает никаких операций. Для того чтобы увидеть ее работу, необходимо написать программу для данной машины. Эта программа записывается в виде следующей таблицы:

Таблица 1. Программа для МТ.

Источник: znanio.ru