Рассмотрим небольшую задачу, которая обычно предлагается в самом начале практической работы по теме. И такая привилегия не случайна. Для решения типового примера на нахождение суммы ряда не требуется тяжёлый багаж признаков сравнения, признаков Даламбера, Коши и т.д. – достаточно самых минимальных знаний о числовых рядах. Необходимо понимать, что такое ряд , уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
Следует отметить, что в большинстве случаев найти сумму ряда непросто, и этот вопрос обычно решается через функциональные ряды (доживём-доживём:)). Так, например, сумма популярного артиста выводится через ряды Фурье. В этой связи на практике почти всегда требуется установить сам факт сходимости, но не найти конкретное число (многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии , сумма которой легко рассчитывается по известной школьной формуле.
Сходимость по признаку Даламбера и сумма ряда
В данной статье мы продолжим рассматривать похожие примеры, кроме того, узнаем строгое определение суммы и попутно познакомимся с некоторыми свойствами рядов. Разомнёмся… да прямо на прогрессиях и разомнёмся:
Найти сумму ряда
Решение: представим наш ряд в виде суммы двух рядов:
Почему в данном случае так можно сделать? Выполненные действия основаны на двух простейших утверждениях:
1) Если сходятся ряды , то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов: . При этом существенно то обстоятельство, что речь идёт о сходящихся рядах. В нашём примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
2) Второе свойство ещё очевиднее. Константу можно вынести за пределы ряда: , и это не повлияет на его сходимость или расходимость и итоговую сумму. Зачем выносить константу? Да просто чтобы она «не мешалась под ногами». Но иногда бывает выгодно этого и не делать
Чистовое оформление примера выглядит примерно так:
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: , где – первый член прогрессии, – основание прогрессии.
Ответ: сумма ряда
Начало решения можно оформить несколько в другом стиле – расписать ряд напрямую и перегруппировать его члены:
Дальше по накатанной.
Найти сумму ряда
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Каких-либо особых изысков здесь нет, но однажды мне попался необычный ряд , который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно, , и сумма рассчитывается буквально за пару мгновений: .
Математика без Ху%!ни. Вычисление суммы ряда
А сейчас живительный глоток математического анализа, необходимый для решения дальнейших задач:
Что такое сумма ряда?
Строгое определение сходимости/расходимости и суммы ряда в теории даётся через так называемые частичные суммы ряда. Частичные – значит неполные. Распишем частичные суммы числового ряда :
И особую роль играет частичная сумма «эн» членов ряда:
Если предел частичных сумм числового ряда равен конечному числу: , то такой ряд называют сходящимся, а само число – суммой ряда. Если же предел бесконечен либо его не существует, то ряд называют расходящимся.
Вернёмся к демонстрационному ряду и распишем его частичные суммы:
Предел частичных сумм – есть в точности бесконечно убывающая геометрическая прогрессия, сумма которой равна: . Похожий предел мы рассматривали на уроке о числовых последовательностях. Собственно, и сама формула – это прямое следствие вышеизложенных теоретических выкладок (см. 2-ой том матана).
Таким образом, прорисовывается общий алгоритм решения нашей задачи: необходимо составить энную частичную сумму ряда и найти предел . Посмотрим, как это осуществляется на практике:
Вычислить сумму ряда
Решение: на первом шаге нужно разложить общий член ряда в сумму дробей. Используем метод неопределённых коэффициентов:
Сразу же полезно провести обратное действие, выполнив тем самым проверку:
Получен общий член ряда в исходном виде, следовательно, разложение в сумму дробей проведено успешно.
Теперь составим частичную сумму ряда . Вообще это делается устно, но один раз я максимально подробно распишу, что откуда взялось:
Как записать совершенно понятно, но чему равен предыдущий член ? В общий член ряда ВМЕСТО «эн» подставляем :
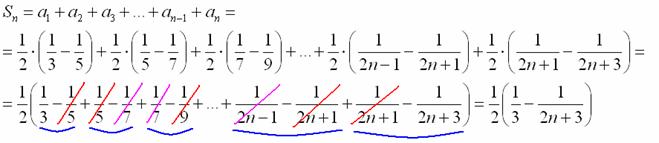
Почти все слагаемые частичной суммы благополучно взаимоуничтожаются:
Прямо такие пометки и делаем карандашом в тетради. Чертовски удобно.
Осталось вычислить элементарный предел и узнать сумму ряда:
Ответ:
Аналогичный ряд для самостоятельного решения:
Вычислить сумму ряда
Примерный образец чистового оформления решения в конце урока.
Очевидно, что нахождение суммы ряда – это само по себе доказательство его сходимости (помимо признаков сравнения, Даламбера, Коши и др.), о чём, в частности, намекает формулировка следующего задания:
Найти сумму ряда или установить его расходимость
По внешнему виду общего члена можно сразу сказать, как ведёт себя этот товарищ. Без комплексов. С помощью предельного признака сравнения легко выяснить (причём даже устно), что данный ряд будет сходиться вместе с рядом . Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.
Решение: разложим знаменатель дроби в произведение. Для этого нужно решить квадратное уравнение:
Множители лучше расположить в порядке возрастания: .
Выполним промежуточную проверку:
Таким образом, общий член ряда:
Коэффициенты получились целые и это радует:
На всякий случай выполним ещё одну промежуточную проверку:
Поэтапные проверки – королевы зачётов 😉
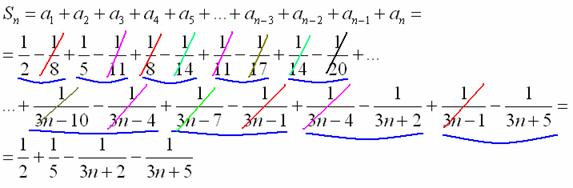
Составим энную частичную сумму и уничтожим всё, что можно уничтожить:
Как видите, в этот раз противоположные числа не расположены рядышком. Поэтому на практике всегда лучше перестраховаться и записать побольше членов ряда – чтобы наверняка понять, какие слагаемые исчезнут, а какие – нет. По той же причине крайне желательно выполнять пометки карандашом.
Опыт показывает, что чаще всего студенты испытывают затруднения с хвостом суммы. В этой связи ещё раз повторим принцип, по которому записаны члены . Отчего ж не повторить?
В общий член ряда :
– ВМЕСТО «эн» подставляем : ;
– ВМЕСТО «эн» подставляем : ;
– ВМЕСТО «эн» подставляем : .
На завершающем этапе находим сумму ряда:
Ответ:
Изящный ряд для самостоятельного решения:
Найти сумму ряда или установить его расходимость
Решение и ответ в конце урока.
Вероятно, на этом рубеже у многих посетителей возникла уверенность в своих навыках и желание раствориться на просторах Интернета. Рекомендую немного задержаться, поскольку ниже по течению среди, казалось бы, такого однообразия приветливо моргают глазами большие крокодилы.
Усложняем задание и набиваем руку:
Вычислить сумму ряда
Решение: со знаменателем тут никаких проблем:
Множители, как я уже отмечал, целесообразно расположить в порядке возрастания.
Здесь на последних шагах проведено почленное сложение двух уравнений системы.
Что и требовалось проверить.
Запишем частичную сумму «эн» членов ряда, при этом обращаем внимание на тот факт, что «счётчик» ряда «начинает работать» с номера . Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:
Однако если мы запишем в одну-две строчки, то всё равно будет довольно трудно сориентироваться в слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:
Да, прямо так и пишем в тетради один член под другим и прямо так их вычёркиваем. Кстати, собственное изобретение. Как понимаете, не от самого лёгкого задания в этой жизни =)
В результате зачистки получаем:
И, наконец, сумма ряда:
Ответ:
Вычислить сумму ряда
Это пример для самостоятельного решения.
Рассматриваемая задача, конечно, не радует нас разнообразием – на практике встречается либо бесконечно убывающая геометрическая прогрессия, либо ряд с дробно-рациональным общим членом и разложимым многочленом в знаменателе (к слову, далеко не каждый такой многочлен даёт возможность найти сумму ряда). Но, тем не менее, иногда попадаются необычные экземпляры, и по сложившейся доброй традиции я завершаю урок какой-нибудь любопытной задачей:
Вычислить сумму ряда, если она существует
Решение: формулировка уже интригует. Интересен тот факт, что все члены данного ряда отрицательны. Почему? На интервале логарифм меньше нуля, а за счёт аргумента при любом натуральном «эн» (начиная с ) мы каждый раз и попадаем в этот интервал.
Таким образом, если ряд сходится, то будет отрицательна и его сумма. Только вот есть мааааленькая проблемка – найти это значение, если оно существует =)
Алгоритм такой же, главное, догадаться, с какой стороны подступиться к решению. Предыдущий опыт подсказывает, что нужно попытаться представить общий член ряда в виде суммы двух или бОльшего количества слагаемых. Из этих соображений преобразуем выражение в скобках и используем свойства логарифма:
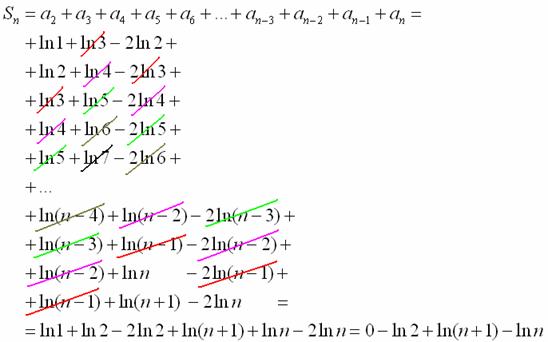
Ну что же, выглядит вполне перспективно, давайте разберёмся с частичной суммой ряда:
В целях устранения неопределённости вновь используем свойство логарифма:
Получено конечное число, а значит, ряд сходится. Как и ожидалось, сумма получилась отрицательной.
Ответ:
Поздравляю со знаменательным событием! Коль скоро вы читаете эти строки, то сегодня на вашу долю выпал редкий и счастливый случай – когда в частичной сумме ряда удалось массово ликвидировать слагаемые. Удалось же? =)
Не каждый день бывает! Но то ли ещё будет 😉
Решения и ответы:
Пример 2: Решение:
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: .
Для первого ряда: , для второго ряда: .
Ответ: сумма ряда
Пример 4: Решение: Методом неопределенных коэффициентов разложим общий член ряда в сумму дробей:
Таким образом:
Найдём частичную сумму ряда:
Вычислим сумму ряда:
Ответ:
Пример 6: Решение: разложим знаменатель общего члена в произведение и методом неопределённых коэффициентов получим сумму дробей:
Таким образом:
Составим частичную сумму и проведём упрощения:
Вычислим сумму ряда:
Ответ:
Пример 8: Решение: представим общий член ряда в виде:
Методом неопределённых коэффициентов разложим его в сумму дробей:
Таким образом:
Запишем частичную сумму:
Вычислим сумму ряда:
Ответ:
(Переход на главную страницу)
Contented.ru – онлайн школа дизайна
SkillFactory – получи востребованную IT профессию!
Источник: www.mathprofi.ru
Лабораторная работа №3. Программирование циклических алгоритмов
Закрепить практические навыки работы с системой PascalABC.net, научиться правильно использовать различные операторы циклов; научиться составлять программы решения задач с использованием циклических структур.
Общие сведения
Алгоритм называется циклическим, если он содержит многократное выполнение одних и тех же операторов при различных значениях промежуточных данных. Число повторений этих операторов может быть задано в явной (цикл с известным заранее числом повторений) или неявной (цикл с неизвестным заранее числом повторений) форме.
Примеры решения задач по теме «Программирование циклических алгоритмов»
Задание 1
Для организации вычислений суммы и произведения использовать оператор цикла с параметром For.
Этапы решения задачи
1. Для упрощения расчетов разобьем выражение на две составляющие:
Окончательное значение y вычислим по формуле
2. Составляем блок-схему алгоритма и программу расчета, используя оператор цикла for
 |
4. Выполним программу в среде Pascal ABC.NET (см. п.3.1.4).
Задание 2
Написать программу для вычисления приведенной ниже функции
с использованием операторов:
c) Repeat…until.
Этапы решения задачи
1. Определим переменные, которые будем использовать в программе:
S – сумма ряда, b – степень числителя x, a – степень очередного слагаемого в знаменателе, z –знак слагаемого.
2. Для вычисления N – числа повторений цикла for.. –используем формулу
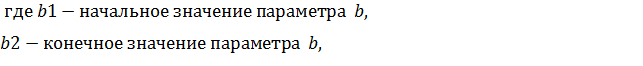
3. Составляем блок-схему алгоритма и программу расчета, используя оператор цикла for
 |
PROGRAM ZADANIE2_a; Var b, S, x, b1, b2, h: real; a, i, z, n: integer; Begin Z: = 1; А: = 2; x:=0.73; B: = 1.2; B1: = B; B2: = 4.2; H:=0.2; N:=trunc((B2 -B1)/h)+1; For I: = 1 То N do Begin S: = S+ z *(sin(exp(b* ln(x))) /exp(a*ln(2))); a: = а + 2; b: = b+H; z:= – z; End; Writeln(‘ Сумма =’, S:6:4); End. |
4. Составляем блок-схему алгоритма и программу расчета, используя оператор цикла while..do. Этот цикл называется циклом с предусловием, так как проверка проводится до начала очередной итерации. До первого входа в цикл переменной b уже должно быть присвоено начальное значение. Затем сравним его с конечным значением. Цикл будет выполняться, пока условие истинно.
Как только условие нарушается, выполнение цикла завершается.
 |
5. Составляем блок-схему алгоритма и программу расчета, используя оператор цикла Repeat…until.
 |
PROGRAM ZADANIE2_С; Var b, S, x, h: real; a, i, z, n: integer; Begin Z: = 1; x:=0.73; А: = 2; S:= 0; B: = 1.2; H:=0.2; repeat S: = S+ z *(sin(exp(b* ln(x))) /exp(a*ln(2))); a: = а + 2; b: = b+H; z:= – z; until (b>4.2); Writeln(‘ Сумма =’, S:6:4); End. |
3. Выполним программу в среде Pascal ABC.NET (см. п.3.1.4).
Задание 3
Составить программу, которая вычисляет сумму ряда с заданной точностью. Нужная точность считается полученной, если очередное слагаемое оказалось по модулю меньше, чем данное малое положительное число e.
. х =1,7, e=10 –3 .
Этапы решения задачи
1. Определим переменные, которые будем использовать в программе: S – сумма ряда, SL – текущее слагаемое, F – знаменатель(факториал), eps – заданная точность, N – номер слагаемого. По условию задачи слагаемое требуется сравнивать с заданной точностью. Наиболее удобным для данного вида вычислений является оператор цикла Repeat…until, так как проверка условия осуществляется после каждого выполнения тела цикла.
2. Составим блок-схему алгоритма и программу расчета.
 |
4. Выполним программу в среде Pascal ABC.NET (см. п.3.1.4).
Задание 4
Затабулировать функцию двух переменных 
внутри квадрата 
и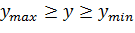 
и области существования функции 
. Шаги табуляции Δ х = Δ у. Результаты вывести в виде таблицы. В точках, где функция не определена, вывести 4 символа «*».
 |
x | y | Δ х = Δ y |
 |
[-1; 2] | [0; 1] | 0,1 |
Этапы решения задачи
1. 
Для вычисления функции 
определим область допустимых значений функции: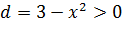 
, так как «подкоренное» выражение должно быть положительным.
2. Так как функция зависит от двух переменных 
, будем использовать конструкцию из вложенных циклов while..do. Составим блок-схему алгоритма и программу расчета.
Program zadanie4;
var Z, x, Y:real;
WRITELN(‘ | N | X | Y | Z |’);
writeln(‘__________________________’);
writeln(‘__________________________‘);
Варианты заданий по теме «Циклические алгоритмы»
Задание 1
Вычислить значение функции y. Значение x задать произвольно.
| № варианта | Значение y |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
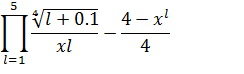Задание 2
Написать программу для вычисления значения функции F (x) с использованием операторов: For…; While…do; Repeat…until. Значение x задать произвольно.
| № варианта | Вид выражения F(x) |
 . |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
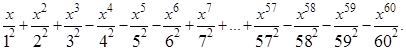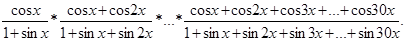 N ввести с клавиатуры |
|
 |
|
 |
|
 |
|
 |
Задание 3
Составить программу, которая вычисляет сумму ряда с заданной точностью. Нужная точность считается полученной, если очередное слагаемое оказалось по модулю меньше, чем e (это и все последующие слагаемые учитывать не надо).
| № вар-та | Вид выражения | х | Точность e |
 |
1,25 | 10 –4 | |
 |
1,7 | 10 –3 | |
 |
1,1 | 0,5×10 –4 | |
 |
– | 0,5×10 –4 | |
 |
0,35 | 10 –3 | |
 |
0,7 | 10 –4 | |
 |
0,3 | 10 –4 | |
 |
0,15 | 10 –4 | |
 |
0,21 | 10 –3 | |
 |
0,15 | 10 –4 | |
 |
0,3 | 0,5×10 –4 | |
 |
0,15 | 10 –4 | |
 |
0,7 | 10 –4 | |
 |
0,1 | 0,5×10 –4 | |
 |
– | 10 –3 |
Задание 4
Затабулировать функцию двух переменных внутри квадрата и 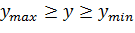и области существования функции . Шаги табуляции Δ х = Δ у. Результаты вывести в виде таблицы. В точках, где функция не определена вывести 4 символа «*».
| № варианта |  |
x | y | Δ х = Δ y |
 |
[0; 1] | [0; 1] | 0,1 | |
 |
[0; 2] | [0; 2] | 0,2 | |
 |
[0; 1] | [0; 1] | 0,1 | |
 |
[0; 2] | [0; 2] | 0,2 | |
 |
[0; 1,5] | [0; 1,5] | 0,15 | |
 |
[0; 1] | [0; 1] | 0,1 | |
 |
[0; 3] | [0; 3] | 0,3 | |
 |
[0; 1,5] | [0; 1,5] | 0,15 | |
 |
[0; 2] | [0; 2] | 0,2 | |
 |
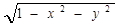[0; 1] | [0; 1] | 0,1 | |
 |
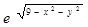[0; 4] | [0; 4] | 0,4 | |
 |
[0; 1] | [0; 1] | 0,3 | |
 |
[-1; 1] | [0; 1] | 0,1 | |
 |
[0; 1] | [-1,2; 1,2] | 0,2 | |
 |
[0; 1,5] | [0; 1,5] | 0,15 |
Лабораторная работа №4.
Источник: megalektsii.ru
Лабораторная работа № 3
Тема: Вычисление сумм (произведений) конечного числа элементов ряда. Оператор FOR …DO (FOR . DOWNTO)
Цель работы: научиться разрабатывать блок-схему алгоритма и программу с использованием операторов цикла FOR …DO на примере вычисления сумм (произведений) элементов конечного ряда
Теоретическая часть
Оператор FOR …DO
Циклические вычисления в Паскале реализуются с помощью операторов FOR. TO(DOWNTO). DO, WHILE. DO или REPEAT. UNTIL.
Особенностью операторов FOR. TO (DOWNTO). DO является встроенный внутренний счетчик цикла, фиксирующий количество повторений.
Форматы записи оператора:
FOR переменная цикла := выражение 1 TO выражение 2 DO
FOR переменная цикла :=выражение 1 DOWNTO выражение 2 DO
В формате: переменная цикла (управляющая переменная, счетчик цикла) – имя переменной целочисленного типа; выражения 1 и 2 — выражения, тип результата которых совпадает с типом переменной цикла; операторы тела цикла — любой исполнимый оператор или блок операторов, заключенных в операторные скобки; FOR, TO, DOWNTO и DO – ключевые слова.
. Использование оператора FOR регламентируется следующими правилами.
- Переменная цикла, её начальное и конечное значения должны быть одного типа.
- При выполнении оператора очередное значение параметра цикла вычисляется автоматически. В частности, для целого типа шаг изменения значения переменной цикла равен 1 при конструкции с TO и -1 при конструкции с DOWNTO.
- После служебного слова DO может стоять только один оператор. Если в цикле необходимо выполнить группу операторов, то их заключают в операторные скобки BEGIN. END, образуя составной оператор.
- Цикл не выполняется вообще, если начальное значение переменной цикла больше (при DOWNTO меньше), чем конечное. В этом случае управление передается оператору, следующему непосредственно за конструкцией FOR..TO(DOWNTO). DO.
- В конструкции FOR..TO(DOWNTO). DO используется только одна переменная цикла. При наличии вложенных циклов у каждой конструкции FOR..TO(DOWNTO). DO должна быть своя, отличающаяся от других переменная.
- При организации вложенных циклов внутренний и внешний циклы не должны пересекаться. Цикл, который начинается последним, должен завершаться первым:
FOR N := 1 TO 5 DO
BEGIN WRITELN (N:2,’.’);
FOR J := 1 TO 5 DO WRITELN (N:2,’.’, J:2,’.’) END;
Пример работы циклов
Пример 3.1. Найти сумму конечного ряда. Значение x вводится с клавиатуры.
var x,s:real; i:integer;
for i:=1 to 10 do //начало цикла For
s:=s+x*i; //конец цикла For
Writeln(‘s=’,s:5:3); //вывод результата
Пример 3.2. Дано действительное число х. Вычислить сумму элементов ряда. Число суммируемых элементов ряда (N) задается во время работы программы с клавиатуры.
Program Project2; //вычисление суммы заданного числа элементов ряда
begin //начало раздела операторов
write(‘введите значение x=’);
write(‘введите значение n=’);
//значение первого слагаемого ряда вычисляется до цикла
a:=x; //значение x в степени (2*1-1)
f:=1; //значение f=(2*1-1)!=1
s:=a; //а — значение 1-го слагаемого, s=a
//к — переменная для изменения знака очередного слагаемого с + на —
for i:=2 to n do //начало цикла
k:=- k; //значение (-1) для i-го слагаемого
a:=a * sqr(x); //вычисление х в степени (2i+1) i-го слагаемого
f:=f * (2*i-2)*(2*i-1); //вычисление факториала i-го слагаемого
s:=s+k*a/f; //добавление i-го слагаемого к общей сумме
end; //конец цикла
//вывод результата на экран
writeln(‘при x=’,x:4:2,’ сумма’, n,’ элементов =’,s:7:5);
Пример 3.3. Задано число х и натуральное число N. Вычислить произведение N элементов ряда
Для вычисления произведения целесообразно использовать рекуррентные соотношения, т.е. каждую дробь в скобках, начиная со второй, выражать через предыдущую. Это позволит существенно сократить объем вычислений. Расчет N! в числителе дроби каждого множителя выполняется в программе в теле цикла по формуле f:=f*n. p:=p*(2+f/a) — формула умножения элементов ряда Р=P1*P2*…*Pi-1 на очередной Pi элемент ряда.
Схема алгоритма и текст программы
//вычисление произведения заданного числа элементов ряда
x,p,a : real; f : longint; i,n : integer;
p:=1; //начальное значение произведения
a:=1; f:=1; //начальные значение числителя и знаменателя дроби
for i:=1 to n do //начало цикла
end; //конец цикла
//вывод результата на экран
writeln(‘при x=’,x:4:2,’ произведение’, n:2,’ элементов=’,p:7:5);
Задания для лабораторной работы
1. С клавиатуры вводится последовательность из n-чисел. Определить количество членов последовательности:
- являющихся нечетными числами;
- кратных 3 и не кратных 5;
- являющихся квадратами четных чисел.
2. Последовательность чисел Фибоначчи u0, u1, … образуется по закону u0=0; u1 =1; ui=ui-1+ui-2 (i=2, 3, …). Дано натуральное число n>1.
3. С клавиатуры вводится натуральное число n, действительные числа а1, … ,an. В последовательности а1, … ,an определить число соседств:
- двух положительных чисел;
- двух чисел разного знака;
- двух чисел одного знака, причем модуль первого числа должен быть больше модуля второго числа.
4. У прилавка в магазине выстроилась очередь из n покупателей. Время обслуживания продавцом i-го покупателя равно ti (i=1, … ,n). Пусть даны натуральное число n и действительные t1, … ,tn.
Получить c1, … ,cn , где ci – время пребывания i-го покупателя в очереди (i=1, … ,n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
5. Даны действительные числа a, b (ab), натуральное число n, функция y=f(x), определенная на отрезке [a, b]. Для значений аргумента xi = a+ih (i=0,1, … ,n), h=(b-a)/n вычислить значения функции yi = f( xi ) (i=0,1, … ,n).
Вывести xi и yi (i=0,1, … ,n) в виде таблицы из двух колонок. В i-ю строку таблицы заносятся соответствующие значения xi и yi. Рассмотреть следующие функции:
- , a= –π, b=π, n=50;
- , a= 0, b=2π, n=50;
- , a= –3, b=5, n=40;
- , a= –1, b=2, n=30;
- , a= –1, b=3, n=40.
Задания для самостоятельного выполнения
Варианты заданий в табл. 1, 2.
Вычислить значение суммы или произведения членов ряда. Значение x задать с клавиатуры.
Источник: studfile.net