Соотношение программы и алгоритма

Разработка алгоритмов и программ для решения дифференциальных уравнений численными методами

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).

Рассмотрим два варианта вывода расчетных формул

Решение обыкновенных дифференциальных уравнений. Разработка алгоритмов и проектировка программного обеспечение для численного решения обыкновенных дифференциальных уравнений

Страницы работы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информационные технологии»

ЛАБОРАТОРНАЯ РАБОТА №4

Расширенный алгоритм евклида

по дисциплине: «ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ»

Решение обыкновенных дифференциальных уравнений

Выполнил: студент гр. ИТ-31

Лабораторная работа №4

«Решение обыкновенных дифференциальных уравнений»

Цель работы: научиться разрабатывать алгоритмы и проектировать программное обеспечение для численного решения обыкновенных дифференциальных уравнений.

Разработать алгоритм и написать программу, реализующую численного решение обыкновенных дифференциальных уравнений следующими методами.

// ConsoleApplication2.cpp: определяет точку входа для консольного приложения.

Численное решение математических моделей объектов заданных системами дифференциальных уравнений

Введение:

При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.

Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.

Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.

В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.

Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).

Какая программа быстрее? Вычислительная сложность алгоритма.

Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ

Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:

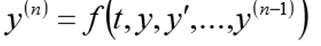
и начальным условиям

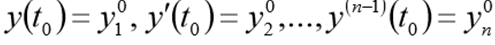
Перед решением эта задача должна быть переписана в виде следующей СДУ

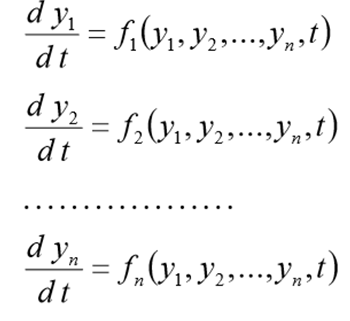
(1)

с начальными условиями

Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.

Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.

Функция func должна возвращать список из n значений функций при заданном значении независимого аргумента t. Фактически функция func(y,t) реализует вычисление правых частей системы (1).

Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений при t=t0.

Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.

Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле

Они могут быть векторами или скалярами. По умолчанию

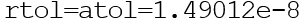
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.

Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

При численном решении задачи Коши

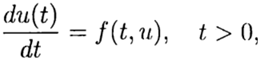
(2)

(3)

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.

Приближенное решение задачи (2), (3) в точке 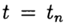обозначим . Метод сходится в точке 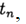если при . Метод имеет р-й порядок точности, если 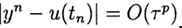, р > 0 при . Простейшая разностная схема для приближенного решения задачи (2),(3) есть

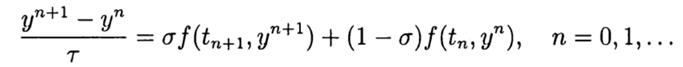
(4)

При 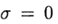имеем явный метод и в этом случае разностная схема аппроксимирует уравнение (2) с первым порядком. Симметричная схема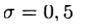

в (4) имеет второй порядок аппроксимации. Эта схема относится к классу неявных — для определения приближенного решения на новом слое необходимо решать нелинейную задачу.

Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема

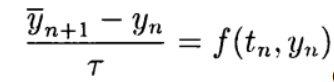
(5)

а на этапе корректора (уточнения) — схема

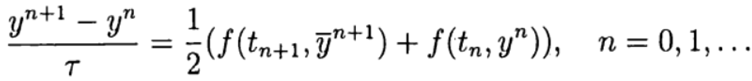
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

(6),

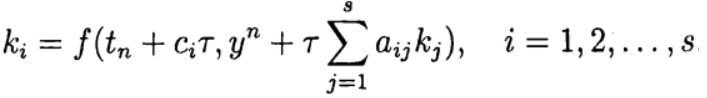
Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если при 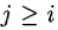имеем явный метод Рунге—Кутта. Если при j>1 и 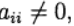то определяется неявно из уравнения:

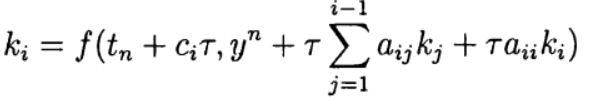
(7)

О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры определяют вариант метода Рунге—Кутта. Используется следующее представление метода (таблица Бутчера)

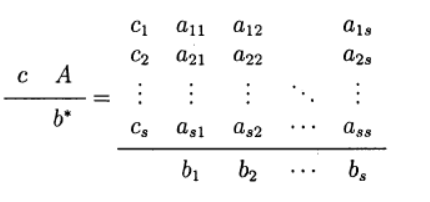
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

(8)

Метод Рунге—Кутта— Фельберга

Привожу значение расчётных коэффициентов метода

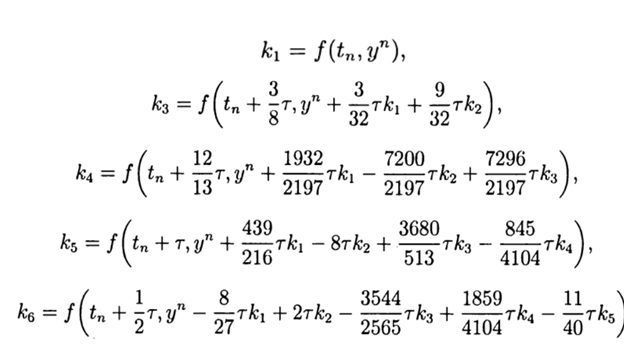
(9)

С учётом(9) общее решение имеет вид:

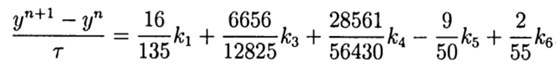
(10)

Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.

Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения 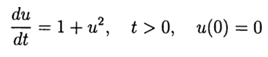с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга

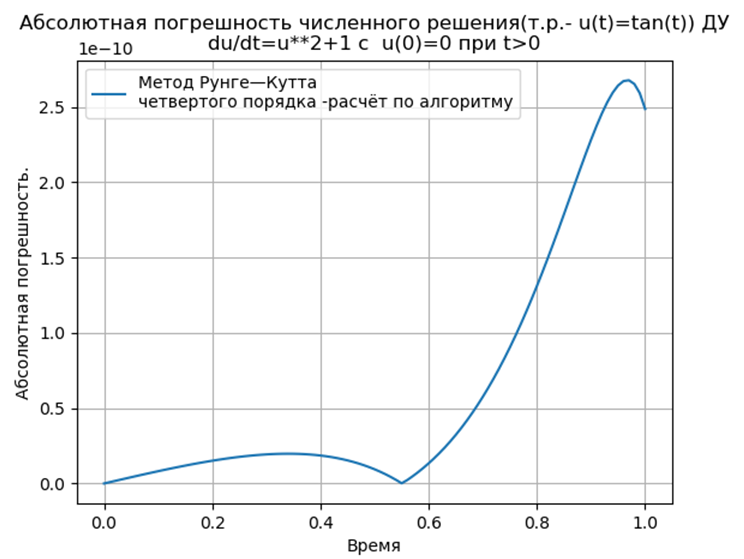
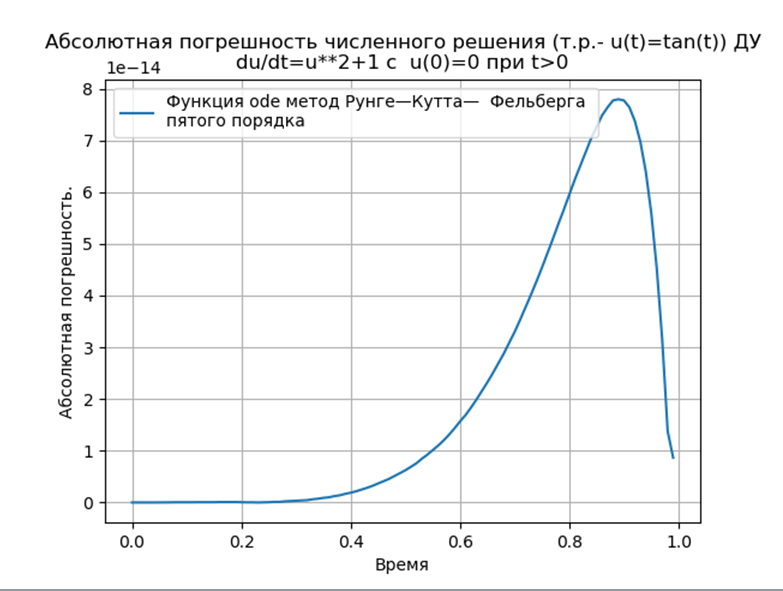
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.

Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга

Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].

Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид

где – радиус вектор движущегося тела, – вектор скорости тела, – коэффициент сопротивления, вектор силы веса тела массы m, g – ускорение свободного падения.

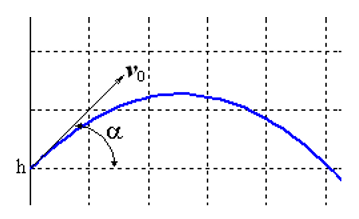
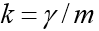
Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить , то в координатной форме мы имеем систему уравнений:

К системе следует добавить начальные условия: (h начальная высота), . Положим 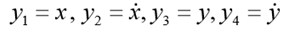. Тогда соответствующая система ОДУ 1 – го порядка примет вид:

Для модельной задачи положим . Опуская довольно обширное описание программы, приведу только листинг из комментариев к которому, думаю, будет ясен принцип её работы. В программу добавлен отсчёт времени работы для сравнительного анализа.

Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787

Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:

Время на модельную задачу: 0.259927

Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.

Решение краевой задачи с поточно разделёнными краевыми условиями

Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:

(11)

Для решения задачи (11) используем следующий алгоритм:

1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями

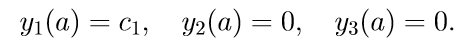
Введем обозначение для решения задачи Коши:

2. Решаем первые три однородные уравнения системы (11) с начальными условиями

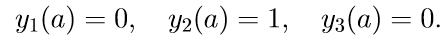
Введем обозначение для решения задачи Коши: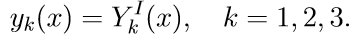

3. Решаем первые три однородные уравнения системы (11) с начальными условиями

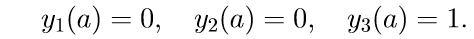
Введем обозначение для решения задачи Коши:

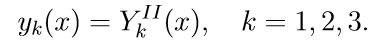
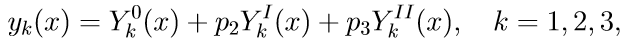
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений:

где p2, p3 — некоторые неизвестные параметры.

5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:
(12)
Решая (12), получим соотношения для p2, p3.

По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:

y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878

Вывод

Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.

3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.

Источник: all-equa.ru

Алгоритмы, величины, структура алгоритмов

На этом уроке закрепляется ранее изученный материал. Рассказывается, что такое алгоритм, какие бывают данные и величины; рассматриваются разновидности типов данных и их основные отличия; изучается структура алгоритмов, а такжебазовые способы их записи, такие как следование, ветвление и цикл.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.

Получите невероятные возможности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ

Конспект урока «Алгоритмы, величины, структура алгоритмов»

На этом уроке мы с вами закрепим ранее изученный вами материал. Вспомним, что такое алгоритм, какие бывают величины, а также разберёмся со структурой алгоритмов.

Начнём мы с вами с этапов решения задач. Всего их шесть:

1. Постановка задачи.

2. Формализация задачи.

3. Построение алгоритма.

4. Составление программы на языке программирования.

5. Отладка и тестирование программы.

6. Проведение расчётов и анализ полученных результатов.

Но к программированию из этого списка относятся только пункты 3-5.

Давайте разберёмся, что происходит на каждом этапе решения задачи.

Итак, на первом этапе – постановка задачи, нужно понять условие задачи, выделить исходные данные и данные, которые требуется получить в результате, и понять отношения между ними.

Второй этап – формализация задачи. На этом этапе задача чаще всего переводится на математический язык. То есть строится математическая модель.

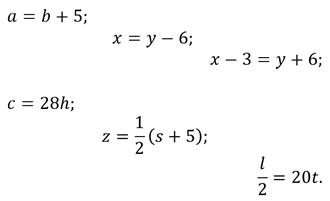
Далее идёт этап построения алгоритма. На данном этапе нужно записать решение задачи в виде, например, блок-схемы.

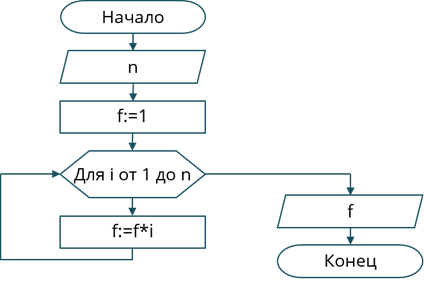
На четвёртом этапе идёт уже работа с компьютером. То есть здесь мы будем записывать задачу на языке программирования, в нашем случае на языке Паскаль.

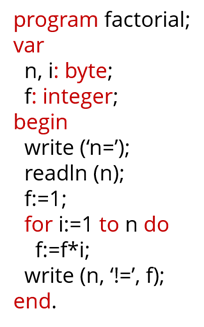
На этапе тестирования и отладки проверяется, работает ли программа. И если работает, то правильно ли. Также выявляется наличие либо отсутствие ошибок в программе.

И на последнем этапе проводятся расчёты и анализ полученных результатов. То есть используется разработанная программа в практических целях.

Но, при решении задач по программированию на занятиях, учащиеся обычно заканчивают работу на 5 этапе.

Исходя из этапов решения задач, можно сделать вывод, что программист должен уметь строить алгоритмы, знать языки программирования, а также уметь работать в соответствующей системе программирования. В основе всей работы лежит развитое алгоритмическое мышление.

А сейчас обратимся немного к истории появления такого понятия, как «алгоритм».

Происхождение термина «алгоритм» связано с математикой. История его возникновения такова.

В IX веке в Багдаде жил учёный Абу Аль-Хорезми, математик, астроном, географ.

В одном из своих трудов он описал десятичную систему счисления и впервые сформулировал правила выполнения арифметических действий над целыми числами и обыкновенными дробями.

Арабский оригинал этой книги был утерян, но остался латинский перевод XII века, по которому Западная Европа ознакомилась с десятичной системой счисления и правилами выполнения арифметических действий.

Первыми алгоритмами в математике являются сложение, вычитание, умножение «столбиком», деление «уголком» многозначных чисел.

Многие столетия разрабатывались алгоритмы для решения всё новых и новых классов задач, но само понятие алгоритма не имело точного математического определения.

В наше же время, алгоритм – это последовательность команд управления каким-либо исполнителем. С понятием алгоритма и методами его построения учащиеся знакомятся на примере таких исполнителей, как Робот, Черепашки, Чертёжник и другими.

Также существует графический исполнитель, с помощью которого можно создавать рисунки на экране, осуществлять перемещение в лабиринтах, перемещать предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке.

При выполнении какой-либо программы исполнитель работает с величинами – различными информационными объектами. К таким объектам относятся числа, символы, коды и так далее. Таким образом, алгоритмы работы с величинами – это алгоритмы, предназначенные для управления компьютером.

А сейчас рассмотрим более подробно данные и величины.

Данные – это совокупность величин, с которыми работает компьютер.

Данные делятся на исходные, результаты и промежуточные данные. Исходные данные – это данные, которые заданы изначально, по условию. Промежуточные данные – это данные, которые получаются в процессе вычислений. Результаты – это данные, которые являются окончательным ответом на поставленную задачу. То есть мы вводим в программу исходные данные.

Затем исполнитель (компьютер) выполняет действия, описанные в программе, в результате чего получаются промежуточные данные. А после выполнения всех команд программы, компьютер получает и выдаёт нам результаты.

Например, при нахождении площади треугольника через полупериметр, исходными данными будут являться стороны a, b, c. К промежуточным данным будет относится нахождение полупериметра. А результатом – площадь треугольника.

Необходимо помнить следующее правило: всякая величина занимает своё определённое место в памяти компьютера. Мы с вами знаем, что память компьютера можно представить в виде таблицы, которая состоит из ячеек. То есть всякая величина занимает определённую ячейку в памяти компьютера.

Любая величина имеет три основных свойства: имя, значение и тип. Процессор же различает величины по адресу ячеек памяти, в которых они хранятся.

Величины делятся на константы и переменные. Константа – это неизменная величина, которая представляется в алгоритме собственным значением. Её значение в течение всей программы не изменяется, то есть оно постоянно.

Переменная же может изменять своё значение. Например, в начале программы она была равна 3, а в конце – 10.

Любая константа или переменная занимают ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке.

А сейчас перейдём к типам данных.

К основным типам данных относятся целый, вещественный, логический и символьный типы. Типы данных различаются между собой по трём критериям: множество допустимых значение, множество допустимых операций, форма внутреннего представления. Все эти свойства предоставлены в таблице на экране.

Типы констант определяются по форме записи в тексте.

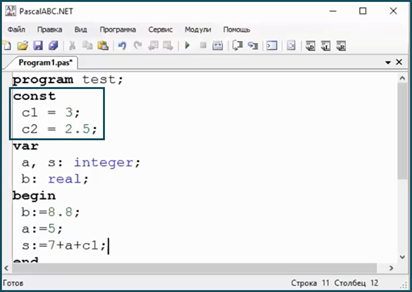
А типы переменных задаются в разделе описания переменных.

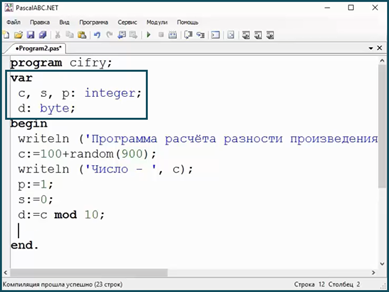
Данные также можно классифицировать по структуре. Они делятся на простые и структурированные. Простые величины имеют одно значение, а вот структурированные – множество. К структурированным величинам относятся массивы, строки и так далее.

В нашем конкретном случае при написании программы исполнителем является компьютер. А если разбираться более подробно, то исполнителем является комплекс: компьютер плюс система программирования.

Таким образом программист будет составлять программу на том языке, на который ориентирована система программирования. В нашем случае, мы будем составлять программы на языке Pascal.

Тем не менее, независимо от того, на каком языке программирования будет написана программа, алгоритм решения любой задачи на компьютере может быть составлен из следующих команд:

· обращение к вспомогательному алгоритму (подпрограмме);

Для описания алгоритмов лучше всего использовать блок-схемы.

В 1969 году известный голландский учёный-программист Эдсгер Вибе Дейкстра доказал следующее: алгоритм для решения любой логической задачи можно составить только из структур «следование», «ветвление», «цикл». Такие структуры называются базовыми алгоритмическими структурами.

Методика программирования, основанная на этой теореме, называется структурным программированием.

Для описания структур алгоритмов можно использовать два способа: блок-схемы и учебный Алгоритмический язык.

Давайте ещё раз рассмотрим базовые алгоритмические структуры и способы их записи.

Следование – это линейная последовательность действий.

В данном случае, серия – это простой или составной оператор. Составной оператор – это серия, заключённая в операторные скобки. В языке Паскаль: begin…end.

Далее рассмотрим ветвление. Ветвление – это алгоритмическая альтернатива. Рассмотрим блок-схему полного ветвления.

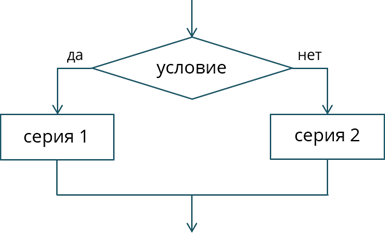
Если заданное условие выполняется, то управление передаётся серии 1, а если нет – серии 2. Полное ветвление, записанное на алгоритмическом языке:

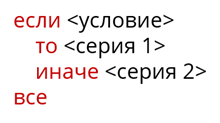
Условие – это утверждение, которое может быть истинным или ложным. Такое утверждение также называют логическим выражением.

Также для записи можно использовать неполную форму ветвления.

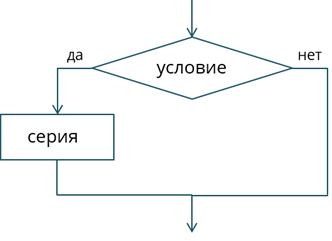
В ней, если условие выполняется, управление передаётся серии, а если нет, то программа переходит к выполнению остальных команд, следующих за ветвлением.

Цикл – это повторение некоторой группы действий по условию. Существуют два типа цикла: цикл с предусловием (цикл-пока), цикл с постусловием (цикл-до).

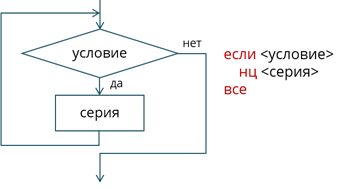
При цикле с предусловием, серия будет выполняться до тех пор, пока условие истинно. То есть сначала идёт проверка условия, а затем решается, будет выполняться серия или нет. При использовании данного цикла серия может ни разу не выполниться, так как условие может быть ложно.

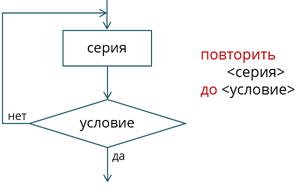
А при цикле с постусловием сначала идёт серия, а затем условие. Серия будет выполняться до тех пор, пока условие ложно. В данном цикле серия выполнится хотя бы один раз, прежде чем программа приступит к проверке условия.

До этого мы с вами рассматривали базовые структуры. Сложный же алгоритм состоит из соединённых между собой базовых структур. Между собой эти структуры могут соединяться двумя способами: последовательным и вложенным.

Если блок, который составляет тело цикла сам по себе является циклической структурой, то это будет являться вложенным циклом.

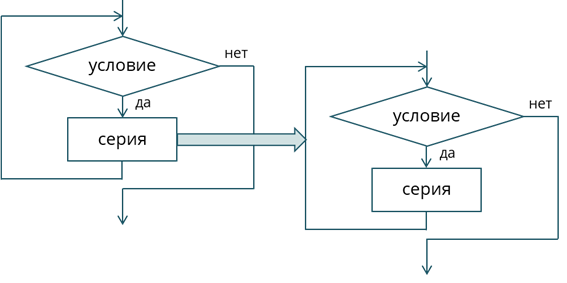
Внутренний цикл также может иметь в себе ещё один цикл и так далее. Таким образом появляется представление о глубине вложенности циклов.

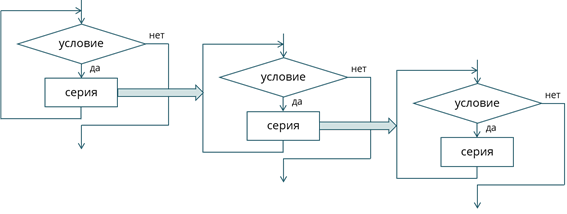
Таким же образом и ветвления могут быть вложенными друг в друга.

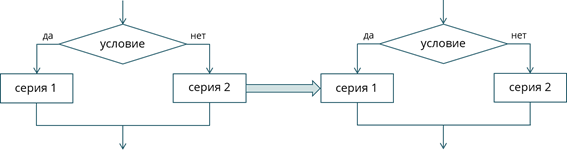
При изображении блок-схем вложенных циклов или ветвлений нужно соблюдать некоторые правила.

Давайте рассмотрим их на примере. На данной схеме «у» – условие, «с» – серия, «+» – да, «–» – нет.

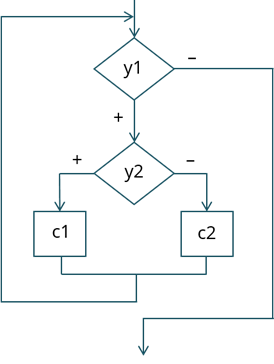
Каждая базовая структура должна иметь один вход и один выход. Чертить их нужно при помощи таких же элементов, как и ранее, в обратном случае нестандартно изображённая блок-схема будет плохо читаться и будет теряться наглядность алгоритма.

Наша же блок-схема легко читается, а структура хорошо воспринимается визуально. У нас изображён цикл с вложенным ветвлением.

Рассмотрим ещё одну блок-схему.

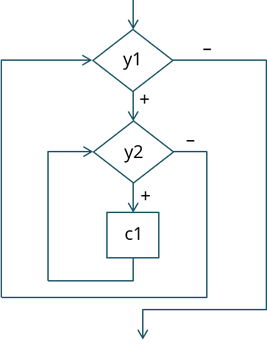
На ней изображены вложенные циклы-пока. Глубина вложенности – 1.

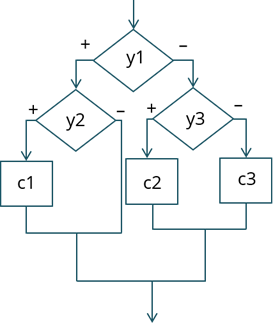
На третьей схеме изображены вложенные ветвления. Глубина вложенности – 1.

При описании алгоритма на алгоритмическом языке нужно структурировать внешний вид текста. Для этого также существуют свои правила:

· конструкции одного уровня вложенности записываются на одном вертикальном уровне (начинаются с одной позиции в строке);

· вложенная конструкция записывается смещённой по строке на несколько позиций вправо относительно внешней для неё конструкции.

Всё это вы можете увидеть при записи приведённых выше блок-схем на алгоритмическом языке.

Такой же способ используется и при структуризации текста в программе языка Паскаль.

Структурное программирование – это не только форма описания алгоритма и программы, но это ещё и способ мышления программиста. При размышлении над составлением алгоритма, необходимо представлять его при помощи стандартных структур. То есть складывать сложную программу из простых частей.

А сейчас подведём итоги урока.

Существует шесть этапов решения задачи на компьютере.

Исполнителем алгоритмов обработки данных являются компьютер и система программирования.

Данные можно классифицировать по нескольким критериям: по отношению к алгоритму, по значениям, по типам и по структуре.

К базовым алгоритмическим структурам относятся следование, ветвление, цикл.

Соединять базовые структуры можно двумя способами: последовательным и вложенным.

При составлении блок-схем или записи алгоритма на алгоритмическом языке нужно соблюдать некоторые правила.

Источник: videouroki.net

§ 12. Алгоритмы и величины

Часто эту последовательность называют технологической цепочкой решения задачи на компьютере. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5.

На этапе постановки задачи должно быть четко определено, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимый для решения задачи.

Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение задачи требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели.

Третий этап — построение алгоритма. Опытные программисты часто сразу пишут программы на языках программирования, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования.

Первые три этапа — это работа без компьютера. Дальше следует собственно программирование на определенном языке в определенной системе программирования. Последний (шестой) этап — это уже использование разработанной программы в практических целях. Выполнение учебных заданий на программирование обычно заканчивается пятым этапом, т. е. доказательством правильности составленной программы.

• уметь строить алгоритмы;
• знать языки программирования;
• уметь работать в соответствующей системе программирования.

Основой программистской грамотности является развитое алгоритмическое мышление.

Понятие алгоритма

Одним из фундаментальных понятий в информатике является понятие алгоритма. Сам термин «алгоритм» пришел из математики. Это слово происходит от «Algorithmi» — латинского написания имени Мухамеда аль-Хорезми (787-850 гг.), выдающегося математика средневекового Востока.

В XII веке был осуществлен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение «столбиком», деление «уголком» многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, вычисление корней уравнений также можно отнести к математическим алгоритмам.

В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем. В школьном курсе информатики с понятием алгоритма, с методами построения алгоритмов ученики впервые знакомятся на примерах учебных исполнителей: Робота, Черепашки, Чертежника и др. В нашем учебнике для 9 класса описан графический исполнитель — ГРИС.

Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке.

В разделе информатики под названием «Программирование» изучаются методы программного управления работой компьютера. Следовательно, в качестве исполнителя выступает компьютер. Он работает с величинами — различными информационными объектами: числами, символами, кодами и пр. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами.

Данные и величины

Совокупность величин, с которыми работает компьютер, принято называть данными. По отношению к программе данные делятся на исходные, результаты, (окончательные данные) и промежуточные данные, которые получаются в процессе вычислений (рис. 3.1).

Рис. 3.1. Уровни данных относительно программы

Например, при решении квадратного уравнения: ах 2 + Ьх + с = 0 исходными данными являются коэффициенты а, b, с; результатами — корни уравнения х1, х2; промежуточными данными — дискриминант уравнения: D = b 2 — 4ас.

Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина занимает свое определенное место в памяти компьютера. Иногда говорят — ячейку памяти. Хотя термин «ячейка», с точки зрения архитектуры современных компьютеров, несколько устарел, однако в учебных целях его удобно использовать.

У всякой величины имеются три основных свойства: имя, значение и тип. На уровне команд процессора величина идентифицируется адресом ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные. Константа — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, ‘к’, true.

Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, cod15. Любая константа или переменная занимают ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке.

Теперь о типах величин — типах данных. С понятием типа данных вы уже встречались, изучая в курсе информатики основной школы электронные таблицы и базы данных. Это понятие является фундаментальным для программирования.

В каждом языке программирования существует своя концепция типов данных, своя система типов. Однако в любой язык входит минимально необходимый набор основных типов данных, к которому относятся целый, вещественный, логический и символьный типы. С типом величины связаны три ее свойства: множество допустимых значений, множество допустимых операций, форма внутреннего представления. В таблице 3.1 представлены эти свойства основных типов данных.

Таблица 3.1

Типы констант определяются по контексту (т. е. по форме записи в тексте), а типы переменных устанавливаются в описаниях переменных.

Есть еще один вариант классификации данных: классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина — одно значение. Для структурированных: одна величина — множество значений.

К структурированным величинам относятся массивы, строки, множества и др.

Компьютер — исполнитель алгоритмов. Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя, в рамках его системы команд. О каком же исполнителе идет речь в теме «Программирование обработки информации»? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс: компьютер + система программирования (СП).

Программист составляет программу на том языке, на который ориентирована СП. Схематически это изображено на рис. 3.2, где входным языком исполнителя является язык программирования Паскаль.

Рис. 3.2. Взаимодействие программиста с компьютером

• присваивания;
• ввода;
• вывода;
• обращения к вспомогательному алгоритму (подпрограмме);
• цикла;
• ветвления.

Для описания алгоритмов в дальнейшем мы будем использовать блок-схемы и учебный Алгоритмический язык, применяемый в школьном курсе информатики.

Система основных понятий

Вопросы и задания

1. Перечислите и охарактеризуйте этапы решения задач на компьютере.
2. Дайте определение алгоритма.
3. Что такое «система команд исполнителя алгоритмов» (СКИ)?
4. Какими возможностями обладает компьютер как исполнитель алгоритмов?
5. Назовите команды, входящие в СКИ компьютера, из которых составляется любая программа обработки данных.
6. Перечислите различные варианты классификации данных.
7. Придумайте пример задачи, решаемой на компьютере, и назовите для нее исходные, промежуточные и итоговые данные.

Источник: tepka.ru