Соберите программу нахождения площади треугольника если даны длины его сторон program geom 1

Содержание

Треугольник — не самая популярная фигура в природе и в нашей обычной жизни. Но ей постоянно пользуются дизайнеры одежды, ювелиры, архитекторы. И, наверняка, нахождение площади треугольника является их частой задачей. Подробнее на эту тему поговорим в статье.

· Обновлено 2 марта 2023

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Популярные единицы измерения площади:

  • квадратный миллиметр (мм 2 );
  • квадратный сантиметр (см 2 );
  • квадратный дециметр (дм 2 );
  • квадратный метр (м 2 );
  • квадратный километр (км 2 );
  • гектар (га).

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Нахождение площади треугольника в С++

Источник: skysmart.ru

Площадь треугольника по координатам вершин

Как найти площадь треугольника по координатам его вершин?

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

вывести формулу для нахождения площади и использовать её для вычисления.

Площадь треугольника ABC с вершинами в точках A(x1;y1), B(x2;y2), C(x3;y3) можно вычислить с помощью формулы

[S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|.]

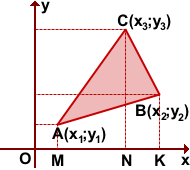
ploshchad-treugolnika-po-koordinatam

Рассмотрим треугольник ABC,

Опустим перпендикуляры из вершин треугольника на координатные оси.

[S_{Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK} ]

[S_{MACN} = frac{{MA + CN}}{2} cdot MN = frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ),]

[S_{NCBK} = frac{{NC + BK}}{2} cdot NK = frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ),]

[S_{MABK} = frac{{MA + BK}}{2} cdot MK = frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ).]

Вычисление площади треугольника через основание и высоту в программе на языке Паскаль

[= frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ) + frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ) - frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ) = ]

[= frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] = ]

[= frac{1}{2}[x_3 y_1 - x_1 y_1 underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 - ]

[- x_2 y_1 + x_1 y_1 - x_2 y_2 + x_1 y_2 ] =]

[= frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) + ]

[+ ( - x_3 y_2 + x_3 y_1 )] = ]

[= frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] = ]

[= frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].]

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

[ S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|. ]

Что и требовалось доказать.

Читайте также:
Как называется программа для работы с устройствами компьютера

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

Находим длины сторон треугольника ABC.

[AB = sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 } ]

[ AB = sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = sqrt {16 + 49} = sqrt {65} ;]

[AC = sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 } ]

[AC = sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = sqrt {36 + 4} = sqrt {40} ;]

[BC = sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 } ]

[BC = sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = sqrt {4 + 81} = sqrt {85} .]

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

[S_{Delta ABC} = frac{1}{2}left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} right| = ]

[= frac{1}{2}left| {4 cdot ( - 2) - 6 cdot 7} right| = frac{1}{2} cdot 50 = 25.]

Угол A образован векторами AC и AB. Отсюда

[ cos angle A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{left } right| cdot left| {overrightarrow {AC} } right|}} ]

Находим координаты векторов:

[overrightarrow {AB} (x_B - x_A ;y_B - y_A )]

[overrightarrow {AB} (3 - ( - 1);4 - ( - 3))]

[overrightarrow {AC} (x_C - x_A ;y_C - y_A )]

[overrightarrow {AC} (5 - ( - 1); - 5 - ( - 3))]

[overrightarrow {AB} cdot overrightarrow {AC} = 4 cdot 6 + 7 cdot ( - 2) = 10.]

Длины AB и AC уже знаем:

[left| {overrightarrow {AB} } right| = sqrt {65} ,left| {overrightarrow {AC} } right| = sqrt {40} .]

[cos angle A = frac{{10}}{{sqrt {65} cdot sqrt {40} }} = frac{{10}}{{sqrt {5 cdot 13} cdot sqrt {5 cdot 4 cdot 2} }} = ]

Синус и косинус одного угла связаны соотношением:

[sin ^2 angle A + cos ^2 angle A = 1]

Синус угла от 0° до 180° является положительным числом, поэтому

[sin angle A = sqrt {1 - cos ^2 angle A} ]

[sin angle A = sqrt {1 - frac{1}{{26}}} = sqrt {frac{{25}}{{26}}} = frac{5}{{sqrt {26} }}.]

[S_{Delta ABC} = frac{1}{2} cdot AB cdot AC cdot sin angle A,]

[S_{Delta ABC} = frac{1}{2} cdot sqrt {65} cdot sqrt {40} cdot frac{5}{{sqrt {26} }} = 25.]

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

[left{ begin{array}{l} - 3 = k cdot ( - 1) + b \ 4 = k cdot 3 + b \ end{array} right.]

[y = frac{7}{4}x - frac{5}{4},4y = 7x - 5,]

[d = frac{left right|}}{{sqrt {7^2 + 4^4 } }} = frac{{50}}{{sqrt {65} }}.]

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

Источник: www.treugolniki.ru

Расчет площади треугольника

В то далёкое время, когда Паша ходил в школу, ему очень не нравилась формула Герона для вычисления площади треугольника, так как казалась слишком сложной. В один прекрасный момент Павел решил избавить всех школьников от страданий и написать и распространить по школам программу, вычисляющую площадь треугольника по трём сторонам.

Одна проблема: так как эта формула не нравилась Павлу, он её не запомнил. Помогите ему завершить доброе дело и напишите программу, вычисляющую площадь треугольника по переданным длинам трёх его сторон по формуле Герона.

На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.

a = int(input()) # ввод трех сторон треугольника b = int(input()) c = int(input()) p = (a + b + c) / 2 #расчет полупериметра для формулы Герона s = (p * (p — a) * (p — b) * (p — c))**0.5 #расчет площади по формуле Герона print (s)

Читайте также:
Какое действие нужно сделать чтобы повысить скорость визуализации в программе autodesk 3ds max

Похожие записи:

  1. Эффективный ввод-вывод в разных языках программирования
  2. Django — доработка шаблона формы регистрации
  3. Периметр треугольника
  4. Расчет площади фигур

Источник: mob25.com

Рейтинг
( Пока оценок нет )
Комментарии0
Загрузка ...
Похожие материалы
EFT-Soft.ru