Структурное программирование — это подход к разработке программного кода, который включает в себя разделение программы на подзадачи с использованием последовательных, условных и циклических операторов. Преимущества этой технологии заключаются в повышении понимаемости кода, улучшении его структурированности, уменьшении ошибок и упрощении тестирования.
2. Какой алгоритм называется вспомогательным?
Вспомогательный алгоритм — это алгоритм, который используется в других алгоритмах или процедурах для выполнения определенных задач. Он может быть вынесен в отдельную функцию или процедуру, чтобы облегчить повторное использование кода.
3. Вспомните, в чём состоит суть метода последовательного построения (уточнения) алгоритма. Как он называется иначе?
Метод последовательного построения (уточнения) алгоритма — это подход, при котором алгоритм разрабатывается постепенно, с постоянным уточнением деталей и улучшением его работоспособности. Этот метод также называют методом итераций.
Установка необходимых программ для Windows (Installpack)
4. Опишите основные шаги разработки программы методом «сверху вниз».
Шаги разработки программы методом «сверху вниз» включают:
• Определение задачи, которую должна решать программа
• Разбиение задачи на подзадачи более низкого уровня
• Разработка алгоритмов для каждой из подзадач
• Объединение подзадач в общий алгоритм
• Написание кода для каждого из шагов алгоритма
• Тестирование и отладка программы
5. Дан прямоугольный параллелепипед, длины рёбер которого равны а, b и с.
Требуется определить периметр треугольника, образованного диагоналями его граней. Какой алгоритм целесообразно использовать при решении этой задачи в качестве вспомогательного?
6. Какой вспомогательный алгоритм называется рекурсивным? Что такое граничное условие и каково его назначение в рекурсивном алгоритме?
7. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
Требуется выяснить, чему равно значение функции F(10).
8. Исполнитель Калькулятор имеет следующую систему команд:
1) прибавь 1;
2) умножь на 2.
С помощью первой из них исполнитель увеличивает число на экране на 2, с помощью второй — в 2 раза.
1) Выясните, сколько разных программ, преобразующих число 1 в число 20, можно составить для этого исполнителя.
2) Сколько среди них таких программ, у которых в качестве промежуточного результата обязательно получается число 15?
3) Сколько среди них таких программ, у которых в качестве промежуточного результата никогда не получается число 12?
9. Попробуйте найти рекурсивные синтаксические структуры:
1) в поэме А. Блока «Двенадцать»;
2) в стихотворении М. Лермонтова «Сон»;
3) в романе М. Булгакова «Мастер и Маргарита»;
4) в фольклоре.
10. Найдите информацию о таких геометрических фракталах, как Снежинка Коха, Т-квадрат, Н-фрактал, кривая Леви, Драконова ломаная.
InstallPack — необходимые программы всегда под рукой
11. Напишите программу вычисления значения функции F(n), рассмотренной в примере 4 этого параграфа. Вычислите с её помощью значение функции F(7).
12. Напишите программу вычисления
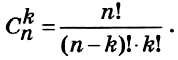
Используйте подпрограмму.
13. Дана программа:
Не выполняя программу на компьютере, выясните, что получится в результате работы этой программы.
Проверьте свой результат, выполнив программу на компьютере.
Источник: izi-otvet.ru
Учитель информатики

Компьютер может исполнять алгоритм, если алгоритм написан на одном из языков программирования. Алгоритм, написанный на одном из языков программирования, называют программой.
Программу нужно ввести в память компьютера и запустить на исполнение. Тогда программа автоматически выполняется компьютером. Поэтому говорят, что компьютер — исполнитель алгоритмов.
Объект можно назвать исполнителем алгоритма, если он обладает следующими свойствами:
Исполнитель-компьютер ничего не знает и не понимает. Он формально выполняет программу, то есть последовательность команд, которые входят в систему его команд и написаны для него на специальном языке программирования.
Компьютер никогда не задает вопросов «Почему?» и «Зачем?». Он не отказывается выполнять команды, которые входят в его систему команд. Поэтому компьютер называют формальным исполнителем алгоритмов.
Человек тоже может быть формальным исполнителем. Как правило, человек понимает, что он делает и зачем, поэтому он может отказаться от выполнения команд, которые умеет выполнять, но не считает возможным.
Человек может не выполнить какое-либо действие по моральным соображениям или соблюдая свою безопасность. Например, человек может отказаться обижать маленьких или слабых, прыгать с опасной для жизни высоты и так далее. То есть он может это сделать, но не хочет.
Как мы уже говорили, компьютер называют универсальным исполнителем, так как он может обрабатывать данные разных видов: звуковые, текстовые, числовые, графические.
Универсальным исполнителем компьютер можно назвать ещё и потому, что его могут использовать разные люди: математики, писатели, медики, инженеры, учителя, студенты, школьники и даже маленькие дети. Всё это возможно, так как в памяти компьютера много разных программ.

Одни программы управляют самим компьютером. Это системные программы. Другие программы помогают создавать и редактировать информационные объекты (тексты, рисунки, схемы, числа и другое). Такие программы называются прикладными. Есть и другие виды программ.
2.1.1. Понятие алгоритма
Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.
Пример 1. Задача «Найти среднее арифметическое двух чисел» решается в три шага:
- 1) задумать два числа;
- 2) сложить два задуманных числа;
- 3) полученную сумму разделить на 2.
Пример 2. Задача «Внести деньги на счёт телефона» подразделяется на следующие шаги:
- 1) подойти к терминалу по оплате платежей;
- 2) выбрать оператора связи;
- 3) ввести номер телефона;
- 4) проверить правильность введённого номера;
- 5) вставить денежную купюру в купюроприёмник;
- 6) дождаться сообщения о зачислении денег на счёт;
- 7) получить чек.
Пример 3. Этапы решения задачи «Нарисовать весёлого ёжика» представлены графически:

Нахождение среднего арифметического, внесение денег на телефонный счёт и рисование ежа — на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.
Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (примеры 2-3). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.
В общем виде схему работы алгоритма можно представить следующим образом (рис. 2.1).

Алгоритмами являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.
Анимации «Работа с алгоритмом» (193576), «Наибольший общий делитель» (170363), «Наименьшее общее кратное» (170390) помогут вам вспомнить некоторые алгоритмы, изученные на уроках русского языка и математики (http://sc.edu.ru/).
Пример 4. Некоторый алгоритм приводит к тому, что из одной цепочки символов получается новая цепочка следующим образом:
- 1. Вычисляется длина (в символах) исходной цепочки символов.
- 2. Если длина исходной цепочки нечётна, то к исходной цепочке справа приписывается цифра 1, иначе цепочка не изменяется.
- 3. Символы попарно меняются местами (первый — со вторым, третий — с четвёртым, пятый — с шестым и т. д).
- 4. Справа к полученной цепочке приписывается цифра 2.
Получившаяся таким образом цепочка является результатом работы алгоритма.
3. Алгоритмическая конструкция следование
Существует большое количество алгоритмов, в которых все команды выполняются последовательно одна за другой в том порядке, в котором они записаны. В подобных алгоритмах отсутствуют команды, меняющие порядок выполнения других команд. Такие программы вы составляли в прошлом году для исполнителя Чертежник.
Алгоритмическая конструкция следование — последовательность команд алгоритма, которые выполняются в том порядке, в котором они записаны.
Следование использовалось в примере 8.3, в котором описывались алгоритмы вычисления длины и ширины участка и построения прямоугольника исполнителем Чертежник.
Алгоритмическая конструкция следование представлена в примере 8.4 и примере 8.5.
25 баллов?
Вводится последовательность вещественных чисел.
Признак конца ввода – 0.
Определить является ли последовательность упорядоченной по убыванию.

Программист написал программу на языке машинных команд, которая последовательнно размещается в памяти начиная с нулевого адреса.
Каждая команда занимает 4 байта памяти.
16ричный адрес последней команды в программе равен 28.
Сколько команд содержит эта программа?

Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока.
Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:

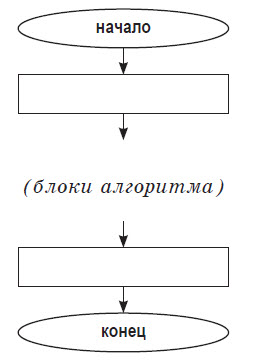
Общий вид блок–схемы алгоритма:
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
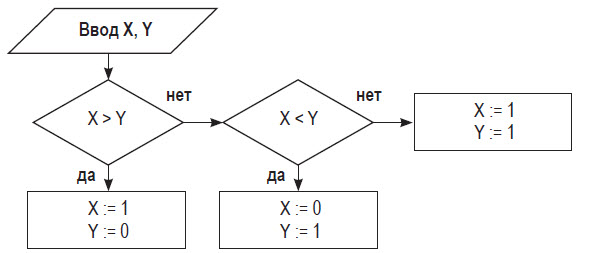
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7
Источник: fobosworld.ru
Этапы решение задачи на компьютере. Принцип последовательного конструирования алгоритма

В этом видеоуроке рассматриваются этапы решения задачи на компьютере и их особенности. Наиболее подробно рассматривается этап создания алгоритма. Ученики узнают, что при необходимости разработки сложного алгоритма можно использовать принцип последовательного конструирования алгоритма. Будет также рассмотрен принцип его работы.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока «Этапы решение задачи на компьютере. Принцип последовательного конструирования алгоритма»
· Этапы решения задачи на компьютере.
· Принцип последовательного конструирования алгоритма.
Давайте подумаем, с чего начинается решение любой задачи, не обязательно связанной с компьютером. Решение любой задачи начинается с прочтения и уточнения её условия. Условия задач мы рассматривали в текстовой форме. Мы выделяли информацию, которая дана в условии – входные данные, а также информацию которую необходимо получить – выходные данные. Это начальный этап решения задачи, то есть её постановка.
После того, как мы определили входные и выходные данные задачи, нам нужно определиться со средствами, которые могут быть необходимы для получения выходных данных из входных. Для этого определяются отношения между ними и записываются на каком-нибудь формальном языке, например, с помощью математических формул. Результатом этих действий будет информационная модель задачи, записанная на некотором формальном языке. Этот этап называется формализацией задачи.
После того, как мы определились со средствами решения задачи, нужно понять, что необходимо сделать для того, чтобы получить выходные данные из входных, какие действия над информацией и в каком порядке для этого нужно произвести. То есть мы составляем алгоритм решения задачи и описываем его одним из известных нам способов, например, с помощью блок-схемы или в текстовой форме. Главное, чтобы было понятно, что должна делать программа и в каком порядке. Этот этап называется созданием алгоритма.
Далее мы записывали созданный алгоритм с помощью языка программирования или других инструментов. И получали компьютерную программу для решения задачи. Этот этап имеет простое название: программирование.
Получив компьютерную программу, мы обычно проверяли правильность её работы. Сначала пробовали запустить программу. После чего задавали несколько различных вариантов входных данных, для которых выходные данные уже были известны, и проверяли, совпадают ли они с теми, которые возвращает программа. Если данные совпадают – программа работает правильно и задача решена.
Если же не совпадают – на каком-то из этапов была допущена ошибка. Этот процесс называется тестированием программы.
Ошибки в программе бывают двух видов: синтаксические и логические. Синтаксические ошибки связаны с записью программы на конкретном языке программирования и, как правило, находятся и исправляются средствами среды разработки. Логические ошибки обычно допускаются на более ранних этапах.
После того, как ошибка была исправлена, снова проделываются все этапы, следующие за тем, на котором допущена ошибка. Так происходит до тех пор, пока правильность работы программы не подтверждается. Этот процесс называется отладкой.
Таким образом, мы выделили пять этапов решения задачи с помощью компьютера: постановка задачи, формализация задачи, создание алгоритма, программирование, тестирование и отладка. Все эти этапы мы выполняли при решении задач и раньше, но для экономии времени часто этапы формализации задачи и создания алгоритма мы объединяли между собой.
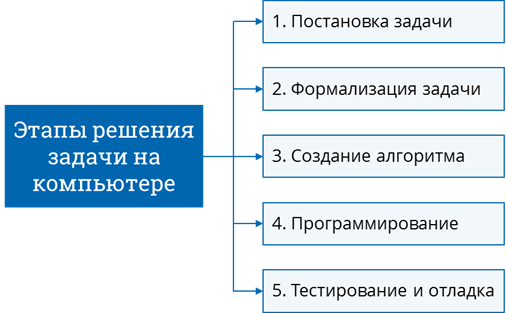
Но предположим, что у нас есть задача, для которой мы уже описали формальную информационную модель, однако придумать алгоритм для решения задачи у нас не выходит, потому что он получается слишком большим и сложным. Чтобы облегчить эту задачу, можно использовать принцип последовательного конструирования алгоритма, этот принцип также называется «разработкой сверху вниз» или методом «пошаговой детализации».
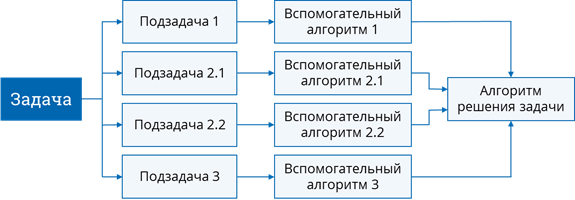
Он состоит в том, что задача разбивается на несколько более простые подзадач, каждая из которых также может разбиваться на подзадачи. Так происходит до тех пор, пока не станет понятным, как решать каждую отдельную подзадачу. Для решения каждой задачи составляется вспомогательный алгоритм. После того, как мы составили вспомогательные алгоритмы для решения всех подзадач, нам остаётся лишь собрать их воедино. Таким образом, мы получим алгоритм для решения исходной задачи.
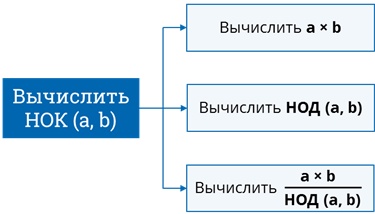
Рассмотрим задачу. Написать программу, вычисляющую наименьшее общее кратное двух целых положительных чисел a и b. Наименьшим общим кратным (НОК) двух натуральных чисел называется наименьшее целое число, которое без остатка делится на оба числа. Из курса математики нам известно, что наименьшее общее кратное двух натуральных чисел можно вычислить как их произведение, делённое на их наибольший общий делитель (НОД). Таким образом, исходную задачу мы можем разбить на 3 подзадачи: вычислить произведение введённых чисел, вычислить их наибольший общий делитель и разделить произведение чисел на их наибольший общий делитель.
Решение первой и третьей подзадач очевидно. Также ранее мы узнали, что наибольший общий делитель двух чисел можно найти, использовав усовершенствованный алгоритм Эвклида, который состоит в том, чтобы заменять большее число в паре его остатком от деления на другое до тех пор, пока одно из чисел не станет равным нулю. После этого ненулевое число будет равным наибольшему общему делителю исходных чисел.
Начнём написание программы для решения задачи. Вначале с помощью инструкции print выведем на экран сообщение о том, что это программа, вычисляющая наименьшее общее кратное целых положительных чисел a и b. С помощью следующей инструкции print выведем на экран запрос на ввод a без перехода на следующую строку. Далее запишем инструкцию для считывания a.
Так как по условию задачи a и b – это целые числа, при считывании будем преобразовывать их значения в целочисленный тип int. Теперь скопируем последние две инструкции и изменим их для считывания значения Бэ.
Далее вычислим произведение a и b в переменной p. Таким образом, первая подзадача будет решена. Далее вычислим наибольший общий делитель a и b. Для этого запишем цикл while, который будет повторяться, пока a ≠ 0 и b ≠ 0. Тело цикла будет содержать ветвление, определяющее, какое из чисел наибольшее. Его условием будет: a > b.
Если это условие выполняется, то число a на этом шаге цикла наибольшее и согласно алгоритму Эвклида, мы заменим его остатком от деления a на b. Если же условие ветвления не выполняется, то наибольшим числом на этом шаге цикла является b, и мы заменим его остатком от деления b на a. Когда одно из чисел a или b станет равным 0, цикл завершит свою работу и мы вычислим наибольший общий делитель исходных чисел в переменной nod как сумму текущих значений a и b. Таким образом мы решили вторую подзадачу.
Теперь, чтобы вычислить наименьшее общее кратное введённых чисел, присвоим переменной nok значение переменной p, делённое на значение переменной nod. Так как наименьшее общее кратное – целое число, используем для этого операцию целочисленного деления. Таким образом мы решили третью подзадачу. С помощью инструкции print выведем на экран поясняющее сообщение о том, что наибольшее общее кратное a и b равно значению переменной nok.
print (‘Программа, вычисляющая НОК a и b.’)
while a != 0 and b != 0:
print (‘НОК введённых чисел:’, nok)
Сохраним написанную программу и протестируем её. Запустим программу на выполнение и зададим числа 2 и 3. Действительно, наименьшее число, которое без остатка делится и на 2, и на 3 – 6. Снова запустим программу и зададим числа 6 и 8. Действительно, наименьшее число, которое без остатка делится и на 6, и на 8 – 24. Программа работает правильно. Задача решена.
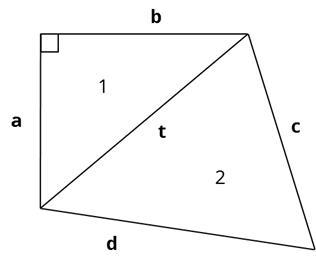
Рассмотрим ещё одну задачу. Выпуклый четырёхугольник задан положительными длинами своих сторон: a, b, c и d. Написать программу для вычисления его площади, если известно, что между сторонами a и b прямой угол.
Изобразим условие этой задачи в виде рисунка. Соединим противоположные концы сторон a и b отрезком, длину которого обозначим t. Таким образом мы разделили четырёхугольник на два треугольника со сторонами a, b, t и c, d, t соответственно. Площадь четырёхугольника равна сумме их площадей.
Так как между сторонами a и b прямой угол, то площадь первого треугольника можно вычислить как полупроизведение a и b, а t – как гипотенузу первого треугольника. Зная значения c, d и t, мы можем вычислить площадь второго треугольника по формуле Герона. Таким образом, мы записали формулы, необходимые для решения задачи, получив математическую модель.
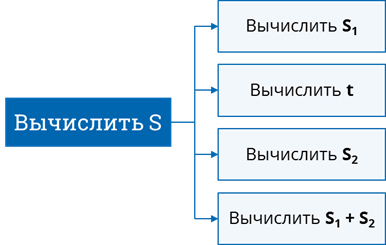
Также мы разобьём задачу на несколько подзадач. Вначале мы вычислим площадь первого треугольника, после чего определим длину стороны t. Далее мы вычислим площадь второго треугольника и в конце рассчитаем площадь четырёхугольника как сумму площадей треугольников, из которых он состоит. Так мы составили алгоритм решения задачи.
Начнём написание программы. Вначале с помощью инструкции print выведем на экран сообщение о том, что это программа, вычисляющая площадь четырёхугольника по длинам его сторон. Угол между сторонами a и b прямой. С помощью следующей инструкции print выведем на экран запрос на ввод a без перехода на следующую строку. Запишем инструкции для считывания значения a.
Так как в условии задачи не сказано, что длины сторон – целые числа, при считывании мы будем преобразовывать их значения в вещественный тип float. Скопируем последние две инструкции три раза и изменим их для считывания значений переменных b, c и d. После того как мы рассчитали длины сторон четырёхугольника, вычислим площадь первого треугольника в переменной s1.
Для этого присвоим ей значение a * b / 2. Так как для вычисления длины гипотенузы треугольника нам потребуется извлечь квадратный корень, загрузим эту функцию из модуля math в описываемый модуль. После этого вычислим длину гипотенузы первого треугольника в переменной t. Для этого присвоим ей значение квадратного корня из суммы квадратов a и b.
Теперь вычислим полупериметр второго треугольника в переменной p. Для этого присвоим ей значение полусуммы c, d и t. Далее вычислим по формуле Герона площадь второго треугольника в переменной s2. Для этого присвоим ей значение квадратного корня из произведения p * (p – c) * (p – d) * (p – t).
И, наконец, вычислим площадь четырёхугольника в переменной s, присвоив ей значение суммы s1 и s2. С помощью инструкции print выведем на экран сообщение о том, что площадь четырёхугольника равна значению переменной s. Будем выводить s с точностью в четыре знака после запятой.
print (‘Программа, вычисляющая площадь четырёхугольника по длинам его сторон. Угол между a и b прямой.’)
from math import sqrt
t = sqrt (a ** 2 + b ** 2)
s2 = sqrt (p * (p — c) * (p — d) * (p — t))
print (‘Площадь заданного четырёхугольника:’, ».format (s))
Сохраним описанный модуль и протестируем его. Сначала в качестве четырёхугольника зададим квадрат со стороной, равной 5. Его площадь действительно равна 25. Снова запустим программу на выполнение и зададим четырёхугольник с длинами сторон: 3, 4, 12 и 13. Очевидно, что площадь первого треугольника равна 6, а его гипотенуза – 5. По формуле Герона площадь второго треугольника равна 30.
Значит площадь четырёхугольника равна 36. Программа вывела сообщение об этом, это значит, что она работает верно и задача решена.
· Решение любой задачи с помощью компьютера состоит из пяти этапов: постановка задачи, её формализация, создание алгоритма, программирование, тестирование и отладка.
· Если алгоритм решения задачи сложно придумать сразу, то для этого можно использовать метод последовательного конструирования алгоритма, где задача разбивается на несколько более простых подзадач, каждая из которых также может делиться на подзадачи. Так происходит до тех пор, пока нам не станет понятно, каким образом решить все подзадачи. После этого решения всех подзадач соединяются воедино, образуя алгоритм решения исходной задачи.
Источник: videouroki.net