Чтобы купить курс,
пожалуйста, войдите
или зарегистрируйтесь
Вход/Регистрация Быстрый заказ
Быстрая регистрация
Информатика (Вариант 2)
Купить видеоуроки |
Приобретите наш курс
Для продолжения просмотра купите полный курс
наших видеоуроков
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
| вверх | вниз | влево | вправо |
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ (также по отношению к наблюдателю):
| сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Робот ЕГЭ Информатика
выполняется, пока условие истинно.
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции. Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
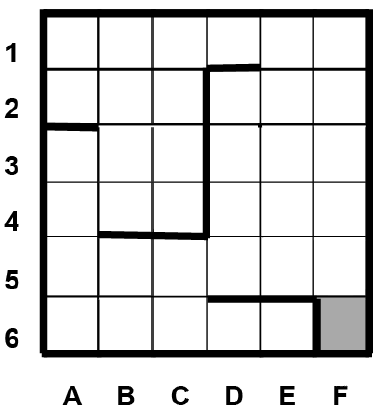
ПОКА снизу свободно ИЛИ справа свободно
ЕСЛИ снизу свободно
ТО вниз
ИНАЧЕ вправо
Источник: 5splusom-school.ru
Тест по информатике Алгоритмические структуры 11 класс
Тест по информатике Алгоритмические структуры 11 класс с ответами. Тест включает 5 заданий с выбором ответа.
1. Какое определение можно использовать для циклического алгоритма?
1) способ представления алгоритма с помощью геометрических фигур
2) алгоритм, содержащий многократные повторения некоторых операторов
3) алгоритм, содержащий условия
4) представление алгоритма в форме таблиц и расчетных формул
2. Какой тип алгоритма должен быть выбран при решении квадратного уравнения?
1) линейный
2) разветвляющийся
3) циклический
4) любой
3. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед n, где n – целое число, вызывающая передвижение черепашки на n шагов в направлении движения.
Разбор 12 задания ЕГЭ по информатике (Поляков в. 52): РОБОТ: Сколько клеток лабиринта
Направо m, где m – целое число, вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Вперед 10 Направо 72]
Какая фигура появится на экране?
1) незамкнутая ломаная линия
2) правильный треугольник
3) квадрат
4) правильный пятиугольник
4. Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив следующую программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка A1)?
НАЧАЛО
ПОКА
ЕСЛИ
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

1) 14
2) 20
3) 26
4) 28
5. Определите значение переменной s после выполнения фрагмента алгоритма.

Ответы на тест по информатике Алгоритмические структуры 11 класс
1. 2
2. 2
3. 4
4. 2
5. 270
Источник: testschool.ru
Презентация Методика решения заданий типа «Робот в лабиринте»










Вы можете ознакомиться и скачать презентацию на тему Методика решения заданий типа «Робот в лабиринте». Доклад-сообщение содержит 23 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.
Слайды и текст этой презентации
Слайд 1

Описание слайда:
Методика решения заданий типа «Робот в лабиринте» Жукова Т.В. МБОУ Заречнская СОШ
Слайд 2

Описание слайда:
Методика решения заданий типа «Робот в лабиринте»
Слайд 3

Описание слайда:
Задания этого типа сводятся к тому, чтобы определить те точки (назовем их «особые») в лабиринте, к которым робот вернется пройдя четыре раза по прямой (пока выполняется условие цикла). При этом он, естественно, пройдет по сторонам прямоугольника.
Задания этого типа сводятся к тому, чтобы определить те точки (назовем их «особые») в лабиринте, к которым робот вернется пройдя четыре раза по прямой (пока выполняется условие цикла). При этом он, естественно, пройдет по сторонам прямоугольника. Очевидно, что «особая» точка – это и стартовая, и финишная позиция. А раз она финишная, то это та точка, в которой нарушилось условие продолжения последнего цикла. На этой идее основан поиск решения задачи.
Слайд 4

Описание слайда:
Задача: Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно снизу свободно слева свободно справа свободно Цикл ПОКА < условие >команда выполняется, пока условие истинно, иначе происходит переход на следующую строку. Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ остановится в той же клетке, с которой он начал движение?
Слайд 5

Описание слайда:
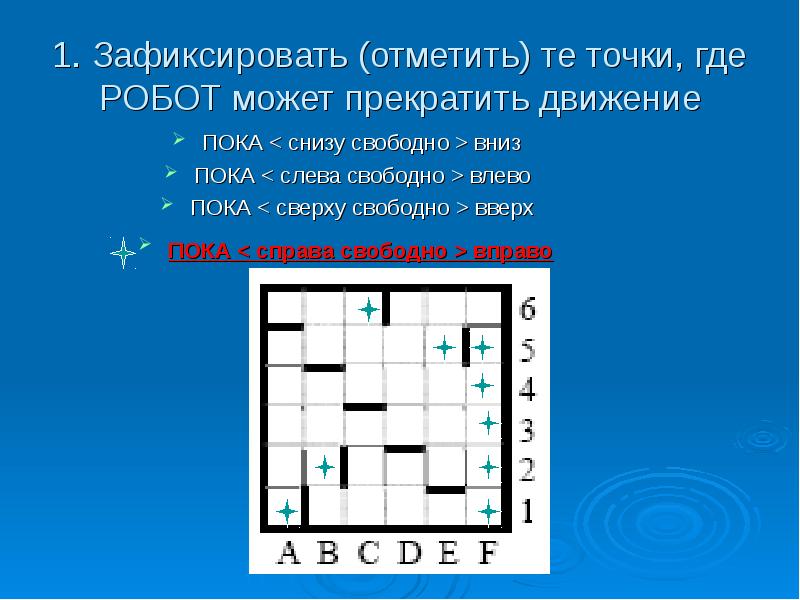
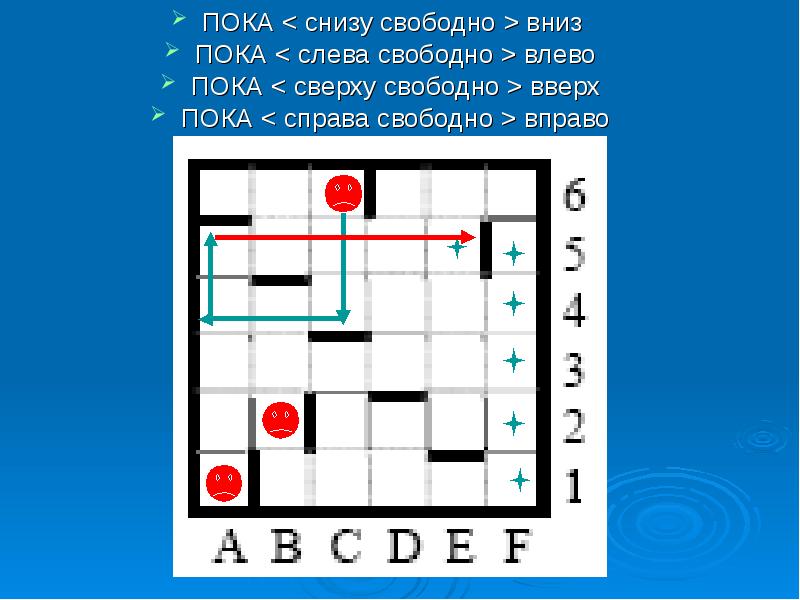
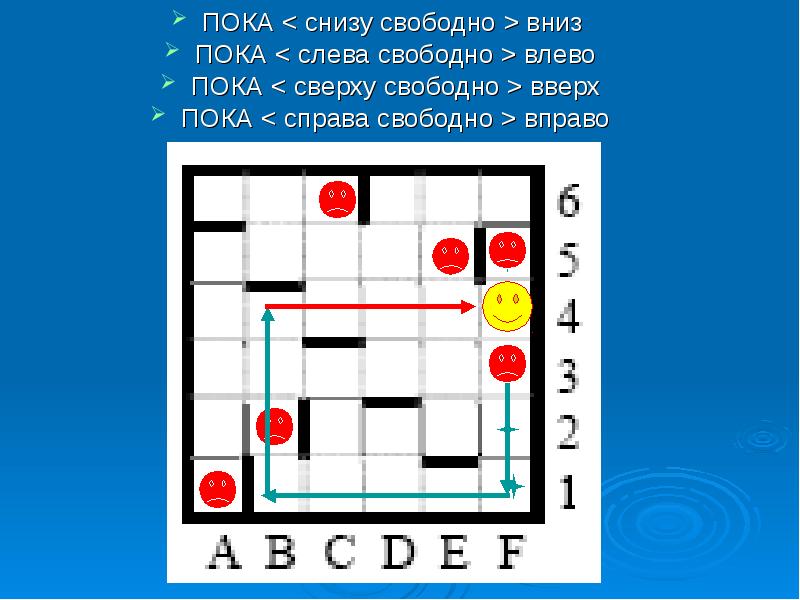
1. Зафиксировать (отметить) те точки, где РОБОТ может прекратить движение ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 6

Описание слайда:
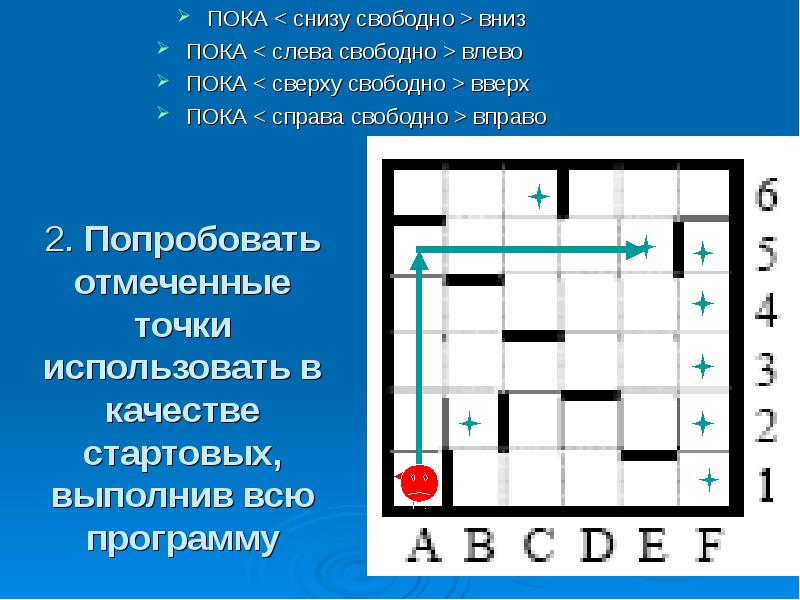
2. Попробовать отмеченные точки использовать в качестве стартовых, выполнив всю программу ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 7

Описание слайда:
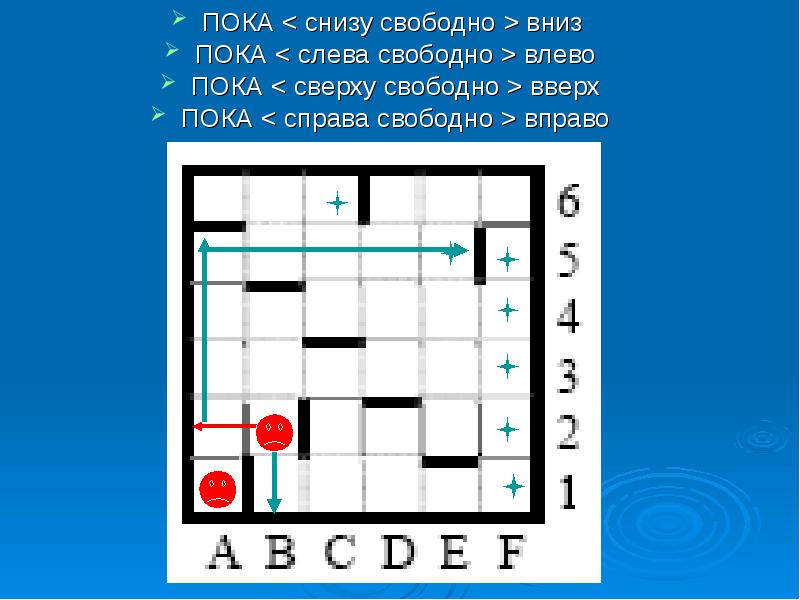
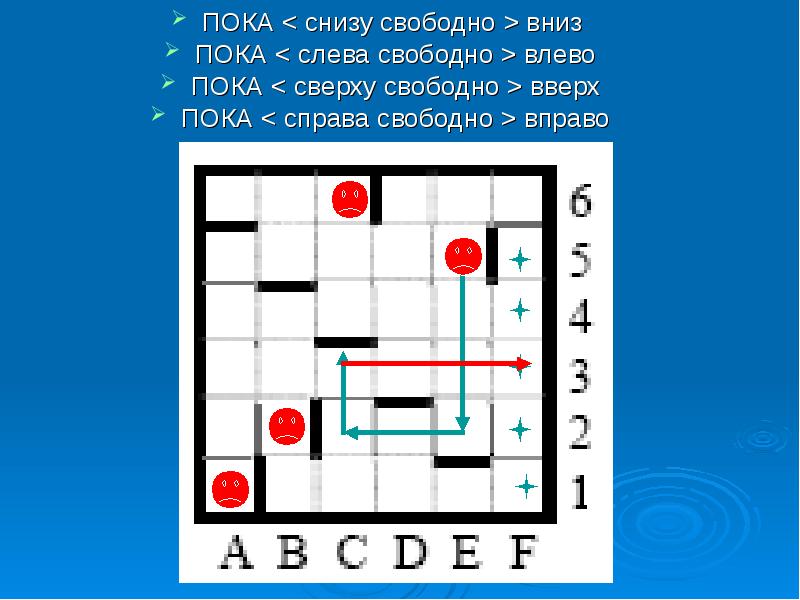
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 8

Описание слайда:
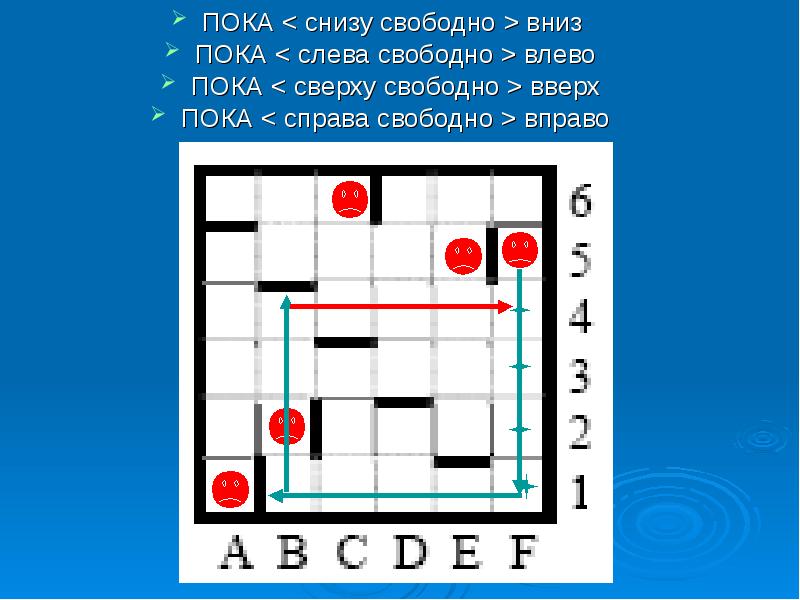
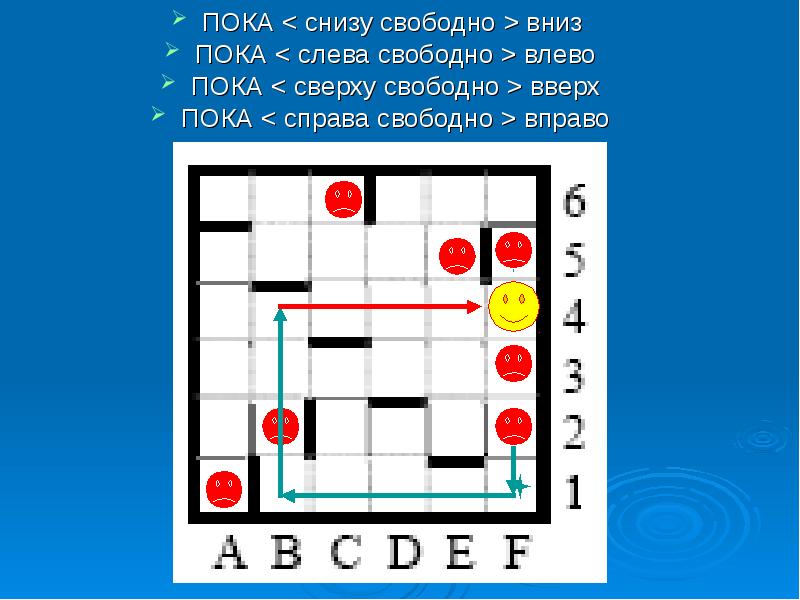
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 9

Описание слайда:
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 10

Описание слайда:
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 11

Описание слайда:
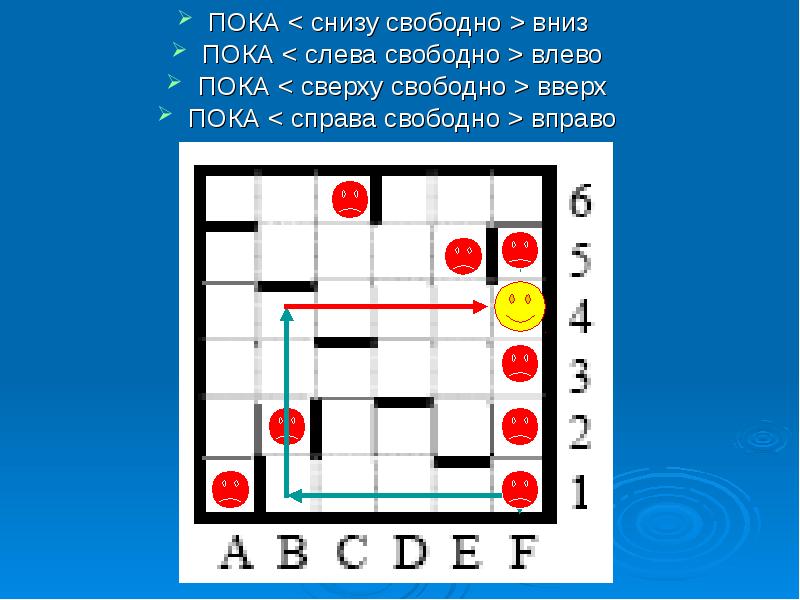
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 12

Описание слайда:
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 13

Описание слайда:
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 14

Описание слайда:
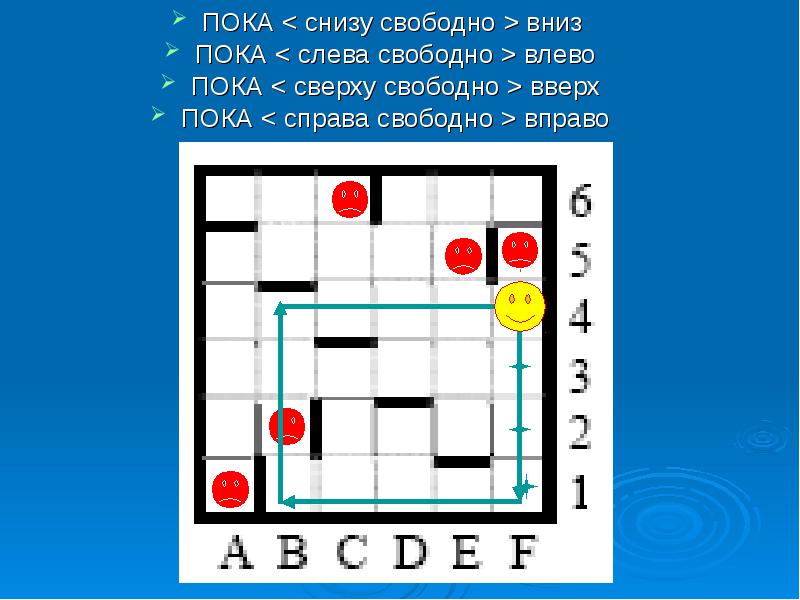
ПОКА < снизу свободно >вниз ПОКА < снизу свободно >вниз ПОКА < слева свободно >влево ПОКА < сверху свободно >вверх ПОКА < справа свободно >вправо
Слайд 15

Описание слайда:
Ответ: Требованию «РОБОТ должен вернуться в исходную точку» удовлетворяет одна клетка. Ответ 1.
Слайд 16

Описание слайда:
Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу, РОБОТ уцелеет (не врежется в стену) и остановится в той же клетке, с которой он начал движение? 1) 1 2) 2 3) 3 4) 0 НАЧАЛО ПОКА <слева свободно>вверх ПОКА вправо ПОКА вниз ПОКА влево КОНЕЦ
Слайд 17

Описание слайда:
Решение: особенность этой задач в том, что РОБОТ проверяет стенку в одном направлении, а движется в другом
Слайд 18

Описание слайда:
рассмотрим первый цикл: рассмотрим первый цикл: ПОКА <слева свободно>вверх понятно, что при движении вверх РОБОТ остановится в первой же клетке, где слева будет стена
Слайд 19

Описание слайда:
рассуждая аналогично, находим, что во втором цикле при движении вправо РОБОТ останавливается в клетке, где есть стена сверху; в третьем цикле (движение вниз) РОБОТ останавливается в клетке, где есть стена справа; рассуждая аналогично, находим, что во втором цикле при движении вправо РОБОТ останавливается в клетке, где есть стена сверху; в третьем цикле (движение вниз) РОБОТ останавливается в клетке, где есть стена справа; наконец, в четвертом цикле РОБОТ останавливается в клетке, где есть стена снизу; при этом он должен попасть обратно в исходную клетку, обозначенную на рисунке красной точкой; кроме этих четырех стенок, необходимо, чтобы коридор, выделенный на рисунке зеленым фоном, был свободен для прохода, иначе РОБОТ врежется в стенку
Слайд 20

Описание слайда:
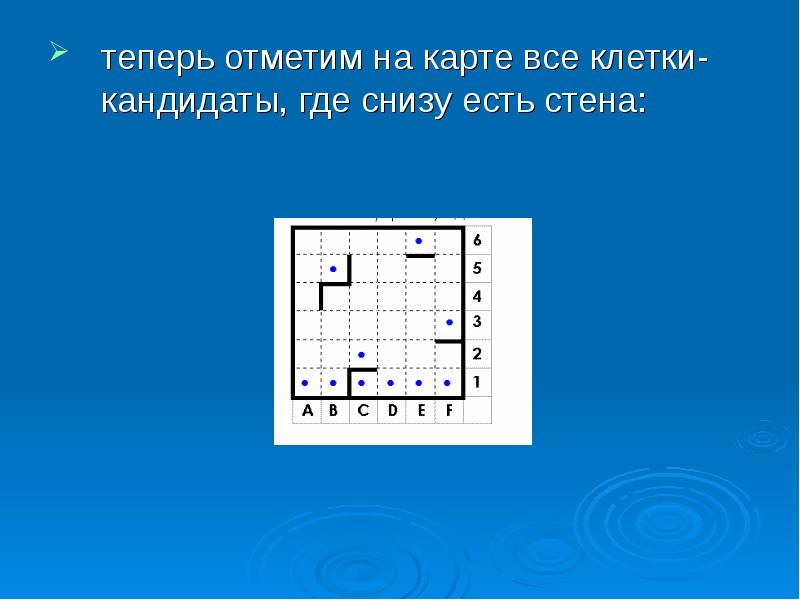
теперь отметим на карте все клетки-кандидаты, где снизу есть стена: теперь отметим на карте все клетки-кандидаты, где снизу есть стена:
Слайд 21

Описание слайда:
при движении из клеток B5, D1, E1, E6, F1 и F3 РОБОТ врежется в стенку, потому что слева стены нет и условие «слева свободно» всегда истинно: при движении из клеток B5, D1, E1, E6, F1 и F3 РОБОТ врежется в стенку, потому что слева стены нет и условие «слева свободно» всегда истинно:
Слайд 22

Описание слайда:
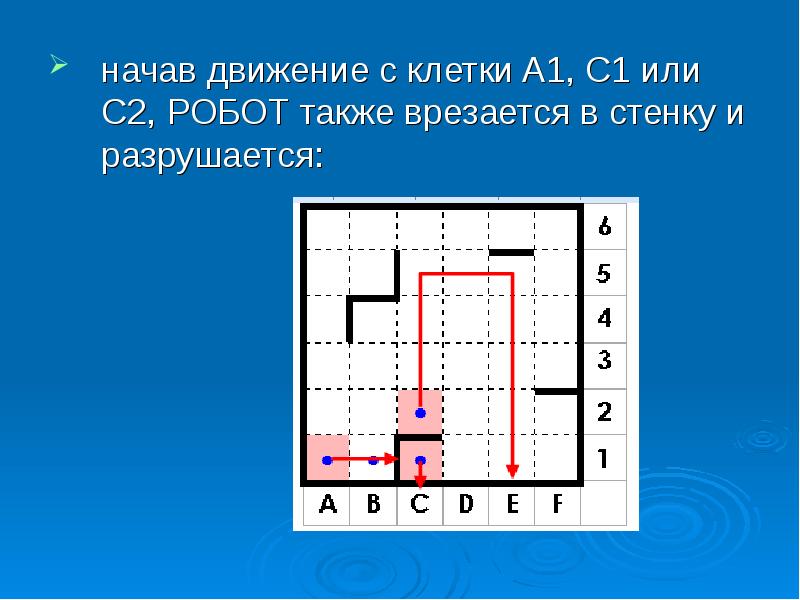
начав движение с клетки A1, C1 или C2, РОБОТ также врезается в стенку и разрушается: начав движение с клетки A1, C1 или C2, РОБОТ также врезается в стенку и разрушается:
Слайд 23

Описание слайда:
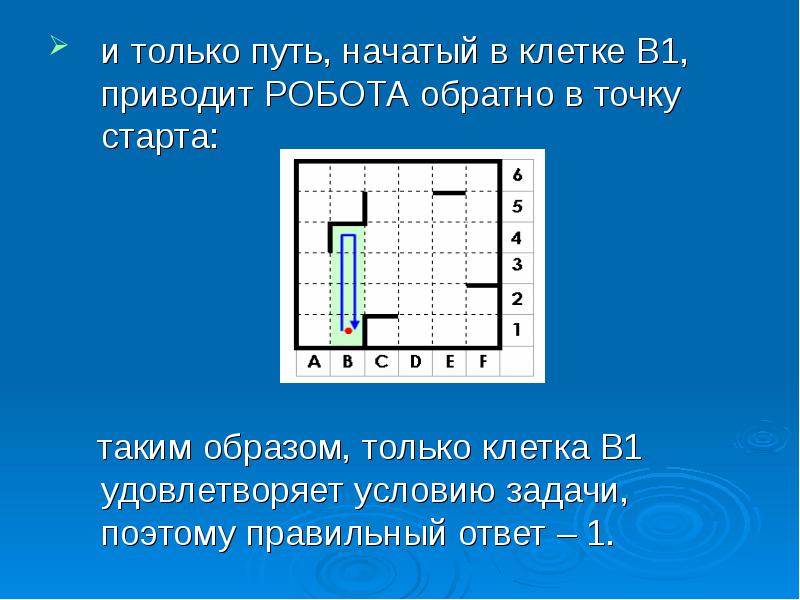
и только путь, начатый в клетке B1, приводит РОБОТА обратно в точку старта: и только путь, начатый в клетке B1, приводит РОБОТА обратно в точку старта: таким образом, только клетка B1 удовлетворяет условию задачи, поэтому правильный ответ – 1.
Источник: mypresentation.ru