Скайлаб что это за программа

Скайлаб что это за программа

Важную роль при обучении решению задач вычислительной математики играет выбор соответствующего программного обеспечения. Сложность и тип решаемых задач во многом зависит от функциональных возможностей выбранной программы. В данной статье в качестве программного обеспечения, используемого на занятиях по вычислительной математике, предлагается программная система Scilab.

Это многофункциональная система, предназначенная для выполнения инженерных и научных вычислений, позволяющая производить сложные алгебраические вычисления, решать задачи дифференцирования и интегрирования, оптимизации и многие другие. Кроме того, следует отметить общедоступность программной системы, что, несомненно, является весомым преимуществом Scilab по сравнению с широко известным пакетом Matlab. Все это способствует успешному применению программной системы Scilab в обучении студентов решению разного рода вычислительных задач. В данной статье приведены примеры некоторых задач вычислительной математики, а также их решение средствами математического пакета Scilab.

Практическая часть лабораторной работы. Компьютерное моделирование в приложении Хсоs, Scilab.

вычислительная математика
математический пакет
линейная алгебра
оптимизация
дифференцирование
интегрирование
дифференциальное уравнение
метод наименьших квадратов

1. Алексеев Е.Р. Scilab: Решение инженерных и математических задач / Е.Р. Алексеев, О.В. Чеснокова, Е.А. Рудченко. – М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008. – 260 с.

2. Бахвалов И.В. Численные методы: учебное пособие / И.В. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – 8-е изд. – М.: Лаборатория Базовых Знаний, 2000. – 624 с.

3. Боден М. Программирование в SciLab / Вики документация SciLab, 2010. URL: http://forge.scilab.org/index.php/p/docprogscilab/downloads/ (дата обращения: 28.06.16).

4. Боев В.Д., Сыпченко Р.П. Компьютерное моделирование. – Москва: ИНТУИТ.РУ, 2010 – 349 с.
5. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002. – 840 с.
6. Королев А.Л.

Компьютерное моделирование. – Москва: БИНОМН, 2010. – 232 с.
7. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1966. – 724 с

Современная вычислительная математика связана с решением разного рода математических задач с применением ЭВМ. Решаемые математические задачи могут быть классифицированы на следующие основные группы:

— алгебраические (решение уравнений (линейных и нелинейных) и их систем, поиск собственных значений, обращение матриц);

— дифференциальные уравнения (задачи дифференцирования и интегрирования функций одной и нескольких переменных, решение обыкновенных дифференциальных уравнений);

— задачи оптимизации (поиск максимального и минимального значений функции на определенном множестве);

— задачи математического программирования – аппроксимации, интерполяции функций и т.д.

Безусловно, возрастающий объем задач требует автоматизации их решения. В этой связи становится весьма актуальным применение для их решения функциональных программных средств. К их числу относятся математические пакеты Matlab, Mathematica, Scilab и др.

Вычисляем значение выражения в Scilab

Все они содержат необходимый набор методов решения математических задач, а также средства для визуализации и отображения полученных результатов. Наиболее известным среди вышеперечисленных программных средств является математический пакет Matlab.

Он позволяет производить различной сложности технические вычисления, содержит одноименный язык программирования, предоставляет большое количество функций анализа данных, связанных практически со всеми областями математики, используется более чем 1 000 000 инженерных работников, поддерживается большинством операционных систем. Однако данный пакет является коммерческим. Разумеется, этот факт затрудняет широкое использование пакета Matlab. Но существуют свободно распространяемые альтернативы данного пакета. В качестве примера можно привести программную систему Scilab.

Scilab – это система компьютерной математики, являющаяся самым полным аналогом пакета Matlab, предназначенная для выполнения научных и инженерных вычислений. В системе Scilab реализованы следующие методы решения вычислительных задач:

— задачи линейной алгебры;

— нелинейные уравнения и системы уравнений;

— обработка экспериментальных данных;

— интегрирование и дифференцирование;

— обыкновенные дифференциальные уравнения и их системы.

Scilab позволяет работать с большим числом специальных функций (Бесселя, Неймана и т.д.), имеет средства для построения и работы с графиками. Для выполнения численных расчётов могут использоваться библиотеки Lapack, LINPACK, Atlas и другие. Для решения нестандартных задач имеется встроенный объектно ориентированный язык программирования, sci-язык, с помощью которого пользователь может создавать свое визуальное приложение в виде отдельной программы. Кроме того, в состав Scilab входит утилита, осуществляющая конвертирование документов из Matlab в Scilab, что немаловажно при разработке программ в системе Scilab, использующих готовые модули пакета Matlab.

Рассмотрим более подробно основные возможности программной системы Scilab при решении различных задач вычислительной математики.

1. Решение задач линейной и нелинейной алгебры.

Система Scilab позволяет решать многие задачи линейной алгебры, к которым относятся операции над матрицами (сложение, вычитание, умножение матриц, умножение матрицы на число, возведение в степень, определение определителя, ранга, ядра матрицы, нормы квадратной матрицы, нахождение обратной и псевдообратной матриц, вычисление собственных значений и собственных векторов квадратной матрицы, треугольное разложение матрицы), решение систем линейных уравнений и др. Также Scilab предоставляет возможность решения задач нелинейной алгебры. Это задачи определения корней полинома, решения трансцендентных уравнений, решения систем нелинейных уравнений. Приведем примеры некоторых задач.

Стандартной задачей линейной алгебры является поиск решения системы линейных уравнений.

Допустим, необходимо найти решение системы линейных уравнений

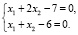
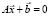
Решение системы линейных уравнений в Scilab осуществляется по команде linsolve (A, b).

A = [1 2; 1 1]; b = [- 7; — 6].

Выполняем команду определения решения системы

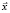
и видим результат – значение вектора :

Безусловно, данная задача является одной из наиболее простых, но первоначальное знакомство с системой Scilab следует осуществлять на подобных задачах.

Рассмотрим задачу LU-разложения матрицы, т.е. представление матрицы А в виде А = C·L·U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка.

Пусть матрица А имеет вид

.

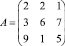
A = [2 -1 5;3 2 -5;1 1 -2].

Выполним команду LU-разложения:

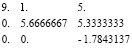
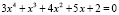
Достаточно распространенным заданием нелинейной алгебры является поиск корней полинома. В качестве примера рассмотрим полином .

Первоначально зададим вектор коэффициентов полинома (в порядке возрастания степеней):

Определим полином р:

.

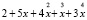
Найдем корни полинома:

X = (0.3788210 + 1.2819084i, 0.3788210 – – 1.2819084i, – 0.5454877 + 0.2748651i, – 0.5454877 – 0.2748651i)

2. Дифференцирование и интегрирование функций.

В системе Scilab реализованы часто применяемые функции численного интегрирования и дифференцирования. Рассмотрим примеры некоторых заданий.

Пусть требуется вычислить значение производной функции f(x) = 2×4 – 8×3 + 8×2 –1 в точке x = 3. Для этого в Scilab реализована команда g = numdiff(fun,x).

Сначала задаем функцию f:

function f = my(x), f = 2*x^4-8*x^3 + + 8*x^2-1, endfunction.

Далее выполняем команду для вычисления производной функции в точке:

Получаем значение производной:

Рассмотрим задачу вычисления определенного интеграла

.

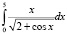
Зададим подынтегральную функцию:

function y = f(x), y = x/sqrt(2 + cos(x)), endfunction.

Запишем команду вычисления определенного интеграла функции на отрезке от 0 до 5:

Значение определенного интеграла равно

Величина ошибки при этом er = 3.264D-09.

3. Дифференциальные уравнения.

В Scilab существует возможность решения обыкновенных дифференциальных уравнений, а также дифференциальных уравнений в частных производных.

Рассмотрим решение дифференциального уравнения

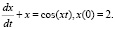
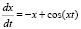
Отсюда .

Определим функцию, содержащуюся в правой части уравнения:

function yd = f(t, x), yd = – x + cos(t*x), endfunction.

Зададим начальное значение х, диапазон значений t.

x0 = 2; t0 = 0; t = 0:1:35.

Найдем решение дифференциального уравнения:

y = ode(x0, t0, t, f).

Построим график найденной функции – решения исходной задачи:

4. Обработка экспериментальных данных.

В системе Scilab реализованы сплайн-интерполяция, метод наименьших квадратов, расчет коэффициентов регрессии и другие функции, используемые для обработки результатов эксперимента.

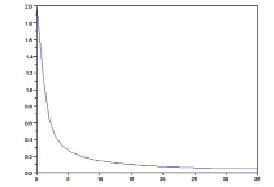
Рис. 1. Графическое решение дифференциального уравнения

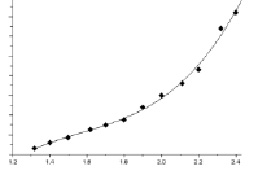
Рис. 2. Графическая интерпретация задачи

Рассмотрим решение задачи построения аналитической зависимости, наиболее точно описывающей результаты экспериментов, методом наименьших квадратов.

Источник: top-technologies.ru

1 Введение

Данный раздел представляет краткий обзор целей создания и основных особенностей пакета Scilab. Здесь мы рассмотрим способы получения и установки дистрибутивов Scilab, основные справочные источники, включая встроенную справочную систему пакета, а также интерактивные демонстрации, поставляемые в составе дистрибутивов.

1.1 О данном руководстве

Данный документ, как и программный продукт, который он описывает, является проектом с открытым исходным кодом. Исходный текст в разметке L A T E X доступен в репозитории Scilab Forge: http://forge.scilab.org/index.php/p/docintrotoscilab/ Исходный текст L A T E X распространяется в соответствии с лицензией Creative Commons Attribution-ShareAlike 3.0 Unported License: http://creativecommons.org/licenses/by-sa/3.0 Скрипты Scilab, используемые в данном руководстве, содержатся в папке scripts проекта. Правила распространения скриптов определяются лицензией CeCiLL: http://www.cecill.info/licences/Licence_CeCILL_V2-en.txt

1.2 Обзор пакета Scilab

Программный пакет Scilab объединяет в себе развитый язык программирования и обширную библиотеку численных алгоритмов, охватывающую многие области научных и технических вычислений. Язык программирования Scilab относится к числу интерпретируемых языков высокого уровня, предоставляя пользователю возможность напрямую манипулировать математическими конструкциями, такими как матрицы или полиномы.

Тем самым достигается большая скорость и простота написания программ. Язык Scilab допускает расширение посредством определения пользовательских типов данных. При этом стандартным операциям, например, арифметическим операторам или операторам сравнения, возможно придать особый смысл применительно к пользовательским типам данных.

Пользователи пакета могут разрабатывать собственные модули расширения для решения конкретных задач. Возможен также вызов из Scilab функций, реализованных на других языках программирования, в частности Fortran или C, благодаря чему сторонние библиотеки могут быть использованы, как если бы они были частью встроенных средств пакета. Scilab также предоставляет возможности для взаимодействия с программным комплексом LabVIEW компании National Instruments, предназначенным для визуального проектирования измерительных систем, а также сбора и анализа экспериментальных данных.

Источник: studfile.net

Scilab

2 декабря, 2013 0

Scilab (читается Сайлэб) – пакет прикладных математических программ для компьютера, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов. Программа Scilab доступна для различных операционных систем, включая Microsoft Windows, Mac OS X и Linux.

Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.

Пакет Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.

Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.

Также Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.

Для численных расчётов используются библиотеки LAPACK, LINPACK, ODEPACK , Automatically Tuned Linear Algebra Software (ATLAS) и другие.

В состав пакета также входит Scicos – инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.

Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Программа имеет открытый исходный код, что позволяет как свободное коммерческое использование и распространение неизменённых версий, так и некоммерческое распространение измененных версий, которые должны включать в себя исходный код. Для коммерческого распространения измёненных версий необходимо согласование с INRIA.

Начиная с версии 5.0 программа распространяется под совместимой с GNU General Public License версии 2 лицензией CeCILL.

С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).

Возможности Scilab

В системе доступно множество инструментов:

• 2D- и 3D-графики, анимация;
• Линейная алгебра, разрежённые матрицы (sparse matrices);
• Полиномиальные и рациональные функции;
• Интерполяция, аппроксимация;
• Симуляция:

гибрид системы моделирования динамических систем и симуляции;

• Дифференциальные и не дифференциальные оптимизации;
• Обработка сигналов;
• Параллельная работа;
• Статистика;
• Работа с компьютерной алгеброй;
• Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW.

Отличительные особенности Scilab

Отличия от некоторых коммерческих программ:

• Бесплатность;
• Свободность (с версии 5.0);
• Маленький размер – дистрибутив 4 версии занимал менее 20 Мб против более чем двухгигабайтного пакета MATLAB.

Инсталлятор 5 версии (5.4.1) увеличился в объёме до 117 Мб;

• Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Microsoft Windows (в UNIX и Microsoft Windows версиях MatLab-а эта возможность присутствует тоже).

Это позволяет производить автоматизированные вычисления, есть пакетный режим.

Ссылки

Источник: wikiprograms.org

Основы программирования в системе Scilab

В Scilab встроен мощный язык программирования с поддержкой объектов. Работа в Scilab может осуществляться как в режиме командной строки, так и в программном режиме. Для создания программы (программу в Scilab иногда называют сценарием) необходимо:

1. Вызвать команду Editorиз меню.

2. В окне редактора Scipadнабрать текст программы.

3. Сохранить текст программы с помощью команды File /Saveв виде файла с расширением sce, например file.sce.

4. После этого программу можно будет вызвать, набрав в командной строке exec, например exec(«file.sce»), или вызвав команду меню File/Exec. или, находясь в окне Scipad, выполнить команду Execute/Load into Scilab(Ctrl+l).

Программный режим достаточно удобен, так как он позволяет сохранить разработанный вычислительный алгоритм в виде файла и повторять его при других исходных данных в других сессиях. Кроме обращений к функциям и операторов присваивания, в программных файлах могут использоваться операторы языка программирования Scilab (язык программирования Scilab будем называть sci-языком).

Основные операторы sci-языка

Функции ввода-вывода в Scilab

Для организации простейшего ввода в Scilab можно воспользоваться функциями

Функция input выводит в командной строке Scilab подсказку title и ждет пока пользователь введет значение, которое в качестве результата возвращается в переменную х.

Функция x_dialog выводит на экран диалоговое окно с именем title, после чего пользователь может щелкнуть OKи тогда stroka вернется в качестве результата в переменную x, либо ввести новое значение вместо stroka, которое и вернется в качестве результата в переменную x.

Набрав вместо strokа число 45 и распечатав х, получим:

Функция input преобразовывает введенное значение к числовому типу данных, а функция x_dialog возвращает строковое значение. Поэтому при использовании функции x_dialog для ввода числовых значений, возвращаемую ею строку следует преобразовать в число с помощью функции evstr. Поэтому можно предложить следующую форму использования функции x_dialog для ввода числовых значений.

x=evstr(x_dialog(‘title’, ‘stroka’));

Можно сразу набрать

->x=evstr(x_dialog(‘title’, ’46’));

Для вывода в текстовом режиме можно использовать функцию disp следующей структуры disp(b). Здесь b — имя переменной или заключенный в кавычки текст.

Оператор присваивания

Оператор присваивания имеет следующую структуру

здесь a – имя переменной или элемента массива, b — значение или выражение. В результате выполнения оператора присваивания переменной a присваивается значение выражения b.

Условный оператор

Одним из основных операторов, реализующим ветвление в большинстве языков программирования, является условный оператор if. Существует обычная и расширенная формы оператора if в Scilab. Обычный if имеет вид

ifЛогическое_выражение then

Else

End

Инструкции в списке разделяют оператором,(запятая)или ;(точка с запятой).

Логические выражения состоят из констант, переменных и функций, соединенных операциями отношения: больше (>), больше или равно (>=), равно (==), не равно (~=) , меньше (), меньше или равно (). Например: x 2 >y. Логические выражения принимают значения «истина» или «ложь». Например, при x=2 и y=8 значение выражения x 2 >y является ложью.

Несколько логических выражений могут быть объединены в одно операторами y | y>7. Если несколько логических выражений соединены оператором if x>5 then y=8, end

—>if x>5 then y=8;t=6; end

2) if Логическое_выражение then Инструкции_1, else Инструкции_2, end

—>if x>5 then y=8,t=6; else y=x^2 ,end

3) if Логическое_выражение then

End

Замечание: слово thenв составе условного оператора ifне является обязательным.

Пример. Вычислить функцию y при x=0.397, если

y=sin(3*x)

y=(2*x – tan(x))./sqrt(x.^2+2)

Набрав этот файл в редакторе Scipad и запустив его на выполнение командой Execute/Load into Scilab, получим:

В качестве примера программирования разветвляющегося процесса рассмотрим решение квадратного уравнения .

Входными данными этой задачи являются коэффициенты квадратного уравнения a, b, c. Выходными данными являются корни уравнения x1 , x2или сообщение о том, что действительных корней нет.

Алгоритм состоит из следующих этапов:

1. Ввод коэффициентов уравнения a, b и с.

2. Проверка, является ли уравнение квадратным (а≠0).

3. Вычисление дискриминанта уравнения d.

4. Если d=0, то выводится сообщение: уравнение имеет два равных корня и печатается значение корня.

5. Если d>0, определяются x1 и x2

Программа решения квадратного уравнения

disp(«Уравнение не является квадратным»)

// Вычисляем дискриминант.

// Если дискриминант отрицателен,

// то вывод сообщения,

disp(‘ Действительных корней нет’);

//иначе-вычисление корней соответствующего

// квадратного уравнения.

disp(«уравнение имеет два равных корня») ;x=-b/(2*a)

Найти все корни квадратного уравнения можно и без оператора if, воспользовавшись тем, что в Scilab определены операции над комплексными числами.

— 1. — 1.4142136i

— 1. + 1.4142136i

Комплексные корни квадратного уравнения

Личность ребенка как объект и субъект в образовательной технологии: В настоящее время в России идет становление новой системы образования, ориентированного на вхождение.

Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас.

Как построить свою речь (словесное оформление): При подготовке публичного выступления перед оратором возникает вопрос, как лучше словесно оформить свою.

Почему 1285321 студент выбрали МегаОбучалку.

Система поиска информации

Источник: megaobuchalka.ru