Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
- s
- r
- c
- r
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, Котангенс
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .
- 90°
- 180°
- 1
- 2
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Онлайн тренажер
для запоминания значений тригонометрических функций для разных углов
Простые тригонометрические тождества
Используя вышеописанные формулы:
Синус, косинус, тангенс, котангенс за 5 МИНУТ
Источник: matematika.club
С какого класса начинается тригонометрия?
С понятиями синус, косинус, тангенс и котангенс учащиеся впервые знакомятся в 8 классе на курсе геометрии (прямоугольный треугольник, теорема Пифагора). Далее, тригонометрия продолжается в программе геометрии 9 класса, и изучается в курсе алгебры (9 класс). Более глубокое изучение предмета продолжается в курсе алгебры и начала анализа — 10 класс. То есть, школьная программа создана специальным образом — постепенное изучение от тригонометрии треугольника к тригонометрическим функциям числового аргумента
9 Нравится Комментировать
Лучший ответ выбран модератором
Другие ответы (9)
- Awerd
- 6. Профи (1945)
- 4 года
Пользователь
Зависит от образовательного учреждения, обычно с 10-го, но есть и с 9-го класса, в редких случаях с 11-го
0 Нравится Комментировать
- Денис
- 7. Мастер (2105)
- 3 года
Пользователь
Сейчас программы в школах очень разные. Почти везде есть отдельные классы с каким-либо уклоном. Конечно, в классах с математическим уклоном тригонометрию раньше начинают осваивать, чем в классах с гуманитарным.
4 Нравится Комментировать
- Эмин Галаев
- 22. Сверхразум (26218)
- 3 года
Пользователь
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
1 Нравится Комментировать
- Иван Глушаков
- 22. Сверхразум (24045)
- 1 год
Пользователь
В девятом классе, на геометрии проходят эту тему (но не углубленно), решают задачи, изучают две теоремы. Синусов и косинусов. Но опять же все зависит от программы, по которой учиться класс. Возможно и в 8 классе пойдут
0 Нравится Комментировать
- Витя Оболенский
- 11. Философ (5965)
- 1 год
Пользователь
Школьники впервые сталкиваются с синусами и косинусами в 8 классе на уроке геометрии. Далее изучают в 9 классе на уроках геометрии, и на уроках алгебры. Самое интересное начинают изучать в 10 классе по полной программе.
3 Нравится Комментировать
- Александра
- 4. Знаток (933)
- 1 год
Пользователь
В 8 классе — как отношения катетов и гипотенузы, потом в 9 классе — как функции угла в градусах, наконец в 10 классе — как функции радиан и чисел со всеми формулами
10 Нравится Комментировать
- Семён
- 22. Сверхразум (34799)
- 1 год
Пользователь
В современной школе первое знакомство с тригонометрией происходит в курсе геометрии 8 класса. Более глубокое изучение предмета продолжается в курсе алгебры 10 класса.
0 Нравится Комментировать
- Ксения Фурманова
- 22. Сверхразум (120298)
- 1 год
Пользователь
Раньше тригонометрия выделялась в отдельный предмет, а сейчас в школьной программе она включена в курс геометрии в 8 классе. На этом этапе происходит первое знакомство, более глубокое изучение предмета продолжается в курсе алгебры в 10 классе.
0 Нравится Комментировать
- Владислав
- 22. Сверхразум (43853)
- 1 месяц
Уже разбираюсь в вашем вопросе!
В Российской Федерации тригонометрия изучается в 10-11 классах школы. Однако в различных странах могут быть различия в том, когда она изучается.
Источник: nolvoprosov.ru
Синус, косинус, тангенс, котангенс

В этом уроке мы покажем связь между синусом, косинусом угла и координатами соответствующих точек единичной полуокружности. Еще раз убедимся в справедливости формулы нахождения тангенса угла через отношение синуса и косинуса этого угла, а также аналогичной формулы для вычисления котангенса угла.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности

1. Откройте доступ ко всем видеоурокам комплекта.

2. Раздавайте видеоуроки в личные кабинеты ученикам.

3. Смотрите статистику просмотра видеоуроков учениками.
Получить доступ
Конспект урока «Синус, косинус, тангенс, котангенс»
В курсе геометрии 8 класса, мы с вами уже знакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Давайте вспомним их.
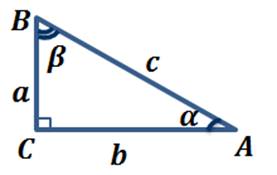
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
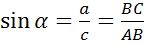
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
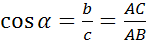
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
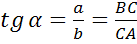 ;
; 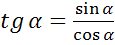
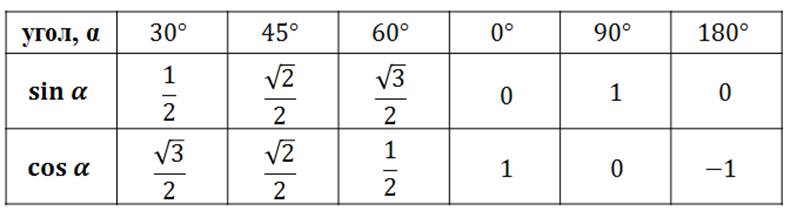
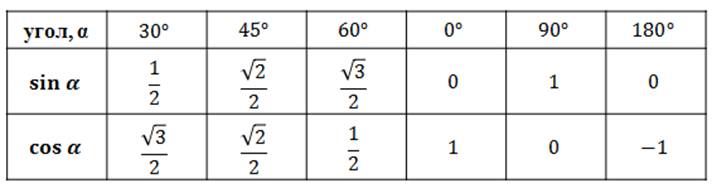
Еще мы с вами учили таблицу синусов, косинусов для углов в 30, 45 и 60 градусов. Давайте вспомним ее.
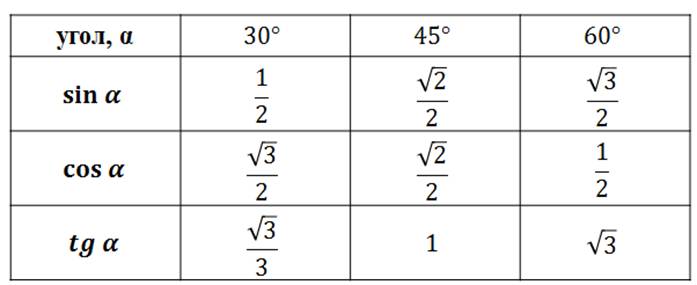
Сегодня на уроке мы познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0 до 180º.
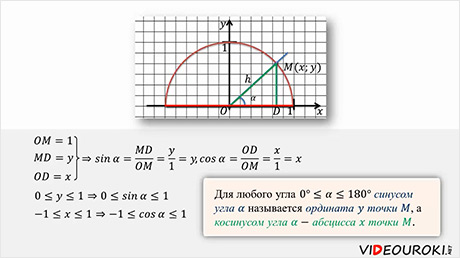
Построим в прямоугольной системе координат полуокружность радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат.
Такую полуокружность мы назовем единичной полуокружностью. Из точки О давайте проведем произвольный луч h. Этот луч пересекает полуокружность с точке М (0;0). Угол между лучом h и положительным направлением оси Ox обозначим за α. Если луч h совпадает с положительным направлением оси Ox, то угол α равен 90º. Если луч h совпадает с осью Oy, то угол α= 90º.
Если луч h совпадает с отрицательным направлением оси Ox, то угол α= 180º. Опустим из точки М перпендикуляр на ось Ox и рассмотрим прямоугольный треугольник ОМD.
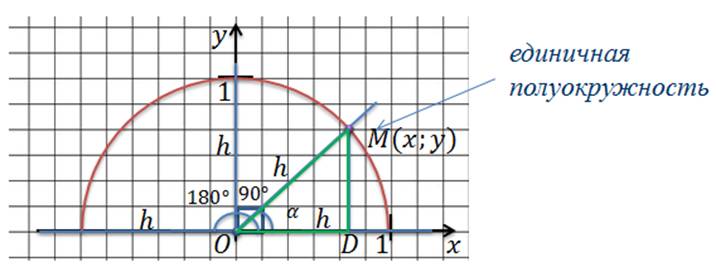
Запишем элементы этого треугольника. Поскольку радиус полуокружности равен 1, значит, ОM=1. Так как координаты точки М равны x и y, то, очевидно, что МD=y, а ОD=x. Тогда 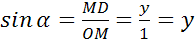
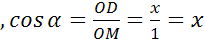 . Мы получили, что синус острого угла равен ординате точки М, а косинус угла α равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.
. Мы получили, что синус острого угла равен ординате точки М, а косинус угла α равен абсциссе точки М. По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.
Для любого угла 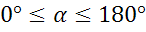 синусом угла
синусом угла 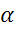 называется ордината
называется ордината 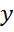 точки
точки 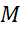 , а косинусом угла
, а косинусом угла 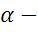 абсцисса
абсцисса 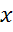 точки
точки 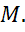
Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменятся от 0 до 1, значит, и синус угла α может принимать значения от 0 до 1. Абсцисса точки М может изменятся от -1 до 1, то есть и косинус угла α из промежутка от 0 до 180º может изменятся от -1 до 1.
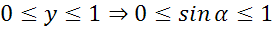
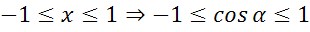
Задача. Может ли:
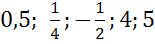
а) абсцисса точки единичной полуокружности быть равна ?
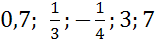
б) ордината точки единичной полуокружности быть равна ?
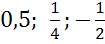
а) Поскольку полуокружность единичная, значит абсцисса точки должны принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна , но не может быть равна 4 и 5.
б) Поскольку полуокружность располагается выше оси Ox, то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината точки может быть равна 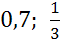 но не может быть равна
но не может быть равна 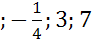 .
.
Дополним известную нам таблицу синусов косинусов:
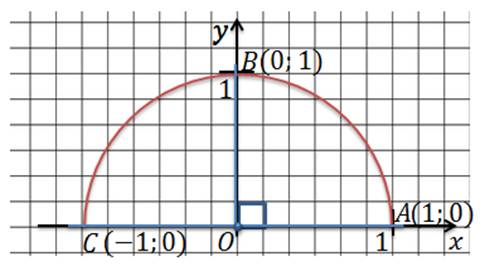
Для определения sin 0º и cos 0º давайте рассмотрим луч ОА. На единичной полуокружности точка А имеет координаты (1;0), значит 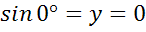 , а
, а 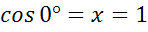 .
.
Найдем теперь значение sin90 º и cos 90º. Этот угол задается лучом ОB. Координаты точки B равны (0;1), значит, 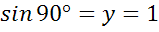 ,
, 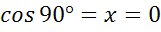 .
.
Проводя аналогичные рассуждения, получим 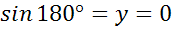 ,
, 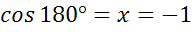 .
.
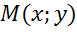
Задача. Определить координаты точки , если:
а) 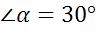 ; б)
; б) 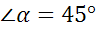 ; в)
; в) 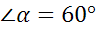 .
.
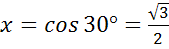
а)
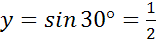
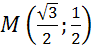
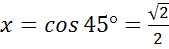
б)
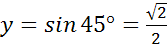
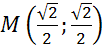
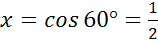
в)
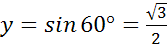
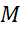
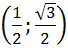
Ответ: 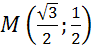 ;
; 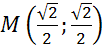 ;
; 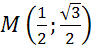 .
.
Решим теперь обратную задачу.
Задача. Определить 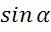 ,
, 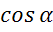 , если:
, если:
а) 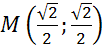 ; б)
; б) 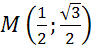 ; в)
; в) 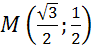 .
.
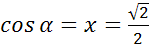
а)
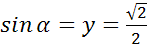
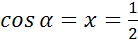
б)
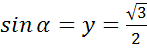
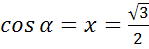
в)
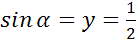
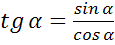
Тангенсом острого угла мы называли отношение
. Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 90º, то его cos 90º=0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы немного уточнили определение тангенса.
Тангенсом угла 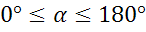 ,
, 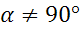 называется
называется 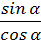 .
.
Котангенсом острого угла мы называли отношение 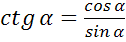 . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то sin равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому
. Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то sin равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому 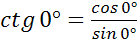 ,
, 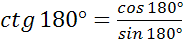 – не существует. Таким образом, мы немного уточнили определение котангенса.
– не существует. Таким образом, мы немного уточнили определение котангенса.
Котангенсом угла 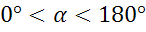 , называется
, называется 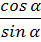 .
.
Задача. Определить 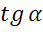 ,
, 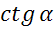 , если:
, если:
а) 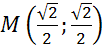 ; б)
; б) 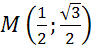 ; в)
; в) 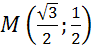 ; г)
; г) 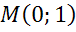 ; д)
; д) 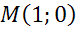 .
.
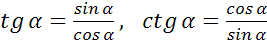
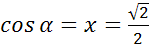
а)
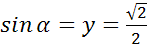
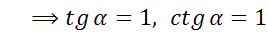
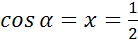
б)
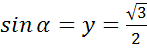
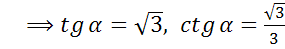
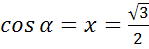
в)
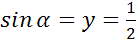
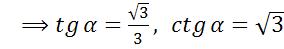
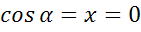
г)
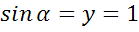
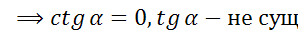
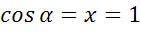
д)
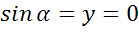
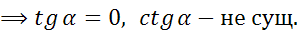
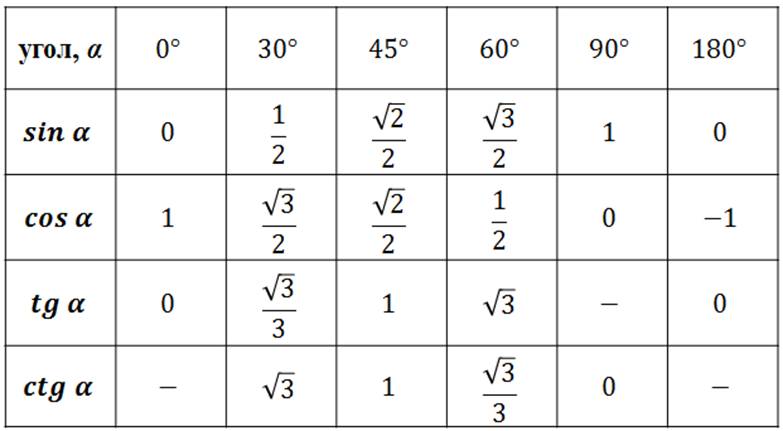
Давайте занесем полученные данные в таблицу и составим таблицу синусов, косинусов, тангенсов и котангенсов для углов 0º, 30º, 45º, 60º, 90º, 180º.
Подведем итоги урока. Сегодня на уроке мы определили, что Для любого угла 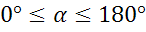 синусом угла
синусом угла 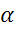 называется ордината
называется ордината 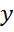 точки
точки 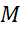 , а косинусом угла
, а косинусом угла 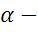 абсцисса
абсцисса 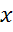 точки
точки 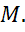
Тангенсом угла 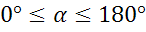 ,
, 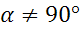 называется
называется 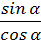 .
.
Котангенсом угла 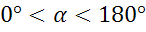 , называется
, называется 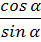 .
.
Также мы дополнили известную нам таблицу значений синуса, косинуса и тангенсов для некоторых углов.
Источник: videouroki.net