Симплекс метод код программы

Пользователь

: 68

Симплекс метод на с++ или на си#.

Всем Добрый день!
Мне нужно написать программу ,вычисляющую
L = 6 x1 + 5 x2 + 9 x3
при следующих ограничениях
5 x1 + 2×2 + 3 x3 x1 + 6 x2 + 2 x3 4 x1 + 3 x3 Помогите,пожалуйста.

Нет,не блондинка!!

Пользователь

: 68

Ураааа)))Я решила))))чудо свершилось))

#include using namespace std; int main () < int n, k, st,sv ; int i = 0, j = 0; double **mas; setlocale (LC_CTYPE, «rus»); cout > st; //Число строк n=st+1; cout >sv; //Число столбцов k=sv+n; mas = new double*[n]; //Выделение памяти под n-строк for(i = 0; i < n; i++) < mas[i] = new double[k]; //Выделение памяти для каждой строки по k-столбцов >for(i = 0; i < n; i++) < if (i> mas[i][j]; > > //вывод массива cout cout cout<0) kpol++; > // coutr) myn=i; > cout cout cout //из элеметов соответствующих строк вычитаем элементы найденной нам строки double p=0; for(i = 0; i < n; i++) < p=mas[i][min]; if (i!=myn) < for(j = 0; j < k; j++) < mas[i][j]=mas[i][j]-mas[myn][j]*p; >> > //вывод массива cout <cout cout<0) kpol++; > // cout cout

Нет,не блондинка!!

Симплекс метод в Python. Библиотеки: Numpy. Scipy. #симплексметод, #python, #numpy, #scipy

Последний раз редактировалось Аделинкка; 18.06.2012 в 04:41 .

Источник: www.programmersforum.ru

Подробный разбор симплекс-метода

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

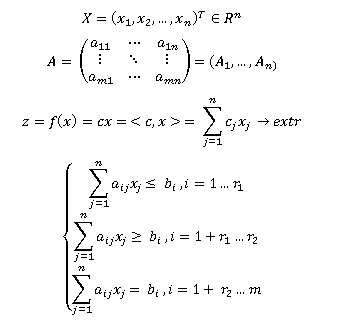
§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

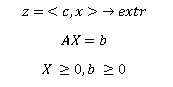
Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Решение задачи линейного программирования при помощи надстройки Поиск решения

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

• Если , то
• Если — любой, то , где

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

§4. Симплекс-метод

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:

1. Задача должна иметь каноническую форму.
2. У задачи должен быть явно выделенный базис.

Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

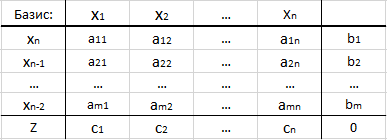
• В первой строке указывают «наименование» всех переменных.
• В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
• В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
• Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
• Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

Замечание: Коэффициенты в строке функционала берутся со знаком “-”.

Алгоритм симплекс-метода:

1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

• Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
• Если задача на максимум – выбираем минимальный отрицательный.

Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

• Вектор правых частей почленно делится на ведущий столбец
• Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

Определение: Такой элемент называется ведущим элементом.

4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

• Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
• Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

§5. Интерпретация результата работы симплекс-метода

1. Оптимальность

Условие оптимальности полученного решения:

• Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
• Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

3. Альтернативные решения

При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

Алгебраический признак существования альтернативы:

После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

Эпилог

Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

Спасибо за внимание!

Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

• Математика
• Линейное программирование
• Симплекс-метод
• Оптимизация

Источник: habr.com

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

Симплекс-метод. Реализация

В этой статье рассматривается симплекс-метод, который применяется при решении задач линейного программирования (ЗЛП). Приводится алгоритм метода, а также его реализация на языке C#. Реализация представлена в конце статьи.

Определения

Симплекс-метод — это алгоритм, используемый при решении оптимизационной задачи линейного программирования.

Линейное программирование — это раздел математики, занимающийся решением экстремальных задач (нахождением экстремума функции) на множестве пространства, заданном системой линейных уравнений и неравенств.

Оптимизация — задача нахождения минимума или максимума (экстремума) целевой функции.

Целевая функция — это функция нескольких переменных, подлежащая оптимизации в целях решения какой-либо оптимизационной задачи (например, задачи объемного планирования).

Алгоритм симплекс-метода

В начале исходную задачу линейного программирования приводят к каноническому виду, затем составляют симплекс-таблицу вида:

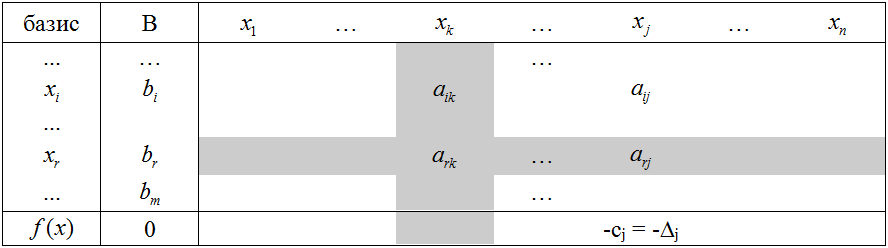
где в столбце «базис» указываются базисные переменные, а в последней строке столбца «базис» пишется f(x). В столбец «B» записываются свободные члены ограничений bi и значение целевой функции (на 1-м этапе оно равно 0, т.е. никакой прибыли).

В столбцах xj для не базисных переменных указываются коэффициенты при не базисных переменных из ограничений задачи. В столбцах базисных переменных содержится только 0 или 1 на пересечении столбца с соответствующей строкой базисной переменной.

В последней строке -cj — это коэффициенты при переменных целевой функции взятые с противоположным знаком.

Симплекс-таблица составлена, теперь опишем сам симплекс-метод.

Шаг 1: Выполняется проверка полученного базисного плана на оптимальность по условию: если при каком-либо ДБР (допустимое базисное решение) в симплекс-таблице все коэффициенты строки f(x) (то есть -cj) не отрицательны, то данное ДБР оптимально, следовательно КОНЕЦ решения. В противном случае:

Шаг 2: Переход к новому базисному плану. Для этого из числа небазисных переменных с отрицательными значениями в последней строке (то есть -cj < 0) выбирается переменная, вводимая в базис — xk, это переменная которой соответствует наибольшая по модулю отрицательная оценка:

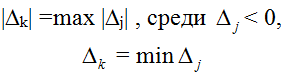
Столбец, отвечающий переменной xk, называется главным, или ведущим. Элементы данного столбца обозначаются через aik.

Если окажется несколько одинаковых наибольших по модулю отрицательных оценок, то выбирается любая из соответственных переменных.

Шаг 3: Выбираем переменную r — переменную, которая выводится из базиса. Данная переменная находится из соотношения:

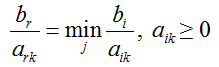
Строка таблицы, в которой получено наименьшее отношение элемента столбца «В» к соответствующему положительному элементу ведущего столбца, является ведущей, или главной.

Элементы главной строки обозначаются через arj. Выбранная переменная xr будет выводиться из базиса, то есть это исключаемая переменная.

Если окажется несколько одинаковых наименьших значений отношений, то выбирается любая из соответствующих им переменных.

Элемент, который стоит на пересечении главного столбца и строки называется главным, или ведущим, и обозначается ark.

Шаг 4: Для определения нового базисного плана проводится пересчет элементов симплекс-таблицы, и результаты заносятся в новую таблицу. Выбранные переменные среди базисных и не базисных, лежащих на главной строке и главном столбце, меняются местами.

Процедура пересчета элементов выполняется следующим образом:

а) элементы главной строки необходимо разделить на ведущий элемент:

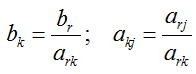
б) элементы полученной строки умножаются на -aik, и результаты складываются с i-той строкой, причем i ≠ k:

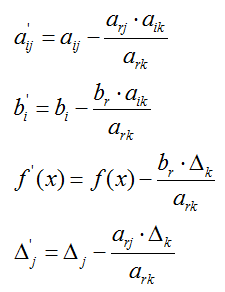
После определения новой симплекс-таблицы переходят к шагу 1.

Симплекс-метод. Реализация C#

Приводим программную реализацию симплекс-метода. Программа написана на языке программирования C#.

Важная информация! Пожалуйста прочтите!

Входные данные: симплекс-таблица без базисных переменных в столбцах. То есть таблица должна быть построена только по коэффициентам при переменных из ограничений задачи и целевой функции.

Формат входных данных: двумерный массив из элементов типа double.

Входные данные передаются в качестве аргумента, при создании экземпляра класса Simplex.

При вызове метода Calculate в качестве аргумента вы должны передать одномерный массив из элементов типа double, длиной в количество переменных в целевой функции. В этот массив будут записаны найденные значения неизвестных.

Выходные данные: метод Calculate возвращает ссылку на двумерный массив, содержащий решенную симплекс-таблицу. Кроме того решение будет занесено в массив, переданный в качестве аргумента в метод Calculate.

Формат выходных данных: двумерный массив из элементов типа double и одномерный массив из элементов типа double.

Источник: vscode.ru