Scipy что это за программа

Учебник Python SciPy

В этом уроке мы увидим, как используется библиотека SciPy в Python и как она помогает нам работать с математическими уравнениями и алгоритмами в интерактивном режиме. Хорошая вещь в пакете SciPy Python заключается в том, что если мы хотим классы или создавать веб-страницы, SciPy полностью совместим с системой в целом и может обеспечить бесшовную интеграцию.

В виде SciPy с открытым исходным кодом, у него очень активное и яркое сообщество разработчиков, благодаря которому существует огромное количество модулей для огромного количества научных приложений и вычислений, доступных с SciPy. Вот некоторые из сложных математических операций, которые можно выполнять с помощью SciPy:

• Интерполяция
• Интеграция
• Оптимизация
• Обработка изображений
• Статистика
• Расчеты специальных функций и т. Д.

SciPy можно сравнить с большинством командных и стандартных библиотек, таких как библиотека GSL для C ++ и Matlab. Поскольку SciPy построен поверх пакета NumPy, эти два пакета также могут быть полностью интегрированы. Если вы можете придумать математическую операцию, которую необходимо выполнить, убедитесь, что вы проверили библиотеку SciPy, прежде чем реализовывать этот модуль самостоятельно, потому что в большинстве случаев SciPy уже полностью реализовал все операции для вас.

Где используется язык Python || Области и сферы применения языка python

Установить библиотеку SciPy

Давайте установим библиотеку SciPy, прежде чем мы перейдем к реальным примерам и концепциям. Есть два способа установить этот пакет. Первый включает использование диспетчера пакетов Python, pip:

pip install scipy

Второй способ относится к Anaconda, мы можем установить пакет как:

conda install -c anaconda scipy

После установки библиотеки мы можем импортировать ее как:

Наконец, поскольку мы также будем использовать NumPy (рекомендуется, чтобы для всех операций NumPy мы использовали NumPy напрямую, а не через пакет SciPy):

Возможно, что в некоторых случаях нам также захочется отобразить наши результаты, для чего мы будем использовать библиотеку Matplotlib. Выполните следующий импорт для этой библиотеки:

Я буду использовать менеджер Anaconda для всех примеров в этом уроке. Я запущу Jupyter Notebook для того же:

Теперь, когда мы готовы со всеми операторами импорта для написания некоторого кода, давайте начнем погружаться в пакет SciPy с некоторыми практическими примерами.

Работа с полиномиальными уравнениями

Мы начнем с рассмотрения простых полиномиальных уравнений. Есть два способа интегрировать полиномиальные функции в нашу программу. Мы можем использовать poly1d класс, который использует коэффициенты или корни многочлена для инициализации многочлена. Давайте посмотрим на пример:

из numpy import poly1d
first_polynomial = poly1d ([3, 4, 7])
печать (первое_полином)

Основы SciPy | Научные И Математические Вычисления На Python

Когда мы запустим этот пример, мы увидим следующий результат:

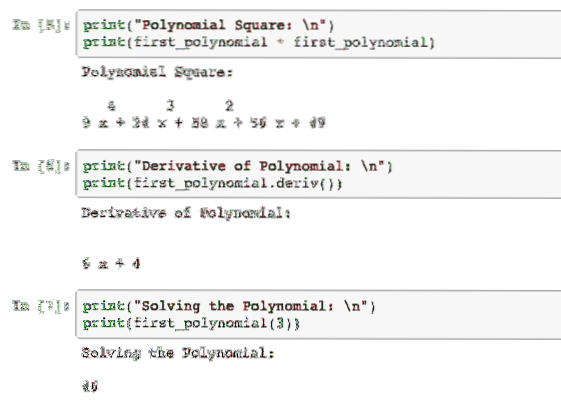
Ясно, что полиномиальное представление уравнения печатается как результат, так что результат довольно легко понять. Мы также можем выполнять различные операции с этим многочленом, например возводить его в квадрат, находить его производную или даже решать его для значения x. Попробуем сделать все это в следующем примере:

print («Полиномиальный квадрат: n»)
print (первый_полином * первый_полином)
print («Производная многочлена: n»)
print (first_polynomial.производная ())
print («Решение многочлена: n»)
печать (первый_полином (3))

Когда мы запустим этот пример, мы увидим следующий результат:

Когда я подумал, что это все, что мы можем сделать с помощью SciPy, я вспомнил, что мы также можем интегрировать полином. Давайте запустим последний пример с полиномами:

print («Интегрирование полинома: n»)
print (first_polynomial.интег (1))

Передаваемое целое число сообщает пакету, сколько раз нужно интегрировать полином:

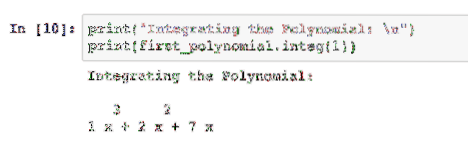
Мы можем просто передать другое целое число, которое сообщает пакету, сколько раз нужно интегрировать этот многочлен.

Решение линейных уравнений

С помощью SciPy можно даже решать линейные уравнения и находить их корни, если они существуют. Для решения линейных уравнений мы представляем набор уравнений в виде массивов NumPy, а их решение — в виде отдельных массивов NumPy. Давайте визуализируем это на примере, где мы делаем то же самое и используем линалг пакет, чтобы найти корни уравнений, вот уравнения, которые мы будем решать:

1x + 5y = 6
3х + 7у = 9

Решим приведенные выше уравнения:

от scipy import linalg
уравнение = np.массив ([[1, 5], [3, 7]])
решение = np.массив ([[6], [9]])
корни = linalg.решить (уравнение, решение)
print («Нашел корни:»)
печать (корни)
print (» n Точечное произведение должно быть равно нулю, если решения верны:»)
печать (уравнение.точка (корни) — решение)

Когда мы запустим вышеуказанную программу, мы увидим, что уравнение скалярного произведения дает нулевой результат, что означает, что корни, найденные программой, были правильными:

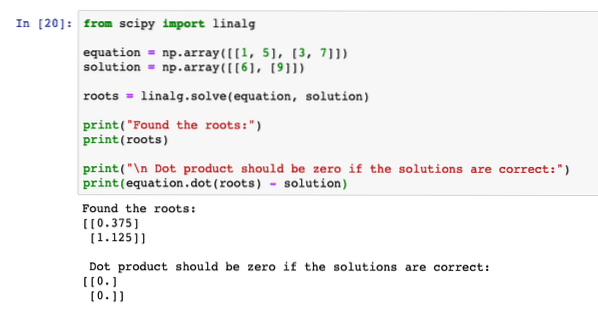
Преобразования Фурье с помощью SciPy

Преобразования Фурье помогают нам выразить функцию как отдельные компоненты, составляющие эту функцию, и направляют нас в отношении того, как мы можем рекомбинировать эти компоненты, чтобы вернуть исходную функцию.

Давайте посмотрим на простой пример преобразования Фурье, где мы строим сумму двух косинусов с помощью библиотеки Matplotlib:

из scipy.fftpack import fft
# Количество точек выборки
N = 500
# образец интервала
Т = 1.0/800.0
х = np.linspace (0.0, Н * Т, Н)
y = np.cos (50.0 * 2.0 * нп.пи * х) + 0.5 * нп.cos (80.0 * 2.0 * нп.пи * х)
yf = fft (y)
xf = np.linspace (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib для построения графиков
импортировать matplotlib.pyplot как plt
plt.сюжет (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.title (‘Информация’)
plt.ylabel (‘ось Y’)
plt.xlabel (‘ось X’)
plt.сетка()
plt.показывать()

Здесь мы начали с построения образца пространства и уравнения косинуса, которое затем преобразовали и построили. Вот результат работы вышеуказанной программы:

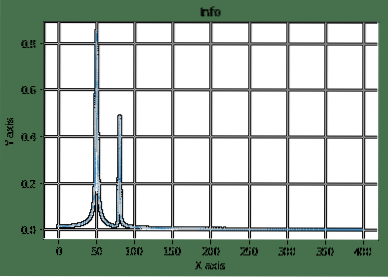
Это один из хороших примеров, когда мы видим, как SciPy используется в сложном математическом уравнении, чтобы легко визуализировать вещи.

Векторы и матрица с SciPy

Теперь, когда мы знаем многое, на что способен SciPy, мы можем быть уверены, что SciPy также может работать с векторами и матрицами. Матрицы являются важной частью линейной алгебры, поскольку матрицы — это то, что мы также используем для представления векторных отображений.

Так же, как мы рассматривали решение линейных уравнений с помощью SciPy, мы можем представить векторы с помощью нп.множество() функции. Начнем с построения матрицы:

my_matrix = np.матрица (np.случайный.случайный ((3, 3)))
печать (my_matrix)

Вот результат приведенного выше фрагмента:

Когда мы говорим о матрицах, мы всегда говорим о собственных значениях и собственных векторах. Проще говоря, собственные векторы — это векторы, которые при умножении на матрицу не меняют своего направления, в отличие от большинства векторов. Это означает, что даже когда вы умножаете собственные векторы на матрицу, существует значение (или собственное значение), которое является одним из факторов умножения. Это означает:

В приведенном выше уравнении A — матрица, λ — собственное значение, а x — вектор. Напишем простой фрагмент кода, чтобы найти собственные значения для данного вектора:

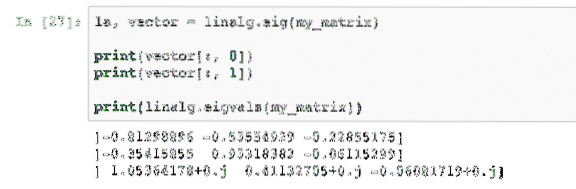
la, vector = linalg.eig (my_matrix)
печать (вектор [:, 0])
печать (вектор [:, 1])
печать (линалг.eigval (my_matrix))

Когда мы запустим этот пример, мы увидим следующий результат:

Вычисление определителя матрицы

Следующая операция, которую мы выполним с SciPy, — это вычисление определителя 2-мерной матрицы. Мы будем повторно использовать матрицу, которую мы использовали в последнем фрагменте кода, здесь:

Когда мы запустим этот пример, мы увидим следующий результат:

Заключение

В этом уроке мы рассмотрели множество хороших примеров, в которых SciPy может помочь нам, выполняя сложные математические вычисления за нас с помощью простого в использовании API и пакетов.

Мышь

Пользователи планшетов часто пропускают указатель мыши, особенно когда они привыкли пользоваться ноутбуками. Смартфоны и планшеты с сенсорным экраном .

Мышь

В средняя кнопка мыши помогает пролистывать длинные веб-страницы и экраны с большим объемом данных. Если это прекратится, вы в конечном итоге будете и.

Мышь

Совершенно нормально, что все устройства компьютерной мыши эргономичны для правшей. Но есть мышиные устройства, специально разработанные для левшей ил.

Свежие статьи об операционных системах. Множество интересных гайдов и полезных советов. Почувствуйте себя своим в мире современных технологий

Источник: ru.phen375questions.com

Библиотека SciPy в Python

Библиотека Python SciPy – это набор удобных функций, построенных на NumPy и математических алгоритмах.

• В настоящее время библиотека SciPy поддерживает интеграцию, градиентную оптимизацию, специальные функции, средства решения обыкновенных дифференциальных уравнений, инструменты параллельного программирования и многое другое. Другими словами, мы можем сказать, что если что-то есть в общем учебнике числовых вычислений, высока вероятность того, что вы найдете его реализацию в SciPy.
• Интерактивный сеанс с SciPy – это, по сути, среда обработки данных и прототипирования системы, такая же, как MATLAB, Octave, Scilab или R-lab.
• SciPy – это проект с открытым исходным кодом, выпущенный под лицензией BSD.

Почему SciPy?

SciPy предоставляет высокоуровневые команды и классы для управления данными и визуализации данных, что значительно увеличивает мощность интерактивного сеанса Python.

Помимо математических алгоритмов в SciPy, программисту доступно все, от классов, веб-подпрограмм и баз данных до параллельного программирования, что упрощает и ускоряет разработку сложных и специализированных приложений.

Поскольку SciPy имеет открытый исходный код, разработчики по всему миру могут вносить свой вклад в разработку дополнительных модулей, что очень полезно для научных приложений, использующих SciPy.

Установка библиотеки SciPy

Мы обсудим некоторые основные функции и важные особенности SciPy, но перед установкой SciPy. Мы можем установить пакеты SciPy, просто используя pip, выполните следующую команду в терминале (добавьте sudo, если необходимо):

pip install scipy

Чтобы установить этот пакет с помощью conda run:

conda install -c anaconda scipy

Импорт

Чтобы начать использовать Scipy в наших проектах python, мы просто импортируем Scipy как:

import scipy

Взаимодействие с Numpy

Как мы уже знаем, SciPy построен на NumPy, поэтому для всех основных нужд мы можем использовать сами функции NumPy:

import numpy

Функции из numpy и numpy.lib.scimath также содержатся в SciPy, но рекомендуется использовать их напрямую, а не проходить через SciPy в этом случае.

Работа с polynomial

В SciPy есть два способа работы с polynomial. Первый использует класс poly1d. Этот класс принимает коэффициенты или корни для инициализации и формирует полиномиальный объект. Когда мы печатаем этот объект, мы видим, что он напечатан, как polynomial. Давайте посмотрим на пример кода:

from numpy import poly1d # We’ll use some functions from numpy remember!! # Creating a simple polynomial object using coefficients somePolynomial = poly1d([1,2,3]) # Printing the result # Notice how easy it is to read the polynomial this way print(somePolynomial) # Let’s perform some manipulations print(«nSquaring the polynomial: n») print(somePolynomial* somePolynomial) #How about integration, we just have to call a function # We just have to pass a constant say 3 print(«nIntegrating the polynomial: n») print(somePolynomial.integ(k=3)) #We can also find derivatives in similar way print(«nFinding derivative of the polynomial: n») print(somePolynomial.deriv()) # We can also solve the polynomial for some value, # let’s try to solve it for 2 print(«nSolving the polynomial for 2: n») print(somePolynomial(2))

Другой способ работы с polynomial – использовать массив коэффициентов. Существуют функции, доступные для выполнения операций с polynomial, представленными в виде последовательностей, первый метод выглядит намного проще в использовании и дает вывод в удобочитаемой форме, поэтому я предпочитаю первый для примера.

Линейная алгебра

SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.

Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.

Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.

Этот метод ожидает входную матрицу и вектор правой части:

# Import required modules/ libraries import numpy as np from scipy import linalg # We are trying to solve a linear algebra system which can be given as: # 1x + 2y =5 # 3x + 4y =6 # Create input array A= np.array([[1,2],[3,4]]) # Solution Array B= np.array([[5],[6]]) # Solve the linear algebra X= linalg.solve(A,B) # Print results print(X) # Checking Results print(«n Checking results, following vector should be all zeros») print(A.dot(X)-B)

Интеграция SciPy

Подпакет интеграции scipy предоставляет различные методы интеграции. Мы можем посмотреть на них, просто набрав:

help(integrate)

Попробуем интегрировать лямбда функцию в скрипт:

# Import required packages from scipy import integrate # Using quad as we can see in list quad is used for simple integration # arg1: A lambda function which returns x squared for every x # We’ll be integrating this function # arg2: lower limit # arg3: upper limit result= integrate.quad(lambda x: x**2, 0,3) print(result)

Преобразование Fourier

Анализ Fourier помогает нам выразить функцию, как сумму периодических компонентов и восстановить сигнал из этих компонентов.

Давайте посмотрим на простой пример преобразования Fourier. Мы будем строить сумму двух синусов:

# Import Fast Fourier Transformation requirements from scipy.fftpack import fft import numpy as np # Number of sample points N = 600 # sample spacing T = 1.0 / 800.0 x = np.linspace(0.0, N*T, N) y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x) yf = fft(y) xf = np.linspace(0.0, 1.0/(2.0*T), N//2) # matplotlib for plotting purposes import matplotlib.pyplot as plt plt.plot(xf, 2.0/N * np.abs(yf[0:N//2])) plt.grid() plt.show()

Специальные функции

В специальном подпакете SciPy есть определения множества функций математической физики. Доступны следующие функции: эри, Бессель, бета, эллиптическая, гамма, гипергеометрическая, Кельвина, Матье, параболический цилиндр, сфероидальная волна и струве. Давайте посмотрим на функцию Бесселя.

Функции Бесселя – это семейство решений дифференциального уравнения Бесселя с вещественным или комплексным порядком альфа.

Давайте лучше рассмотрим это на примере, пример представляет собой круглый барабан, закрепленный на краю:

# Import special package from scipy import special import numpy as np def drumhead_height(n, k, distance, angle, t): kth_zero = special.jn_zeros(n, k)[-1] return np.cos(t) * np.cos(n*angle) * special.jn(n, distance*kth_zero) theta = np.r_[0:2*np.pi:50j] radius = np.r_[0:1:50j] x = np.array([r * np.cos(theta) for r in radius]) y = np.array([r * np.sin(theta) for r in radius]) z = np.array([drumhead_height(1, 1, r, theta, 0.5) for r in radius]) # Plot the results for visualization import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm fig = plt.figure() ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(‘X’) ax.set_ylabel(‘Y’) ax.set_zlabel(‘Z’) plt.show()

Некоторые функции, такие как функция бинарной энтропии, функция шага Хевисайда и функция линейного изменения, легко реализовать с помощью существующих функций NumPy и SciPy и, следовательно, не включены в этот пакет.

Вывод

В этом посте мы разобрали библиотеку SciPy в Python для простых и эффективных математических операций.

Мы узнали, что это обширная библиотека, используемая для разработки научных приложений, и в которой необходимо выполнять сложные математические операции, например, в машинном или глубоком обучении. Мы также узнали, как пакет scipy помогает нам в выполнении различных математических операций.

Источник: pythonim.ru

scipy 1.9.3

SciPy (pronounced “Sigh Pie”) is an open-source software for mathematics, science, and engineering. It includes modules for statistics, optimization, integration, linear algebra, Fourier transforms, signal and image processing, ODE solvers, and more.

• Website:https://scipy.org
• Documentation:https://docs.scipy.org/
• Mailing list:https://mail.python.org/mailman3/lists/scipy-dev.python.org/
• Source code:https://github.com/scipy/scipy
• Contributing:https://scipy.github.io/devdocs/dev/index.html
• Bug reports:https://github.com/scipy/scipy/issues
• Code of Conduct:https://scipy.github.io/devdocs/dev/conduct/code_of_conduct.html
• Report a security vulnerability:https://tidelift.com/docs/security
• Citing in your work:https://www.scipy.org/citing-scipy/

SciPy is built to work with NumPy arrays, and provides many user-friendly and efficient numerical routines, such as routines for numerical integration and optimization. Together, they run on all popular operating systems, are quick to install, and are free of charge. NumPy and SciPy are easy to use, but powerful enough to be depended upon by some of the world’s leading scientists and engineers. If you need to manipulate numbers on a computer and display or publish the results, give SciPy a try!

For the installation instructions, see our install guide.

Call for Contributions

We appreciate and welcome contributions. Small improvements or fixes are always appreciated; issues labeled as “good first issue” may be a good starting point. Have a look at our contributing guide.

Writing code isn’t the only way to contribute to SciPy. You can also:

• review pull requests
• triage issues
• develop tutorials, presentations, and other educational materials
• maintain and improve our website
• develop graphic design for our brand assets and promotional materials
• help with outreach and onboard new contributors
• write grant proposals and help with other fundraising efforts

If you’re unsure where to start or how your skills fit in, reach out! You can ask on the mailing list or here, on GitHub, by leaving a comment on a relevant issue that is already open.

If you are new to contributing to open source, this guide helps explain why, what, and how to get involved.

Источник: pypi.org

SciPy, оптимизация

SciPy (произносится как сай пай) — это пакет прикладных математических процедур, основанный на расширении Numpy Python. С SciPy интерактивный сеанс Python превращается в такую же полноценную среду обработки данных и прототипирования сложных систем, как MATLAB, IDL, Octave, R-Lab и SciLab. Сегодня я хочу коротко рассказать о том, как следует применять некоторые известные алгоритмы оптимизации в пакете scipy.optimize. Более подробную и актуальную справку по применению функций всегда можно получить с помощью команды help() или с помощью Shift+Tab.

Введение

Дабы избавить самого себя и читателей от поиска и чтения первоисточников, ссылки на описания методов будут в основном на википедию. Как правило, этой информации достаточно для понимания методов в общих чертах и условий их применения. Для понимания сути математических методов идем по ссылкам на более авторитетные публикации, которые можно найти в конце каждой статьи или в любимой поисковой системе.

Итак, модуль scipy.optimize включает в себя реализацию следующих процедур:

1. Условной и безусловной минимизации скалярных функций нескольких переменных (minim) с помощью различных алгоритмов (симплекс Нелдера-Мида, BFGS, сопряженных градиентов Ньютона, COBYLA и SLSQP)
2. Глобальной оптимизации (например: basinhopping, diff_evolution)
3. Минимизация остатков МНК (least_squares) и алгоритмы подгонки кривых нелинейным МНК (curve_fit)
4. Минимизации скалярной функций одной переменной (minim_scalar) и поиска корней (root_scalar)
5. Многомерные решатели системы уравнений (root) с использованием различных алгоритмов (гибридный Пауэлла, Левенберг-Марквардт или крупномасштабные методы, такие как Ньютона-Крылова).

В этой статье мы рассмотрим только первый пункт из всего этого списка.

Безусловная минимизация скалярной функции нескольких переменных

Функция minim из пакета scipy.optimize предоставляет общий интерфейс для решения задач условной и безусловной минимизации скалярных функций нескольких переменных. Чтобы продемонстрировать ее работу, нам понадобится подходящая функция нескольких переменных, которую мы будем по-разному минимизировать.

Для этих целей прекрасно подойдет функция Розенброка от N переменных, которая имеет вид:

Несмотря на то, что функция Розенброка и ее матрицы Якоби и Гессе (первой и второй производной соответственно) уже определены в пакете scipy.optimize, определим ее самостоятельно.

import numpy as np def rosen(x): «»»The Rosenbrock function»»» return np.sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0, axis=0)

Для наглядности отрисуем в 3D значения функции Розенброка от двух переменных.

Код для отрисовки

from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt from matplotlib import cm from matplotlib.ticker import LinearLocator, FormatStrFormatter # Настраиваем 3D график fig = plt.figure(figsize=[15, 10]) ax = fig.gca(projection=’3d’) # Задаем угол обзора ax.view_init(45, 30) # Создаем данные для графика X = np.arange(-2, 2, 0.1) Y = np.arange(-1, 3, 0.1) X, Y = np.meshgrid(X, Y) Z = rosen(np.array([X,Y])) # Рисуем поверхность surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm) plt.show()

Зная заранее, что минимум равен 0 при , рассмотрим примеры того, как определить минимальное значение функции Розенброка с помощью различных процедур scipy.optimize.

Симплекс-метод Нелдера-Мида (Nelder-Mead)

Пусть имеется начальная точка x0 в 5-мерном пространстве. Найдем ближайшую к ней точку минимума функции Розенброка с помощью алгоритма симплекса Nelder-Mead (алгоритм указан в качестве значения параметра method):

from scipy.optimize import minimize x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2]) res = minimize(rosen, x0, method=’nelder-mead’, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 339 Function evaluations: 571 [1. 1. 1. 1. 1.]

Симплекс-метод является самым простым способом свести к минимуму явно определенную и довольно гладкую функцию.

Он не требует вычисления производных функции, достаточно задать только ее значения. Метод Нелдера-Мида является хорошим выбором для простых задач минимизации. Однако, поскольку он не использует оценки градиента, для поиска минимума может потребоваться больше времени.

Метод Пауэлла

Другим алгоритмом оптимизации, в котором вычисляются только значения функций, является метод Пауэлла. Чтобы использовать его, нужно установить method = ‘powell’ в функции minim.

x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2]) res = minimize(rosen, x0, method=’powell’, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 19 Function evaluations: 1622 [1. 1. 1. 1. 1.]

Алгоритм Бройдена-Флетчера-Голдфарба-Шанно (BFGS)

Для получения более быстрой сходимости к решению, процедура BFGS использует градиент целевой функции. Градиент может быть задан в виде функции или вычисляться с помощью разностей первого порядка. В любом случае, обычно метод BFGS требует меньше вызовов функций, чем симплекс-метод.

Найдем производную от функции Розенброка в аналитическом виде:

Это выражение справедливо для производных всех переменных, кроме первой и последней, которые определяются как:

Посмотрим на функцию Python, которая вычисляет этот градиент:

def rosen_der (x): xm = x [1: -1] xm_m1 = x [: — 2] xm_p1 = x [2:] der = np.zeros_like (x) der [1: -1] = 200 * (xm-xm_m1 ** 2) — 400 * (xm_p1 — xm ** 2) * xm — 2 * (1-xm) der [0] = -400 * x [0] * (x [1] -x [0] ** 2) — 2 * (1-x [0]) der [-1] = 200 * (x [-1] -x [-2] ** 2) return der

Функция вычисления градиента указывается в качестве значения параметра jac функции minim, как показано ниже.

res = minimize(rosen, x0, method=’BFGS’, jac=rosen_der, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 25 Function evaluations: 30 Gradient evaluations: 30 [1.00000004 1.0000001 1.00000021 1.00000044 1.00000092]

Алгоритм сопряженных градиентов (Ньютона)

Алгоритм сопряженных градиентов Ньютона является модифицированным методом Ньютона.
Метод Ньютона основан на аппроксимации функции в локальной области полиномом второй степени:

где является матрицей вторых производных (матрица Гессе, гессиан).
Если гессиан положительно определен, то локальный минимум этой функции можно найти, приравняв нулевой градиент квадратичной формы к нулю. В результате получится выражение:

Обратный гессиан вычисляется с помощью метода сопряженных градиентов. Пример использования этого метода для минимизации функции Розенброка приведен ниже. Чтобы использовать метод Newton-CG, необходимо задать функцию, которая вычисляет гессиан.
Гессиан функции Розенброка в аналитическом виде равен:

где и , определяют матрицу .

Остальные ненулевые элементы матрицы равны:

Например, в пятимерном пространстве N = 5, матрица Гессе для функции Розенброка имеет ленточный вид:

Код, который вычисляет этот гессиан вместе с кодом для минимизации функции Розенброка с помощью метода сопряженных градиентов (Ньютона):

def rosen_hess(x): x = np.asarray(x) H = np.diag(-400*x[:-1],1) — np.diag(400*x[:-1],-1) diagonal = np.zeros_like(x) diagonal[0] = 1200*x[0]**2-400*x[1]+2 diagonal[-1] = 200 diagonal[1:-1] = 202 + 1200*x[1:-1]**2 — 400*x[2:] H = H + np.diag(diagonal) return H res = minimize(rosen, x0, method=’Newton-CG’, jac=rosen_der, hess=rosen_hess, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 24 Function evaluations: 33 Gradient evaluations: 56 Hessian evaluations: 24 [1. 1. 1. 0.99999999 0.99999999]

Пример с определением функции произведения гессиана и произвольного вектора

В реальных задачах вычисление и хранение всей матрицы Гессе может потребовать значительных ресурсов времени и памяти. При этом фактически нет необходимости задавать саму матрицу Гессе, т.к. для процедуры минимизации нужен только вектор, равный произведению гессиана с другим произвольным вектором. Таким образом, с вычислительной точки зрения намного предпочтительней сразу определить функцию, которая возвращает результат произведения гессиана с произвольным вектором.

Рассмотрим функцию hess, которая принимает вектор минимизации в качестве первого аргумента, а произвольный вектор — как второй аргумент (наряду с другими аргументами минимизируемой функции). В нашем случае вычислить произведение гессиана функции Розенброка с произвольным вектором не очень сложно. Если p — произвольный вектор, то произведение имеет вид:

Функция, вычисляющая произведение гессиана и произвольного вектора, передается как значение аргумента hessp функции minimize:

def rosen_hess_p(x, p): x = np.asarray(x) Hp = np.zeros_like(x) Hp[0] = (1200*x[0]**2 — 400*x[1] + 2)*p[0] — 400*x[0]*p[1] Hp[1:-1] = -400*x[:-2]*p[:-2]+(202+1200*x[1:-1]**2-400*x[2:])*p[1:-1] -400*x[1:-1]*p[2:] Hp[-1] = -400*x[-2]*p[-2] + 200*p[-1] return Hp res = minimize(rosen, x0, method=’Newton-CG’, jac=rosen_der, hessp=rosen_hess_p, options=)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 24 Function evaluations: 33 Gradient evaluations: 56 Hessian evaluations: 66

Алгоритм доверительной области (trust region) сопряженных градиентов (Ньютона)

Плохая обусловленность матрицы Гессе и неверные направления поиска могут привести к тому, что алгоритм сопряженных градиентов Ньютона может быть неэффективным. В таких случаях предпочтение отдается методу доверительной области (trust-region) сопряженных градиентов Ньютона.

Пример с определением матрицы Гессе:

res = minimize(rosen, x0, method=’trust-ncg’, jac=rosen_der, hess=rosen_hess, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 20 Function evaluations: 21 Gradient evaluations: 20 Hessian evaluations: 19 [1. 1. 1. 1. 1.]

Пример с функцией произведения гессиана и произвольного вектора:

res = minimize(rosen, x0, method=’trust-ncg’, jac=rosen_der, hessp=rosen_hess_p, options=) print(res.x)
Optimization terminated successfully. Current function value: 0.000000 Iterations: 20 Function evaluations: 21 Gradient evaluations: 20 Hessian evaluations: 0 [1. 1. 1. 1. 1.]

Методы Крыловского типа

Подобно методу trust-ncg, методы Крыловского типа хорошо подходят для решения крупномасштабных задач, поскольку в них используется только матрично-векторные произведения. Их суть в решении задачи в доверительной области, ограниченной усеченным подпространством Крылова. Для неопределенных задач лучше использовать этот метод, так как он использует меньшее количество нелинейных итераций за счет меньшего количества матрично-векторных произведений на одну подзадачу, по сравнению с методом trust-ncg. Кроме того, решение квадратичной подзадачи находится более точно, чем методом trust-ncg.
Пример с определением матрицы Гессе:

res = minimize(rosen, x0, method=’trust-krylov’, jac=rosen_der, hess=rosen_hess, options=) Optimization terminated successfully. Current function value: 0.000000 Iterations: 19 Function evaluations: 20 Gradient evaluations: 20 Hessian evaluations: 18 print(res.x) [1. 1. 1. 1. 1.]

Пример с функцией произведения гессиана и произвольного вектора:

res = minimize(rosen, x0, method=’trust-krylov’, jac=rosen_der, hessp=rosen_hess_p, options=) Optimization terminated successfully. Current function value: 0.000000 Iterations: 19 Function evaluations: 20 Gradient evaluations: 20 Hessian evaluations: 0 print(res.x) [1. 1. 1. 1. 1.]

Алгоритм приближенного решения в доверительной области

Все методы (Newton-CG, trust-ncg и trust-krylov) хорошо подходят для решения крупномасштабных задач (с тысячами переменных).

Это связано с тем, что лежащий в их основе алгоритм сопряженных градиентов подразумевает приближенное нахождение обратной матрицы Гессе. Решение находится итеративно, без явного разложения гессиана. Поскольку требуется определить только функцию для произведение гессиана и произвольного вектора, этот алгоритм особенно хорош для работы с разреженными (ленточными диагональными) матрицами. Это обеспечивает низкие затраты памяти и значительную экономию времени.

В задачах среднего размера затраты на хранение и факторизацию гессиана не имеют решающего значения. Это значит, что можно получить решение за меньшее количество итераций, разрешив подзадачи области доверия почти точно. Для этого некоторые нелинейные уравнения решаются итеративно для каждой квадратичной подзадачи.

Такое решение требует обычно 3 или 4 разложения Холецкого матрицы Гессе. В результате метод сходится за меньшее количество итераций и требует меньше вычислений целевой функции, чем другие реализованные методы доверительной области. Этот алгоритм подразумевает только определение полной матрицы Гессе и не поддерживает возможность использовать функцию произведения гессиана и произвольного вектора.

Пример с минимизацией функции Розенброка:

res = minimize(rosen, x0, method=’trust-exact’, jac=rosen_der, hess=rosen_hess, options=) res.x
Optimization terminated successfully. Current function value: 0.000000 Iterations: 13 Function evaluations: 14 Gradient evaluations: 13 Hessian evaluations: 14 array([1., 1., 1., 1., 1.])

На этом, пожалуй, остановимся. В следующей статье постараюсь рассказать самое интересное об условной минимизации, приложении минимизации в решении задач аппроксимации, минимизации функции одной переменной, произвольных минимизаторах и поиске корней системы уравнений с помощью пакета scipy.optimize.

Источник: habr.com

Scipy что это за программа

SciPy представляет собой совокупность математических алгоритмов и функций, построенных как расширение Numpy на Python. Он значительно расширяет возможности интерактивной сессии Python, предоставляя пользователю команды высокого уровня и классы для управления и визуализации данных. Со SciPy интерактивный сеанс Python становится средой обработки данных и системой прототипирования соперничающей с такими системами, как MATLAB, IDL, Octave, R-Lab, and SciLab.

Дополнительным преимуществом базирования SciPy на Python является то, что он также является достаточно мощным языком программирования, используемый при разработке сложных программ и специализированных приложений. Научные приложения, так же получают выгоду от разработки дополнительных модулей в многочисленных нишах программного обеспечения разработчиками по всему миру. Все, начиная от параллельного программирования для веб до подпрограмм и классов баз данных доступны для программиста Python. Все эти возможности доступны в дополнение к математической библиотеке SciPy.

Этот учебник ознакомит начинающего пользователя SciPy с некоторыми из его наиболее важных особенностей. Она предполагает, что пользователь уже установил пакет SciPy. Некоторые общие объекты Python также предполагается, например, могут быть приобретены работая через учебник дистрибутива Python. Для получения дополнительной вводной помощи пользователю направляется к документации Numpy.

Для краткости и удобства, мы часто будем предполагать, что основные пакеты (NumPy, SciPy и Matplotlib) были импортированы как:

>>> import numpy as np
>>> import matplotlib as mpl
>>> import matplotlib.pyplot as plt

Это соглашения о виде импорта являются общими, принятыми после публичного обсуждения. Вы увидите эти условные обозначения, во всем исходном коде и документации NumPy и SciPy. В то время как, очевидно, от вас не требуются, следование этим соглашениям в собственном коде, хотя и настоятельно рекомендуется.

Структура SciPy

SciPy организовано в подпакеты, охватывающих различные научные вычислительные области. Они приведены в следующей таблице:

Подпакет
Описание
Алгоритмы кластеризации
Физические и математические константы
Подпрограммы быстрого преобразования Фурье
Интегрирование и решение обыкновенных дифференциальных уравнений
interpolate
Интерполяционные и сглаживающие сплайны
Ввод и вывод

Линейная алгебра
обработка N-мернох изображений
Мультиплексирование с ортогональным расстояние регрессии
Оптимизация и поиск корневых структур
Обработка сигналов
Разреженные матрицы и связанные с ними процедуры

Пространственные структуры данных и алгоритмы
Специальные функции
Статистические распределения и функции
C/C ++ интеграция

SciPy подпакеты должны быть импортированы отдельно, например:

>>> from scipy import linalg, optimize

Из-за повсеместности, некоторые из функций этих подпакетов также доступны в пространстве имен SciPy, чтобы облегчить их использование в интерактивных сессиях и программах. Кроме того, многие основные функции массивов из NumPy также доступны на верхнем уровне SciPy пакета. Прежде чем взглянуть на суб-пакеты по отдельности, мы сначала посмотрим на некоторые из этих общих функций.

Поиск документации

SciPy и NumPy имеют версии документации в HTML и PDF формате доступные на https://docs.scipy.org/~~pobj, которые охватывают практически все доступные функциональные возможности . Тем не менее, эта документация по-прежнему находится в стадии разработки и некоторые части могут быть неполными или отсутствовать. Поскольку мы являемся добровольной организацией и зависим от сообщества, все ваше участие от обратной связи до совершенствования документации и кода — приветствуется и активно поощряется.

Документация языка Python используются в SciPy для он-лайн документации. Есть два способа читать их и получать помощь. Одним из них является команда help в Python в модуле pydoc. Ввод этой команды без аргументов (т.е. >>>help) запускает интерактивную справочную сессию , которая позволяет осуществлять поиск по ключевым словам и модулям, доступных для всего в Python. Во- вторых, выполнив команду help(obj) с объектом в качестве аргумента отображает подпись этого объекта, и его текст документации.

Метод help из pydoc является сложным, но использует страницы для отображения текста. Иногда это может мешать терминалу если вы работаете в пределах интерактивного сеанса. Numpy/scipy специализированная справочная система также доступна командой numpy.info . Строка подписи и документация для объекта, переданного в помощи команды печатаются на стандартный вывод (или в записываемый объект, переданный в качестве третьего аргумента). Второй аргумент numpy.info определяет максимальную длину строки для печати. Если в качестве аргумента передается модуль, то выводится список функций и классов, определенных в этом модуле. Например:

Источник: san-tit.blogspot.com