Цели: Закрепить основные навыки работы в электронных таблицах.
Развитие логического мышления и познавательного интереса.
Воспитание информационной культуры.
II . Повторение основных принципов решения оптимизационных задач с помощью надстройки электронных таблиц «Поиск решения».
Что такое задачи оптимизации?
В каких случаях задача имеет оптимальное решение?
Какие задачи относятся к задачам оптимизации?
Какие правила (алгоритм) следует соблюдать при решении оптимизационных задач?
Как вызвать в электронных таблицах надстройку Поиск решения?
Как активизировать эту надстройку, если она не установлена?
Что такое целевая функция?
Что показывают ограничения в задачах оптимизации?
Задача оптимизации – поиск оптимального (наилучшего) решения данной задачи при соблюдении некоторых условий.
Задача имеет оптимальное решение, если она удовлетворяет двум требованиям:
Имеет более одного решения, т.е. существуют допустимые решения;
Информатика и ИКТ. Моделирование в электронных таблицах. Решение задач
Имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т.е. наилучшим из допустимых.
При решении задач оптимизации целесообразно руководствоваться следующим алгоритмом:
Разобрать условие задачи,
Построить математическую модель,
Установить поисковые величины,
Установить условия оптимизации,
Решить задачу на компьютере,
Целевая функция (критерий оптимизации)
Показывает, в каком смысле решение должно быть оптимальным , т.е. наилучшим. Возможны три вида целевой функции: максимизация, минимизация, назначение заданного значения
Устанавливают зависимости между переменными. Показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении
III . Закрепление практических навыков решения задач оптимизации.
Задача № 1. ( открыть файл-1 из папки урока)
Бык стоит – 10 т.руб., корова – 5 т.руб., а теленок – 500 руб. Сколько можно купить быков, коров и телят на 100 т.руб., при условии, что надо сформировать стадо из 100 голов скота.
Разместим данные задачи в таблице

Построим математическую модель
В качестве целевой функции возьмем величину SUM, она должна быть SUM=100000 руб.
Ограничения (необходимые условия):
X1 0 X2 0 X3 0
Реализуем математическую модель средствами электронных таблиц

Вызываем надстройку Поиск решения и заполняем соответствующие поля

После команды Выполнить получим результат

Проведем анализ полученного результата, проверим, все ли условия задачи выполняются.
Формулы Excel – все особенности, тонкости и трюки в одном видео! — Функции Excel (2)
Задача №2. ( открыть файл
Фабрика выпускает три вида тканей, причем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м — второго и 60 м — третьего. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на один метр тканей представлен в табл.
Определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.
Цена за 1 м ткани вида I равна 80 у. е., II — 70 у. е., III — 60 у. е.
Затраты ресурсов на производство тканей
Разместим данные задачи в таблице

Построим математическую модель в формулах электронных таблиц.
Затраченные суточные ресурсы
F4=C4*C7+D4*D7+E4*E7 и т. д.
Стоимость суточного выпуска тканей по видам:
Целевая функция — общая стоимость за сутки, вычисляется по формуле G4=C9+D9+E9
и в процессе оптимизации должна получить максимальное значение.
Затраченные ресурсы не должны превышать ресурсы, имеющиеся в наличие
Выпуск ткани должен быть не меньше установленного плана
Кол-во произведенной ткани по видам (C7 и т. д.) исчисляется целыми числами (в метрах).
Вызываем надстройку Поиск решения, заполняем соответствующие поля и выполняем поиск.

Задача №3. ( открыть файл-
Производство продукции осуществляется на 4-х предприятиях, а затем развозится в 5 пунктов потребления. Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Хранение на предприятии единицы продукции обходится в 2 у. е. в день, штраф за недопоставленную продукцию— 3,5 у. е. в день. Стоимость перевозки единицы продукции (в у. е.) с предприятий в пункты потребления приведена в табл.
Необходимо минимизировать суммарные транспортные расходы по перевозке продукции.
Предприятия
Пункты потребления
Проверка сбалансированности модели задачи:
модель является сбалансированной, т. к. суммарный объем производимой продукции в день равен суммарному объему потребности в ней:
235 + 175+185 + 175 = 125 + 160 + 60 + 250+ 175.
Поэтому при решении этой задачи не учитываются издержки, связанные со складированием и недопоставкой продукции.
Разместим данные в таблице

Построим математическую модель в формулах электронных таблиц.
Поставки предприятий (для предприятия 1) H4 = СУММ(C4:G4) и т.д.
Поставки по пунктам реализации (для пункта 1) C8 = СУММ(C4:C7) и т.д.
Транспортные расходы на поставку по пунктам реализации
(для пункта 1) С9 = С4*С14+С5*С15+С6*С16+С7*С17 и т.д.
Общие транспортные расходы H9 = СУММ(С9:G9)
Целевая функция — Общие транспортные расходы (ячейка H9 ) должна быть минимальной.
Поставки предприятий должны быть равны их объему производства
Поставки по пунктам реализации должны быть равны их потребности в продукции
Объёмы перевозок не должны быть отрицательными числами
Объёмы перевозок должны быть целыми величинами.
Вызываем надстройку Поиск решения, заполняем соответствующие поля.


В данной задаче, не смотря на большое кол-во взаимосвязанных данных, критерий оптимизации и ограничения являются линейными функциями. В этом случае для решения задачи следует установить флажок Линейная модель в окне Параметры поиска решения . Это обеспечит применение симплекс-метода, в противном случае будут использоваться более общие методы, что может привести к неверному результату.
IV . Подведение итогов урока.
Для чего предназначена надстройка электронных таблиц Поиск решения?
Каковы основные этапы при решении оптимизационных задач?
В каких сферах деятельности человека встречаются оптимизационные задачи?
V. Домашнее задание.
Сформулировать задачу оптимизации и решить ее средствами электронных таблиц.
Источник: xn--j1ahfl.xn--p1ai
Решение задач в электронных таблицах Excel. Цели работы Я показала в данной работе, как с помощью электронных таблиц эффективно решать задачи из разных. — презентация
Презентация на тему: » Решение задач в электронных таблицах Excel. Цели работы Я показала в данной работе, как с помощью электронных таблиц эффективно решать задачи из разных.» — Транскрипт:
1 Решение задач в электронных таблицах Excel
2 Цели работы Я показала в данной работе, как с помощью электронных таблиц эффективно решать задачи из разных сфер жизни: Решение задач по физике(аналогично можно решить задачи по химии, математике и т. д)физике( Решение статистической задачистатистической задачи Решение задачи по результатам исследованийисследований Составление интерактивного тестаинтерактивного теста Решение задачи моделирования жизненной ситуациижизненной ситуации
3 Введение Огромные возможности для моделирования несет в себе среда электронной таблицы. Это объясняется тем, что она: 1. одна из самых распространенных программных сред общего назначения и владение технологий работы в ней является одним из показателей информационной культуры человека. 2. позволяет обрабатывать большие массивы числовых данных, например статистические данные, результаты экспериментов и многое другое. 3. позволяет достаточно просто решить большое разнообразие задач (Самое главное-это связать параметры, описывающие объект, явление или процесс, некоторыми математическими соотношениями). 4. позволяет получить результаты моделирования практически мгновенно, с использованием простых технологий
4 Достоинства электронных таблиц Меня привлекло это задание тем, что в нем нужно показать решение множества задач из различных сфер в электронных таблицах. Поставленные задачи обычно решают с помощью языков программирования или другими средствами, хотя эти задачи можно легко и эффективно решать средствами Excel.
5 Этапы решения задач(эл. табл.) 1. Постановка задачи(выяснение условий, оформление решения разделов «дано» и «найти», заполнение таблицы данными, которые содержит в себе задача). 2. Составление математической модели.математической модели 3. Составление алгоритма решения. 4. Оформление решения формул в виде текста в разделе «математическая модель». 5. Создание сетки вычислений в разделе «решение». 6. Анализ полученных результатов.
6 Пример: Шарик плотностью 0.8 г/см 3, радиусом 5 см бросили вверх с начальной скоростью 25 м/с, какова максимальная высота подъема шарика, и какой энергией он будет при этом обладать? Постановка задачи Составление математической модели Составление алгоритма решения
7 Пример: Создание сетки вычислений в разделе «решение» Анализ полученных результатов
8 Ввод формул. Задачи
9 Пример: Благодаря Excel мы можем исследовать разного рода зависимости, в данном случае проанализировать и построить функцию Ep(V), Как видно это самый универсальный способ просчитывания и составления таблиц, простым перемещением курсора была составлена таблица в 50 строк. назад
10 Представление о математической модели Модель-это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Часто исследуемый объект или процесс может быть описан в виде формул, связывающих его количественные параметры(т.е. математическая модель-это описание объекта или процесса математическими формулами, связывающими их количественные параметры). Для описания математических моделей используется различные системы обозначений, принятые в той или иной науке. Составление математической модели заключается в выводе математических формул, связывающих ее параметры, по которым в дальнейшем будет производиться расчет. Компьютер позволяет на качественно новом уровне перевести мысленную модель в знаковую формулу. назад
Источник: www.myshared.ru
Решение задач в электронных таблицах программа
Внимание Скидка 50% на курсы! Спешите подать
заявку
Профессиональной переподготовки 30 курсов от 6900 руб.
Курсы для всех от 3000 руб. от 1500 руб.
Повышение квалификации 36 курсов от 1500 руб.
Лицензия №037267 от 17.03.2016 г.
выдана департаментом образования г. Москвы

Практическая работа по Информатике «Решение задач с применением редактора электронных таблиц MS Excel»
Государственное автономное профессиональное образовательное учреждение Саратовской области
«Энгельсский колледж профессиональных технологий»
«Решение задач с применением редактора электронных таблиц MS Excel »
Составитель: преподаватель информатики
Жданова Анна Александровна
Практическая работа по дисциплине «Информатика и ИКТ» специальности «Техническое обслуживание и ремонт автомобильного транспорта» 1 курс
Тема: «Решение задач с применением редактора электронных таблиц MS Excel »
Тип урока: урок систематизации и обобщения знаний и умений.
Цель работы: закрепить теоретические знания по теме; получить навыки работы со статистическими функциями, изучить синтаксис некоторых функций, научиться решать задачи на поиск решения и подбор параметра, осуществлять анализ данных средствами редактора электронных таблиц.
Практическая работа заключается в решении экономических задач анализа данных. Представлена технология выполнения типовых задач с подробным описанием последовательности действий в редакторе электронных таблиц MS Excel . Для успешного выполнения задания необходимо повторить теоретические знания по темам: Обзор программного обеспечения для работы с электронными документами.
Текстовые, табличные процессоры. Обзор программного обеспечения для обработки на ПК числовых данных. Применение определенного класса программ при решении конкретных задач. Статистические функции программы Microsoft Excel . Методы анализа доходов и прибыли, фиксированных активов, инвестиций.
2. Краткая теоретическая справка по использованию статистических функций.
Статистическая функция вставляется через меню Формулы→Вставить функцию
. Появится окно Мастер функций.
В окне Мастера функций выберите категорию Статистические, а затем конкретную функцию:
.
Клавиша F 1вызовет справку по функции.
Для каждой функции имеются свои аргументы. Например, для функции СРЗНАЧМН:
Диапазон усреднения; Диапазон условия 1; условие 1;Диапазон условия 2; условие 2 и т.д.
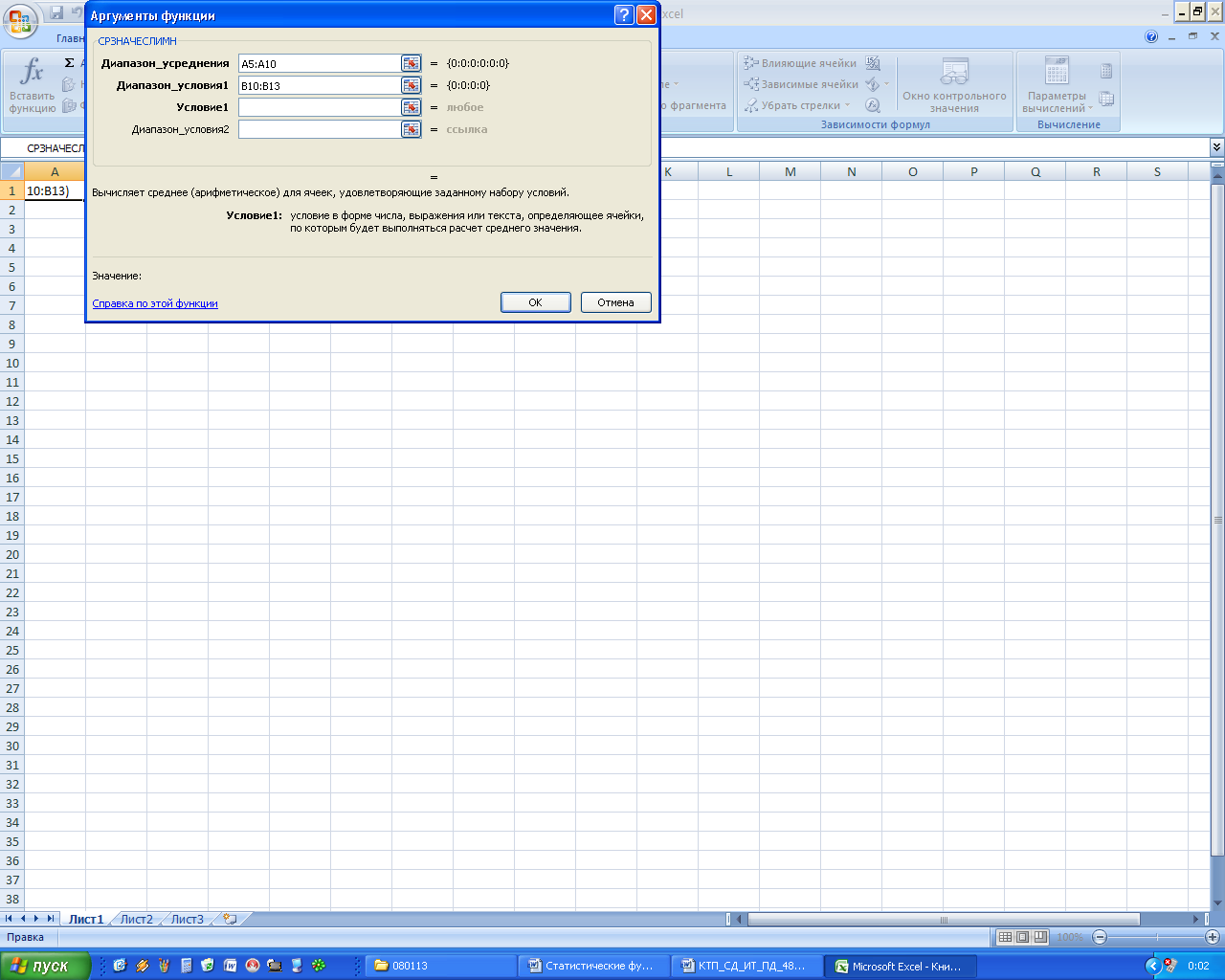
Примеры использования статистических функций:
Заведующему отделом продаж может понадобиться спланировать продажи на следующий квартал (функция ТЕНДЕНЦИЯ).
Учителю может понадобиться построить кривую на базе средних оценок (СРЗНАЧ или МЕДИАНА, может быть даже МОДА).
Производитель, проверяющий качество продукта, может быть заинтересован в том, чтобы производимые изделия попадали в диапазон приемлемого качества (СТАНДОТКЛОН или ДИСП).
Исследователю рынка может потребоваться узнать, сколько ответов на опрос попадает в заданный диапазон (ЧАСТОТА).
Заведующая отделом продаж использует функцию ДИСП для анализа показателей продаж трех продавцов.
3. Краткая теоретическая справка по использования пакета анализа данных.
Пакет анализа . В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде. Доступные средства: Чтобы просмотреть список доступных инструментов анализа, выберите команду Анализ данных в меню Сервис . Если команда Анализ данных в меню Сервис отсутствует — необходима установка пакета анализа.
Для успешного применения процедур анализа необходимы начальные знания в области статистических и инженерных расчетов, для которых эти инструменты были разработаны.
Подбор параметра . При обработке табличных данных часто возникает необходимость в прогнозировании результата на основе известных исходных значений или, наоборот, в определении того, какими должны быть исходные значения, позволяющие получить нужный результат. Подбор параметра осуществляется с помощью команды Данные→Анализ «что-если»→ Подбор параметра
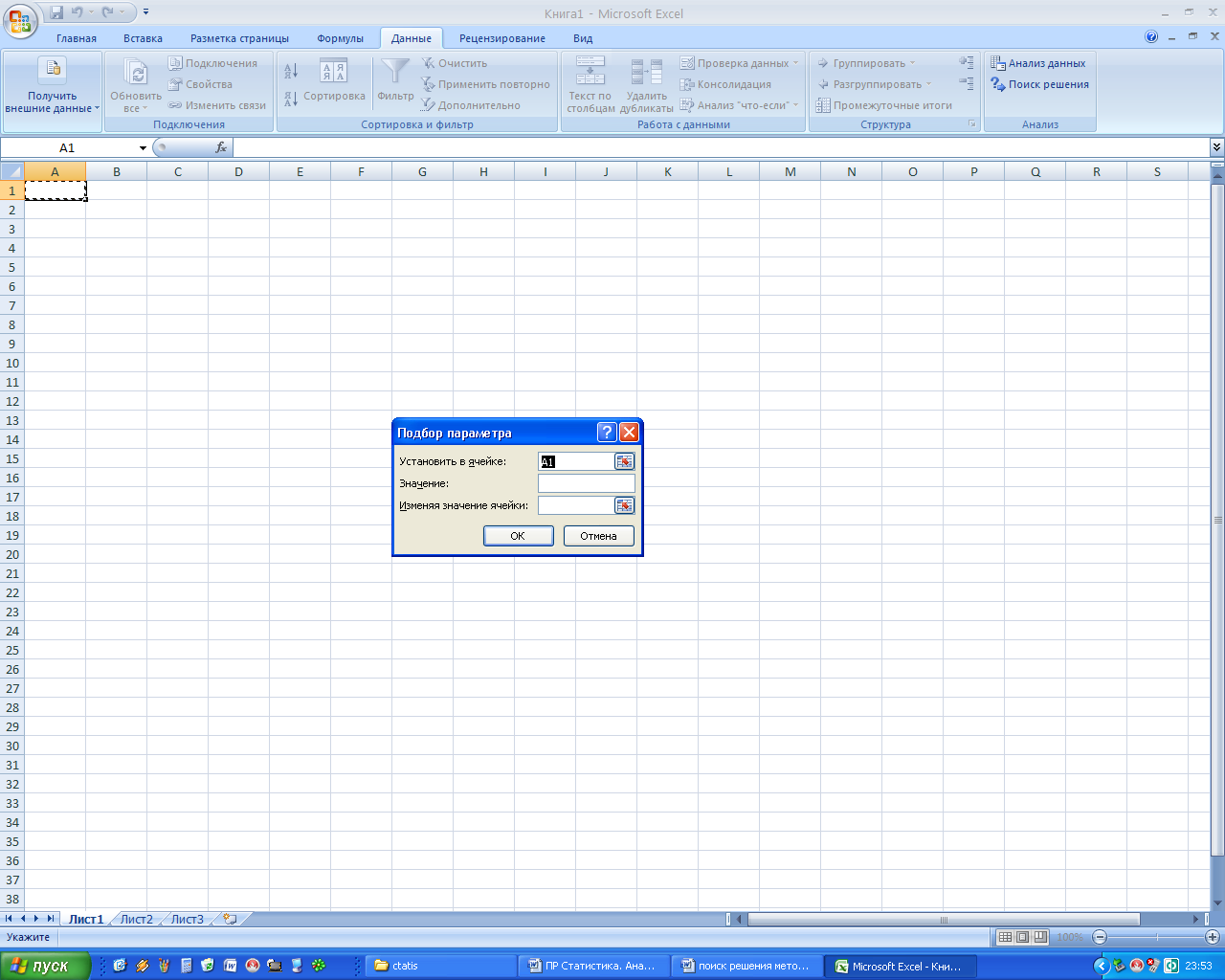
В поле Установить в ячейке появившегося диалогового окна будет отображаться адрес целевой ячейки. Задайте в поле Значение значение, которое должна содержать целевая ячейка. Укажите в поле Изменяя значение ячейки адрес ячейки, значение которой необходимо установить таким, чтобы в целевой ячейке получить заданное значение. Нажмите кнопку ОК , и нужный параметр будет подобран. Инструмент Подбор параметра помогает решить задачу, когда известно, что должно получиться в ответе, но не известно, какое значение должна иметь одна из переменных.
Поиск решения. Окно средства:
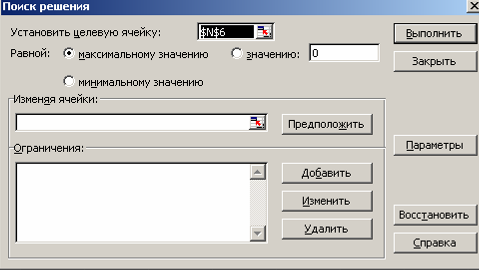
Перед запуском процедуры поиска решения исходные данные должны быть представлены в виде таблицы, которая содержит формулы, отражающие зависимости между данными таблицы.
С помощью команды Поиск решения можно оптимизировать модель сбыта или график занятости, решить любую транспортную задачу или задачу, связанную с управлением производством и денежными средствами.
Для того чтобы запустить процедуру поиска решения, необходимо выделить целевую ячейку и вызвать команду Данные Поиск решения . В поле Установить целевую ячейку данного окна указывается адрес целевой ячейки. Переключатели Равной задают ее значение — максимальному значению, минимальному значению или значению. В последнем случае значение вводится в поле справа. В поле Изменяя ячейки указывается, в каких ячейках программа должна изменить значения для получения оптимального результата.
При нажатии кнопки Предположить программа выделяет диапазон ячеек, на которые имеется ссылка в целевой ячейке. Заданные ограничения перечислены в списке Ограничения. При необходимости ввести дополнительное ограничение нужно посредством щелчка на кнопке Добавить .
В поле Ссыпка на ячейку этого окна введите адрес ячейки, содержимое которой должно удовлетворять заданному ограничению, а в поле Ограничение укажите значение, выступающее в качестве ограничения, или адрес ячейки с таким значением. Между этими двумя полями находится еще одно, в котором устанавливается оператор, определяющий отношение между значением ячейки и ограничением. После нажатия кнопки заданное ограничение появится в диалоговом окне Поиск решения .
Найденное решение можно сохранить в виде файла. Для этого нажмите кнопку Сохранить сценарий и в открывшемся окне задайте имя файла.
4. СОДЕРЖАНИЕ РАБОТЫ
Упражнение 1. ВЫЧИСЛЕНИЕ ДИСПЕРСИИ . Представьте себе заведующего отделом продаж, изучающего показатели продаж трех различных продавцов, чтобы сравнить их производительность. Одна из множества статистических функций, доступных заведующему – вычисление дисперсии (ДИСП).
Дисперсия позволяет измерить, насколько данные отличаются друг от друга. Данные с низкой дисперсией состоят из идентичных или близких значений: 6, 7, 6, 6, 7. Данные с высокой дисперсией содержат сильно отличающиеся значения: 598, 1, 134, 5, 92.
Вычислить дисперсию сотрудников фирмы Батурина, Королева, Рощина. Объяснить полученные результаты вычислений в ячейках. Найти интервалы продаж каждого сотрудника (т.е. минимальное и максимальное значения)
- Какие статистические функции использовались в практической работе?
- Как создать статистическую формулу?
- Назовите аргументы функции СЧЕТЕСЛИМН.
- В чем смысл инструмента Подбор параметра?
- Чем является целевая ячейка в надстройке Поиск решения?
Источник: doc4web.ru