
Решение задач линейного программирования симплекс-методом Калькулятор онлайн

Как онлайн калькулятор находит решение задачи линейного программирования? Он выдаёт шаги решения задачи симплекс методом, на которых преобразуется система ограничений и целевая функция. Это значит, что на соответствующем шаге функция цели не принимает оптимального значения и по определённому правилу совершается переход от одной вершины многогранника решений к другой пока функция цели не примет оптимального значения. По шагам решения можно наблюдать, как переменные, которые входят в выражение целевой функции с коэффициентом 0, являются неосновными, а остальные — основными. Таким образом осуществляется перевод переменных в основные и неосновные.
Материалы по теме Линейное программирование
Поделиться с друзьями



Графический метод решения задач линейного программирования | Высшая математика TutorOnline
Симплексный метод является универсальным методом решения оптимизационных задач. За исходное решение берётся одно из возможных базисных решений (или «план», «программа»). Затем эта программа улучшается до тех пор, пока не будет найдена оптимальная программа. Наш калькулятор онлайн позволяет решать задачи как на максимум целевой функции, так и на минимум.
При решении задач на минимум исходная задача линейного программирования сводится к двойственной задаче. При выполнении этих операций на бумаге часто возникают ошибки, а наш калькулятор онлайн поможет своевременно проверить ошибки. Вычисление происходит за время немногим более секунды. Этот калькулятор находит максимум целевой функции. Если требуется найти минимум целевой функции, то следует воспользоваться калькулятором Решение двойственной задачи линейного программирования.
Источник: function-x.ru
Симплекс-метод решения задачи линейного программирования в Excel
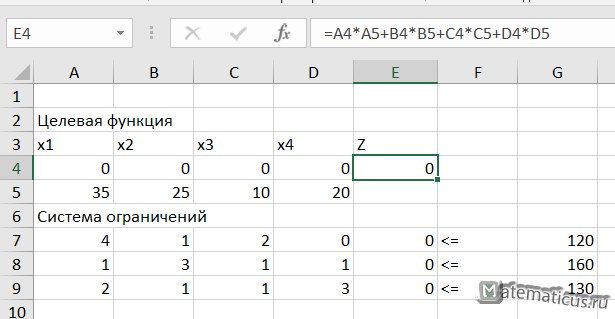
Теперь данную задачу для решения запишем в Excel

В ячейке E4 вставим формулу
=A4*A5+B4*B5+C4*C5+D4*D5
Для ячейки E7, E8 и E9 формула будет иметь вид
=$A$4*A7+$B$4*B7+$C$4*C7+$D$4*D7
=$A$4*A8+$B$4*B8+$C$4*C8+$D$4*D8
=$A$4*A9+$B$4*B9+$C$4*C9+$D$4*D9
Также можно воспользоваться формулой:
=СУММПРОИЗВ(A4:D4;A7:D7)
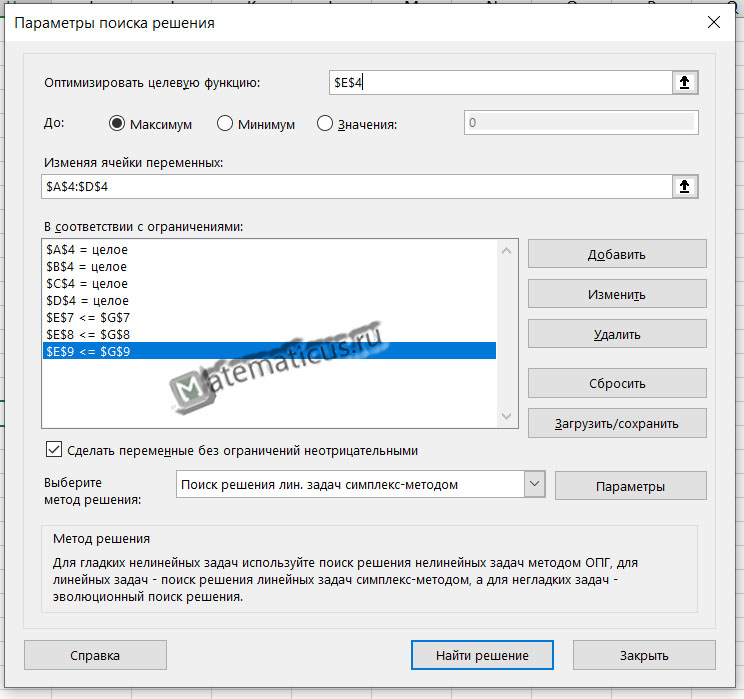
На вкладке данные переходим в Поиск решения
Выбираем ячейку с целевой функцией, ставим галочку максимум, далее выбираем ячейки изменяемых переменных ($A$4:$D$4) и добавляем ограничения при помощи кнопки Добавить. Также ставим галочку переменные без ограничений неотрицательные, выбираем, выбираем метод решения – симплекс-метод решения линейных задач.
Cимплексный метод решения задачи линейного программирования (ЗЛП)
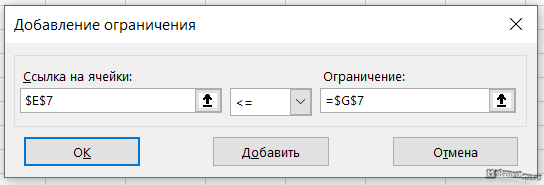
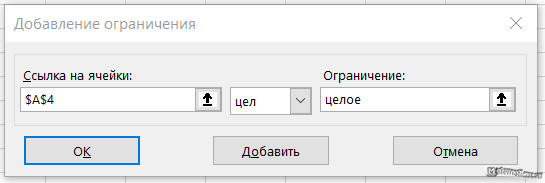
Можно также перейти в параметры и настроить точность.
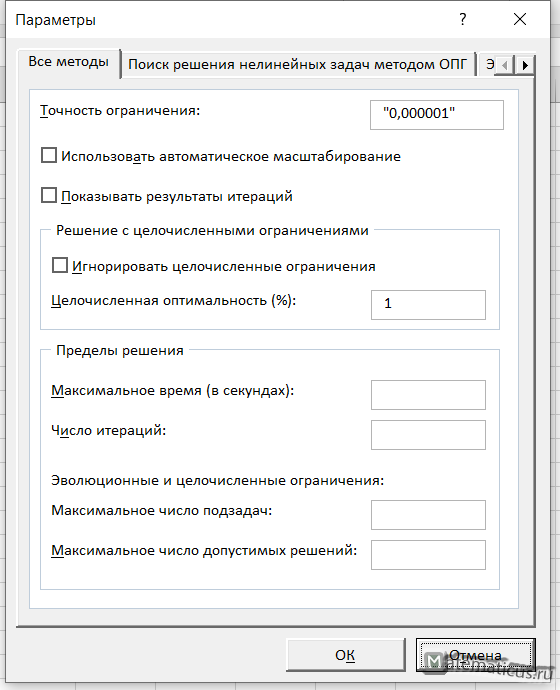
Итак, нажимаем Найти решение, появляется окно результаты поиска решений, выбираем сохранить найденное решение.
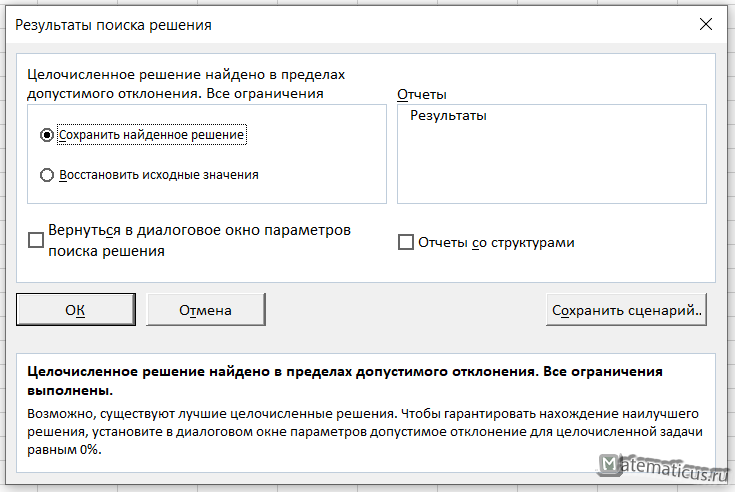
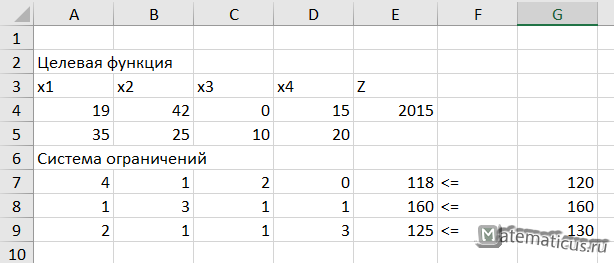
В итоги получили решения задачи
Z=2015
x1=19; x2=42; x3=0; x4=15

24345
Источник: www.matematicus.ru