3 2. Подбор параметра Когда желаемый результат вычислений по формуле известен , но неизвестны значения , необходимые для получения этого результата , можно воспользоваться средством Подбор параметра , выбрав команду Подбор параметра в меню Сервис . При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор , пока вычисления по формуле , ссылающейся на эту ячейку , не дадут нужного результата . Возьмем в качестве примера все то же квадратное уравнение х 2 -5 х +6=0 . Для нахождения корней уравнения выполним следующие действия : Рис . 2. Окно диалога Подбор параметра ∙ В ячейку С 3 ( рис . 2) введем формулу для вычисления значения функции , стоящей в уравнении слева от знака равенства . В качестве аргумента используем ссылку на ячейку С 2, т . е . =С2^2-5*C2+6 . ∙ В окне диалога Подбор параметра ( рис . 2) в поле Установить в ячейке введем ссылку на ячейку с формулой , в поле Значение — ожидаемый результат , в поле Изменяя значения ячейки — ссылку на ячейку , в которой будет храниться значение подбираемого параметра ( содержимое этой ячейки не может быть формулой ). ∙ После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра . Если подобранное значение необходимо сохранить , то нажмите на О k , и результат будет сохранен в ячейке , заданной ранее в поле Изменяя значения ячейки . Для восстановления значения , которое было в ячейке С 2 до использования команды Подбор параметра , нажмите кнопку Отмена .
Как найти корни уравнения в Excel с помощью Подбора параметра
4 3. Поиск решения Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения , зависящего от одного неизвестного параметра . Для более сложных задач следует использовать команду Поиск решения ( Решатель ), доступ к которой реализован через пункт меню Сервис / Поиск решения . Рассмотрим , как воспользоваться Поиском решения на примере того же квадратного уравнения . Рис . 3. Окно диалога Поиск решения После открытия диалога Поиск решения ( рис . 3) необходимо выполнить следующие действия : 1) в поле Установить целевую ячейку ввести адрес ячейки , содержащей формулу для вычисления значений оптимизируемой функции , в нашем примере целевая ячейка — это С 4, а формула в ней имеет вид : = C3^2 — 5*C3 + 6 ; 2) для ввода значения целевой ячейки , установить переключатель значению в положение 0; 3) в поле Изменяя ячейки ввести адреса изменяемых ячеек , т . е . аргументов целевой функции ($ С $3) ( или щелкая мышью при нажатой клавише С trl на соответствующих ячейках ), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить ;
5 4) в поле Ограничения с помощью кнопки Добавить ввести все ограничения , которым должен отвечать результат поиска : для нашего примера ограничений задавать не нужно ; 5) для запуска процесса поиска решения нажать кнопку Выполнить . Рис . 4. Результаты поиска Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения . После чего рабочий лист примет вид , представленный на рис . 4. Полученное решение зависит от выбора начального приближения , которое задается в ячейке С 4 ( аргумент функции ). Если в качестве начального приближения в ячейку С 4 ввести значение , равное 1,0 , то с помощью Поиска решения найдем второй корень , равный 2,0 .
6 4. Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений рассмотрим на примере системы трёх линейных уравнений
| ì | x + 3y + 5z = 4 | ||||
| ï | 7 x + 8 y + 9z = 2 | ||||
| í | |||||
| ï | |||||
| î 2x + 5 y + 6 z = — 3 | |||||
| 1 | 3 | 5 | |||
| Тогда главный определитель будет равен = | 7 | 8 | 9 | = 26 | |
| 2 | 5 | 6 | |||
| Дополнительные определители : | ||||||||||||||
| 4 | 3 | 5 | 1 | 4 | 5 | 1 | 3 | 4 | ||||||
| x = | 2 | 8 | 9 | = 65 , | y = | 7 | 2 | 9 | = — 182 , | z = | 7 | 8 | 2 | = 117 . |
| — 3 5 | 6 | 2 | — 3 6 | 2 | 5 | — 3 | ||||||||
Решения системы уравнений будет определяться следующими соотношениями : x = x = 2,5 ; y = y = — 7 ; z = z = 4,5 . Для решения системы линейных уравнений в табличном процессоре MS Excel запишем главный определитель в ячейки A2:C4, дополнительные – x в ячейки A6:C8, y – A10:C12, z – A14:C16. Тогда определители можно найти с помощью функции МОПРЕД : F2 = МОПРЕД (A2:C4); F3= МОПРЕД (A6:C8); F4= МОПРЕД (A10:C12) F5= МОПРЕД (A14:C12) Решение системы уравнений будет равно : x =F3/F2; y =F4/F2; z =F5/F2.
7 5. Решение систем линейных матричным способом Воспользуемся предыдущей системой линейных уравнений : ì x + 3y + 5z = 4 ï í 7 x + 8 y + 9z = 2 ï î 2x + 5 y + 6 z = — 3 Данную систему линейных уравнений можно записать в матричной форме :
| æ 1 | 3 5 | ö | æ x ö | æ | 4 ö | |||||
| ç | 7 | 8 | 9 | ÷ | , | ç | ÷ | ç | 5 | ÷ |
| A × X = B , где A = ç | ÷ | X = ç y ÷ | , B = ç | ÷ . | ||||||
| ç | 2 | 5 | 6 | ÷ | ç | ÷ | ç | — 3 | ÷ | |
| è | ø | è z ø | è | ø | ||||||
Решение будем искать из уравнения вида : X = A − 1 × B , где A − 1 – обратная матрица матрице A . Для системы в Excel запишем коэффициентов при неизвестных в ячейках B2:D4, матрицу столбец – F2:F4 ( рис . 5). Рис . 5 Тогда с помощью функции = МОБР (B2:D4) можно найти обратную матрицу A − 1 , для чего : 1. В ячейке B6 введите функцию МОБР (B2:D4). 2. Выделите диапазон ячеек B6:D8. 3. Нажмите клавишу F2 . 4. Нажмите комбинацию клавиш Shift+Ctrl+Enter . Для нахождения решения системы уравнений надо перемножить матрицу A − 1 на матрицу — столбец B . Для этого : 1. В ячейке F6 введите функцию = МУМНОЖ (B6:D8;F2:F4). 2. Выделите диапазон ячеек F6:F8. 3. Нажмите клавишу F2 . 4. Нажмите комбинацию клавиш Shift+Ctrl+Enter .
8 6. Варианты заданий
| № | f ( x ) | № | f ( x ) | ||||||||||||
| варианта | варианта | ||||||||||||||
| 1 | e x − 1 — x 3 — x | 9 | 0.25x 3 + x — 2 | ||||||||||||
| x Î [0,1] | x Î [0, 2 ] | ||||||||||||||
| 1 | 1 − x 2 | ||||||||||||||
| x — | arccos | − x | |||||||||||||
| 2 | 3 + sin( 3.6 x ) | 10 | 1 + x 2 | ||||||||||||
| x Î [0,1] | x [ 2,3 ] | ||||||||||||||
| 3x − 4ln x − 5 | |||||||||||||||
| 3 | arccos x — | 1 — 0.3x 3 | 11 | ||||||||||||
| x Î [0,1] | x Î [ 2, 4 ] | ||||||||||||||
| e x | — e − x — 2 | ||||||||||||||
| 4 | 1 — 0.4x 2 — arcsin x | 12 | |||||||||||||
| x Î [0,1] | x Î [0,1] | ||||||||||||||
| 3x — 14 + e x — e − x | — tg x | ||||||||||||||
| 5 | 13 | 1 — x | |||||||||||||
| x Î [1,3] | x Î [0,1] | ||||||||||||||
| 1 − x + sin x − ln(1 + x ) | |||||||||||||||
| 6 | 2x 2 | + 1,2 — cos x — 1 | 14 | ||||||||||||
| x Î [0,1] | x Î [0, 2] | ||||||||||||||
| æ 2 | ö | æ 1 | ö | + | 1 | x 5 | — x — 0,2 | ||||||||
| 7 | cos ç | ÷ — 2 sin ç | ÷ | x | 15 | ||||||||||
| è x | ø | è x | ø | x Î [1, 2] | |||||||||||
| x Î [1, 2] | |||||||||||||||
| 8 | 0.1x 2 — x ln x | 16 | x + 0,5 = e − x 2 | ||||||||||||
| x | Î [1, 2 ] | x Î [0,1] | |||||||||||||
| 9 | ||||||||||||||||
| 7. Решить систему уравнений. | ||||||||||||||||
| ì 2x 1 — x 2 — x 3 = 4 | ì x 1 + 4x 2 − x 3 = 2 | |||||||||||||||
| 1. | ï | + 4x 2 | — 2x 3 = — 1 | 2. | ï | + 2x 2 + 2x 3 = 1 | ||||||||||
| í 3x 1 | í 3x 1 | |||||||||||||||
| ï | 3x 1 | — 2x 2 | + 4x 3 = 11 | ï | + 4x 2 — 2x 3 = 5 | |||||||||||
| î | î 6x 1 | |||||||||||||||
| ì x 1 + 3x 2 + 2x 3 − 4 = 0 | ì x 1 − x 2 + 2x 3 = 11 | |||||||||||||||
| 3. | ï | + 6x 2 + x 3 — 2 = 0 | 4. | ï | + 2x 2 — x 3 = 11 | |||||||||||
| í 2x 1 | í x 1 | |||||||||||||||
| ï | + 8x 2 — x 3 — 2 = 0 | ï | — 3x 2 — 3x 3 = 24 | |||||||||||||
| î 4x 1 | î 4x 1 | |||||||||||||||
| ì x 1 + 2x 2 + 4x 3 = 31 | ì x 1 + x 2 + 2x 3 = −1 | |||||||||||||||
| 5. | ï | + x 2 + 2x 3 = 29 | 6. | ï | — x 2 + 2x 3 = — 4 | |||||||||||
| í 5x 1 | í 2x 1 | |||||||||||||||
| ï | — x 2 + x 3 = 10 | ï | + x 2 + 4x 3 = — 2 | |||||||||||||
| î 3x 1 | î 4x 1 | |||||||||||||||
| ì x 1 − 3x 2 − 4x 3 = 4 | ì x 1 + 2x 2 + 3x 3 = 2 | |||||||||||||||
| 7. | ï | + x 2 — 3x 3 = — 1 | 8. | ï | + x 2 + 2x 3 = 3 | |||||||||||
| í 2x 1 | í 3x 1 | |||||||||||||||
| ï | — 2x 2 | + x 3 = 11 | ï | + 3x 2 + x 3 = 1 | ||||||||||||
| î 3x 1 | î 2x 1 | |||||||||||||||
| ì 3x 1 + 2x 2 + 4x 3 = 6 | ì x 1 + 2x 2 + 3x 3 = 5 | |||||||||||||||
| 9. | ï | 4x 1 | — 3x 2 | — 8x 3 | = 6 | 10. | ï | + x 2 + 2x 3 | = 6 | |||||||
| í | í 3x 1 | |||||||||||||||
| ï | + 10x 2 | + 8x 3 | = — 8 | ï | = 1 | |||||||||||
| î 2x 1 | î 2x 1 + 3x 2 + x 3 | |||||||||||||||
| ì- x 1 + 3x 2 + 2x 3 = 6 | ì 2x 1 — x 2 + x 3 = 2 | |||||||||||||||
| ï | 2x 1 + 8x 2 + x 3 = 3 | 12. | ï | + 2x 2 + 2x 3 | = — 2 | |||||||||||
| 11. í | í 3x 1 | |||||||||||||||
| ï | x 1 | + x 2 | + 2x 3 = 6 | ï | 2x 2 + 7x 3 = 17 | |||||||||||
| î | î | |||||||||||||||
| ì | 2x 1 — x 2 = — 1 | ì x 1 − x 2 + 2x 3 = 11 | ||||||||||||||
| 13. | ï | + x 2 | + 2x 3 = 6 | 14. | ï | = 11 | ||||||||||
| í 3x 1 | í x 1 + 2x 2 — x 3 | |||||||||||||||
| ï | + 3x 2 + x 3 = 1 | ï 4x | — 3x | — 3x | = 24 | |||||||||||
| î 2x 1 | 2 | 3 | ||||||||||||||
| î | 1 | |||||||||||||||
| ì x 1 − 3x 2 − 4x 3 = 4 | ì 3x 1 + 2x 2 + 4x 3 = 6 | |||||||||||||||
| 15. | ï | + x 2 | — 3x 3 = — 1 | 16. | ï | = 6 | ||||||||||
| í 2x 1 | í 4x 1 — 3x 2 — 8x 3 | |||||||||||||||
| ï | 3x 1 | — 2x 2 + x 3 | = 11 | ï | = — 8 | |||||||||||
| î | î 2x 1 + 10x 2 + 8x 3 | |||||||||||||||
| ì 2x 1 − x | 2 − x 3 = 4 | ì x 1 + 4x 2 − x 3 = 2 | ||||||||||||||
| 17. | ï | + 4x 2 — 2x 3 = 11 | 18. | ï | ||||||||||||
| í 3x 1 | í 3x 1 + 2x 2 + 2x 3 = 1 | |||||||||||||||
| ï | — 2x 2 + 4x 3 = 11 | ï | ||||||||||||||
| î 3x 1 | î 6x 1 + 4x 2 — 2x 3 = 5 | |||||||||||||||
| ì x 1 + 2x 2 + 4x 3 = 31 | ì x 1 + 2x 2 + 3x 3 = 2 | |||||||||||||||
| 19. | ï | + x 2 + 2x 3 = 29 | 20. | ï | = 3 | |||||||||||
| í 5x 1 | í 3x 1 + x 2 + 2x 3 | |||||||||||||||
| ï | 3x 1 — x 2 | + x 3 = 10 | ï | |||||||||||||
| î | î 2x 1 + 3x 2 + x 3 = 1 | |||||||||||||||
| 10 | |||||||
| ì x 1 + 2x 2 + 3x 3 = 5 | ì x 1 + 3x 2 + 2x 3 − 4 = 0 | ||||||
| 21. | ï | + x 2 + 2x 3 | = 6 | 22. | ï | + 6x 2 | + x 3 — 2 = 0 |
| í 3x 1 | í 2x 1 | ||||||
| ï | + 3x 2 + x 3 | = 1 | ï | + 8x 2 | — x 3 — 2 = 0 | ||
| î 2x 1 | î 4x 1 | ||||||
ì x 1 + x 2 + 2x 3 = −1 23. ï í 2x 1 — x 2 + 2x 3 = — 4 ï î 4x 1 + x 2 + 4x 3 = — 2
Источник: studfile.net
Решение системы уравнений в Excel
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности. В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача: Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч? Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 🙂 Но весьма скоро, я уверен, вы сообразите, что на самом деле всё не так примитивно и для получения ответа нужно решить простую систему уравнений (здесь b — это бита, а m — это мяч):
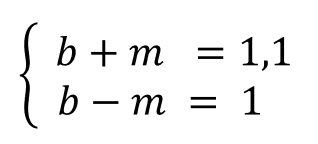
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
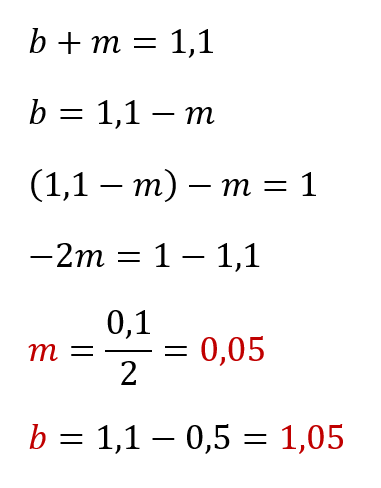
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
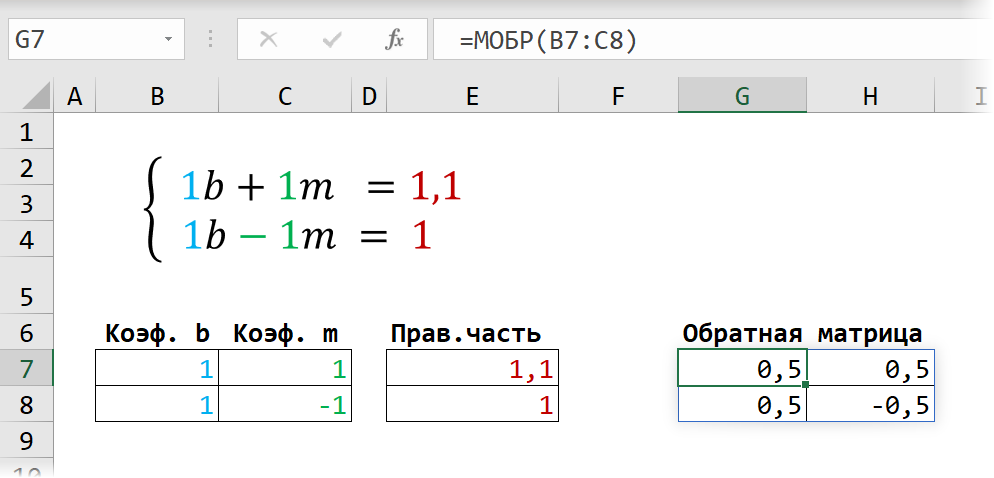
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера. Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше). Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE) :
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl + Shift + Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT) :
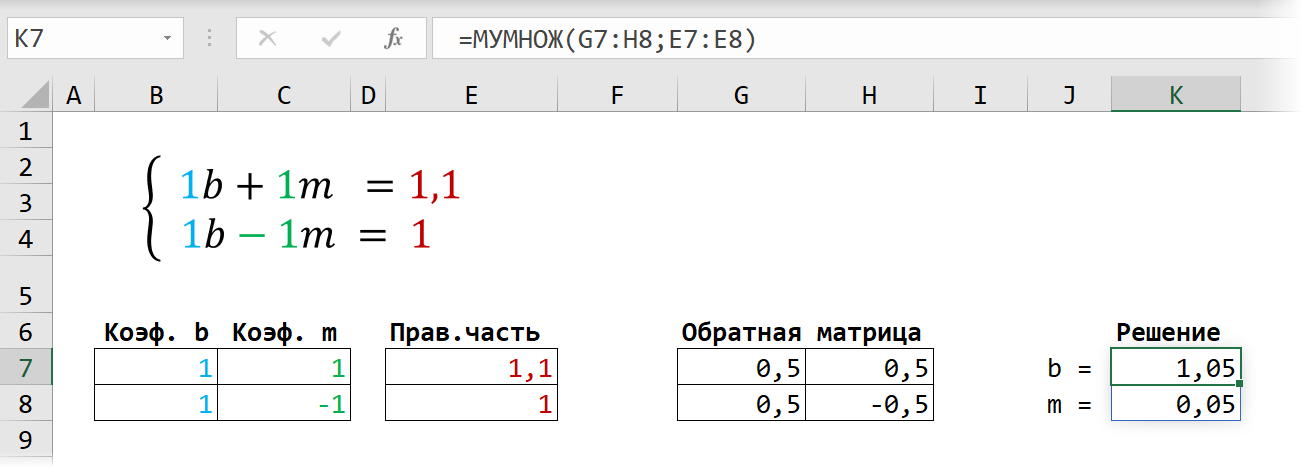
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl + Shift + Enter .
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
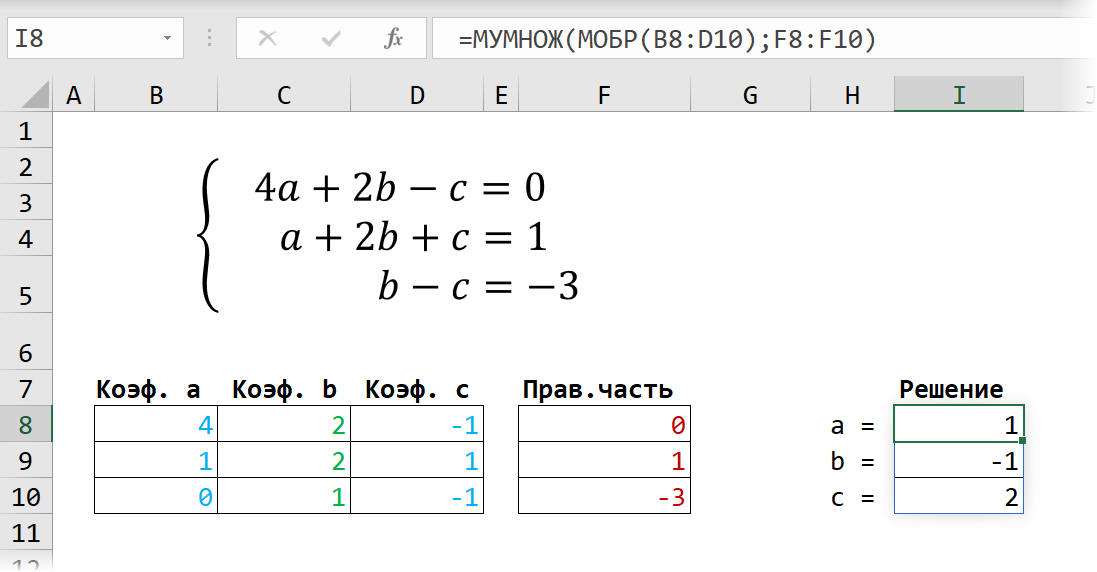
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver) . Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins) .
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
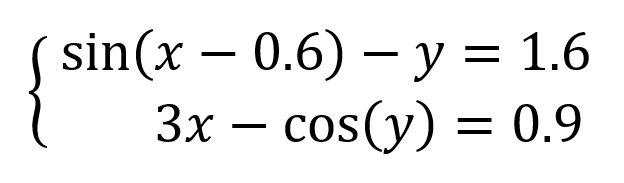
Подготавливаем основу для оптимизации в Excel:

- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column) .
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
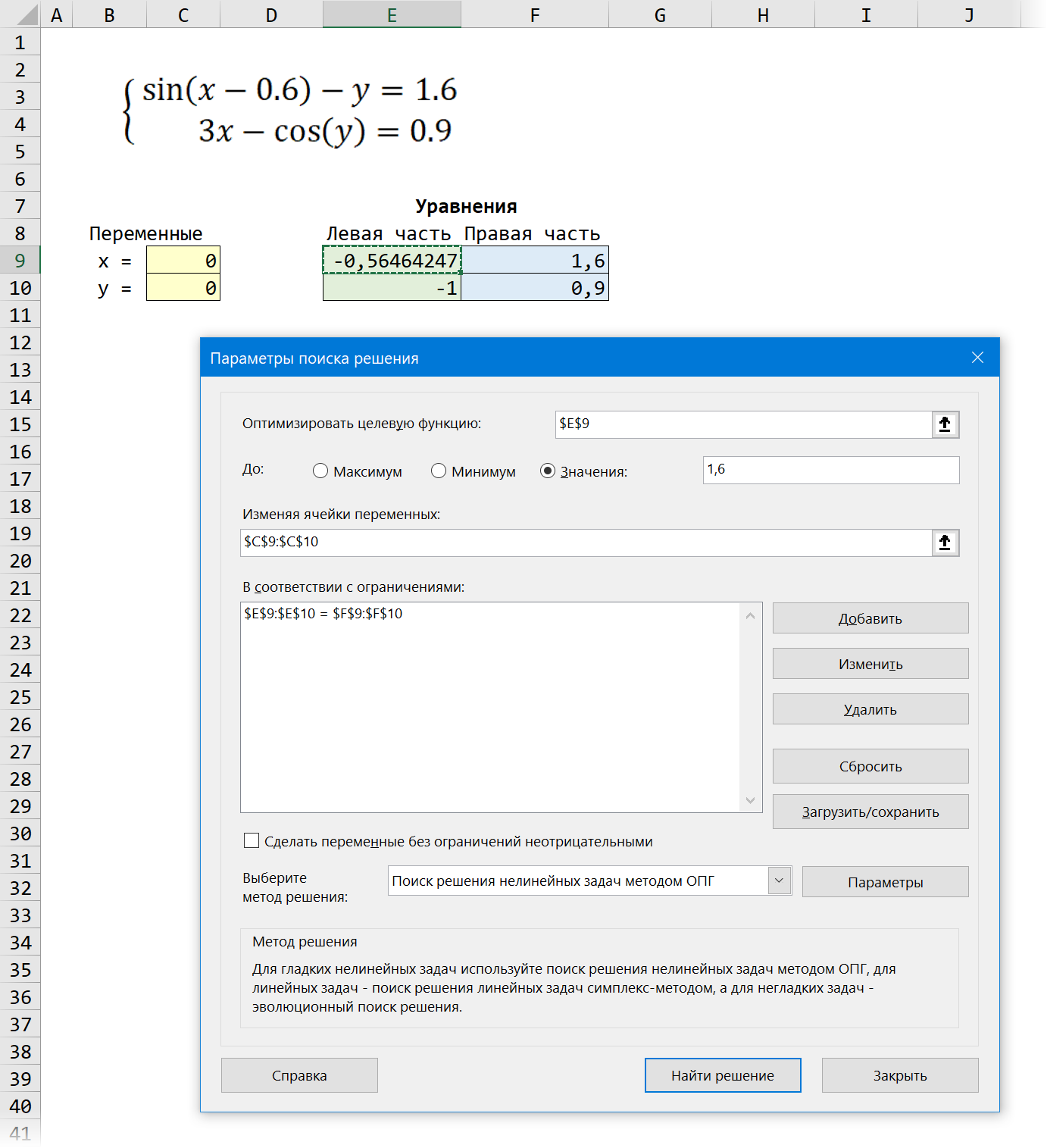
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
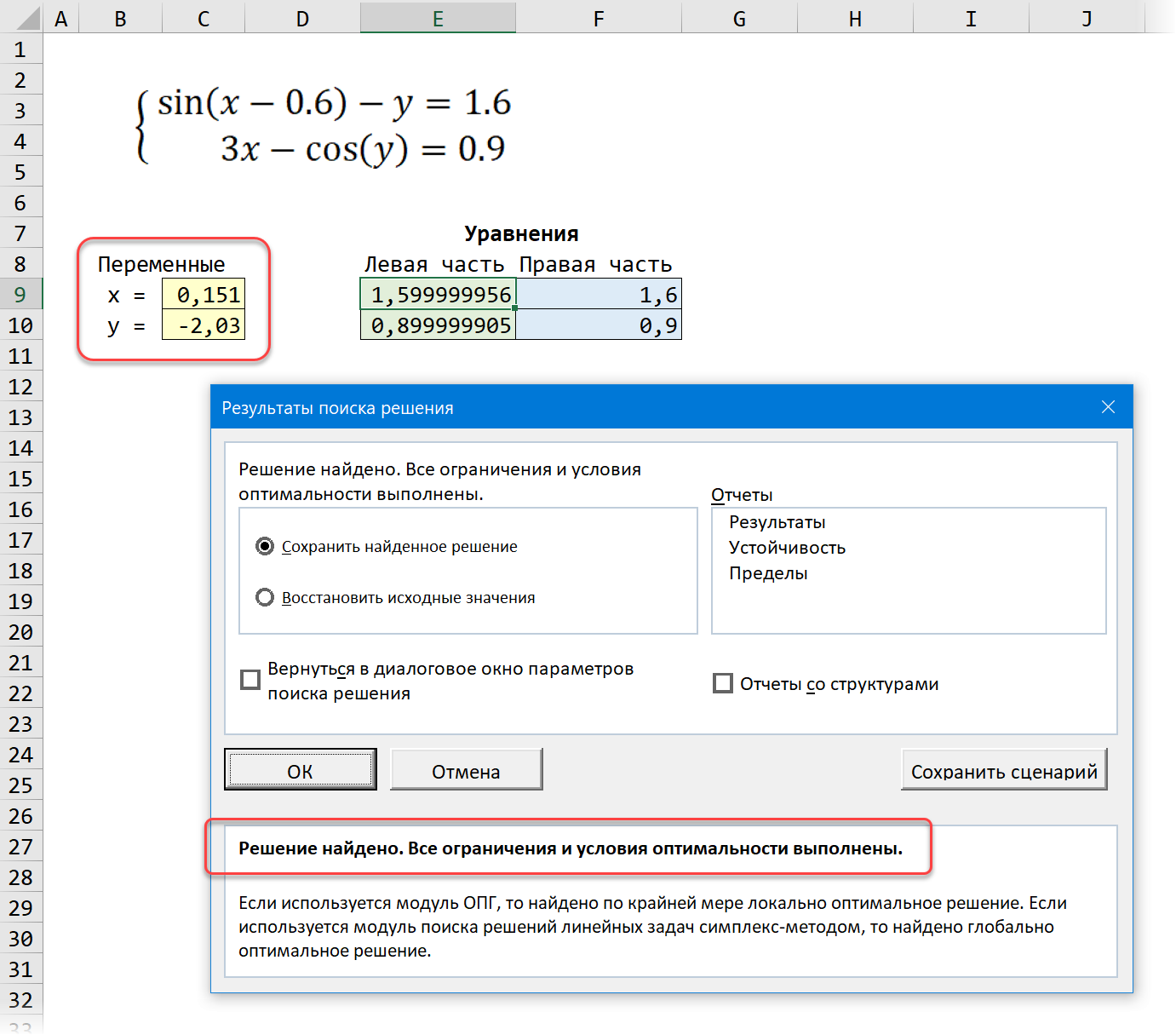
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options) .
Источник: www.planetaexcel.ru
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.

- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».


Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:

- Значения элементов введем в ячейки Excel в виде таблицы.

- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.

- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.

- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.

- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.

- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.

- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.

- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: .

- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
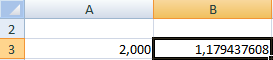
Корень на заданном промежутке один.
Источник: exceltable.com