Презентация 11 класса по предмету «Математика» на тему: «Способы решения уравнений с помощью компьютера». Скачать бесплатно и без регистрации. — Транскрипт:
1 Урок информатики 11 класс Разработала: учитель информатики МБОУ г. Астрахани «СОШ54» Кононенко Н.В.
2 Цели урока: расширение и систематизация знаний учащихся о применении компьютера для решения задач, способах решения алгебраических уравнений с помощью компьютера. Совершенствование навыков составления и реализации программ на языке Турбо Паскаль, навыков использования программы Excel для решения задач. Создание условий для развития исследовательской, творческой, познавательной деятельности учащихся.
3 Задача: решить уравнение вида Какими способами можно решить уравнение? Что значит решить уравнение аналитически? Что значит решить уравнение графически?
4 Из каких этапов складывается решение задач с помощью ПК? Постановка задачи Разработка формальной модели Построение компьютерной модели Компьютерный эксперимент Анализ результатов Корректировка модели
Как решать уравнение?|Решение уравнений с помощью программы PhotoMath
5 Какие 2 пути построения компьютерной модели вам известны? Компьютерная модель На языке программирования Модель, созданная с помощью приложения
6 Из каких этапов складывается графическое решение уравнения с помощью программы Excel? Построение таблицы значений Построение графиков функций Определение корней уравнения(точек пересечения графиков)
7 Решим уравнение вида sin(2*α)=0.5*(sin(α)+cos(α)) Этапы решения уравнения с помощью численных методов: отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения; вычисление корня с заданной точностью.
8 Численные методы приближенного вычисления корней уравнения: Метод половинного деления Метод касательных Метод хорд Метод секущих Метод хорд и касательных
9 Метод половинного деления Решение уравнения f(x)=0 заключается в определении значения переменной х, обращающей f(x) в «0». Пусть на интервале изоляции корня [a, b] изолирован действительный корень уравнения f(x)=0. На интервале изоляции корня [a, b] определяется точка С, являющаяся серединой этого отрезка, c=(a+b)/2. Вычисляется значение функции f(x) в точках a, b, c. Если f(c)=0, то С- точный корень уравнения f(x)=0. В противном случае из двух образовавшихся отрезков [a, c] и [c, b] выбирается тот, на концах которого функция принимает противоположные знаки и новый отрезок обозначается через [a, b]. За результирующее значение корня принимается величина X=(a+b)/2, где a и b удовлетворяют Abs (b-a)
10 Решение трансцендентных уравнений методом половинного деления.
11 Практическое закрепление. 1 группа: Отделяет корни уравнения: составляет таблицу значений функции на интервале от 0 до 1,95 с шагом 0,15 и выделяет соседние значения аргументов для которых значения функции имеют разные знаки, то есть значения аргументов между которыми находится нуль функции. 2 группа: Определяет корни графически на интервале от 0 до 1,95 с шагом 0,15. 3 группа: В среде Турбо Паскаль реализует составленную программу и определяет корни с точность 0,001.
Приложения для Учёбы | Полезно!
12 Подведение итогов занятия Какие способы решения уравнений рассмотрели на уроке? Из каких этапов складывается графическое решение с использованием программы Excel? Какие численные методы используются для решения уравнений? В чем сущность метода половинного деления? Какой способ организации действий использован в составленной программе?
В чем преимущество численных методов перед графическим методом отыскания корней? Что не учитывает программа составленная на уроке?
13 Домашнее задание: модернизировать программу, предусмотрев возможность отыскания интервалов, содержащих корень.
Источник: www.myshared.ru
XI Международная студенческая научная конференция Студенческий научный форум — 2019
Визуализация решений однородных уравнений средствами компьютерной математики
Гусев А.Д. 1
1 ГОУ ВО МО «ГСГУ»
Работа в формате PDF
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Применение компьютера, как в начале истории ЭВМ, так и поныне, в основном, заключается в математических и научно-технических вычислениях. Компьютер сам по себе не упрощает математические расчеты, а лишь позволяет существенно повысить скорость их выполнения и сложность решаемых задач, в том числе с использованием удобного ввода исходных данных и вывода результатов.
В конце 90-х годов двадцатого века с появление новых высокопроизводительных персональных ЭВМ появился новый класс прикладного программного обеспечения — интегрированные математические программные системы для научно-технических расчетов, такие как: Eureka, MatLAB, MathCad , Maple, Mathematica и др. Главное их преимущество перед классическими системами программирования заключалось в том, что необходимые для решения задач численного моделирования функции и процедуры уже входили в их состав, а также в них изначально был использован интуитивный и понятный пользовательский интерфейс, ориентированный на ученых и инженеров.
Большое число подобных разработок свидетельствует о значительном интересе к ним во всем мире и бурном развитии компьютерных математических систем. Рассмотрим систему MathCad ориентированную на массового пользователя — от ученика начальных классов до академика.
Актуальность данной темы « Визуализация решений однородных уравнений средствами компьютерной математики » определяется её огромным прикладным значением, её ролью и местом в школьном курсе информатики и математики, а также для решения задач разного типа.
Целью данной работы является изучение пакета MathCad как средства решения однородных уравнений (первой и второй степени) и реализация с его помощью нескольких конкретных примеров и их реализация в виде интерактивного документ.
Для этого необходимо выполнить следующие задачи:
изучить основные возможности пакета MathCad применительно к решению однородных уравнений первого и второго порядка;
проанализировать несколько типов задач с однородными уравнениями, которые возможно решить средствами MathCad (аналитически и графическим способами) в рамках данной работы;
реализовать эти задачи средствами MathCad .
Рассмотрим несколько примеров решения однородных уравнений с применением математического пакета MachCad (аналитически и графически).
Пример 1. Решите уравнение: Найдите
Разделим уравнение на . Нужно всегда помнить, что делить (и умножать) на переменную мы можем только тогда, когда мы уверены, что эта переменная не может быть равна 0. У нас по условию не может быть равен 0 . Поэтому мы можем смело делить на . Произведя замену , мы получим простое квадратное уравнение: Произведя обратную замену, получим ответ:
Решение уравнения с помощью программы MathCad :
Пример 2. Решите уравнение:
Перепишем уравнение в виде Разделим обе расти уравнения почтенно на : После упрощения приходим к уравнениюЭто уравнение сводится к квадратному уравнению при помощи замены где . Оба корня квадратного уравнения удовлетворяют условию .
Решение уравнения с помощью программы MathCad :
Пример 3. Решите уравнение:
Обе части уравнения делим на (этот логарифм обращается в нуль, когда , то есть при . Но нуль не входит в ОДЗ, следовательно, деление на не ведет к потере корней).
Делим обе части уравнения на
Обратная замена: Оба корня не входят в ОДЗ.
Первый корень не входит в ОДЗ. Ответ.
Решение уравнения с помощью программы MathCad :
Пример 4. Решите систему уравнений:
Зная , легко сразу найти , учитывая, что . Используя это, найдем , а затем .
Решение уравнения с помощью программы MathCad :
Пример 5. Решите систему уравнений графически :
Умножим обе части второго уравнения на 2 и сложим его с первым. В результате получим:
По графику получается:
Разобранные примеры показывают возможности системы компьютерной математики. Полученные в результате выполнения рабочие листы можно использовать для решения типовых уравнений с разными числовыми коэффициентами. Данные задачи можно использовать на уроках математики или во внеурочной деятельности на интегрированных курсах по математике и информатике.
Бекаревич, А. Н. Уравнения в школьном курсе математики. Книга для учителей математики / А. Н. Бекаревич. – Минск: Народная асвета, 1968. – 152 с.
Васильев, А. Н. Mathcad 15 на примерах (+ CD-ROM) [Текст] / А. Н. Васильев. – СПб.: БХВ-Петербург, 2016. – 528 с.
Источник: scienceforum.ru
Методы решения кубических уравнений
В области комплексных чисел, согласно основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом кратности). Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпывается тремя, которые легко различаются с помощью дискриминанта [2]:
· Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
· Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо, все три корня совпадают, образуя корень кратности 3.
Корни кубического уравнения 
связаны с коэффициентами 
следующим образом:
Исходя из основных свойств решения кубических уравнений, необходимо дать определение понятию «комплексное число». Комплексные числа — числа вида x + y , где x и y – вещественные числа, i – мнимая единица , то есть: i 2 = –1. Числа x = Â (z) ( или Re z ) и y = Á (z) ( или Im z ) называются соответственно вещественной и мнимой частями z . Множество всех комплексных чисел обозначается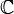 
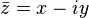называется сопряжённым к z . [1]
Наиболее распространенный метод решения кубических уравнений – метод перебора. [2] Сначала путём перебора находится один из корней уравнения (например, x 1 ). Вторая стадия решения – это деление многочлена ax 3 + bx 2 + cx + d на двучлен x – x 1 и решение полученного квадратного уравнения.
Алгоритм решения кубических уравнений с использованием формулы Кардано
Рассмотрим алгоритм нахождения всех корней кубического уравнения 
на основе описанной выше формулы, а также ее тригонометрической интерпретации. [3,4] Приведем исходное уравнение к каноническому виду. Для этого с делаем замену переменного по формуле 
: 
. Раскрыв скобки в левой части уравнения, получим: 
. Уравнение приведено к каноническому виду:
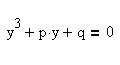
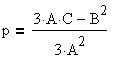
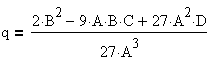
Дискриминантом уравнения 
называется число 
. Найдем решение полученного уравнения в виде:
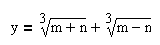
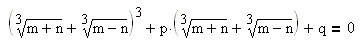
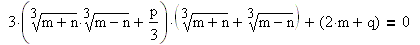
Число удовлетворяет этому равенству, если числа m и n удовлетворяют системе из двух уравнений:
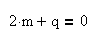
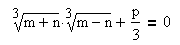
Находим числа m и n:
Дальнейшее решение зависит от знака дискриминанта S.
1. Пусть дискриминант меньше нуля. Тогда уравнение имеет три различных корня.
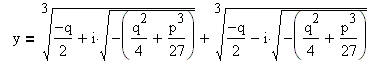
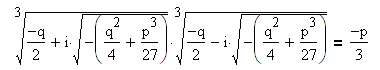
Найдём модуль комплексных чисел :
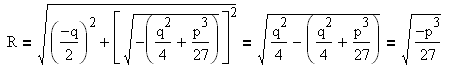
Аргумент числа равен (в зависимости от знака q):
· Если 
, то 
· Если 
, то 
· Если 
, то 
Для k=0, k=1, k=2 получаем решение:
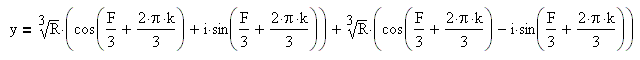
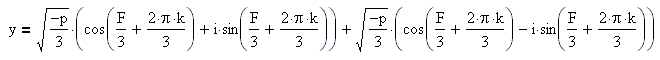
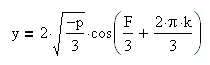
Итак, если дискриминант меньше нуля, то уравнение имеет три различных действительных корня:
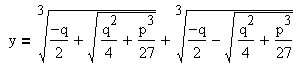
2. Пусть дискриминант больше нуля. Тогда уравнение имеет один действительный корень и два комплексно-сопряжённых.
При этом для любых комплексных значений корней необходимо выполнение условия: .
Примем аргумент F действительных чисел, стоящих под знаком кубического корня, равным нулю. При этом модули этих чисел могут принимать отрицательное значение. Аргумент кубического корня будет принимать 3 значения: 0, 2*π/3, 4*π/3. Каждое решение y=y1, y=y2, y=y3 будет состоять из суммы двух комплексных чисел .
Число z1 находится в группе из трёх чисел:
Число z2 находится в группе из трёх чисел:
Для действительных значений кубических корней выполняется обозначенное выше условие. Поэтому действительный корень уравнения 
. Учитывая равенство 
, получим два комплексно сопряжённых корня: 
, 
.
Итак, если дискриминант больше нуля, то уравнение имеет один действительный корень и два комплексно-сопряжённых корня:
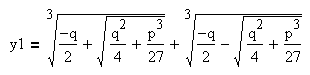
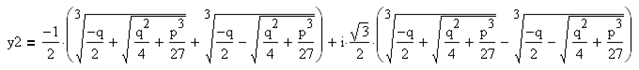
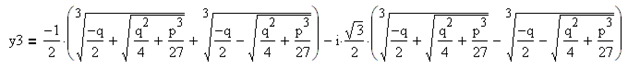
3. Дискриминант равен нулю. В этом случае уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом. Рассуждая точно так же, как в случае с положительным дискриминантом, учитывая равенство , из формул корней уравнения с положительным дискриминантом получим:
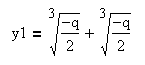
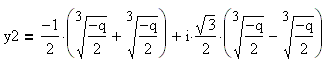
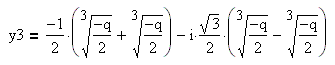
Итак, если дискриминант равен нулю, то уравнение имеет три действительных корня, и два корня из трёх обязательно совпадают друг с другом: .
Теперь получим решение исходного кубического уравнения . Дискриминант этого уравнения равен:
В зависимости от знака дискриминанта S возможны три случая:
· Если , то:
· Если , то:
· Если , то:
Реализация алгоритма в объектно-ориентированной среде программирования Delphi
Авторами статьи была создана программа в среде Delphi для решения кубических уравнений с использованием формулы Кардано по разработанному алгоритму, описанному выше.
Рис. 1 . Интерфейс программы для решения кубических уравнений.
Для решения уравнения пользователю необходимо ввести коэффициенты уравнения. Результат работы программы – коэффициенты уравнения в канонической форме (p и q), дискриминант (Q) и корни уравнения. Для создания интерфейса использовались следующие компоненты среды Delphi [5]:
· Label – для информирования пользователя о назначении программы, обозначения предназначения полей ввода – вывода;
· Button – для реализации основных действий программы (решения уравнения, очистки полей ввода-вывода, закрытия программы);
· Edit – для организации ввода-вывода данных;
· Panel и GroupBox – для группировки элементов на форме программы.
Рассмотрим код основных процедур программы.
Для решения уравнения необходимо объявить следующие переменные:
· A,B,C,D – коэффициенты исходного уравнения;
· p,q – коэффициенты преобразованного уравнения;
· F – аргумент комплексного корня;
· Re, Im – действительная и мнимая части комплексного корня;
· x1,x2,x3,y1,y2 – корни уравнения.
В программе предусмотрен контроль корректности ввода данных:
if (edit1.Text=») or (edit2.Text=») or (edit3.Text=») or (edit4.Text=») then
Showmessage(‘Введите все коэффициенты уравнения’);
Процедуры Clear_Koeffs и Clear_Results осуществляют очистку полей ввода-вывода.
Процедура вычисления коэффициентов и дискриминанта преобразованного уравнения имеет следующий вид:
edit5.Text := FloatToStr(p); edit6.Text := FloatToStr(q);
Вычисление корней уравнения происходит в зависимости от знака дискриминанта:
· Если дискриминант меньше нуля:
if q>0 then F:=Arctan(-2*Sqrt(-QQ)/q)+Pi;
if q=0 then F:=Pi/2;
if q=0 then x3:=-B/A/3;
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
· Если дискриминант больше нуля:
if QQ>0 then begin
if -q/2+Sqrt(QQ)>0 then y1:=exp(ln(abs(-q/2+Sqrt(QQ)))/3);
if -q/2+Sqrt(QQ)=0 then y1:=0;
if -q/2-Sqrt(QQ)>0 then y2:=exp(ln(abs(-q/2-Sqrt(QQ)))/3);
if -q/2-Sqrt(QQ)=0 then y2:=0;
x1:=y1+y2-B/A/3; Re:=-(y1+y2)/2-B/A/3; Im:=(y1-y2)*Sqrt(3)/2;
Edit9.Text := FloatToStr(Re)+’ + i * ‘+FloatToStr(Im);
Edit10.Text:= FloatToStr(Re)+’ — i * ‘+FloatToStr(Im);
· Если дискриминант равен нулю:
if QQ=0 then begin
if q>0 then y1:=-exp(ln(abs(-q/2))/3);
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
В программе также организован программный контроль ввода коэффициентов. Для этого создан обработчик события KeyPress для соответствующих элементов типа Edit [6]:
if not (Key in [‘-‘, ‘1’..’9′, #8]) then Key := #0.
В рамках проведенного исследования было рассмотрено несколько способов решения кубических уравнений, в том числе, с использованием формулы Кардано. Были изучены различные нюансы применения этого метода, а также проведено исследование зависимости получаемых результатов от знака кубического дискриминанта. В статье также приведен подробный алгоритм, разработанный авторами статьи, на основе тригонометрической интерпретации формулы Кардано, а также рассмотрены основные процедуры созданного программного обеспечения в объектно-ориентированной среде Delphi.
Существует довольно много проблем в различных научных областях, решение которых сводится к изучению методов решения уравнений третьей и выше степеней. Таким образом, можно сделать вывод, что актуальность проведенного исследования заключается в практическом применении рассмотренных методов, а также созданного программного обеспечения как при изучении некоторых тем математики, физики в школе и ВУЗах, так и при решении прикладных задач из различных областей.
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. – М.: Наука, 1986.
2. Омельченко В.П., Э.В.Курбатова. Математика: учебное пособие. – Ростов н/Д.: Феникс, 2005.
3. Пичурин Л.Ф. За страницами учебника алгебры. – М.: Просвещение, 1990.
4. Корн Г., Корн Т. Справочник по математики для научных работников и инженеров. – М.: Наука, 1973.
5. Фленов М.Е. Библия Delphi. – С-Пб: БХВ-Петербург, 2011.
6. Архангельский А.Я. Delphi 7. Справочное пособие. – М.: Бином, 2004.
Поступила в редакцию 07.04.2014 г.
2006-2019 http://jurnal.org/articles/2014/mat4.html» target=»_blank»]jurnal.org[/mask_link]