Стоит задача найти оптимальное решение для игры пятнашки puzzle 15 для игрового поля 3 на 3, в принципе мне кажется что программа практически готова, но есть одно маленькое но: решается только простые состояния где требуется малое кол-во перестановок, к примеру < 1, 2, 3, 4, 5, 6, 0, 7, 8 >; более сложные же (например < 1, 0, 2, 4, 6, 3, 7, 5, 8 >;) не приходят к решению так как можно сказать что программа забивается в угол и не может оттуда выйти вот я и не могу никак понять где что подправить чтобы программы выходила из таких ситуаций также не совсем понял какой тип указать при возврате массива из функции поэтому поставил auto
auto from_vector_to_array(vector int len = N; int vec_array[N][N]; int count = 0; for (int i = 0; i < len; i++) for (int j = 0; j < len; j++) < vec_array[i][j] = this_vector[count]; ++count; >return vec_array; >
метрика самая простая, двигаюсь в ту сторону где наименьшее кол-во стоящих на своих местах элементов код онлайн https://rextester.com/live/LWLCPI90421
Как собрать пятнашки 3х3 за минуту: МАЛАЯ #Shorts
#include «pch.h» #include #include #include #include #define N 3 using namespace std; int max_depth = 100; bool is_solved = false; auto from_vector_to_array(vector int len = N; int vec_array[N][N]; int count = 0; for (int i = 0; i < len; i++) for (int j = 0; j < len; j++) < vec_array[i][j] = this_vector[count]; ++count; >return vec_array; > // A utility function to count inversions in given // array ‘arr[]’. Note that this function can be // optimized to work in O(n Log n) time. The idea // here is to keep code small and simple. int getInvCount(int arr[]) < int inv_count = 0; for (int i = 0; i < N * N — 1; i++) < for (int j = i + 1; j < N * N; j++) < // count pairs(i, j) such that i appears // before j, but i >j. if (arr[j] arr[i] arr[i] > arr[j]) inv_count++; > > return inv_count; > // find Position of blank from bottom int findXPosition(int puzzle[N][N]) < // start from bottom-right corner of matrix for (int i = N — 1; i >= 0; i—) for (int j = N — 1; j >= 0; j—) if (puzzle[i][j] == 0) return N — i; > // This function returns true if given // instance of N*N — 1 puzzle is solvable bool isSolvable(int puzzle[N][N]) < // Count inversions in given puzzle int invCount = getInvCount((int*)puzzle); // If grid is odd, return true if inversion // count is even. if (N 1); else // grid is even < int pos = findXPosition(puzzle); if (pos 1); else return invCount >> int find_index_number(vector for (int i = 0; i < this_vector.size(); ++i) < if (number == this_vector[i]) return i; >> void go_right(vector int zero_index = find_index_number(this_vector, 0); if (zero_index == 0 || zero_index == 1 || zero_index == 3 || zero_index == 4 || zero_index == 6 || zero_index == 7) < switch (zero_index) < case 0: swap(this_vector[zero_index], this_vector[1]); break; case 1: swap(this_vector[zero_index], this_vector[2]); break; case 3: swap(this_vector[zero_index], this_vector[4]); break; case 4: swap(this_vector[zero_index], this_vector[5]); break; case 6: swap(this_vector[zero_index], this_vector[7]); break; case 7: swap(this_vector[zero_index], this_vector[8]); break; >> > void go_left(vector int zero_index = find_index_number(this_vector, 0); if (zero_index == 1 || zero_index == 2 || zero_index == 4 || zero_index == 5 || zero_index == 7 || zero_index == 8) < switch (zero_index) < case 1: swap(this_vector[zero_index], this_vector[0]); break; case 2: swap(this_vector[zero_index], this_vector[1]); break; case 4: swap(this_vector[zero_index], this_vector[3]); break; case 5: swap(this_vector[zero_index], this_vector[4]); break; case 7: swap(this_vector[zero_index], this_vector[6]); break; case 8: swap(this_vector[zero_index], this_vector[7]); break; >> > void go_down(vector int zero_index = find_index_number(this_vector, 0); if (zero_index == 0 || zero_index == 1 || zero_index == 2 || zero_index == 3 || zero_index == 4 || zero_index == 5) < switch (zero_index) < case 0: swap(this_vector[zero_index], this_vector[3]); break; case 1: swap(this_vector[zero_index], this_vector[4]); break; case 2: swap(this_vector[zero_index], this_vector[5]); break; case 3: swap(this_vector[zero_index], this_vector[6]); break; case 4: swap(this_vector[zero_index], this_vector[7]); break; case 5: swap(this_vector[zero_index], this_vector[8]); break; >> > void go_up(vector int zero_index = find_index_number(this_vector, 0); if (zero_index == 3 || zero_index == 4 || zero_index == 5 || zero_index == 6 || zero_index == 7 || zero_index == 8) < switch (zero_index) < case 3: swap(this_vector[zero_index], this_vector[0]); case 4: swap(this_vector[zero_index], this_vector[1]); case 5: swap(this_vector[zero_index], this_vector[2]); case 6: swap(this_vector[zero_index], this_vector[3]); case 7: swap(this_vector[zero_index], this_vector[4]); case 8: swap(this_vector[zero_index], this_vector[5]); >> > bool is_state_identical(vector first_vector, vector second_vector) < for (int i = 0; i < first_vector.size(); i++) < if (first_vector[i] != second_vector[i]) return false; >return true; > void display_state(vector for (int i = 0; i < this_vector.size(); i++) < cout cout bool check_history(vector history) < if (history.size() == 0) return false; for (int i = 0; i < history.size(); ++i) < if (this_vector == history[i]) return true; >return false; > int amount_unmatching_left(vector final_vector) < int zero_index = find_index_number(start_vector, 0); int count = 0; if (zero_index == 1 || zero_index == 2 || zero_index == 4 || zero_index == 5 || zero_index == 7 || zero_index == 8) < switch (zero_index) < case 0: if (start_vector[0] != final_vector[0]) ++count; case 1: if (start_vector[1] != final_vector[1]) ++count; case 3: if (start_vector[3] != final_vector[3]) ++count; case 4: if (start_vector[4] != final_vector[4]) ++count; case 6: if (start_vector[6] != final_vector[6]) ++count; case 7: if (start_vector[7] != final_vector[7]) ++count; >> return count; > int amount_unmatching_right(vector final_vector) < int zero_index = find_index_number(start_vector, 0); int count = 0; if (zero_index == 0 || zero_index == 1 || zero_index == 3 || zero_index == 4 || zero_index == 6 || zero_index == 7) < switch (zero_index) < case 0: if (start_vector[1] != final_vector[1]) ++count; case 1: if (start_vector[2] != final_vector[2]) ++count; case 3: if (start_vector[4] != final_vector[4]) ++count; case 4: if (start_vector[5] != final_vector[5]) ++count; case 6: if (start_vector[7] != final_vector[7]) ++count; case 7: if (start_vector[8] != final_vector[8]) ++count; >> return count; > int amount_unmatching_up(vector final_vector) < int zero_index = find_index_number(start_vector, 0); int count = 0; if (zero_index == 3 || zero_index == 4 || zero_index == 5 || zero_index == 6 || zero_index == 7 || zero_index == 8) < switch (zero_index) < case 0: if (start_vector[0] != final_vector[0]) ++count; case 1: if (start_vector[1] != final_vector[1]) ++count; case 3: if (start_vector[2] != final_vector[2]) ++count; case 4: if (start_vector[3] != final_vector[3]) ++count; case 6: if (start_vector[4] != final_vector[4]) ++count; case 7: if (start_vector[5] != final_vector[5]) ++count; >> return count; > int amount_unmatching_down(vector final_vector) < int zero_index = find_index_number(start_vector, 0); int count = 0; if (zero_index == 0 || zero_index == 1 || zero_index == 2 || zero_index == 3 || zero_index == 4 || zero_index == 5) < switch (zero_index) < case 0: if (start_vector[3] != final_vector[3]) ++count; case 1: if (start_vector[4] != final_vector[4]) ++count; case 3: if (start_vector[5] != final_vector[5]) ++count; case 4: if (start_vector[6] != final_vector[6]) ++count; case 6: if (start_vector[7] != final_vector[7]) ++count; case 7: if (start_vector[8] != final_vector[8]) ++count; >> return count; > void find_solution(vector final_vector, int deepth, vector srand(time(0)); if (deepth >max_depth || is_solved == true) < exit(0); >if (is_state_identical(current_vector, final_vector)) < cout //int where_to_go = rand() % 4; int where_to_go, left, right, up, down, maximum; left = amount_unmatching_left(current_vector, final_vector); right = amount_unmatching_right(current_vector, final_vector); up = amount_unmatching_up(current_vector, final_vector); down = amount_unmatching_down(current_vector, final_vector); maximum = max(max(max(left, right), up), down); if (maximum == left) where_to_go = 0; if (maximum == right) where_to_go = 1; if (maximum == up) where_to_go = 2; if (maximum == down) where_to_go = 3; vector temp_vector(current_vector.size()*current_vector.size()); switch (where_to_go) < case 0: temp_vector = current_vector; go_left(temp_vector); if (!check_history(temp_vector, history)) < current_vector = temp_vector; history.push_back(current_vector); display_state(current_vector); >find_solution(current_vector, final_vector, deepth + 1, history); case 1: temp_vector = current_vector; go_right(temp_vector); if (!check_history(temp_vector, history)) < current_vector = temp_vector; history.push_back(current_vector); display_state(current_vector); >find_solution(current_vector, final_vector, deepth + 1, history); case 2: temp_vector = current_vector; go_up(temp_vector); if (!check_history(temp_vector, history)) < current_vector = temp_vector; history.push_back(current_vector); display_state(current_vector); >find_solution(current_vector, final_vector, deepth + 1, history); case 3: temp_vector = current_vector; go_down(temp_vector); if (!check_history(temp_vector, history)) < current_vector = temp_vector; history.push_back(current_vector); display_state(current_vector); >find_solution(current_vector, final_vector, deepth + 1, history); > > int main() < int size = 3; vector start_state(size*size); vector final_state(size*size); vector history; final_state = < 1, 2, 3, 4, 5, 6, 7, 8, 0 >; //start_state = < 1, 0, 2, 4, 6, 3, 7, 5, 8 >; start_state = < 1, 2, 3, 4, 5, 6, 0, 7, 8 >; display_state(start_state); if (isSolvable(from_vector_to_array(start_state))) < cout else < cout //cout
Источник: ru.stackoverflow.com
Игра в пятнашки

Пятнашки – одна из известнейших миру головоломок. Она представляет набор, в который входит квадратная коробка, сторона которой равна 4 сторонам костяшки, то есть. 4х4. Внутри этой коробки 15 квадратных костяшек. В коробке остается 1 свободное место под одну костяшку.
Цель игры – упорядочивание костяшек по порядку. Концом игры считается, когда все костяшки от 1 до 15 стоят друг за другом.
Игра поможет вам развить память и логическое мышление. У вас будет развиваться возможность просчитывать ходы вперед без ошибок. Сыграем?
Видео: как играть в пятнашки?
Посмотрите видео-пример по прохождению игры Пятнашки:
Онлайн игра в пятнашки
Номерки уже разбросаны в случайном порядке. Нажатием на костяшку, Вы сможете ее передвигать в направлении свободной клетки. Постарайтесь распределить их по порядку, используя наименьшее количество ходов.
Эту игру можно купить практически в любом магазине детских или настольных игрушек. Материал, из которого сделаны пятнашки, может быть различный, как дерево, так и металл или пластик.

Правила игры
Если Вы играете в первый раз, то, наверное, задаетесь вопросом «как собрать пятнашки» или «как играть в пятнашки»? Это головоломка не из простых, и Вам потребуется логика и терпение для их собирания. В среднем людям приходится тратить 200-300 ходов на решение задачи. Попробуйте и Вы! После небольшой тренировки у вас получится куда быстрее, не сомневайтесь!
Алгоритм «Как собрать пятнашки»?
Как-то раз, собирая пятнашки, заметил, что чем меньше поле ячеек в игре пятнашки, тем проще их собрать. Получается, что проще всего собрать пятнашки размером 3х3 ячейки, чем например, пятнашки размером 4х4.
Пятнашки размером 3х3 элемента собираются очень легко, особенно если отсортировать все костяшки по порядку вокруг поля:
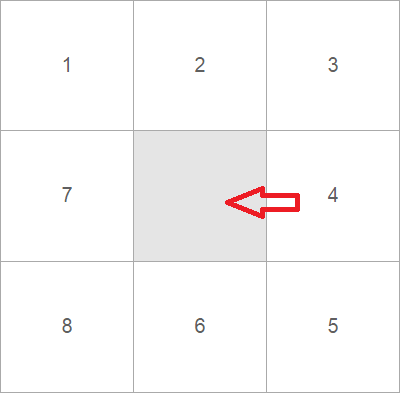
Для этого нужно перемещать самую первую костяшку по кругу против часовой стрелки, и при первой же возможности поставить следом за первой костяшкой, вторую, потом третью, собрав, таким образом, паровозик из костяшек от первой до последней.
Главное, чтобы последние две костяшки, в данном случае 7 и 8 стояли наоборот, то есть. паровозик из цифр должен выглядеть так: 1 2 3 4 5 6 8 7. Если мы поделим этот паровозик на строки, то как раз и получим собранные пятнашки.
Посмотрите еще раз на картинку выше, там костяшки 1 2 3 уже стоят на своем месте, осталось всего-то переместить костяшки 4 5 6 на второй ряд. В результате этого переноса костяшки 7 и 8 уже будут стоять в третьем ряду в нужном порядке.
Разделяй и властвуй
Это очень простой способ сбора пятнашек, однако, собрать таким способом пятнашки размером 4х4 ячейки уже намного сложнее, не говоря уже о пятнашках бОльшего размера.Если приосмотреться к этой игре внимательно, то можно увидеть, что ничего сложного нет, если разделить поле 4х4 ячейки на 3 части и собрать эти 3 части по отдельности.
Часть первая, костяшки 1 2 3 4
В первую очередь лучше собрать костяшки 1 2 3 4 и расположить их на своем месте, после чего просто “забыть” про них, будто их нет:
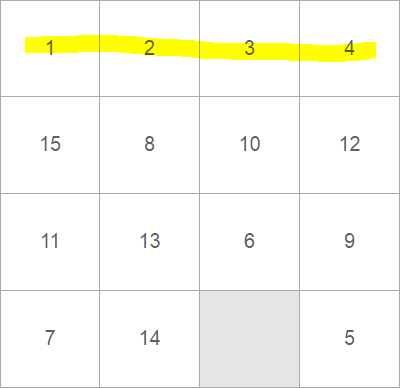
После того как мы про них “забыли”, дальше остается собрать пятнашки с размером поля уже 4х3, вместо 4х4.
Часть вторая, костяшки 5 9 13
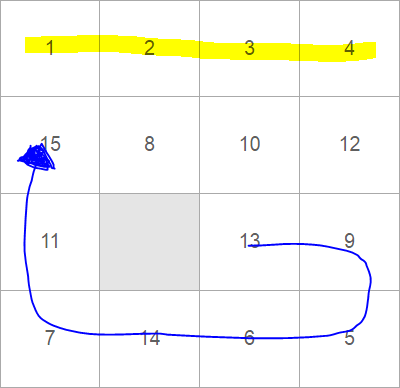
Теперь нам нужно собрать костяшки 5 9 13 в паровозик и поставить их сбоку слева.
Часть третья, оставшиеся костяшки
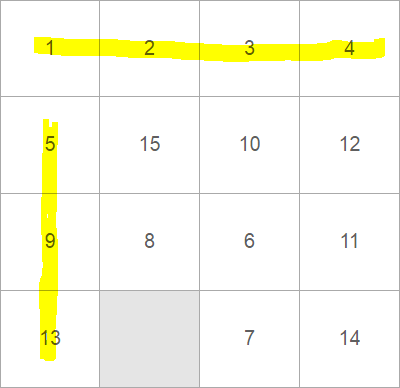
Теперь, когда мы уже поставили костяшки 1 2 3 4 и 5 9 13 на свои места, рабочее поле уменьшилось до размеров 3х3, и осталось только собрать пятнашки размером 3х3:
Единственное отличие заключается только в номерах костяшек, которые нужно отсортировать так же по возрастанию, поменяв последние две костяшки наоборот, чтобы получился паровозик: 6 7 8 10 11 12 15 14, который так же разделится на 3 ряда:
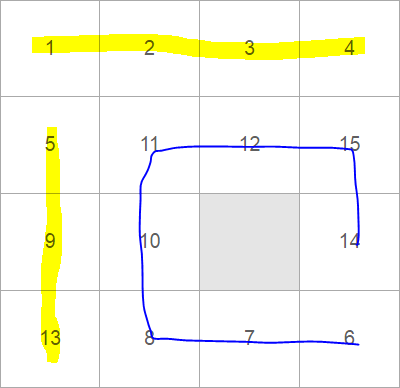
Проблема может быть только в том, что костяшки могут встать не по порядку. Вместо паровозика из цифр 6 7 8 10 11 12 15 14 может получиться последовательность 6 7 8 10 11 12 14 15. В таком случае нужно будет постараться поменять эти костяшки местами. Зачастую для этого приходится ломать уже построенные костяшки 5 9 13 или 1 2 3 4, но зато они потом так же быстро выстраиваются снова.
Скачать
Скачать игру пятнашки на свой компьютер Вы сможете по ссылке, расположенной ниже. Скачав игру, Вы сможете решать головоломку без интернета, нежели Вы будете решать ее на сайте.
Системные требования: Windows XP, Vista, 7, 8, 8.1, 10.
Подвижная игра пятнашки
Количество участников может быть различным (оптимальное 4-12). Отметим границу для игры в пятнашки, к примеру 7 метров в длину и ширину.
Выбирают водящего человека, который как в салках бегает за другими ребятами. Остальные же игроки располагаются по периметру квадрата. Выход за пределы запрещен. Цель водящего – догнать других игроков и «запятнать» их. Запятнанные игроки немедленно покидают поле.
Игра продолжается пока не будут запятнаны все игроки.После конца кона можно начать еще раз, выбрав другого водящего.
История появления игры
Авторство игры принадлежит Ною Палмеру Чепмэну. Еще в далеком 1874 году Ной показывал свою игру знакомым, которая включала в себя квадратную коробку, сторона которой равна 4 сторонам костяшки, в свою очередь костяшек 15 одинаковых квадратных штук. В коробке остается 1 свободное место под одну костяшку. Однако, целью игры было перемещение костей так, чтобы в каждом ряду была сумма 34.
Особое внимание было к игру с 1880. Именно в этом году некто Чарльз Певи, установил денежное вознаграждение за решение данной задачи. Популярность игры мгновенно выросла. С тех пор правила поменялись и теперь они такие, как описаны выше.Существуют различные варианты игры c разными размерами:
Пятнашки 3х3
Пятнашки 4х4
Пятнашки 5х5
Похожие игры
Существуют похожие игры, в которые вы сможете играть онлайн. Игры взяты с сайта нашего партнера BrainApps, на котором вы сможете найти и множество других интересных и увлекательных игр. Например:
Игра «Анаграммы»
Анаграммы помогут развить такие качества как: внимание, концентрация, скорость мысли, скорочтение. В этой игре Вам предстоит выбрать 1 вариант из 4, в которым перемешаны только те буквы, которые входят в состав данного слова. В каждом раунде дается новое слово. Помните, что время ограничено! Чем быстрее вы будете искать ответ – тем больше очков получите в конце игры.
А если вы хотите играть с сохранением статистики результатов, то предлагаем игру от нашего партнера BrainApps, нужно только зарегистрироваться и около 30 бесплатных развивающих игр Ваши:
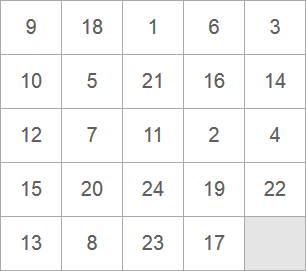
Игра «Таблицы Шульте»
Таблица Шульте — таблица случайно расположенных чисел, обычно размером 5×5 элементов и обычно состоит из цифр и букв. Требуется отмечать представленные числа в циклической последовательности: минимальное черное, максимальное красное. Это упражнение способствует развитию скорочтения, потому что улучшает периферийное зрение, так же помогает развивать память и устный счет. Игру Вы сможете найти на сайте нашего партнера BrainApps и в статье на этом сайте Таблицы Шульте.

Остались вопросы?
Источник: cepia.ru
hardenchant/15_solver
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags
Nothing to show
Name already in use
A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
- Local
- Codespaces
HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.
Sign In Required
Please sign in to use Codespaces.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching GitHub Desktop
If nothing happens, download GitHub Desktop and try again.
Launching Xcode
If nothing happens, download Xcode and try again.
Launching Visual Studio Code
Your codespace will open once ready.
There was a problem preparing your codespace, please try again.
Latest commit
Git stats
Files
Failed to load latest commit information.
Latest commit message
Commit time
README.md
Алгоритмы. Вариант 38
pypy3 solver15.py in.dat out.ans
python3.5 solver15.py in.dat out.ans
python3.5 test_solver15.py
Some other tests:
python3.5 tests.py pypy3 tests.py #faster stronger harder better
Testing can take a long time (over 20 — 40 sec), be patient and have a tea.
Постройте программу для решения головоломки «Пятнашки» произвольного размера.
Игра представляет собой поле 4 на 4 (классический вариант), на котором расположены 15 фишек, пронумерованных числами от 1 до 15, а одно поле оставлено пустым. Требуется, передвигая на каждом шаге какую-либо фишку на свободную позицию, прийти в конце концов к следующей позиции:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 __
Доказательство NP полноты для кратчайшего решения пятнашек размерности n.
Проверка на существование решения
Пусть дана некоторая позиция a на доске:
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16
где один из элементов a[z] равен нулю и обозначает пустую клетку. Рассмотрим перестановку:
a[1]a[2]. a[z-1]a[z+1]. a[15]a[16]
(т.е. перестановка чисел, соответствующая позиции на доске, без нулевого элемента.
Обозначим через N количество инверсий в этой перестановке (т.е. количество таких элементов a[i] и a[j] , что i < j , но a[i] >a[j] ).
Далее, пусть K — номер строки, в которой находится пустой элемент (т.е. K = (z — 1) div n + 1 ).
Тогда, решение существует тогда и только тогда, когда:
Весь процесс поиска решения в «Пятнашках» можно представить как задачу поиска на графе. Вершинами такого графа будут состояния поля головоломки, полученные в результате перемещения костяшек.
Поиск решения можно свести к поиску терминального состояния игрового поля (обычно, в качестве терминальной, выбирается расстановка костяшек, упорядоченных по возрастанию слева направо, сверху вниз — 1,2,3. ).
Для решения задачи поиска терминальной вершины на графе, можно использовать алгоритмы полного перебора (поиск в глубину или ширину), но количество возможных решений (возможных перестановок) скорее всего окажется слишком большим (сложность в таком случае: О(n ^ 2 !)), где n — количество всех вершин графа (а для пятнашек размера 4х4 это уже 16! если отсекать циклы)
Возможные алгоритмы для решения:
- Поиск в ширину
- Поиск в глубину
- Алгоритм Флойда
- Алгоритм Форда-Беллмана
- Алгоритм Дейкстры
- Алгоритм A*
Все неинформированные методы поиска сразу отсекаются, т.к. перебор всех вершин займёт большее количество времени.
По той же причине можно убрать алгоритмы поиска пути от каждой вершины до каждой. И остается только А*.
Так же в статье с доказательством приводится описание полиномиально — приближенного алгоритма. По принципу работы он похож на А* — использует эвристическую оценку расстояния до терминальной вершины. Минусом является сложность понимания (86 страниц на английском) и реализации.
Алгоритм A* позволяет существенно сократить количество состояний для перебора, путем применения некоторой дополнительной информации — эвристики. В качестве такой информации для пятнашек я возьму несколько эвристик описанных ниже.
Алгоритм A* предполагает наличие двух списков вершин графа: открытого и закрытого. В первом находятся вершины, еще не проверенные алгоритмом, а во втором те вершины, которые уже встречались в ходе поиска решения.
На каждом новом шаге, из списка открытых вершин выбирается вершина с наименьшим весом (поэтому использовалась очередь). Вес (F) каждой вершины вычисляется как сумма расстояния от начальной вершины до текущей (G) и эвристическое предположение о расстоянии от текущей вершины, до терминальной (H).
Fi = Gi + Hi, где i — текущая вершина (состояние игрового поля).
Временная сложность алгоритма A* зависит от эвристики. В худшем случае, число вершин растёт экспоненциально по сравнению с длиной оптимального пути, но сложность становится полиномиальной, когда эвристика удовлетворяет следующему условию:
h(x) — h*(x)
где h* — точная оценка расстояния из вершины x к цели. Другими словами, ошибка h(x) не должна расти быстрее, чем логарифм от оптимальной эвристики.
В худшем случае алгоритму приходится помнить экспоненциальное количество узлов. Есть так же улучшенные по памяти версии алгоритма А*: IDA*, MA* и Recursive Best-First Search. Но для задачи решения пятнашек они будут потреблять сравнимое количество памяти за счёт использования рекурсии (400-500 Мб для размерности 4х4 на A*, против 300-350 Мб на IDA*). Так же для рекурсивных алгоритмов требуется доработка для контроля глубины рекурсии, иначе они потребляют гораздо больше памяти.
Все эвристики будут рассмотрены на примере пятнашек размерности 3, но так же являются верными и для размерности n.
После непродолжительного поиска, было принято решение взять за основу сумму следующих эвристик:
Функция: manh_distance()
Основная эвристика, это сумма расстояний по строкам и столбцам от текущего расположения костяшки до ее правильной позиции. Допустимость следует из того, что за один ход перемещается только одна фишка, и расстояние между этой фишкой и её конечной позицией изменяется на 1
| 6 | 5 | 4 |
| 7 | 8 |
this->manh_distance() // == 4
Функция: linear_conflict()
Костяшка I и костяшка J находятся в линейном конфликте по строке, если они обе стоят в своей строке, но костяшка I находится левее костяшки J, хотя на самом деле должна быть справа. Мы должны подвинуть одну из костяшек со строки, поэтому можем добавить 2 к общей эвристике. Аналогичным образом рассматривается линейный конфликт по столбцу. Правый нижний угол в эвристике не рассматривается, так как очень сложно скомбинировать этот случай с last_move.
| k | k | k |
| k | k | k |
this->manh_distance() // H + 2
Функция: corner_tiles()
Пусть на месте 1 стоит любая другая костяшка, а один из её соседей (или оба), уже выставлен на своё место, тогда чтобы поставить единицу на место соседей придётся подвинуть. Прибавляем 2 к общей эвристике. Если соседи уже участвуют в linear_conflict, то всё учтено и 2 добавлять уже не нужно.
| k | k | k |
| k | k | k |
| 4 | k | k |
| k | k | k |
this->corner_tiles() // == H + 2 в обоих случаях
Функция: last_move()
На последнем ходу у нас есть два варианта:
| 4 | 5 | 6 |
| 7 | 8 |
| 4 | 5 | |
| 7 | 8 | 6 |
this->last_move() // == H + 0 в обоих случаях, при другом расположении 6 и 8 прибавляем 2.
Если костяшки не находятся на требуемых позициях, манхэттенское расстояние не учитпроверка на сущестывает переход через угол. Следовательно, мы можем добавить к нему 2.
Оценка необходимости подбора оптимальных эвристик
Попробуем увидеть разницу в работе алгоритма с различным числом эвристик.
Все варианты тестировались так:
time pypy3 solver15
Со следующим набором входных данных:
5 1 9 3 11 13 6 8 14 10 4 15 0 12 7 2
Для начала просто посмотрим как долго алгоритм работает с простейшей эвристикой:
simple_heur() # число фишек стоящих не на своих местах time: >4m len(node_hash): max # алгоритм так и не закончил работу, # будем считать эвристику неоптимальной
Будем наращивать функцию h(x), начиная с h(x) = manhattan_distance().
Попробуем запустить алгоритм с одной лишь эвристикой manhattan_distance():
time: 1m23,330s len(node_hash): 696569 len(decision): 41
Длина списка вершин которые мы обошли просто огромна, т.к. большинство эвристик будут отличаться на слишком малую величину, алгоритму придётся обойти большое количество вершин прежде чем станет понятно где вершины с наименьшим весом.
Далее добавим простейшую (с малым весом) дополнительную эвристику last_move():
time: 36,829s len(node_hash): 283798 len(decision): 41
Увидим сокращение пройденных вершин в 2,5 раза и, само собой, такой же результат по длине решения. Сократили число рассматриваемых вершин, получили и сокращение времени. Это произошло из за большей дифференциации весов вершин. Алгоритм с большей вероятностью выбирает правильный путь.
Добавив эвристику corner_tiles() увидим следующее:
time: 1m49,561s len(node_hash): 192863 len(decision): 41
Количество рассматриваемых вершин уменьшилось, но время увеличилось. Это произошло из за сложности эвристической функции corner_tiles. Отсюда можно сделать вывод, что эвристическая функция должна быть не только близка к значение реального расстояния, но и быть довольно легковесной, т.к. применяться она будет к большому количеству вершин.
По той же причине была убрана эвристика linear_conflict(). Таким образом, итоговая эвристическая функция выглядит как:
h(x) = manhattan_distance() + last_move()
В файле a_star.py находится реализация основого алгоритма и краткое описание его работы.
В начале работы просматриваются узлы, смежные с начальным; выбирается тот из них, который имеет минимальное значение f(x), после чего этот узел раскрывается. На каждом этапе алгоритм оперирует с множеством путей из начальной точки до всех ещё не раскрытых (листовых) вершин графа — множеством частных решений, — которое размещается в очереди с приоритетом. Приоритет пути определяется по значению f(x) = g(x) + h(x). Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди, либо пока всё дерево не будет просмотрено. Из множества решений выбирается решение с наименьшей стоимостью.
Для сравнения эвристик для каждой цепочки решений использую очередь с приоритетами, для работы которой перегружаю оператор __lt__()
Для хранения списка пройденных вершин использую хэш таблицу или dict в python.
Имплементация самого решателя пятнашек находится в файле solver15.py .
Внутри определена функция для подсчёта Манхэттенского расстояния и класс chain15 содержащий конкретную реализацию представления пятнашек в виде графа. К каждой функции приведено описание или принцип работы ясен из её названия.
Файлы test_a_star.py , test_solver15.py , tests.py содержат тесты и примеры использования для алгоритма A*, класса перевода пятнашек в задачу на графе, программы решения пятнашек соответственно. Тесты описаны в формате docstring.
Формат входных и выходных данных
На вход первой подаём состояние поля, оно должно соответствовать разумному смыслу, т.к. никак не валидируется, пустой символ это 0:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
На выходе даст бог получим первой строкой число ходов до решения, а далее состоянии доски на каждый ход:
353 1 2 3 4 5 6 7 8 9 10 11 12 13 15 14 0 ———- 1 2 3 4 5 6 7 8 9 10 11 12 13 15 0 14 . . .
. либо: NO SOLUTION FOR YOUR COMBINATION
Что можно улучшить
- Эвристики (сложно, но можно найти в англоязычных статейках умные варианты)
- При равенстве функций f (эвристических расстояний) очередь с приоритетами работает как стек (LIFO), это зависит от реализации. Можно узнать как в конкретном случае (для пятнашек) это влияет на скорость нахождения решения. И, например, заменить реализацию очереди на свою — FIFO в случае равенства эвристик.
- Для случая из предыдущего пункта получаем: При LIFO — поиск в глубину, при FIFO — в ширину. В зависимости от величины эвристики можем подставлять ту или иную очередь. Тоесть чем меньше эвристика тем ближе мы к решению, тем выгоднее нам уходить вглубь. И наоборот, при большой величине эвристической функции интересно посмотреть в ширину, не уменьшается ли она там.
Можем из алгоритма A* получить Greedy Wide Algorithm убрав g() из:
f() = h() + g()
Тогда получим для следующих входных данных:
5 1 9 3 11 13 6 8 14 10 4 15 0 12 7 2
time: 1,641s len(node_hash): 2721 len(decision): 291
Заметим намного меньшее время по сравнению с предыдущими замерами на A star. Но так же и возросшую длину решения. Это произошло из за того что алгоритм следит лишь за весов следующей вершины — берёт минимальную. А сколько вершин было позади его уже не интересует.
Число рассмотренных вершин так же, меньше.
Можно сделать вывод что в случаях, когда необходимо получить любое решение и его длина не важна, выгоднее использовать такой вариант.
Полный A star в свою очередь находит оптимальное решение.
Посмотрим результаты работы профилировщика для жадного алгоритма (так как он работает быстрее):
python3.5 -m cProfile -s time solver15.py
Start from: 5 1 9 3 11 13 6 8 14 10 4 15 0 12 7 2 —— Result: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 —— 414 moves 92069971 function calls (92069970 primitive calls) in 53.480 seconds Ordered by: internal time ncalls tottime percall cumtime percall filename:lineno(function) 1796766 24.731 0.000 48.634 0.000 solver15.py:28(manh_dst) 28878926 20.555 0.000 24.051 0.000 solver15.py:6(manh_dst_matrix) 57757852 3.496 0.000 3.496 0.000 898383 0.789 0.000 50.037 0.000 solver15.py:65(__lt__) 39392 0.778 0.000 1.712 0.000 solver15.py:68(get_neighbours) 1796766 0.614 0.000 49.248 0.000 solver15.py:62(f) 118045 0.598 0.000 0.682 0.000 solver15.py:23(__init__) 1 0.553 0.553 53.391 53.391 a_star.py:11(a_star) 157437 0.480 0.000 0.480 0.000 solver15.py:35(last_node) 39393 0.363 0.000 30.647 0.001 75215 0.247 0.000 20.000 0.000 1 0.088 0.088 53.480 53.480 solver15.py:1() 118045 0.066 0.000 0.066 0.000 118043 0.051 0.000 0.051 0.000 39392 0.030 0.000 0.030 0.000 118043 0.022 0.000 0.022 0.000 118049 0.018 0.000 0.018 0.000
Видно, что большая часть нагрузки приходится на эвристическую функцию:
def manh_dst(self): dst = 0 for i in range(0, int(self.size ** 2)): dst += manh_dst_matrix((self.board_state[i] — 1) % (self.size ** 2), i, self.size) return int(dst)
Не помешает что нибудь улучшить:
- a*a быстрее чем a ** 2
- да и вообще зачем каждый раз считать квадрат, можно сделать отдельную переменную
Получаем время 41.259s с теми же данными, что +22% к скорости.
time python3.5 solver15.py
Без профилировщика: 27,313s
Выходит всё же долго (тот же алгоритм на C++ работает за 1,421s). Можем использовать оптимизированные сборки Python:
time pypy3 solver15.py
Получаем 4,128s. Что всего в 4 раза медленнее чем на С++.
Источник: github.com