Лабораторная работа по нахождению численных решений ОДУ тремя методами: Эйлера, Эйлера-Коши и Рунге-Кутты. В архиве представлена постановка задачи, блок схемы реализации методов, коды программ трёх методов на C++, а так же подведён итог проделанной работы.
Фрагменты из архива:
Постановка задачи:
Найти приближенное решение ОДУ y’= x^3 + y^3 при заданном начальном условии y(0) = 0 в трех узлах на отрезке [0,1] с шагом h = 0.3 методами Эйлера, Эйлера-Коши и Рунге – Кутты.
Код программ:
#include «stdafx.h»
#include
#include
#include
typedef double typeOfFloat;
typeOfFloat f( typeOfFloat x, typeOfFloat y );
typeOfFloat integral( typeOfFloat a, typeOfFloat b, typeOfFloat y, int n );
typeOfFloat integralOnPiece( typeOfFloat a, typeOfFloat b, typeOfFloat y, typeOfFloat E );
typeOfFloat a,b;
typeOfFloat h;
typeOfFloat e;
typeOfFloat y0;
using namespace std;
// Нахождение f(x,y)
Численное решение задачи Коши методом Эйлера
typeOfFloat f( typeOfFloat x, typeOfFloat y )
<
return ( x*x*x + y*y*y );
>
Для решения дифференциальных уравнений наиболее точным и быстрым является Метод Рунге-Кутты, который за малое число шагов дает наиболее точный результат. Однако, для понимания и при написании программы наиболее прост метод Эйлера. Метод Эйлера-Коши промежуточный метод между двумя другими, но в моём случае он показал наихудшую точность.
Похожие материалы:
- Complex Matrix
- Численные методы. Мудров А.Е
- ЛР №1 — Работа с Adobe Photoshop
- QT 4.3.1
- Организация многооконного интерфейса
Источник: fevt.ru
lab_4 / lab4_25
Точное аналитическое решение ДУ находится методом разделения переменных:
После интегрирования и преобразования данного выражения получаем:
Подставим и в выражение, чтобы найти :
Аналитическое решение дифференциального уравнения:
Значения точного решения ОДУ —
Вычислим в сценарии Scilab значения полученного решения на отрезке с шагом изменения аргумента : 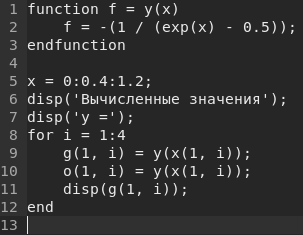

Численное решение заданного ОДУ методом Эйлера
Вычислим в сценарии Scilab значения численного решения ОДУ методом Эйлера — — в точках отрезка с шагом . Для этого метода ОДУ записывают в виде . Общая формула для определения очередного значения функции по методу Эйлера имеет вид , где . 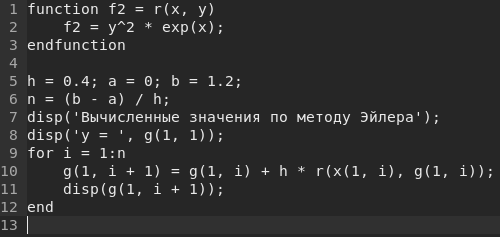

Погрешность метода Эйлера
Решение ОДУ методом Эйлера (программа)
Вычислим в сценарии значения погрешностей , где : 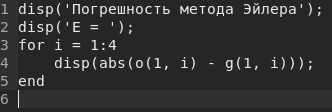

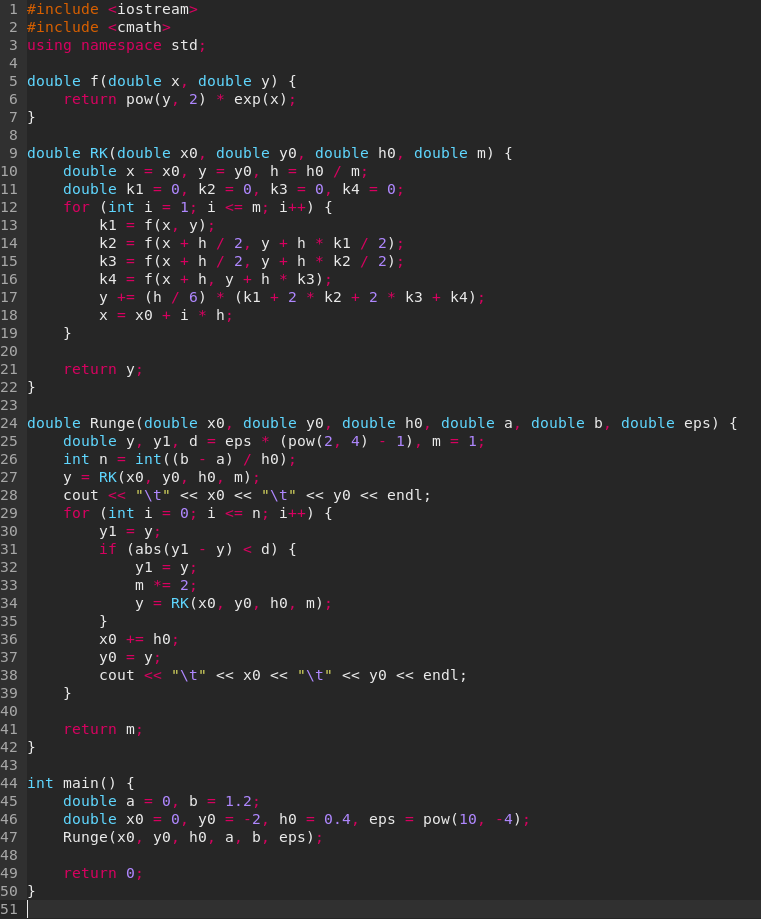
Решение ОДУ методом Рунге-Кутта 4-го порядка, дополненным методом автоматического выбора шага, обеспечивающим точность
Вычислим в программе значения численного решения ОДУ с точностью и получим решение в точках отрезка с шагом — — методом Рунге-Кутта 4-го порядка, используя формулу: , где
Схема алгоритма приведена в разделе 2.5 пособия по алгоритмам.
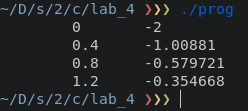
Значения погрешностей
Вычислим в сценарии Scilab значения погрешностей: 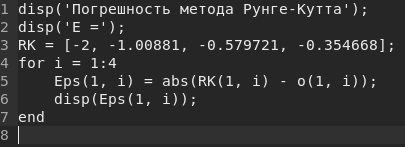

Решение ОДУ средствами пакета Scilab

Решим ОДУ, используя функцию ode():
Сведём полученные значения в таблицу:
Источник: studfile.net
Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.
Обыкновенные дифференциальные уравнения
- Задача Коши
- Краевая задача
- Задача на собственные значения
Кратко расскажу о их сути:
Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.
Методы решения дифференциальных уравнений
Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.
В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.
Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.
Метод Рунге-Кутта первого порядка
Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.
Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:
Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).
Setka=10:10:10000; for k=1:length(Setka) %определяем параметры сетки N=Setka(k); h=1.0/(N-1); %задаем начальное условие y(1)=1; %применяем алгоритм метода ломаных/Эйлера for n=1:(N-1) y(n+1)=y(n)+ h*((n-1)*h*y(n)); %где (n-1)*h -> x end %вычисляем величину M(1) в оценке %погрешности численного решения M(k)=abs(y(N)-exp(0.5))/h; step(k)=h; end %рисуем зависимость величины M(1) от шага plot(step,M);

На данном графике показана зависимость величины ошибки от шага.
Метод Рунге-Кутта второго порядка
Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение.
Это позволяет поднять порядок скорости сходимости до двух.
Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.