Наиболее общим подходом к решению нелинейных задач является разбитие процесса возведения системы на этапы.
На каждом из этапов возведения выполняются работы по установке (удалению) отдельных конструктивных элементов или их групп, регулированию фактических размеров элементов несущих конструкций, введению (удалению) временных связей, изменению параметров связей системы с внешней системы и т.п., изменяются жесткостые параметры элементов модели и связей и др.
В основу технологий расчёта, учитывающих указанные выше обстоятельства, положен принцип поэтапного отслеживания изменения основных параметров расчётной модели (геометрии, жесткостных параметров элементов модели и связей, нагружения и деформирования) с замыканием системы на каждом (заранее определённом этапе возведения здания.
При этом различают суммарное НДС системы, возникающее на каждом этапе монтажа с учётом всех предшествубющих этапов, и приращение НДС, вызванное дополнительными воздействиями на систему, относящимися исключительно к рассматриваемому этапу монтажа.
Быстрое решение нелинейных статических задач в SCAD++
При этом для каждой стадии монтажа все расчёты выполняются в преположении справедливости допущений линейной строительной механики, а, в целом, задача становится нелинейной за счёт изменения расчётной схемы при переходе от одного этапа к другому.
Простой шаговый метод расчёта нелинейно упругих систем:
(как правило, применяется для решения задач физической и геометрической нелинейности)
Шаговый метод заключается в том, что нелинейно упругую систему нагружают постепенно, малыми порциями нагрузок ΔP, каждый раз получая малые приращения деформаций, внутренних сил и перемещений.
На этих малых перемещениях с достаточной точностью считают, что система ведёт себя как линейно-упругая с коэффициентами упругости, зависящими от достигнутого уровня напряжений в элементах системы.
На первом этапе расчёт на нагрузку ΔP ведётся как для обычной линейно упругой системы.
Таким образом на каждом шаге решается линеаризованная задача (система уравнений для текущего приращения вектора узловых нагрузок, сформированного для конкретного нагружения), и, в предположении, что это решение является достаточно точным, реализуется переход к следующему шагу нагружения.
Далее деформации, полученные от второго этапа нагружения суммируют с деформациями, полученными от первого этапа и т.д.
Точность расчёта шаговым методом зависит от количества шагов (размера шагов нагружения) (величина шага).
Погрешность решения нелинейной задачи, обычно, не контролируется, количество шагов задается пользователем или автоматически.
При недостаточном количестве шагов замена бесконечно малых шагов конечными может оказаться слишком грубой.
При очень малых шагах (большом их количестве) может быть уменьшена точность вычислений.
Особенно чувствительными к величине шага являются геометрически нелинейные задачи.
Алгоритм решения задач с геометрической нелинейностью:
ПК ЛИРА 10 в задачах. Тема 20. Геометрическая нелинейность
1 Создание расчётной схемы
— задание исходных данных (геометрия, граничные условия, нагрузки, жесткостные параметры)
— задание КЭ (конечных элементов), учитывающих геометрическую нелинейность
2 Моделирование нелинейных загружений
Процесс деформирования конструкции разбивается на шаги. Например, в программных комплексах, путем задания количества шагов.
3 Расчёт
На каждом шаге для элементов вычисляются усилия (напряжения), а для узлов — перемещения
4 Анализ
При расчёте конструкций важно найти для каждого сечения элемента те сочетания отдельных загружений, которые могут быть наиболее опасными
Алгоритм решения задач с физической нелинейностью:
Для решения физически нелинейных задач шаговым методом необходимо задавать информацию о количестве шагов и коэффициентах к нагрузке. Схема может содержать несколько загружений, из которых допускается формировать последовательность (историю) нагружений.
Моделирование физической нелинейности (нелинейной упругости) материалов конструкций производится с помощью физически нелинейных конечных элементов.
Физически нелинейные конечные элементы воспринимают информацию из библиотеки законов деформирования материалов (зависимостей напряжения-деформации)
Методы расчёта нелинейных систем в ПК Лира 10 (Лира-Софт):
Нелинейный процессор реализует несколько методов для решения нелинейных задач различных типов:
— Шаговый метод
(описание данного метода см. выше)
(как правило, применяется для решения задач физической и геометрической нелинейности)
— Метод секущих (метод Биргера)
(как правило, применяется для решения физически нелинейных задач в режиме «инженерная нелинейность»)
— Итерационный метод (упрощенный метод Ньютона)
(применяется для решения задач конструктивной нелинейности (односторонние связи) и грунтовых массивов)
Моделирование физической нелинейности материалов конструкций производится с помощью специальных физически нелинейных конечных элементов, для которых реализована нелинейная зависимость напряжения-деформации.
Библиотека законов деформирования позволяет учесть практически любые нелинейные свойства материала и её можно пополнять.
Физически нелинейные расчёты лучше производить с итерационными элементами (для стержней — КЭ тип 510). Итерационные элементы дают намного лучшую сходимость и более сглаженные результаты, чем шаговые элементы (для стержней имеются ввиду КЭ типов 210, 410).
Шаговые элементы лучше использовать в самых крайних случаях или при решении геометрически нелинейных задач, когда без них вообще не обойтись.
Нелинейный процессор позволяет получить напряженно-деформированное состояние с учётом нелинейных эффектов как для мономатериальных, так и для биматериальных конструкций.
Для последних предлагается определенный набор характеристик второго материала (армирующих включений).
Методы расчёта нелинейных систем в SCAD:
Решение нелинейных задач реализовано в нескольких модификациях шагового метода:
— Простой шаговый метод
(описание данного метода см. выше)
— Шаговый с уточнениями
Данный вариант предусматривает контроль невязок на каждом шаге и итерационное уточнение нагружения очередного шага за счет учёта невязки в уравнениях равновесия. При этом итерации выполняются с неизменным значением линеаризованной матрицы жесткости, которая была вычислена в начале очередного шага.
— Шагово-итерационный
В данном случае производится итерационное уточнение решения на каждом шаге с корректировкой линеаризованной матрицы жесткости на каждой итерации.
В ПК Лира-САПР
В Лира-САПР реализована шаговая (применяется для геометрически и физически нелинейных задач) и итерационная (для решения задач с конструктивной нелинейностью) нелинейность
В САПФИР 2021 от ПК Лира-САПР можно создавать расчётные схемы для проведения расчётов с учётом физической нелинейности.
Для этого в свойствах объектов задаются требуемые типы конечных элементов и назначается нелинейный материал.
(Выбирается опция «наделить нелинейными свойствами», а в свойствах конструкции корректируется параметр «жесткость» и задается, например КЭ 244/241 — физически нелинейный универсальный КЭ оболочки)
Далее для нелинейного материала следует выбрать (создать) закон нелинейного деформирования и построить диаграмму поведения материалов напряжения-деформации. Данную операцию нужно выполнять для основного и армирующего материалов.
В библиотеке законов деформирования материалов Лира-САПР существуют кусочно-линейный (14) и экспотенциальные законы деформирования (11,21,31,15,25,35).
В справочнике Лира-САПР 2021 содержатся данные для заполнения закона деформирования армирующего материала. Чтобы задать армирование конструкции, которое будет учтено в расчёте, можно создать модель армирования в САПФИР — в программе можно выполнить раскладку арматуры, которая будет передана в Визор как заданное армирование.
Далее в САПФИР 2021 существует возможность задания истории нагружения, чтобы нагрузки прикладывались в определённой последовательности и учитывалась генетическая нелинейность. Историй нагружения может быть несколько
*До начала формирования истории нагружения, к конструкции уже должны быть приложены все нагрузки и распределены по нагружениям. В свойствах конструкции можно выбрать загружение, в котором будет приложен собственный вес.
Для вызова диалогового окна создания монтажных стадий в САПФИР, следует нажать на соответствующую кнопку на панели инструментов. Если в этом окне нажать кнопку «Авто», программа сформирует монтажные стадии на основании структуры проекта — столько стадий, сколько задано этажей.
Как правило, одна стадия соответствует одному этажу. На каждой стадии происходит монтаж или демонтаж каких-то объектов — это могут быть конструкции или нагрузки. В каждую стадию входят два события — монтаж конструкций и нагрузок.
Для каждого нового события определяется, что будет происходить — демонтаж или демонтаж, в какой момент времени это произойдёт (после какой стадии).
Источники для более глубокого изучения вопроса:
А.В. Перельмутер — Беседы о строительной механике — 2016 г
Источник: porebrick.blogspot.com
Инженерная и физическая нелинейность
Смысл расчета инженерной нелинейности в автоматическом определении новых жесткостей заармированного и нагруженного сечения.
Для этого поперечное сечение элемента разбивается на элементарные площадки (для стержня, а для пластины на слои). Процессор вычисляет усилия от «определяющей комбинации», подбирает арматуру и пересчитывает жесткость сечения: в каждой элементарной площадке бетона и точечном включении арматуры находится новая «секущая» жесткость (в зависимости от того, в какую точку диаграммы мы попали). Если открывается трещина, то элементарные площадки бетона, которые в неё попали из расчета жесткости сечения исключаются.
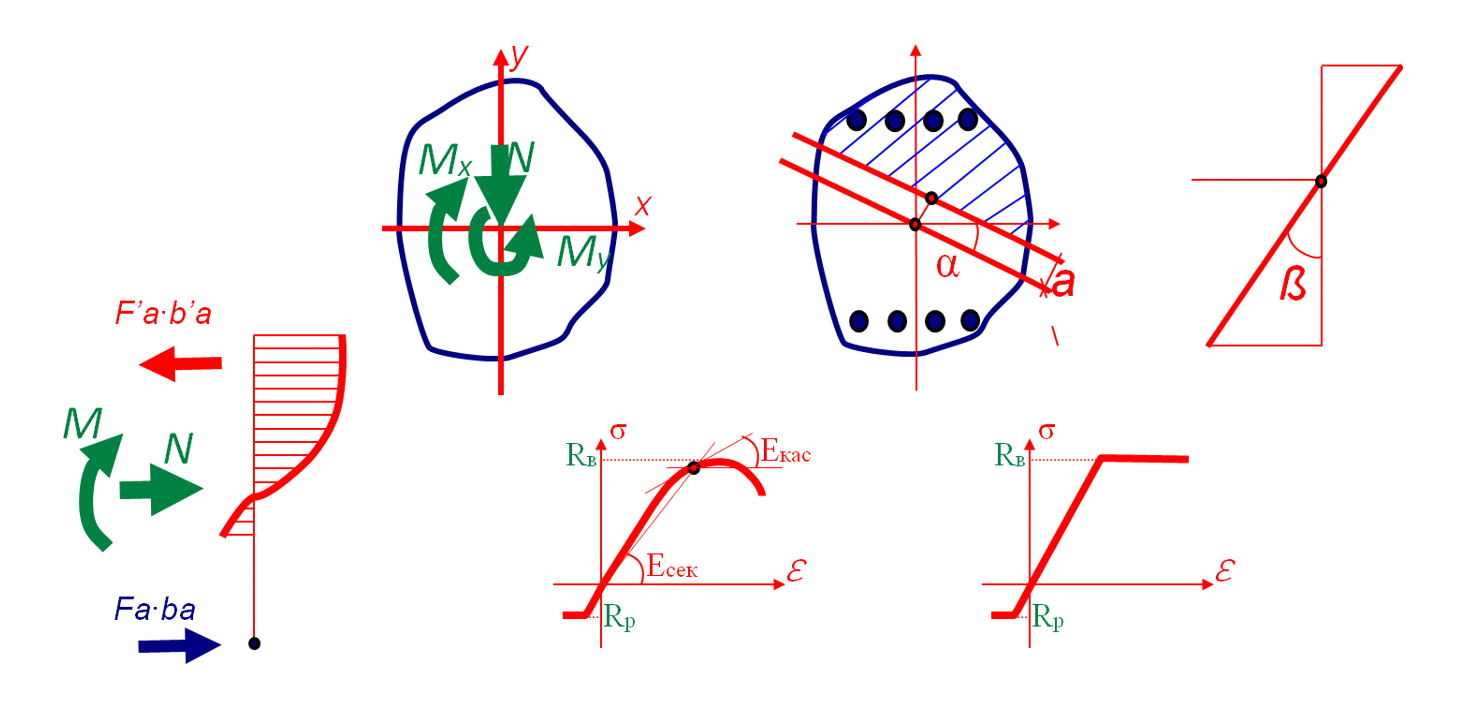
Определение жесткостей сечения железобетонного стержня
Расчет железобетонных конструкций в нелинейной постановке
Сравнительный анализ объемов исходных данных для инженерной нелинейности и шагового нелинейного расчета: синим цветом что требуется от пользователя, черным – делает процессор
| Расчет на эксплуатационные нагрузки (метод секущих) | Компьютерное моделирование процесса нагруженния (шаговый метод) |
| 1. Составления определяющего нагружения (1 параметрическая таблица) | 1. Задание нелинейных материалов |
| 2. Расчет на определяющее нагружение | 2. Расстановка армирования во всех нелинейных элементах |
| 3. Итерационный расчет (подбор армирования/уточнение жесткостей), в итоге — определение секущих жесткостей | 3. Формирование истории нагружения |
| 4. Расчет на эксплуатационные нагрузки | 4. Расчет на I-м шаге с жесткостью E0 на нагрузки P/n (n — к-во шагов) |
| 5. Определения РСУ и РСН | 5. Расчет на II-м шаге с жесткостями с соотв. изменениями полученными на I-м шаге |
| 6. Конструирование (подбор армирования по усилиям от матрицы с переменными жесткостями) | 6. Расчет на m шаге по касательным жестокостям соответсвующим усилиям получаемых на m-1 шаге Nm-1=△N1+△N2+. +△Nm-1 Um-1=△U1+△U2+. +△Um-1 |
Расчет по инженерной нелинейности отличается от линейного расчета только заданием одной таблицы, которая формирует определяющую комбинацию нагрузок
Сравнение результатов расчета линейного и инженерной нелинейности
а — линейный расчет
б — нелинейный расчет (инженерная нелинейность)
Источник: liraserv.com
Модули Физическая и Геометрическая нелинейность. Складское здание
В качестве практического задания было рассмотрено складское здание с этажеркой.

Рис.1.1.1. Общий вид здания
В качестве практического задания было рассмотрено складское здание с этажеркой. Здание складского типа, одноэтажное. Размеры по осям 17.700х42.750м. Высота до низа несущих конструкций покрытия – 11.900м.
Вертикальные несущие конструкции – железобетонные колонны с металлическими надколонниками из сварных двутавров. Несущие конструкции покрытия – стальные фермы с поясами из широкополочных двутавров и решеткой из профильной трубы. Геометрическая неизменяемость каркаса в плоскости рам обеспечивается самой рамой каркаса, из плоскости рам и по покрытию – распорками и диагональными связями. На отм. +4.500 между осями 6-7 располагается этажерка из железобетона.
Задача: смоделировать здание, выполнить расчет в линейной постановке, выполнить сравнительный расчет отдельных элементов с учетом нелинейности.
Построим модель здания и назначим сечения элементов:

Рис.1.1.2. Принятые сечения элементов каркаса
Назначим материалы для элементов:

Рис.1.1.3. Материалы
Назначим линейные загружения и сочетания нагрузок:

Рис.1.1.4. Загружения и сочетания
Произведем линейный расчет:

Рис.1.1.5. Деформированная схема при основном сочетании

Рис.1.1.6. Пример усилий в стержнях

Рис.1.1.7. Пример усилий в пластинах
Геометрическая нелинейность
Для проверки работы данного модуля создадим новый файл с пометкой «нелинейность». В загружениях оставим только те нагрузки, которые имеют ненулевую долю длительности. Список загружений:

Рис.1.1.8. Нелинейные загружения
Зададим автоматический выбор шага для каждого загружения:

Рис.1.1.9. Шаги нелинейного загружения
Анализировать будем перемещения стальной фермы по оси 5.

Рис.1.1.10. Схема фермы
Разобьем элементы фермы на большее количество частей, нежели в линейном расчете – 6-7 и более. Назначим элементам фермы тип конечного элемента – 310 КЭ, универсальный геометрически нелинейный стержень.

Рис.1.1.11. Тип конечного элемента
В файле с линейным расчетом создадим аналогичное РСН для сравнения:

Рис.1.1.12. Сравнительное РСН линейной задачи
Получим результаты. Линейная задача – перемещения от РСН по Z:

Рис.1.1.13. Перемещения по Z. Линейная задача
Нелинейная задача – перемещения по Z:

Рис.1.1.14. Перемещения по Z. Нелинейная задача
Как видно по схемам, перемещения отличаются, но отличия незначительные. Однако, они есть. Таким образом, при анализе более гибких систем (тросы, оттяжки, мачты) или же систем с большей нагрузкой неиспользование данного модуля может существенно сказаться на результатах задачи.
Для примера увеличим нагрузку от собственного веса металлоконструкций в 10р в линейной и нелинейной задачах. Получим результаты:

Рис.1.1.15. Перемещения по Z c увеличением нагрузки в нелинейной постановке

Рис.1.1.16. Перемещения по Z c увеличением нагрузки в линейной постановке
Соотношение перемещений 27.406/27.339=1,002 раза в первом случае
Соотношение перемещений 55.204/54.946=1.005 раза во втором случае
Физическая нелинейность
Для исследования работы физически нелинейных элементов рассмотрим безбалочную плиту перекрытия складского здания. Произведем смену конечного элемента пластин плиты. Назначим тип элемента 442.

Рис.1.1.17. Типы конечных элементов плиты
Назначим нелинейный материал для элементов плиты.

Рис.1.1.18. Нелинейный материал бетона

Рис.1.1.19. Нелинейный материал арматуры
Изменим сечение ж/б плиты так, чтобы оно соответствовало нелинейному расчету. Пусть плита заармирована по усилиям из линейного расчета и полученный диаметр арматуры — 20мм. Арматура в сечении располагается с шагом 200мм, т.о. площадь арматуры данного диаметра на 1м составит 15.7см2/м (5 стержней). Тогда на миллиметр условной сетки – 0.0157см2/мм.

Рис.1.1.20. Назначение сечения для нелинейного расчета
Историю загружений примем из расчета по рассмотрению геометрической нелинейности:

Рис.1.1.21. Нелинейные загружения
Для сравнения линейного и нелинейного расчетов рассмотрим деформации плиты по оси Z.

Рис.1.1.22. Перемещения в линейной постановке

Рис.1.1.23. Перемещения нелинейной постановке
Для сравнения также приведем мозайки усилий, чтобы показать их распределения по плите.
Как видно характер распределения имеет несколько иной характер.
Нелинейный расчет

Рис.1.1.24. Му. Нелинейный расчет

Рис.1.1.25. Му. Линейный расчет
Таким образом можно сказать, что применение физически нелинейного расчета показывает иной, реальный характер работы конструкции. За счёт перераспределений усилий в теле плиты перемещения выросли в 1.7 раза, что может существенно повлиять на подбор арматуры по 2-му предельному состоянию относительно линейной задачи.
Заметки эксперта
Новости
Публикации
Вебинары
Выгодные условия на приобретение российского ПО: nanoCAD, Renga, Pilot-BIM и др.
05 апреля 2023
Рассмотрим реальные примеры уже построенных или проектируемых объектов
22 марта 2023
Темы конференции: Геологические условия. Высотное строительство. Современные технологии и методы обеспечения качества и безопасности объектов.
03 февраля 2023
с 31 декабря по 8 января наш офис будет на каникулах
30 декабря 2022
В большинстве опытов по испытанию адгезионных соединений измеряется средняя адгезионная прочность. Данная величина вычисляется как отношение разрушающей нагрузки к площади склейки. Подобный подход подразумевает равномерное распределение касательных напряжений.
Исследователи давно обнаружили, что средняя адгезионная прочность соединения является сильной функцией геометрических [1] и физико-механических параметров модели и, следовательно, делает малоинформативными и несопоставимыми экспериментальные данные, выполненные на отличающихся образцах. Малочисленные результаты по измерению касательных напряжений по площади склейки с использованием преимущественно поляризационно-оптических методов [2] показывают, что распределение напряжений является нелинейной функцией. При этом наблюдается концентрация напряжений у торцов модели. В связи с этими фактами возникает необходимость детального изучения напряженно-деформированного состояния адгезионных соединений.
06 июня 2019
В статье рассмотрено практическое применение методики нелинейного статического анализа сейсмостойкости зданий и сооружений. Произведен расчет одноэтажной стальной рамы нелинейным статическим и нелинейным динамическим методами. В результате анализа полученных результатов расчета показана значимость высших форм колебаний и необходимость анализа их влияния на реакцию системы.
06 февраля 2018
С помощью современного программно-вычислительного комплекса ЛИРА 10.6 выполнена сравнительная оценка напряженно–деформированного состояния не поврежденного и коррозионно-поврежденного железобетонного элемента при динамическом и статическом нагружении. Проанализировано влияния ослабленного коррозией бетонного участка сжатой зоны на перераспределение напряжений в сечении.
25 января 2018
В статье рассматривается методика совместной работы ПК ЛИРА 10.6 и PLAXIS 3D посредством API модуля. С позиции инженера-расчетчика рассматриваются возможности передачи моделей между различными программами с применением технологий информационного моделирования.
Источник: lira-soft.com