Решение квадратного уравнения блок схема программа

Содержание

Понятие алгоритма. Изображение алгоритма в виде блок-схемы.

Алгоритмы линейной и разветвляющейся структуры

1.1. Понятие алгоритма

Алгоритм — четкое описание последовательности действий, которые необходимо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результаты, т.к. для решения любой задачи необходимо:

  1. Ввести исходные данные.
  2. Преобразовать исходные данные в результаты (выходные данные).
  3. Вывести результаты.
  • на естественном языке;
  • в виде блок-схемы;
  • в виде R-схемы.

Рассмотрим пример алгоритма на естественном языке:

  1. Ввести в компьютер числовые значения переменных а, b и с.
  2. Вычислить d по формуле d = b 2 — 4ас.
  3. Если d 1 и x 2.
  4. Прекратить вычисления.

1.2. Изображение алгоритма в виде блок-схемы

Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур — блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются следующими геометрическими фигурами:

Программа для решения корней квадратного уравнения с использованием дискриминанта на языке Паскаль


Блок начала-конца алгоритма (рис. 1.1). Надпись на блоке: «начало» («конец»).
Блок ввода-вывода данных (рис. 1.2). Надпись на блоке: слово «ввод» («вывод» или «печать») и список вводимых (выводимых) переменных.

Рис. 1.1. Блок начала-конца алгоритма Рис. 1.2. Блок ввода-вывода данных

Блок решения или арифметический (рис. 1.3). Надпись на блоке: операция или группа операций.
Условный блок (рис. 1.4). Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви «+», если условие не выполняется, то выполняется этап по ветви «–».

Рис. 1.3. Арифметический блок Рис. 1.4. Условный блок

В качестве примера рассмотрим блок-схему алгоритма решения уравнения (рис. 1.5), описанного в предыдущем подразделе.

Рис. 1.5. Блок-схема алгоритма решения квадратного уравнения

1.3. Алгоритмы линейной структуры

Линейный алгоритм — это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.6).

Рис. 1.6 Размещение блоков в линейном алгоритме

0.Блок схема. 8 класс

Рассмотрим несколько примеров линейных алгоритмов.

ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.

Пусть a, b, c — длины сторон треугольника. Необходимо найти S — площадь треугольника, P — периметр.

Для нахождения площади можно воспользоваться формулой Герона: где r — полупериметр.

Входные данные: a, b, c.
Выходные данные: S, P.

Блок-схема алгоритма представлена на рис. 1.7.

Рис. 1.7. Алгоритм примера 1.1

Внимание. В этих блоках знак » clear: both»>

Рис. 1.8. Алгоритм примера 1.2

ПРИМЕР 1.3. Заданы длины двух катетов в прямоугольном треугольнике. Найти длину гипотенузы, площадь треугольника и величину его углов.

Входные данные: a, b — длины катетов.
Выходные данные: с — длина гипотенузы, S — площадь треугольника, ?, ? — углы.

Блок-схема представлена на рис.1.9.

Рис. 1.9 Алгоритм примера 1.3

1.4. Алгоритмы разветвленной структуры

Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 1.10 — 1.11.

Читайте также:
Структура программы на языке программирования
Рис. 1.10 Фрагмент алгоритма Рис. 1.11 Пример разветвления

Рассмотрим несколько примеров построения алгоритмов разветвленной структуры.

ПРИМЕР 1.4. Известны коэффициенты и с квадратного уравнения. Вычислить корни квадратного уравнения.

Входные данные: a, b, c.
Выходные данные: x 1 , x 2 .

Блок-схема представлена на рис. 1.5.

ПРИМЕР 1.5. Составить программу нахождения действительных и комплексных корней квадратного уравнения. Можно выделить следующие этапы решения задачи:

  1. Ввод коэффициентов квадратного уравнения a, b и c.
  2. Вычисление дискриминанта d по формуле d = b 2 — 4ас.
  3. Проверка знака дискриминанта. Если d >= 0, то вычисление действительных корней по формуле 1.1 и вывод их на экран.
    (1.1)

Один из методов решения квадратных уравнений

Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения: Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи. После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.

procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin

х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);

Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.

  1. ввод коэффициентов исходного уравнения a, b, c;
  2. расчет дискриминанта d=b 2 — 4ac;
  3. анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
  4. вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.

Составить блок схему алгоритма решения квадратного уравнения

Свежие записи

  • Сера — химические свойства, получение, соединения.
  • Нитрат кальция: способы получения и химические свойства
  • Кальций: способы получения и химические свойства
  • Гидроксид натрия: способы получения и химические свойства
  • Гидроксид кальция: способы получения и химические свойства

Источник: al-shell.ru

LR1_BL_SH_Visio_set

MS Visio 2007 помогает преобразовать различные концепции в визуальную форму. MS Visio 2007 относится к классу программ — CASE-средств (Computer Aided Software/System Engineering), позволяющих проектировать любые системы на компьютере. Как необходимый элемент системного и структурно-функционального анализа, CASE-средства позволяют моделировать бизнес-процессы, базы данных, компоненты программного обеспечения, деятельность и структуру организаций и т.д.

Основное средство представления данных в MS Visio 2007 — это векторные фигуры. Для удобства фигуры сгруппированы по тематическим категориям, в каждой из которых можно увидеть похожие по внешнему виду или по теме элементы. Фигуры отображаются на одноименной области задач. Чтобы загрузить на нее фигуры определенной категории, нужно выбрать ее в меню «Файл>Фигуры».

На области задач может присутствовать несколько категорий одновременно, та из них, которая является активной, разворачивается, чтобы можно было увидеть фигуры, а остальные сворачиваются для экономии рабочего пространства. Для каждой фигуры можно увидеть ее название и графическое отображение.

Очень удобным способом работы с MS Visio 2007 является создание документа на основе шаблона. При загрузке шаблона на область задач «Фигуры» подгружаются те категории графических элементов, которые могут вам понадобиться в процессе работы. Для добавления фигуры в проект нужно просто перетащить ее на рабочую область, после чего можно откорректировать ее размеры, задать свойства и параметры отображения.

Читайте также:
Список литературы для 10 класса по программе зинина

Фигуры являются основным, но не единственным средством для представления данных в MS Visio 2007. Кроме них можно также использовать текст и числовые данные, графические элементы, форматирование цветом и т.д. При необходимости можно посетить веб-узел Microsoft (http://office.microsoft.com/ru-ru/visio/FX100487861049.aspx), чтобы получить о MS Visio 2007 более подробную информацию:

  1. Открыть MS Visio 2007. Откроется окно редактора «Приступая к работе»:

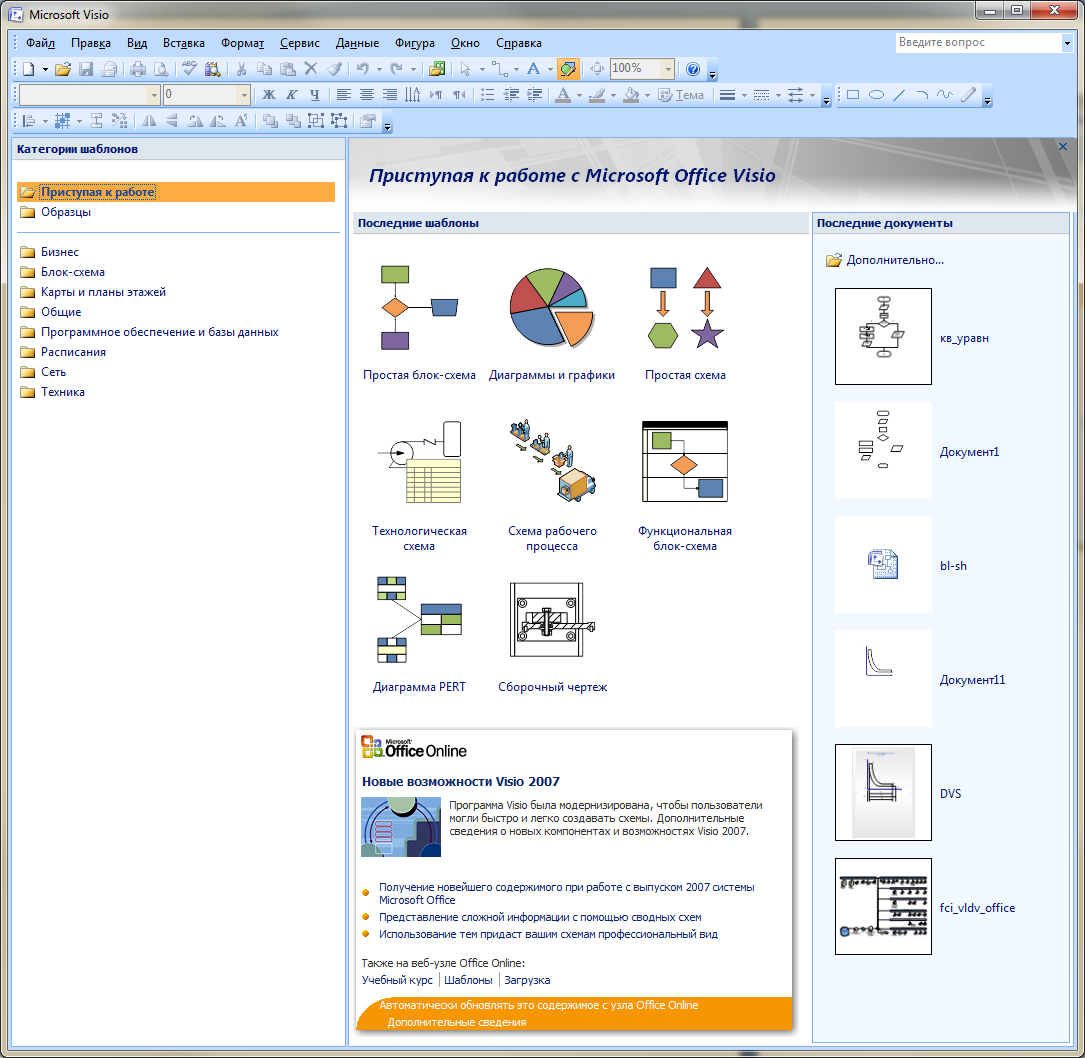
  1. При изучении основ алгоритмизации для создания схем алгоритмов чаще всего используется категория «Блок -схема».

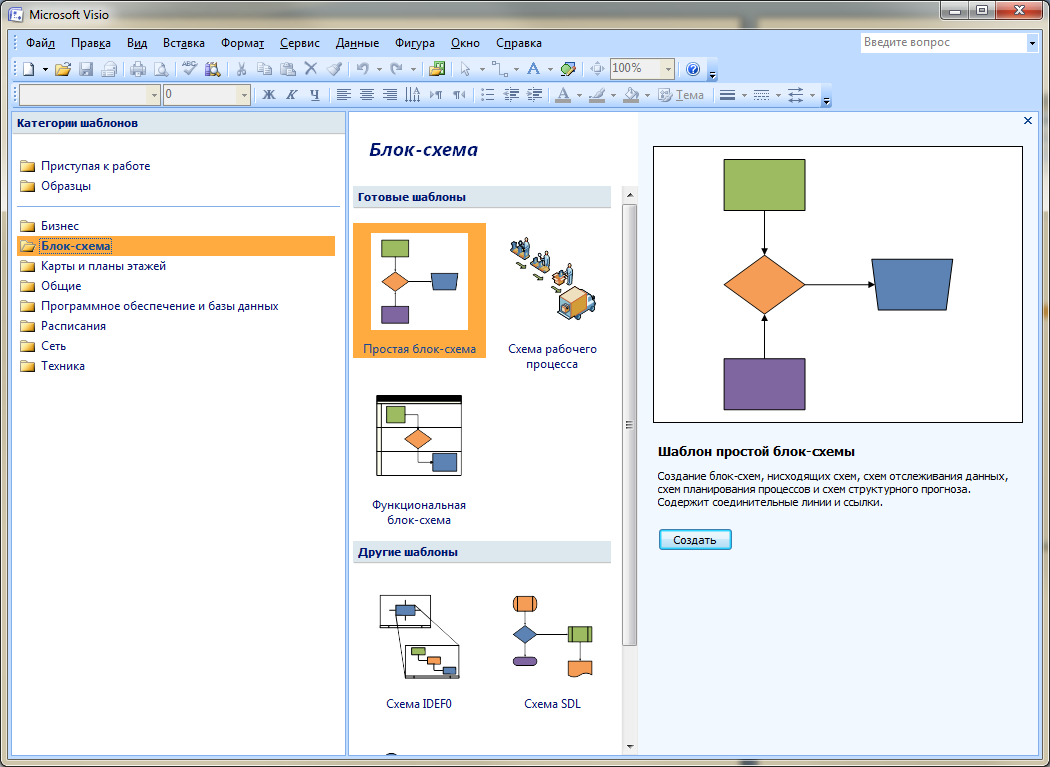
  1. Для начала работы необходимо выбрать шаблон «Простая блок-схема» и нажать кнопку Создать.
  2. Основной набор, который будет использоваться при создании блок-схемы, — «Фигуры простой блок-схемы». При необходимости загрузить фигуры данной категории, нужно выбрать ее в меню «Файл» и «Фигуры».

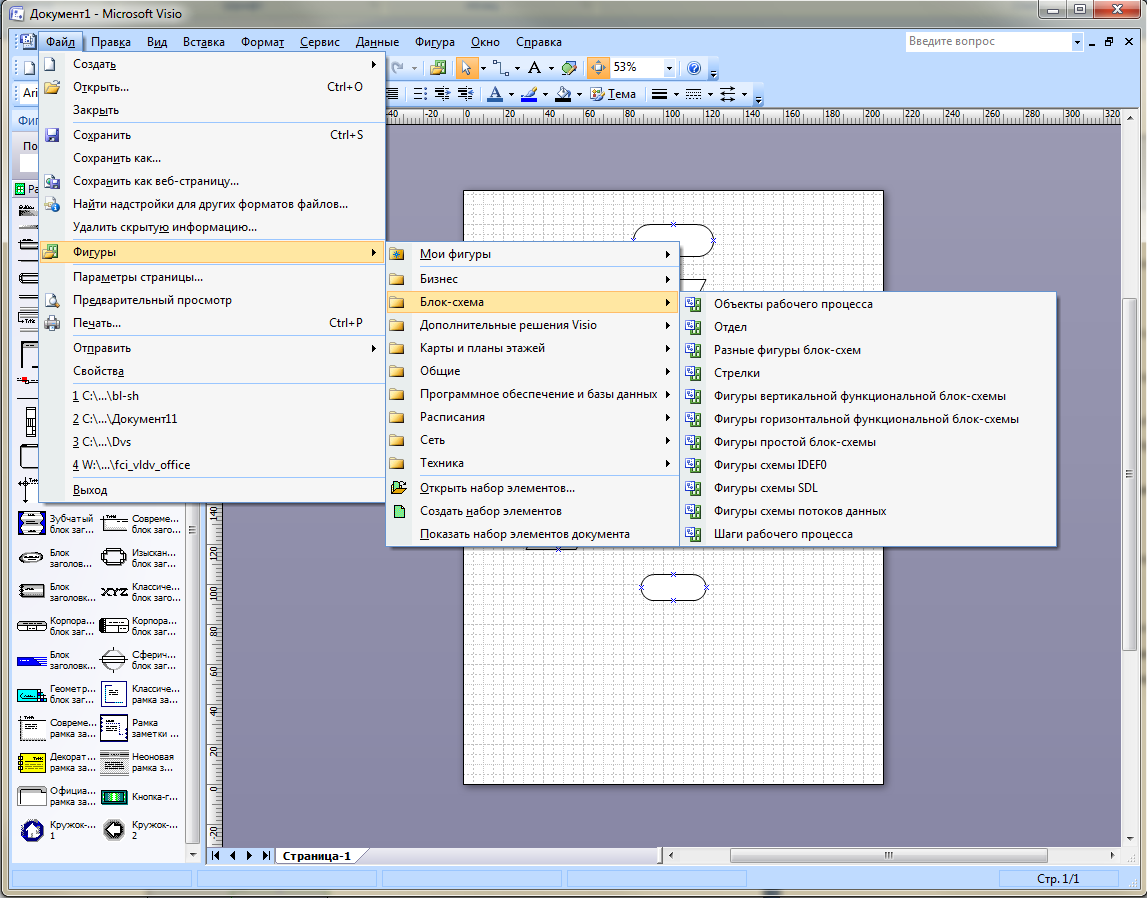
  1. Рабочая область пустого документа перед началом работы должна иметь следующий вид:

  1. Для нахождения корней квадратного уравнения вида ax 2 +bx+c=0 необходимо найти величины d, x1, x2 по следующим формулам:
№ Величина Формула
1 Дискриминант D D = b 2 -4ac
2 Корень x1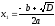
3 Корень x2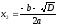
Если D > 0, уравнение имеет корни x1 и x2; Если D = 0, уравнение имеет корни, причем x1 = x2; Если D < 0, уравнение не имеет решения.
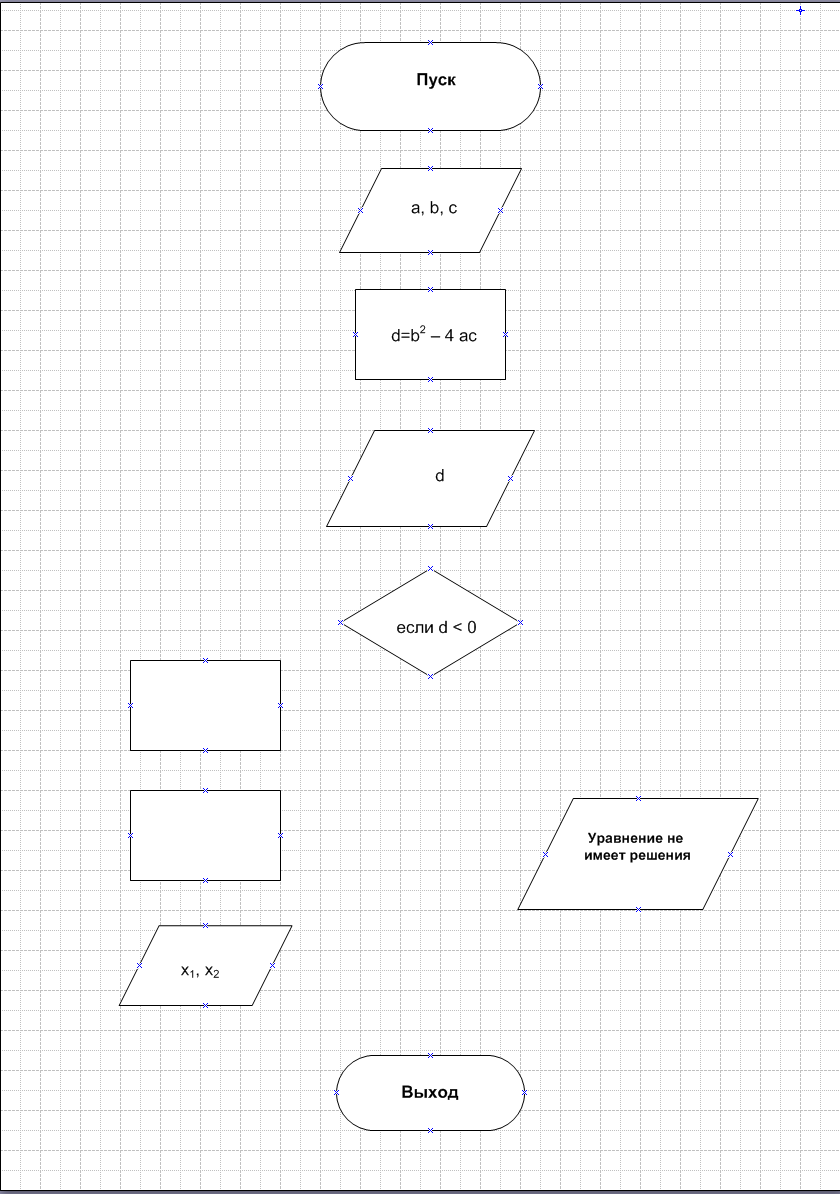
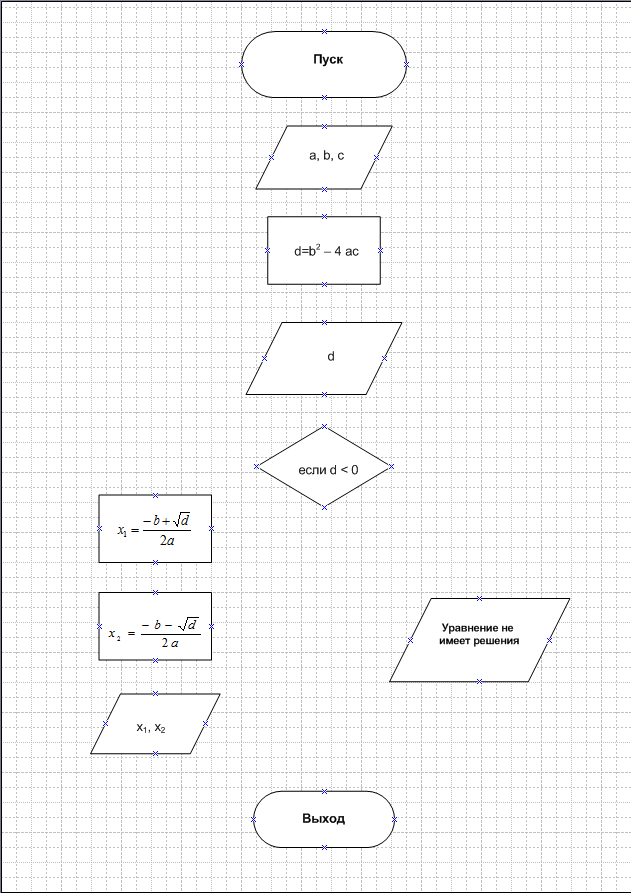
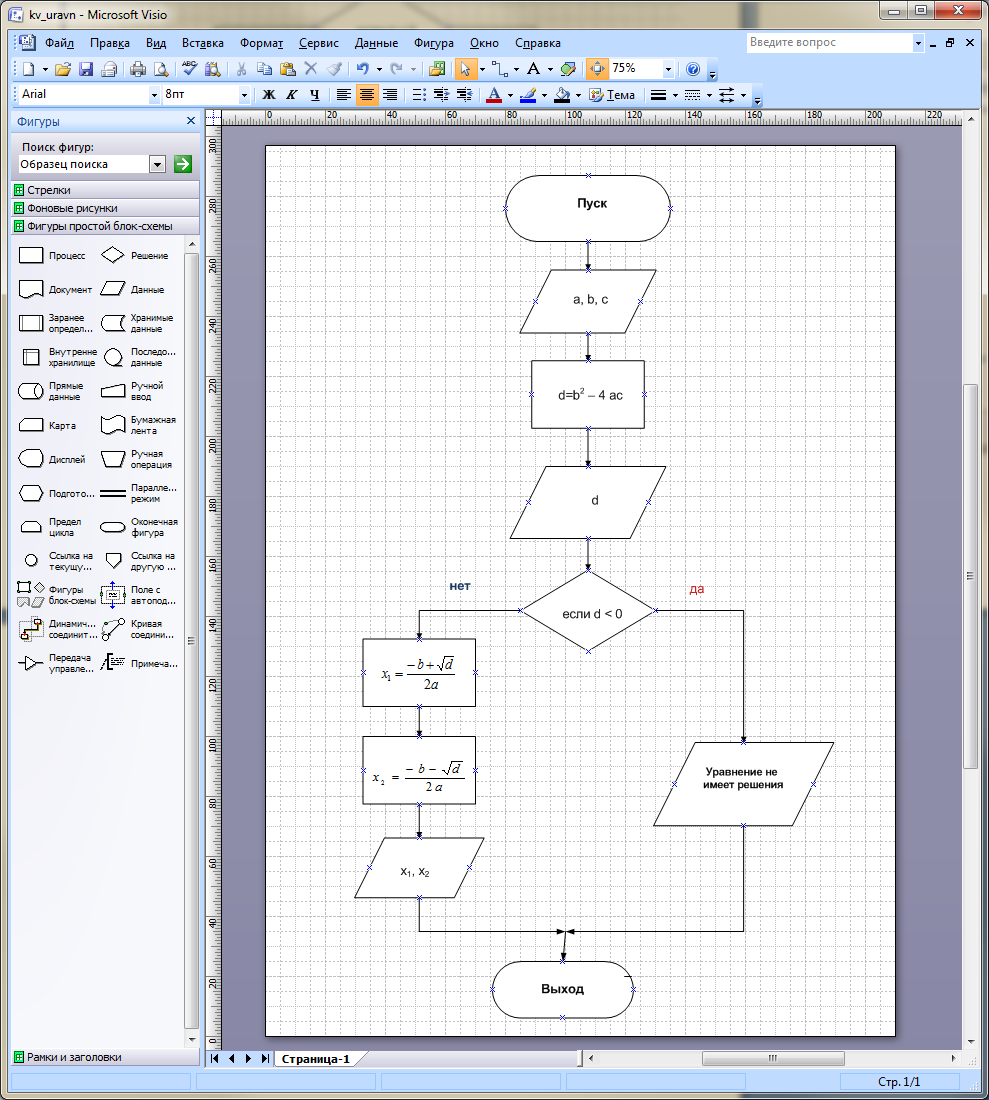
  1. Блок-схема решения квадратного уравнения имеет следующий вид:

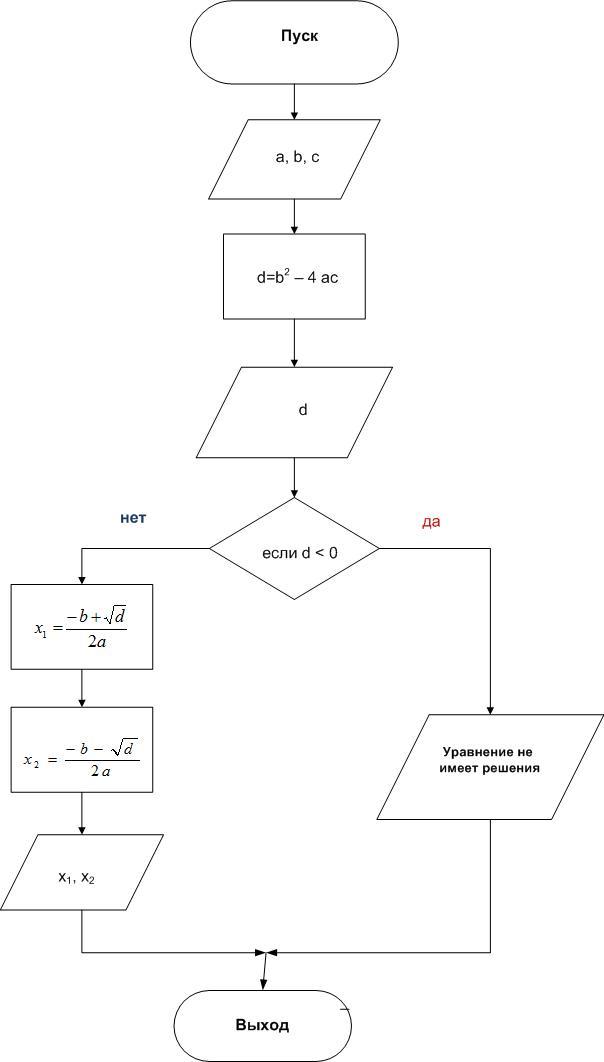
  1. Для создания данной блок-схемы необходимо перетащить мышью нужные фигуры на рабочую область документа и откорректировать их размеры.

Понадобятся следующие фигуры:

  • 2 «Оконечные фигуры» («Пуск» и «Выход»): ;
  • 3 фигуры «Процесс»: ;
  • 1 фигура «Решение»: ;
  • 4 фигуры «Данные»: .
  1. В результате действий рабочая область приобретёт следующий вид:

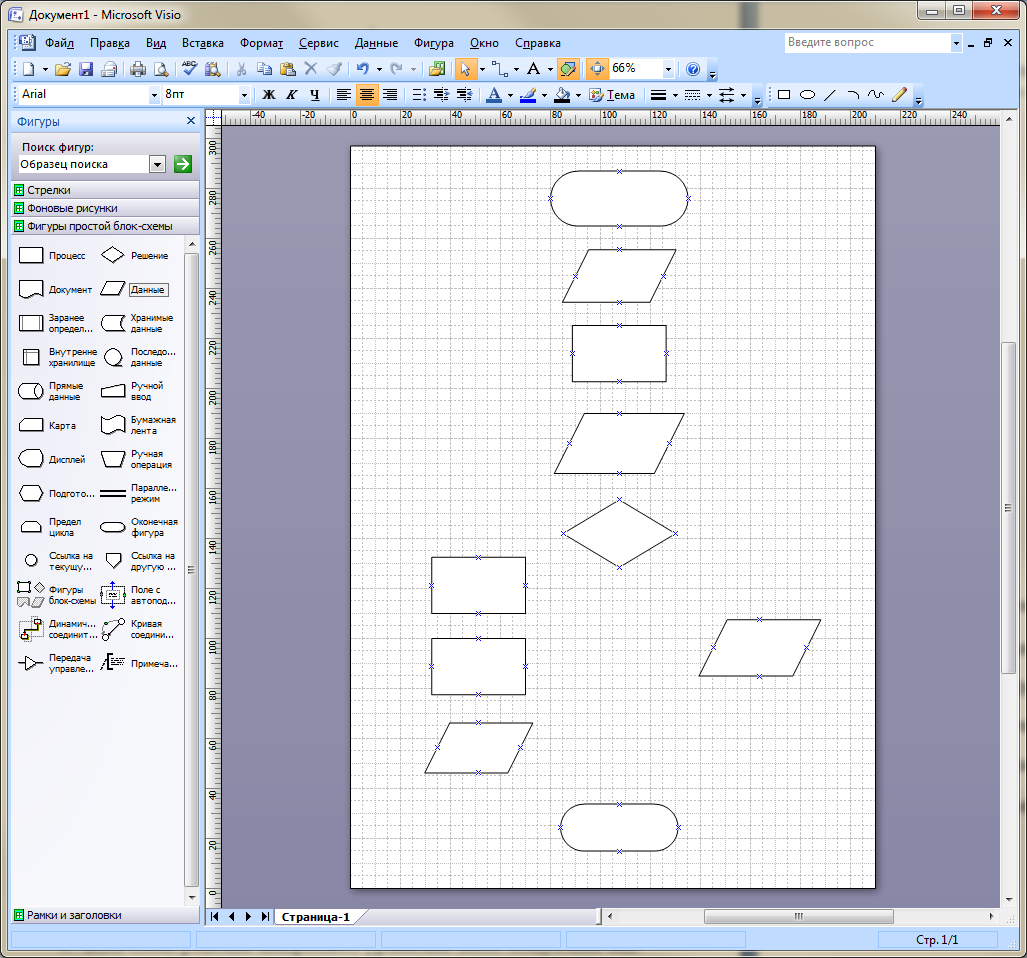
  1. На первую «Оконечную фигуру» необходимо добавить текст — «Пуск». Для этого необходимо выполнить следующие действия.
  • Выбрать на панели инструментов кнопку «Текст» :

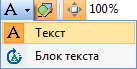
  • В появившейся рамке ввести с клавиатуры текст «Пуск»;

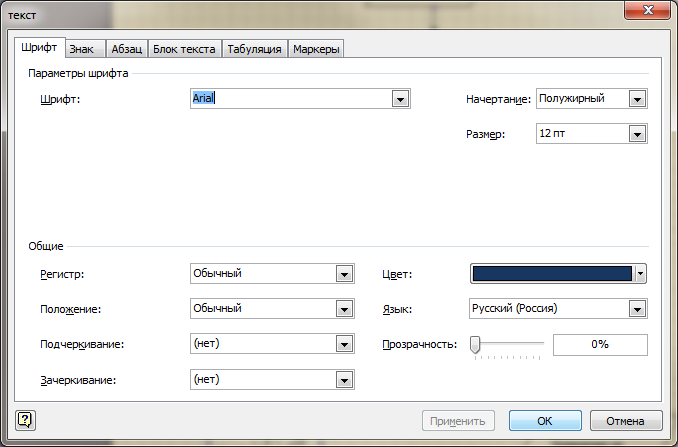
  • В меню выбрать команду «Формат», опцию «Текст и отформатировать текст: шрифт — Arial; размер — 12 пт; начертание — полужирный; цвет — черный;

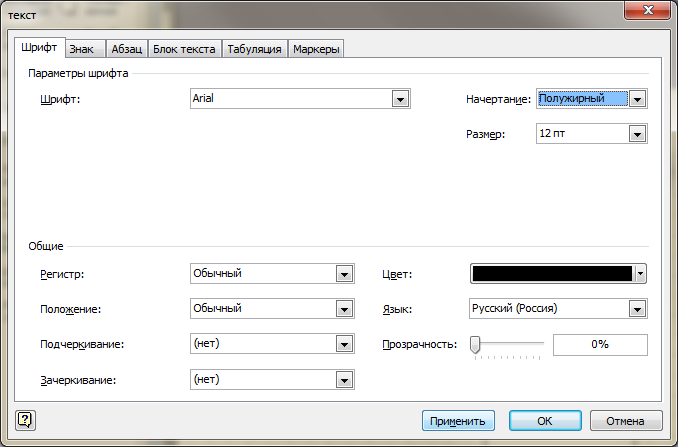
  • Нажать кнопки Применить и ОК.

  1. По аналогии добавить на остальные фигуры необходимый текст (цвет текста можно варьировать по желанию):
  • На первую фигуру «Данные»: a, b, c;
  • На первую фигуру «Процесс»: D = b 2 -4ac. Для написания верхнего индекса b 2 необходимо выбрать команду меню «Формат», опцию «Текст», положение — «Надстрочный»:

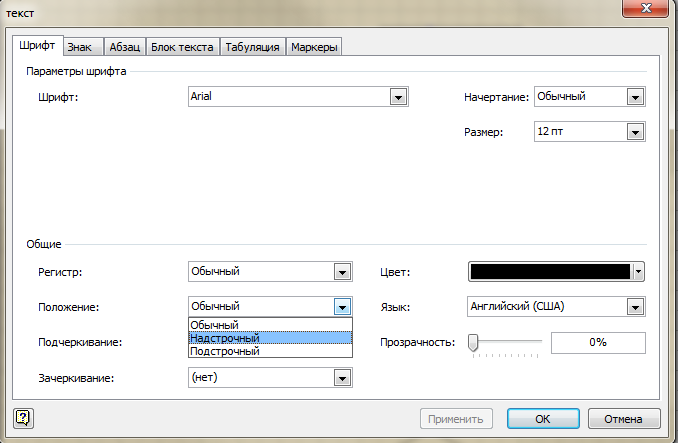
  • На вторую фигуру «Данные»: D;
  • На фигуру «Решение»: Если D < 0;

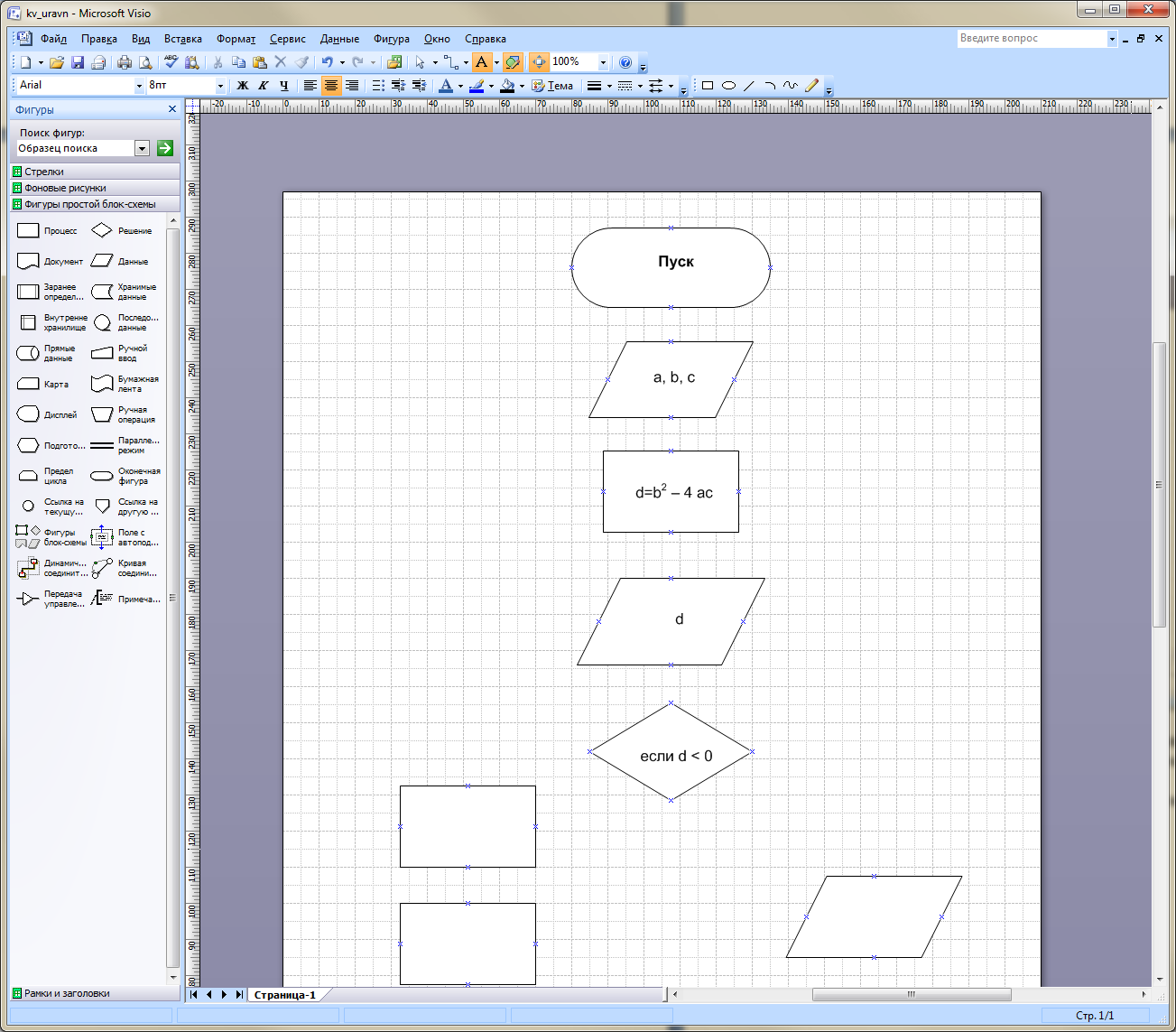
  • На третью фигуру «Данные»: x1, x2. Для написания нижних индексов x1, x2 необходимо выбрать команду меню «Формат», опцию «Текст», положение — «Подстрочный»
  • На четвертую фигуру «Данные»: «Уравнение не имеет решения»;
  • На вторую «Оконечную фигуру» необходимо добавить текст — «Выход»: шрифт — Arial; размер — 12 пт; начертание — полужирный; цвет — черный;

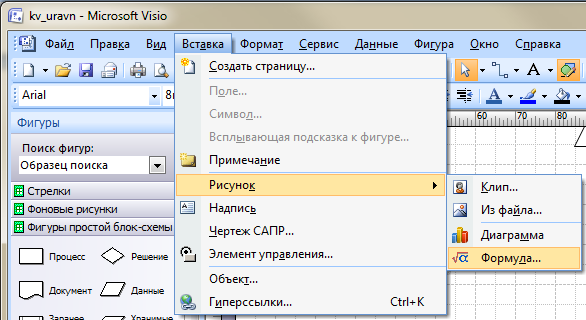
  • Для вставки формул необходимо выбрать команду меню «Вставка», «Рисунок», «Формула» (или «Вставка», «Объект», редактор формул «MS Equation 3.1»);

  • С помощью редактора формул MS Equation ввести формулу для расчета x1: ;

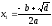  • Поместить формулу на вторую фигуру «Процесс»;
  • Скопировать формулу (команды «Копировать» и «Вставить») и изменить ее на ;
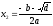  • Поместить формулу на третью фигуру «Процесс».

  1. При необходимости корректировки размеров фигуры необходимо выделить фигуру с помощью инструмента «Указатель» и произвести нужные действия.
  2. Добавить на блок-схему соединительные линии. Для этого необходимо выполнить следующие действия:
  • Выбрать на стандартной панели инструментов инструмент «Соединительная линия» (прямоугольная);
  • Провести между точками соединения фигур блок-схемы соединительные линии:

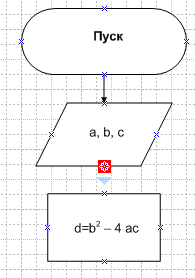
  • К фигуре «Решение» соединительные линии провести, отпуская и нажимая левую кнопку мыши:
Читайте также:
Как установить программу wi fi на компьютер

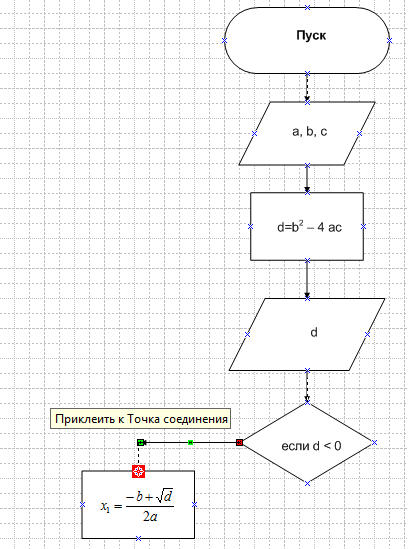
  • При необходимости изменения или форматирования соединительных линий целесообразно вызвать правой кнопкой мыши контекстное меню:

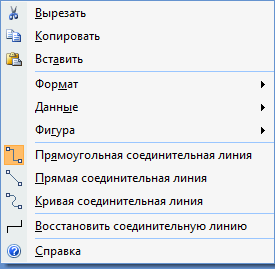и отформатировать соединительную линию с помощью диалогового окна: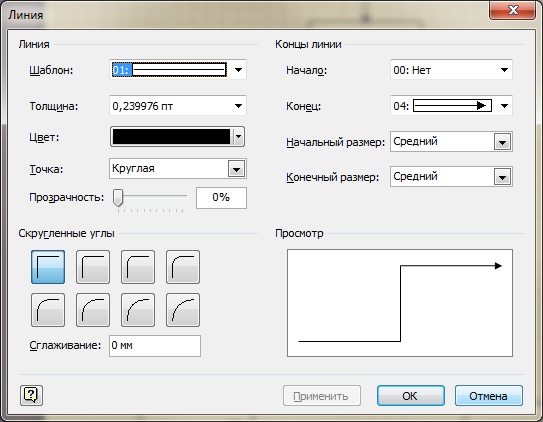

  • Внимание! При трудностях работы с «Соединительными линиями» можно добавить дополнительно на панель инструментов панель «Рисование» (если этой панели нет);
  • Панель добавляется командой меню «Вид», «Панели инструментов», «Рисование»:

  • Добавленная панель инструментов выглядит следующим образом:

  • Линии между фигурами можно провести мышью с помощью инструмента «Линия», выбрав типом конца линии стрелку:

  • Итоговая схема (с проведенными соединительными линиями ) выглядит следующим образом:

  1. Добавить к блоку решения надписи «да» и «нет» над линиями условия. Для этого необходимо выполнить следующие действия.
  • Выбрать команду меню «Вставка», «Надпись»;

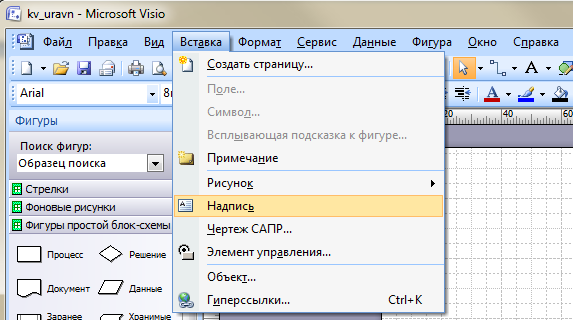
  • В появившейся рамке ввести слева от блока «Решение» с клавиатуры текст «нет» и отформатировать с помощью команды «Формат»: шрифт — Arial; размер — 12 пт; начертание — полужирный; цвет — темно-синий);

  • Справа от блока «Решение» с клавиатуры текст «да» и отформатировать с помощью команды «Формат»: шрифт — Arial; размер — 12 пт; начертание — полужирный; цвет — красный).

  1. Для подписи соединительных линий также можно щелкнуть двойным щелчком мыши по соединительной линии условия, в появившемся поле ввести текст «да» или «нет»

и затем отформатировать выделенный текст (по описанному выше образцу), вызвав правой кнопкой диалоговое окно «Текст»:

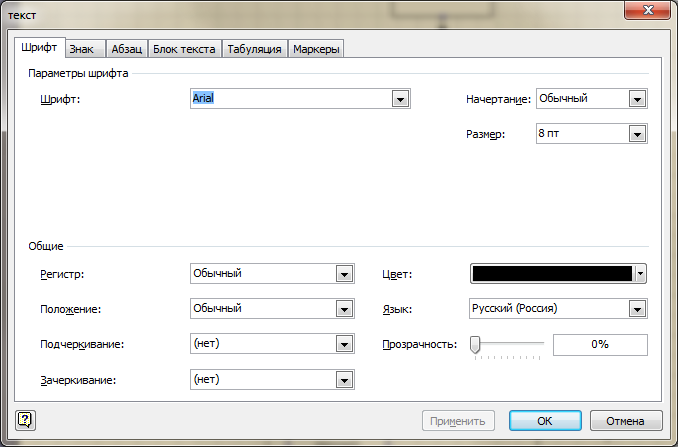
  1. Сгруппировать блок-схему в единый объект. Для этого необходимо выполнить следующие действия:
  • Щелкнуть на панели инструментов «Указатель» ;
  • Выделить мышью все фигуры до появления соответствующих маркеров;
  • Правой кнопкой мыши вызвать контекстное меню, команды «Фигура» и «Группировать»:

  1. Проверить и сохранить результаты работы, выбрав команду меню «Файл» и «Сохранить» (в папку «Мои документы»). Созданный файл назвать kv_uravn.vsd.

  1. Снова выбрав команду меню «Файл» и команду «Сохранить как» (в папку «Мои документы»). Выполнить трассировку (конвертацию) файла в формат jpeg (kv_uravn.jpg).

  1. Проверьте наличие двух файлов (разных типов!) в папке «Мои документы».

Источник: studfile.net

Решение квадратного уравнения: алгоритм и программа

Программирование на языке Python (§ 54 - § 61)

program QuadraticEquation;
var a, b, c, d, x1, x2: real;
begin
readln(a, b, c);
d := b * b — 4 * a * c;
d >= 0
begin
d <> 0
begin
x1 := (-b + sqrt(d)) / 2 * a;
x2 := (-b — sqrt(d)) / 2 * a;
writeln(‘x1 = ‘, x1:4:2, ‘, x2 = ‘, x2:4:2)
end
begin
x1 := -(b / 2 * a);
знаков перед
после запятой>
writeln(‘x = ‘, x1:4:2)
запятой>
end
end
writeln(‘No real solutions!’);
end.

8.

ax2+bx+c=0
a=0
уравнение линейное
a≠0

9. Специальные логические операции

Условие1 AND Условие2
ветка THEN, если выполняются оба условия
Условие1 OR Условие2
ветка THEN, если выполняется хотя бы одно
условие

10. Специальные логические операции

Условие1 XOR Условие2
ветка THEN, если ровно одно из двух условий
NOT — логическое НЕ (отрицание).

11. Оператор выбора CASE

case выражение of
значение1 : оператор ;
значение2 : оператор ;
.
значениеN : оператор
else оператор;
end;

12. Пример

Определить к какому кварталу относится месяц
Program Name;
var MONTH: integer;
begin
case MONTH of
1, 2, 3 : writeln (‘Первый квартал‘);
4, 5, 6 : writeln (‘Второй квартал‘);
7, 8, 9 : writeln (‘Третий квартал‘);
10, 11, 12 : writeln (‘Четвёртый квартал‘);
end;

13. Задания

1.Напишите программу, которая
определяет четное или не четное число.
2.Написать программу преобразования
цифр в слова.
3.Написать программу для нахождения
числа дней в месяце, если даны:
номер месяца n — целое число;
а, равное 1 для високосного года и равное
0 в противном случае.

Источник: ppt-online.org

Рейтинг
( Пока оценок нет )
Комментарии0
Загрузка ...
Похожие материалы
EFT-Soft.ru